MATLAB实验报告(猎狗追兔子的问题)

数学实验报告实验一：有一只猎狗在B 点位置发现了一只兔子在正东北方距离它200米的地方O 处，此时兔子开始以8米/秒的速度向正西北方距离为120米的洞口A 全速跑去，假设猎狗在追赶兔子的时候始终朝着兔子的方向全速奔跑，用计算机仿真法等多种方法完成下面的实验：(1) 问猎狗能追上兔子的最小速度是多少？(2) 在猎狗能追上兔子的情况下，猎狗跑过的路程是多少？ (3) 画出猎狗追赶兔子奔跑的曲线图。

分析：（1）建立新的坐标，将西北方向转变为新的Y 轴的正向，西南方向作为X 轴的负方向。

则猎狗的初始坐标为（-200，0），兔子初始坐标为（0，0），兔子的速度为a=8m/s ，则在时刻t ，兔子的坐标为（0，at ）,猎狗的坐标为（x,y ）,则有dx dta dxy d x -=22。

解得y=2c [r +11r c x +1）（_r -11r c x -1）（]+21r cr -，当x=0时，y=21r cr -，所以t=a y =22cb bc-,而算得时间t=15s ，故求得猎狗的速度的最大值b=16.85（m/s ）程序设计：c=-200;a=8;b=16.85;d=0.01;dt=2;t=0;gx=-100*sqrt(2);gy=-100*sqrt(2);tx=0;ty=0; while (sqrt((gx-tx)^2+(gy-ty)^2)>d) pause(0.000001) hold onaxis([-100*sqrt(2) 0 -100*sqrt(2) 60*sqrt(2)]); t=t+dt;gx=gx-b*dt*(a*t/sqrt(2)+gx)/sqrt((a*t/sqrt(2)+gx)^2+(a*t/sqrt(2)-gy)^2); gy=gy+b*dt*(a*t/sqrt(2)-gy)/sqrt((a*t/sqrt(2)+gx)^2+(a*t/sqrt(2)-gy)^2); tx=-a*t/sqrt(2); ty=a*t/sqrt(2);plot(gx,gy,'r.',tx,ty,'b*') end问题求解结果与结论：所以猎狗能追上兔子。

MATLAB实验报告电气14班张程21104011202012年4月12日星期四一．实验目的1.学会用MATLAB软件求解微分方程的初值问题。

2.学会根据实际问题建立简单微分方程数学模型。

3.了解级计算机数据仿真、数据模拟的基本方法。

二．实验题目有一只猎狗在B处发现了一只兔子在正东北方距离它200米的地方O处，此时兔子开始以8米每秒的速度向正西北方向距离为120米的洞口A全速跑去，假设猎狗在追赶兔子时始终朝着兔子的方向全速奔跑。

（1）问猎狗能追上兔子的最小速度是多少？（2）选取猎狗的速度分别为15、18米每秒，计算猎狗追上兔子是所跑过的路程和所用的时间。

（3）画出猎狗追赶兔子奔跑的曲线图。

三．实验过程（1）将所有路径转化入第一象限，从而转化为教材中缉私艇和走私船的问题。

兔子起始位置为（0，0），奔跑方向为Y轴正方向，猎狗起始位置为（200，0）。

兔子刚好被追上时跑的距离Y=CR/1-R²。

（R为兔子与猎狗速度之比）时间T=CR/A(1-R²)=BC/(B²-A²)。

当兔子进洞的时候刚好被追到，这种情况下猎狗所需速度最小。

将C=200,Y=120带入方程并利用MATLAB求解：所以最小速度为17.08m/s。

(2)程序如下：运行结果：t =18.2000 s =273.0000将程序中b改为18运行结果为：t =13.6000 s =244.8000 兔子跑过距离分别为145.6000、108.8000，所以第一次兔子已经进洞，猎狗追不上。

（3）下图分别为猎狗速度为18m/s、15m/s时的模拟图。

四．反思总结1.实际问题的解决可以通过matlab等工具进行很好地计算和模拟，关键在于找到适当的方法。

2.实验过程中总会有这样或者那样的错误，在不断的更正中发现对程序的了解更深了一步。

3.同一个问题可以有多个解答方法，只要擅于分析和发现，在不断的总结中就可以有所收获。

1、猎狗前面26步远有一只野兔，猎狗追之. 兔跑8步的时间狗跑5步，兔跑9步的距离等于狗跑4步的距离.问：兔跑多少步后被猎狗抓获?此时猎狗跑了多少步?【解析】“猎狗前面26步”，显然指的是猎狗的26步，兔跑8步的时间狗跑5步，兔跑9步的距离等于狗跑4步的距离，可以统一为兔子跑72步的时间狗跑45步，兔子跑72步的距离狗跑32步距离，所以在兔子跑72步的时间里，狗比兔子多跑了45-32=13（步）的路程，这个13步是猎狗的13步，因此，要追上距离26（狗）步的距离，兔子跑了72×（26÷13）=144（步），此时猎狗跑了5×（144÷8）=90（步）【答案】兔子144步，猎狗90步。

2、猎人带猎狗去捕猎，发现兔子刚跑出40米，猎狗去追兔子。

已知猎狗跑2步的时间兔子跑3步，猎狗跑4步的距离与兔子跑7步的距离相等，求兔子再跑多远，猎狗可以追上它？【解析】设狗跑2步的时间为1(分钟)，兔跑3步的时间也为1(分钟)；再设狗的步长为7(米)，则兔的步长为4(米)，推出狗的速度是2×7=14，兔的速度是3×4=12。

用40÷（14－12）=20，20为追击时间。

再用兔的速度乘上追击时间可得兔跑的路程，即12×20=240（米）【答案】240米3、一只猎狗发现在离它18米远的前方有一只狐狸在跑，马上紧追上去，猎狗跑2步的路程狐狸需跑3步，若猎狗跑5步的时间，狐狸可跑7步，猎狗跑多少米能追上狐狸？【解析】设猎狗一步距离为A,狐狸一步则为(2/3)A 设单位时间X作为参数,在X时间内猎狗可以跑一步,则狐狸可以跑7/5步即在相同的X时间内,猎狗跑A,狐狸可跑(2/3)*(7/5)A=(14/15)A 时间相同,猎狗和狐狸的速度即为路程比,15:14 猎狗每跑15米,狐狸跑14米,可追上狐狸1米,所以猎狗要跑15*18=270米因为不知道到这是小学竞赛题还是中学题,所以用小学的方式解的,中学物理题的话,用公式V=S/T表示上面的东西就可以了,最后的速度V用参数表示出来4、一条猎狗追30米外的一只狐狸，狗跳跃一次为2米，狐狸跳跃一次为1米，而狐狸跳3次的时间，猎狗只能跳两次，猎狗跑多少米才能追上狐狸？【解析】分析：狐狸跳3次的时间，猎狗只能跳两次，也就是狐狸前进1×3＝3米，猎狗可以前进2×2＝4米，由于4－3＝1，所以猎狗每跑4米就追上狐狸1米，于是猎狗追上狐狸的需要跑4×30＝120（米）.5、一只野兔逃出85步后猎狗才追它，野兔跑8步的路程猎狗才需要跑3步，猎狗跑4步的时间野兔能跑9步，问猎狗需要跑多少步才能追上野兔？【解析】猎狗每跑12步这段时间内野兔跑27步而猎狗每跑12步的路程需要野兔跑32步所以猎狗每跑12步就可以比野兔多跑5步85÷5×12=204答：猎狗至少要跑204步才能追上野兔6、猎狗追赶前方30米处的野兔。

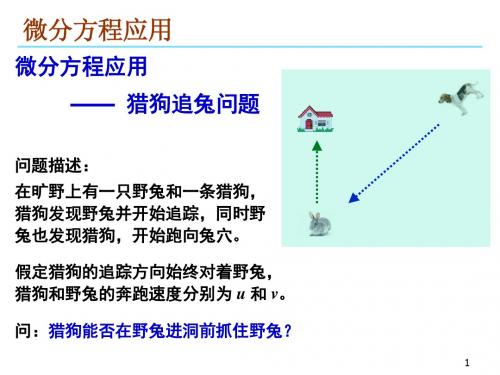
Matlab上机实验报告一．题目如图所示，有一只猎狗在B点位置发现了已知兔子在正东北方向距离它200米的地方O处，此时兔子开始以8米/秒的速度向正西北方向距离为120米的洞口全速跑去，假设猎狗在追赶兔子的时候始终朝着兔子的方向全速奔跑按要去完成以下的实验：（1）问猎狗能追上兔子的最小速度是多少？（2）选取猎狗的速度分别为15、18米/秒，计算猎狗追上兔子时跑过的路程和时间。

（3）画出猎狗追赶兔子奔跑的曲线图。

二．问题分析（1）本题目是在限定条件下求极值的问题，可以通过建立有约束条件的微分方程加以模拟。

（2）通过运用欧拉公式及改进欧拉公式的原理，结合高等数学的有关知识，对微分方程进行求解。

（3）将数学求解用Matlab程序语言进行实现，得出方程的近似解。

（4）最后解方程的解结合实际问题转化为具体问题的实际结果。

三．假设约定（1）假设在兔子和猎狗的运动过程中，两者的速度保持恒定，且不受其他因素的影响。

（2）假设在较短的时间内猎狗运动的轨迹为直线。

（3）当猎狗与兔子之间的距离相当小时，认为猎狗已经追上了兔子。

四．模型建立以BO所在的直线为x轴，以OA所在的直线为y轴建立如图所示的直角坐标系，则O点坐标（0，0），B点坐标（-200，0），A点坐标（0，120），设猎狗跑够的路程为s，经历的时间为t。

从猎狗发现兔子时起，在t时刻，兔子到达C(0，8t)点，猎狗到达(x,y)点，设猎狗的速度为v，由题意可知：dy/dx=(y-8t)/ads/dt=b对两边关于x求导可得：x*d2y=-a(dt/dx)dt/dx=-1/b*(1+(dy/dx)^2)^0.5于是：x*d2=8/v*(1+(dy/dx)^2)^0.5y(-200)=0,dy(-200)=0则该问题的模型建立五．模型求解1.方程求解令p=dy/dx，则d2y=dp/dx，所以方程可以化为：dp/(1+p^2)^0.5=8/v*dx/x⇨p+(1+p^2)^0.5=(x/-200)^(8/v)⇨p+(1+p^2)^0.5=-(-200/x)^(8/v)所以：dy/dx=0.5*((x/-200)^(8/v)- (-200/x)^(8/v))由高等数学的知识可以解得：y=-100*(-1/200*x)^(8/v+1)/(8/v+1)-100*(-1/200*x)^(-8/v+1)/(-8/v+1)+1600*v/(-64+v^2)2.最小速度令x=0，此时猎狗追上兔子，则兔子走过的距离为y=1600*v/(-64+v^2)则追赶的时间为：t=y/8=200*v/(-64+v^2)由于兔子跑回窝的时间是一个定植，所以当猎狗以最小速度追赶上兔子时，所经历的时间恰好为兔子跑回窝所需要的时间，即：200*v/(-64+v^2)=15可以解得：v=17.0803即猎狗的最小速度为17.0803米/秒3.变换速度1.当猎狗的速度为15米/秒时，由以上的分析可以知道猎狗不能追上兔子。

MATLAB R2014a 基础教程———MATLAB R2014a 快易行（上）前言MATLAB与Mathematica、Maple并称为“3M”，是数学界中三大著名软件，这些软件在数据运算处理上十分强大，备受科研工作者的青睐。

同时，MATLAB与Origin也是常见的绘图工具，MATLAB 侧重于图像的计算，Origin侧重于图像的表达。

另外，在仿真模拟方面，MATLAB与SYNESS、COMSOL等在该领域内被大家所推崇。

由此可见，MATLAB是一款功能强大、应用丰富且被广泛认可的科研工具，熟练掌握它有助于提高我们的科研质量。

在此之前，我做过关于Origin 9.0的“快易行”基础教程，思路是先把握软件的大体脉络，再根据自己的需求学习到边边角角。

可是，MATLAB却不能这样学，为什么呢？解压后的MATLAB R2014a有8.78G之大，而Origin 9.0只有663M，所以即使我们第一步只学主线，也会耗费巨大的时间与精力。

同时，学习跨度的增加很容易致使前面学了、后面忘了的尴尬局面，最后导致效果打折，如同古代打战时，切忌粮草供应线过长。

所以，在这款软件的学习上，希望大家能够有一条明确的思路，你要用MATLAB做什么，那我们就学什么，想多学点不是坏事，但猴子摘玉米的故事也是一个警钟。

好了，基于此思路，我们暂时就以MATLAB解决实际问题，计算微分方程并绘制相应图像为例，一步一步地进行学习。

这是以前写的一段话，这里同样受用：长话短说，学一款软件有两种方法，一种是拿着“从入门到精通”这类的书慢慢啃，啃完了就精通了，但除了高数我一点一点地啃完，其它的都没成功过。

另一种是先入门，几分钟或者个把小时内学会主线，剩下的再慢慢来，没必要全都会，根据自己的需求再学。

所以当时就想到了“快易行”这个概念：快速、容易、行得通。

讲重点，好上手，实用，复杂点的部分自己再慢慢来，这是本文的宗旨，也希望能达到这样的效果。

《数学建模》(2014春)课程期末论文摘要（一）对于问题一：自然科学中存在许多变量，也有许多常量，而我们要善于通过建立合适的模型找到这些变量之中的不变量。

猎狗追赶兔子的问题是我们在生活中常见的实例，而题目把我们生活中的普通的例子抽象成为高等数学中微分方程的例子，通过对高阶微分方程的分析，建立微分方程模型，并用数学软件编写程序求解，得出结论，解决生活中常见的实际问题。

（二）对于问题二：学习使用matlab进行数学模型的求解，掌握常用计算机软件的使用方法。

关键词微分方程导数的几何意义猎狗追兔子数学建模数学软件一、问题重述如图1所示，有一只猎狗在B 点位置，发现了一只兔子在正东北方距离它250m 的地方O 处，此时兔子开始以8m/s 的速度正向正西北方向，距离为150m 的洞口A 全速跑去. 假设猎狗在追赶兔子的时候，始终朝着兔子的方向全速奔跑。

请回答下面的问题：⑴ 猎狗能追上兔子的最小速度是多少？ ⑵ 在猎狗能追上兔子的情况下，猎狗跑过的路程 是少？⑶ 假设猎狗在追赶过程中，当猎狗与兔子之间的距离为30m 时，兔子由于害怕导致奔跑速度每秒减半， 而狗却由于兴奋奔跑速度每秒增加0.1倍，在这种情 况下回答前面两个问题。

二、问题分析与假设在猎狗追赶兔子的时候猎狗一直朝着兔子的方向追赶，所以可以建立平面直角坐标系，通过导数联立起猎狗运动位移，速度和兔子的运动状态。

1.假设兔子的运动是匀速的。

2.假设猎狗的运动轨迹是一条光滑并且一阶导数存在的曲线。

3.猎狗的运动时匀速或者匀变速的。

4.猎狗运动时总是朝向兔子。

三、模型的建立及求解3.1 符号规定1.（x ，y ）：猎狗或者兔子所在位置的坐标。

2. t ：从开始到问题结束经过的时间。

3. a:猎狗奔跑的路程。

4. v:猎狗的奔跑速度。

3.2 模型一的建立与求解猎狗能够抓到兔子的必要条件：猎狗的运动轨迹在OA 要有交点以OA 为y 轴，以OB 为x 轴建立坐标系，则由图有O(0，0)，A(0,150),B(250，0)，兔子的初始位置0点,而猎狗初始位置是B 点，t （s ）后猎狗到达了C （x ，y ），而兔子到达了D （0，8t ），则有CD 的连线是猎狗运动轨迹的一条切线，由导数的几何意义有：BA N OW S E BANO W SE8dy y tdx x-=dav dt=da =三式联立消去t ，得到;设：若猎狗可以追上兔子则有当兔子在OA,猎狗在OB 之间运动时此方程有解，设：得到：得到：228d y x dx v =8q v=dyp dx =22d y dp dxdx=dpdxq x =(250)0p=()250qx p +=250()qp x -=-两式联立相加得到：1.如果q=1即v=8 m/s 得到所以此情况无交点，所以v=8m/s 猎狗无法追上兔子； 2.如果q<1即v>8m/s 得到此情况有交点，所以有可能能够追上兔子，如果要追上兔子需要y<=150;解得到： 即所以这种情况下能够追上的最小速度是 .3.如果q>1 利用上式得到，所以这种情况不能追上兔子。

数学实验报告—猎狗追赶兔子模型实验一.实验问题有一只猎狗在B点位置发现了一只兔子在正东北方距离它200米的地方O处，此时兔子开始以8米/秒的速度向正西北方距离为120米的洞口A全速跑去，假设猎狗在追赶兔子的时候始终朝着兔子的方向全速奔跑，用计算机仿真法等多种方法完成下面的实验：(1) 问猎狗能追上兔子的最小速度是多少？(2) 在猎狗能追上兔子的情况下，猎狗跑过的路程是多少？(3) 画出猎狗追赶兔子奔跑的曲线图。

(4) 假设在追赶过程中，当猎狗与兔子之间的距离为30米时，兔子由于害怕,奔跑的速度每秒减半，而猎狗却由于兴奋奔跑的速度每秒增加0.1倍，在这种情况下，再按前面的（1）—（3）完成实验任务。

一．问题的分析模型求解（1）求解析解有方程：{√1+p2=r dxx,p(c)=0解该变量分离方程得p+√1+p2=(xc)r, 等价地亦可转换为P -√1+p 2=−(c x )r从而可得{dy dx =12[(x c )r −(c x )r ]y (c )=01)当r<1时，方程的解为y =c 2[11+r (x c )r −11−r (c x )1−r ]+cr 1−r 2, 此为猎狗追赶兔子的路线函数。

当x=0时，猎狗追上兔子，猎狗走过的距离为 y =cr 1−r 2,追赶时间为t =y a =cr a(1−r 2)=bc(b 2−a 2).2）当r=1时，方程的解为Y=12(x 2−c 22c −c ln x c ),3）当 r>1时，方程的解为 y =c 2[11+r (x c )1+r +1r−1(c x )r−1]−cr r 2−1, (2)用MATLAB 软件求解析解在MATLAB 软件命令窗中执行命令Dsolve(‘Dy=1/2*((x/c)^r-(c/x)^r)’,’y(c)=0’,’x ’)得方程的解析解为ans=1/2*exp(-r*(log(c)-log(x)))*c^r*(1/c)^r/(r+1)*x+1/2*exp(r*(log(c)-log(x)))/((-1+r)*x-1/2*c*(-(1/c)^r*c^r+c^r*(1/c)^r*r+r+1)/(r^2-1)(3)用MATLAB 软件求数值解先生成初值问题的函数文件。