第一章_透视的基本概念
- 格式:ppt
- 大小:9.52 MB
- 文档页数:58




透视是绘画理论术语,指在平面上描绘物体的空间关系的方法或技术。
最初研究透视是采取通过一块透明的平面去看景物的方法,将所见景物准确描画在这块平面上,即成该景物的透视图。
后遂将在平面上根据一定原理,用线条来显示物体的空间位置、轮廓和投影的科学称为透视学。
在画者和被画物体之间假想一面玻璃,固定住眼睛的位置(用一只眼睛看),连接物体的关键点与眼睛形成视线,在相交于假想的玻璃,在玻璃上呈现的各个点的位置就是要画的三维物体在二维平面上的点的位置。
透视有若干基本规律,例如“近大远小,近高远低,近宽远窄,近实远虚”等。
这些基本规律决定了物体在不同角度和距离观察时呈现的视觉效果。
掌握透视的基本规律对于绘画、设计、建筑等领域至关重要,能够帮助艺术家和设计师创造出更加真实、立体和有层次感的作品。



透视的基本概念主讲:马宗仁学校:甘肃省靖远师范学校一、透视和透视学1、透视“透视”的英文perspective,来自拉丁文Perspicere,透而视之,其含义为透视感、透视画法、透视效果、透视图。
2、透视学眼睛通过一块假想的透明平面来观察对象,并借此研究在一定视觉空间范围内,物体图形产生原理、变化规律,以及作图方法的一门学科。
透视学是通过平面上的形来表现空间感和立体感,即研究在平面上立体造型的规律,所以又叫做几何透视或线透视。
学习透视学的目的一、掌握在二维平面上表现三维景物的画法;二、用它的规律来指导我们认识事物,以便更有效地观察和记忆物体的形象,准确而艺术的表现物象,表达作者的创作意图。
第一节概述——透视学发展简况1、文艺复兴前——萌芽期原始时期古埃及时期古希腊时期古罗马时期中世纪2、文艺复兴时期透视开始以一门独立学科出现,是透视学的发展期。
14世纪的代表人物:乔托15世纪的代表人物:布鲁内莱斯奇、弗兰西斯卡、阿尔贝蒂、达·芬奇、乌切洛、马萨乔3、17-18世纪经历文艺复兴时期后,各种透视规则及画法以完备,透视学开始进入成熟期。
17世纪的代表人物:沙葛、波佐18世纪的代表人物:布鲁克·泰勒、盖斯帕尔·蒙诺;普桑、华托、马尼亚斯科等。
4、19-20世纪传统意义上的透视学进一步被消弱,取而代之的是大量组合透视、无透视、变形透视、幻觉透视等主观意识以及意象化的空间表现。
代表人物:杜尚、毕加索、埃舍尔等。
第二节透视图形的产生及特征一、透视图形的产生人观察客观存在的景物,是由于光线照射到的物体后,物体把光线反射到人们眼内视网膜上而产生的结果。
如果我们站在不动的窗玻璃前,固定视点,把透过玻璃所看到的物象依样描绘在窗玻璃上,描绘出的图像就是一幅存在着透视现象的透视图。
第三节透视基本术语视角:任意两条边缘视线与视点所成的夹角。
视锥:汇聚在眼睛瞳孔内的无数视线形成的圆锥。
视锥的中轴线称为视心线,它表示画者注视的方向。

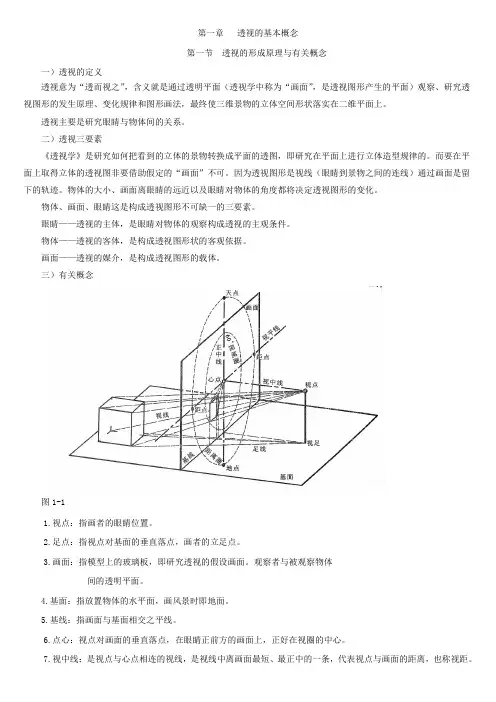
第一章透视的基本概念第一节透视的形成原理与有关概念一)透视的定义透视意为“透而视之”,含义就是通过透明平面(透视学中称为“画面”,是透视图形产生的平面)观察、研究透视图形的发生原理、变化规律和图形画法,最终使三维景物的立体空间形状落实在二维平面上。
透视主要是研究眼睛与物体间的关系。
二)透视三要素《透视学》是研究如何把看到的立体的景物转换成平面的透图,即研究在平面上进行立体造型规律的。
而要在平面上取得立体的透视图非要借助假定的“画面”不可。
因为透视图形是视线(眼睛到景物之间的连线)通过画面是留下的轨迹。
物体的大小、画面离眼睛的远近以及眼睛对物体的角度都将决定透视图形的变化。
物体、画面、眼睛这是构成透视图形不可缺一的三要素。
眼睛——透视的主体,是眼睛对物体的观察构成透视的主观条件。
物体——透视的客体,是构成透视图形状的客观依据。
画面——透视的媒介,是构成透视图形的载体。
三)有关概念图1-11.视点:指画者的眼睛位置。
2.足点:指视点对基面的垂直落点,画者的立足点。
3.画面:指模型上的玻璃板,即研究透视的假设画面。
观察者与被观察物体间的透明平面。
4.基面:指放置物体的水平面,画风景时即地面。
5.基线:指画面与基面相交之平线。
6.点心:视点对画面的垂直落点,在眼睛正前方的画面上,正好在视圈的中心。
7.视中线:是视点与心点相连的视线,是视线中离画面最短、最正中的一条,代表视点与画面的距离,也称视距。
8.视平线:画面上过心点的水平线,平视时与地平线重合,代表视点的位置高度,是上下分割画面的基准线。
9、正中线:过心点的垂直线,是左右分割画面的基准线。
10、距点:将视距分别标在心点两侧的视平线上,所得两点就是距点。
11、距离圈:在画面上,一心点为圆心,以视距为半径所画的视域圈。
12、天点:距离圈与正中线在视平线上方相交的点,到心点的距离也等于视距。
13、地点:距离圈与正中线在视平线下方相交的点,到心点的距离也等于视距。


基础美术详细教案(透视)第一章:透视基础1.1 透视的定义和作用解释透视是一种表现空间深度的绘画技巧强调透视在美术创作中的重要性1.2 透视的基本原理介绍平行透视和成角透视的概念解释一点透视和两点透视的差异1.3 透视图形的绘制步骤演示如何绘制一个简单的透视图形指导学生通过观察和测量来绘制透视图形第二章:一点透视2.1 一点透视的原理解释一点透视的特点和应用场景强调一点透视的简洁性和效果2.2 一点透视的绘制方法演示如何运用一点透视绘制图形指导学生通过一点透视绘制自己的作品2.3 一点透视的实际应用提供一些一点透视的实例作品供学生参考鼓励学生创作自己的一点透视作品第三章:两点透视3.1 两点透视的原理解释两点透视的特点和应用场景强调两点透视的复杂性和效果3.2 两点透视的绘制方法演示如何运用两点透视绘制图形指导学生通过两点透视绘制自己的作品3.3 两点透视的实际应用提供一些两点透视的实例作品供学生参考鼓励学生创作自己的两点透视作品第四章:空间感和深度感的表现4.1 空间感和深度感的概念解释空间感和深度感在透视中的重要性强调透视对空间感和深度感的表现作用4.2 空间感和深度感的绘制方法演示如何通过透视表现空间感和深度感指导学生通过透视表现自己的作品中的空间感和深度感4.3 空间感和深度感的实际应用提供一些空间感和深度感的实例作品供学生参考鼓励学生创作自己在作品中表现空间感和深度感的作品第五章:透视在实际作品中的应用5.1 透视在风景画中的应用解释透视在风景画中的重要作用强调透视在表现风景画中的空间感和深度感5.2 透视在静物画中的应用解释透视在静物画中的重要作用强调透视在表现静物画中的空间感和深度感5.3 透视在人物画中的应用解释透视在人物画中的重要作用强调透视在表现人物画中的空间感和深度感第六章:透视中的物体比例与形态6.1 透视对物体比例的影响解释在透视中物体比例如何随着远近变化强调掌握透视中物体比例的重要性6.2 透视中物体的形态变化介绍透视中物体形态如何随着视角变化指导学生如何绘制透视中的物体形态6.3 实践练习:透视中的物体比例与形态提供练习题,让学生在给定的透视图中填充物体检查学生的作品,提供反馈和建议第七章:建筑透视7.1 建筑透视的基本原理解释建筑透视的概念和作用强调建筑透视在建筑设计中的重要性7.2 建筑透视的绘制方法演示如何绘制建筑透视图指导学生通过建筑透视绘制自己的作品7.3 建筑透视的实际应用提供一些建筑透视的实例作品供学生参考鼓励学生创作自己的建筑透视作品第八章:透视中的光影处理8.1 透视中光影的作用解释光影在透视中的重要性强调光影处理对透视作品的影响8.2 透视中光影的绘制方法演示如何通过透视处理光影指导学生通过透视处理自己的作品中的光影8.3 实践练习:透视中的光影处理提供练习题,让学生在给定的透视图中添加光影检查学生的作品,提供反馈和建议第九章:透视作品的评价与分析9.1 透视作品的评价标准介绍评价透视作品的方法和标准强调评价透视作品的重要性9.2 透视作品的分析方法介绍分析透视作品的方法和技巧指导学生如何分析透视作品9.3 实践练习:透视作品的评价与分析提供一些透视作品供学生评价和分析检查学生的评价和分析结果,提供反馈和建议第十章:拓展透视技巧与应用10.1 透视的变形与夸张解释在透视中如何运用变形与夸张强调变形与夸张在透视作品中的效果10.2 透视与其他绘画技巧的结合介绍如何将透视与其他绘画技巧结合指导学生如何运用透视与其他绘画技巧创作作品10.3 透视在创新作品中的应用提供一些创新透视作品的实例供学生参考鼓励学生运用透视创作创新作品重点和难点解析1. 透视的基本原理:理解透视的概念和作用,以及透视的基本原理,如平行透视和成角透视,是一点透视和两点透视的基础。
透视的基本概念1、什么是透视透视是造型艺术所依赖的一门科学。
透视也是一种视觉现象。
这种视觉现象是随着人的视点移动而产生变化,即这种变化与视点的位置和距离是分不开的。
在现实生活中,当人们边走边看景物时,景物的形状会随着脚步的移动在视网膜上不断地发生变化,因此对某个物体很难说出它固定的形状。
观者只有停住脚步,眼睛固定朝一个方向看去时,才能描述某个景物在特定位置的准确形状。
再则,随着景物与我们远近距离不同,所看到的景物形状也不一样。
通常在距离的前提下,空间越深,透视越大。
同样大小的物体,也会因视点与物体远近距离的不同而产生大小变化。
这就是我们通常所讲的近大远小透视变化规律。
例如,当我们站在路中间就会发现,越近的树、灯越高越大,越远的树、灯越矮越小。
“透视”一词来自拉丁文“persdicere”,意为“透而视之”。
在画者和景物之间竖立一块透明玻璃的平面上,即可得到物体的透视图形,使二维空间纸上呈现出三维立体空间。
由此可得出透视的含义:通过透明平面观察,确定透视图形的发生原理、变化规律和图形画法。
2、透视的特点透视是一种绘画与艺术设计活动中观察方法和研究画面空间的重要手段。
运用物体形状近大远小、物体明暗对比的近强远弱、物体的色彩近纯远灰等规律,可以归纳出视觉空间变化的规律,可以使平面景物图形产生距离感和立体凹凸感。
所以说透视最显著的特点就是在二维空间的平面上形成视觉三维立体空间。
3、透视的分类透视的分类,我们从以下几个方面进行分析。
(1)从理论研究角度分类线透视:它是使观者识别画面空间距离最为有效的表现方法。
场景中的远伸平行线,看去愈远愈聚拢,直至会合于一点。
色彩透视:近处色彩偏暖,远处色彩偏冷。
这是大气层的阻隔而产生的变化。
如:近处物体色彩倾向鲜明,接近固有色,带有黄橙色调。
远处色调倾向暗淡灰紫,深色物体则偏蓝灰色。
消逝透视:物体的明暗对比和清晰度随着距离的变化而产生强弱变化。
如近处物体明暗对比强烈,有较清晰的视觉轮廓;远处物体明暗对比弱,细节和轮廓都较模糊,甚至混为一片。