下载文档原格式
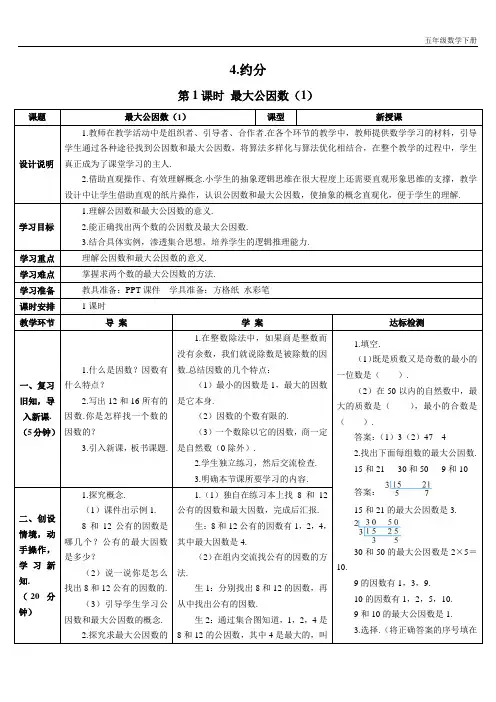
4.约分第1课时最大公因数（1）课题最大公因数（1）课型新授课设计说明1.教师在教学活动中是组织者、引导者、合作者.在各个环节的教学中，教师提供数学学习的材料，引导学生通过各种途径找到公因数和最大公因数，将算法多样化与算法优化相结合，在整个教学的过程中，学生真正成为了课堂学习的主人.2.借助直观操作、有效理解概念.小学生的抽象逻辑思维在很大程度上还需要直观形象思维的支撑，教学设计中让学生借助直观的纸片操作，认识公因数和最大公因数，使抽象的概念直观化，便于学生的理解.学习目标1.理解公因数和最大公因数的意义.2.能正确找出两个数的公因数及最大公因数.3.结合具体实例，渗透集合思想，培养学生的逻辑推理能力.学习重点理解公因数和最大公因数的意义.学习难点掌握求两个数的最大公因数的方法.学习准备教具准备：PPT课件学具准备：方格纸水彩笔课时安排1课时教学环节导案学案达标检测一、复习旧知，导入新课.（5分钟）1.什么是因数？因数有什么特点？2.写出12和16所有的因数.你是怎样找一个数的因数的？3.引入新课，板书课题.1.在整数除法中，如果商是整数而没有余数，我们就说除数是被除数的因数.总结因数的几个特点：（1）最小的因数是1，最大的因数是它本身.（2）因数的个数有限的.（3）一个数除以它的因数，商一定是自然数（0除外）.2.学生独立练习，然后交流检查.3.明确本节课所要学习的内容.1.填空.（1）既是质数又是奇数的最小的一位数是（）.（2）在50以内的自然数中，最大的质数是（），最小的合数是（）.答案：（1）3（2）47 42.找出下面每组数的最大公因数.15和21 30和50 9和10答案：15和21的最大公因数是3.30和50的最大公因数是2×5＝10.9的因数有1，3，9.10的因数有1，2，5，10.9和10的最大公因数是1.3.选择.（将正确答案的序号填在二、创设情境，动手操作，学习新知.（20分钟）1.探究概念.（1）课件出示例1.8和12公有的因数是哪几个？公有的最大因数是多少？（2）说一说你是怎么找出8和12公有的因数的.（3）引导学生学习公因数和最大公因数的概念.2.探究求最大公因数的1.（1）独自在练习本上找8和12公有的因数和最大因数，完成后汇报.生：8和12公有的因数有1，2，4，其中最大因数是4.（2）在组内交流找公有的因数的方法.生1：分别找出8和12的因数，再从中找出公有的因数.生2：通过集合图知道，1，2，4是8和12的公因数，其中4是最大的，叫方法.课件出示例2.引导学生用列举法和筛选法找出18和27的最大公因数. 做8和12的最大公因数.（3）自学教材第60页上面的内容.2.汇报自己喜欢的方法.（1）列举法：先分别找出18和27的因数，然后看18和27的因数中哪些是它们的公因数，再从中找出最大的一个.（2）筛选法：先找出两个数中较小数18的因数，再从中圈出较大数27的因数，最后找出最大的一个.括号里）（1）9和15的最大公因数是（）.①1 ②3 ③9 ④15（2）3和14的最大公因数是（）.①1 ②3 ③14 ④42（3）A是B的倍数，A、B两数的最大公因数是（）.①1 ②A ③B ④A、B的积答案：（1）②（2）①（3）③三、巩固练习，拓展延伸. （12分钟）1.完成教材第61页“做一做”第3题.2.引导学生完成教材第63页练习十五第1、2题.1.独自完成，同桌交流做完后的发现.2.学生独立完成，教师全班交流.教学过程中老师的疑问：四、课堂总结.（3分钟）1.通过今天这节课的学习，你有什么收获？2.布置课后作业.1.学生畅所欲言谈收获.2.完成课后作业.五、教学板书六、教学反思这节课是在掌握了因数、倍数、找因数的基础上进行教学的.通过找公因数的过程，让学生懂得找公因数的基本方法，在此基础上，引出公因数和最大公因数的概念.为了加深理解，进一步引导学生观察、分析、讨论，让学生明确找两个数的公因数的方法，并对找有特征的最大公因数的特殊方法有所体验.在教学中，教师重视让学生经历因数和最大公因数概念的形成过程，通过学生的操作活动能体会公因数的实际背景，加深对抽象概念的理解，也有利于改善学习方式，便于学生通过操作和交流学习过程，所以，学生的学习兴趣非常深厚，学习效果也很明显.。
个性化教学辅导教案学生姓名年级五年级学科数学上课时间年月日教师姓名课题分数的基本性质学习目标1.理解公因数和最大公因数的意义，探索出求最大公因数的方法.2.正确找出两个数的最大公因数.3.了解公因数和最大公因数在现实生活中的具体应用.4.知道什么是最简分数，掌握约分的方法.5.灵活运用约分的知识解决问题.6.能熟练运用约分的方法，正确地约分7.知道什么是两个数的公倍数和最小公倍数.8.运用公倍数和最小公倍数的知识解决问题.9.会比较同分母分数、同分子分数的大小.10.理解通分的意义，掌握通分的方法，能比较异分母分数的大小.教学过程教师活动学生活动1．一块长方形铁皮（如图），从四个角各切掉一个边长1cm 的正方形，然后做成盒子，这个盒子用了多少铁皮？它的容积有多大？2．如果a7能化成整数，那么（ ）A ．a 大于7B ．a 小于7C ．a 是7的倍数 D.无法确定3．把下列假分数化成带分数．135=________ 113=________ 218=________．4．如果23的分母加6，要使分数的大小不变，那么分子应加（ ） A ．8B ．6C ．4D ．25．化简分数.()1531= ()32745= ()34433= ()829= ()()3242418== ()4085= ____56____31÷=÷=．1．下面哪一句话是正确的？（ ） A ．12和45有公因数2 B ．12和45有公因数3 C ．12和45有公因数5D.以上都不对2．把一个分数约分，用分子和分母的（ ）去约，比较简便． A ．公约数B ．最小公倍数C ．最大公因数 D.因数3．下面（ ）不可以为23，14和56这三个分数的公分母． A ．6 B ．12C ．24D ．364．一个数的最大因数是15，这个数是 ，它有 个因数，这个数的最小倍数是 ．5．5A 和7B 通分得20B 和7B ，已知A ﹢B=45，那么B= ．6．一个真分数，它的分母比分子大33，约分后是47，这个分数原来是 ．7．两个不同的质数一定是互质数． ．（判断对错）8．约分时，每个分数越来越小；通分时，每个分数越来越大． （判断对错） 9．填一填．10．约分912= 2128= 1230=16250= 3654=11．通分58和71214，15和16912和524．学科分析 对应知识点：1.因数的概念；2.公因数的概念；3.最大公因数的概念.4.短除法求最大公因数；5.最小公倍数概念；6.约分的概念；7.通分的概念；关键原因：理解因数与倍数的求法，熟练根据分数的基本性质进行通分和约分； 学生分析最简分数：分数的分子和分母只有公因数1，像这样的分数叫做最简分数。
最大公因数与约分
学生姓名年级学科
授课教师日期时段
核心内容最大公因数、约分课型一对一/一对N
教学目标1、了解公因数、最大公因数在现实生活中的应用，并掌握求最大公因数的方法；
2、理解约分的意义，掌握约分的方法，并能准确判断约分的结果是不是最简分数；
3、分数的大小比较。
重、难点1、通过分数的性质学会分数的约分；
2、掌握求最大公因数的方法。
课首沟通
1.上次学习的分数的意义和性质都掌握了吗？
2.今天我们将继续学习分数的有关内容，你准备好了吗？
知识导图
课首小测
1. 如果a与b是两个不同的质数，那么a与b的最大公因数是（）。
2. A＝2×5×7，B＝2×2×3×5，A和B的最大公因数是（）。
3.六一儿童节那天，某慈善工会买了320个苹果、240个桔子、200个雪梨，去看望福利院的小朋友，问用这些果品，最多可以分成多少份同样的礼物？
4.求下列数的最大公因数。
5和6 64和16 24和56
导学一：最大公因数
知识点讲解 1：最大公因数
1.最大公因数：几个数相同的因数，叫做这几个数的公因数，其中最大的一个因数，叫这几个数的最大公因数。
例如：16的因数有（1、2、4、8、16），12的因数有（1、2、3、4、6、12），
12和16的公因数有（ 1、2、4 ），最大公因数是（ 4 ）。
当两个数成倍数关系时，最大公因数是那个较大的数。
如：13与52的最大公因数是（ 52 ）。
当两个数是互质数时，最大公因数是（ 1 ）。
2.寻找最大公因数的方法：
（1）分别找出这几个数的因数，再找出公有因数（或倍数）中最大（或最小）的一个；
（2）分解质因数：
24和36的最大公因数是：
（3）短除法：
24和36的最大公因数是：
3.互质数：公因数只有（）的两个数叫做互质数。
4.两个数互质的特殊判断方法：
（1）1和任何大于1的自然数互质。
（2）2和任何奇数都是互质数。
（3）相邻的两个自然数是互质数。
（4）相邻的两个奇数互质。
（5）不相同的两个质数互质。
（6）当一个数是合数，另一个数是质数时（除了合数是质数的倍数情况下），一般情况下这两个数也都是互质数。
例 1. 如果a、b互质（a和b都是自然数，且a，b≠0），则a和b的最大公因数是（）。
例 2. 已知a＝2×3×5，b＝2×3×11，则a、b的最大公因数是（）。
例 3. 用短除法求24和36的最大公因数。
例 4. 将一个长60厘米、宽45厘米、高75厘米的长方体，分割成同样大小的正方体，并使它们的体积尽可能大且没有多余，这些正方体的棱长是多少？可分割成多少个？
例 5. 某幼儿园大班老师借阅图书，如果借37本，平均分给每个小朋友后还剩1本；如果借56本，平均分给每个小朋友后还剩2本；如果借75本，平均分给每个小朋友后还剩3本。
这个班的小朋友最多有多少人？
例 6. 五年（2）班有男生24人，女生18人。
做操时要求男、女生分别排队，要使每排的人数都相同，每排最多有多少人？这是男、女生分别排了几排？
我爱展示
1.[单选题] 下面几组数中，两个数既是合数又是互质数的是（）。
A．11和15 B．24和18 C．35和36 D．17和23
2. [单选题] 在算式20＝4×5中，4和5是20的（）。
A．质因数B．素数C．因数D．互质数
3. [单选题] 甲数＝2×3×4，乙数＝3×4×5，甲和乙的最大公因数是（）。
A．6 B．12 C．15 D．120
4. m和n都是自然数，m÷n=8，m和n的最大公因数是（）。
5. A＝2×3×5，B＝2×5×7，A和B的最大公因数是（）。
6.求下面每组数的最大公因数。
①14，28，42 ②12，16，24
7.用短除法求42和54的最大公因数。
8.有三根木棒，一根长24米，一根长8米，一根长36米，要把它们截成同样长的小段，不许剩余，每段最长是多少米？一共可以截成多少段？
9.有铅笔433支，橡皮260块，平均分配给若干个小学生，分到最后铅笔余13支、橡皮余8块，问最多分给了多少个小学生？
10.有136支圆珠笔、89本笔记本和178个笔盒，平均奖给若干个优秀少先队员，结果圆珠笔多出1支，笔记本少1本，笔盒少2个，获奖的少先队员最多有多少人？
导学二：约分
知识点讲解 1：约分
1.最简分数：分子和分母只有公因数（ 1）的分数，叫做（最简分数）。
2.约分：把一个分数化成和它（大小相同），但分子和分母都比较小的分数，叫做约分。
举例：
例 1. 圈出最简分数，把不是最简分数的约分成最简分数。
例 2. 把约分成为最简分数：＝＝约分是运用了（）。
约分后分数的分子和分母发生了（），分数值（）。
例 3. 在○里填上“＜”、“＝”、“＞”。
○○○
例 4. [单选题] 把一个分数约分后，所得分数值与原来相比（）。
A.变大了
B. 变小了
C. 不变
例 5. 一批货物共400吨，已经运走了250吨，运走的占这批货物的几分之几？剩下的占这批货物的几分之几？
例 6. 把一个分数约分，用2约了两次，用3约了一次，得，原来这个数是多少？
我爱展示
1.分数单位是的最大真分数是（）；把这个最大的真分数化成分子是18而大小不变的分数是（）。
2.把、进行约分。
＝＝
3.在括号里填上最简分数。
131分＝（）小时2060克＝（）千克
109平方分米＝（）平方米
4.[单选题] 小红和小晴购买春游的食品，都花去了各自零花钱的，两人所花的钱相比，（）。
A.小红花的钱多
B.小晴花的钱多
C.一样多
D.不能确定谁花得多
5.（判断）一个分数的分子和分母都是合数，那么这个分数一定不是最简分数。
（）
6.把下面的分数化成分母是3而大小不变的分数。
7.在下列括号里填上适当的数。
（1）（2）
（3）（4）
限时考场模拟
1.在下面的括号里填上最简分数。
25分=（）时300dm3=（）m3
2.按要求填一填。
18和30的公因数有（），最大公因数是（）。
3.（判断）1是所有非0自然数的公因数。
（）
4.（判断）最简分数的分子、分母一定都是质数。
（）
5.[单选题] 如果一个分数的分子和分母（），则一定是最简分数。
A、都是奇数
B、都是偶数
C、两个不同的质数
D、一个是质数，一个是合数
6.某市有一个三角形公园，三边长分别为498米，612米，528米。
计划在公园周围每隔若干米植一棵樟树，并且每两棵之间的距离最远，每两棵树相隔多远？植了多少棵？
课后作业
1.分母是5的所有最简真分数有（），它们的和是（）。
2.在中，a是自然数，当a小于（）时，它是真分数，当a大于或等于（）时，它是假分数，当a是
（）的倍数时，它能化成整数。
3.五年级三个班分别有36人、48人、42人参加体育活动，要把他们分成人数相等的小组，但各班同学不能打乱，最多每组多少人？
4.有38支铅笔和41本练习本平均奖给若干个好少年，结果铅笔多出3支，练习本还缺1本。
得奖的好少年有多少人？
5.有两根钢管，一根长25米，一根长20米，把它们锯成同样长的小段，使每根不许有剩余，每段最长几米？一共要锯几次？
6.一个自然数，去除22少2，去除34也少2，这个自然数最大是几？
7.用一个数去除52，余4，再用这个数去除40，也余4，这个数最大是多少？
8.开学初，学校准备了96个黑板擦，72把扫帚，48个纸篓，平均分给各个班。
每一种物品的个数都对应相等，最多可分给多少个班？每种物品各几个？
1.上次的课后作业完成了吗？还有什么不懂的吗？
2.今天学习的内容是分数的最大公因数与约分，你掌握了吗？
3.回去记得完成课后练习，做到温故而知新。
