【三维设计】版高中数学 第一部分 3.2 第一课时 一元二次不等式的解法(1)应用创新演练 新人教A版5

《一元二次不等式解法》高中数学教案《一元二次不等式解法》高中数学教案（通用7篇）教案是教师为顺利而有效地开展教学活动，根据课程标准，教学大纲和教科书要求及学生的实际情况，以课时或课题为单位，对教学内容、教学步骤、教学方法等进行的具体设计和安排的一种实用性教学文书。

下面是店铺整理的《一元二次不等式解法》高中数学教案，欢迎大家分享。

《一元二次不等式解法》高中数学教案篇1下面从教材分析、教学目标分析、教学重难点分析、教法与学法、课堂设计、效果评价六方面进行说课。

一、教材分析（一）教材的地位和作用“一元二次不等式解法”既是初中一元一次不等式解法在知识上的延伸和发展，又是本章集合知识的运用与巩固，也为下一章函数的定义域和值域教学作铺垫，起着链条的作用。

同时，这部分内容较好地反映了方程、不等式、函数知识的内在联系和相互转化，蕴含着归纳、转化、数形结合等丰富的数学思想方法，能较好地培养学生的观察能力、概括能力、探究能力及创新意识。

（二）教学内容本节内容分2课时学习。

本课时通过二次函数的图象探索一元二次不等式的解集。

通过复习“三个一次”的关系，即一次函数与一元一次方程、一元一次不等式的关系；以旧带新寻找“三个二次”的关系，即二次函数与一元二次方程、一元二次不等式的关系；采用“画、看、说、用”的思维模式，得出一元二次不等式的解集，品味数学中的和谐美，体验成功的乐趣。

二、教学目标分析根据教学大纲的要求、本节教材的特点和高一学生的认知规律，本节课的教学目标确定为：知识目标——理解“三个二次”的关系；掌握看图象找解集的方法，熟悉一元二次不等式的解法。

能力目标——通过看图象找解集，培养学生“从形到数”的转化能力，“从具体到抽象”、“从特殊到一般”的归纳概括能力。

情感目标——创设问题情景，激发学生观察、分析、探求的学习激情、强化学生参与意识及主体作用。

三、重难点分析一元二次不等式是高中数学中最基本的不等式之一，是解决许多数学问题的重要工具。

3.2 一元二次不等式及其解法三维目标：1.深刻理解二次函数、一元二次方程与一元二次不等式的关系；2.掌握一元二次不等式的解法，能应用一元二次不等式、对应方程、函数之间的关系解决综合问题；3.会解高次不等式及分式不等式；4.会解含绝对值的不等式及含参数的一元二次不等式的解法；5.通过对一元二次不等式的解法的学习，使学生了解“函数与方程”、“数形结合”及“等价转换”的数学思想。

重点难点：教学重点：从实际问题中抽象出一元二次不等式模型，围绕一元二次不等式的解法展开，突出体现数学结合的思想，熟练地掌握一元二次不等式的解法。

教学难点：深刻理解“三个二次”之间的联系。

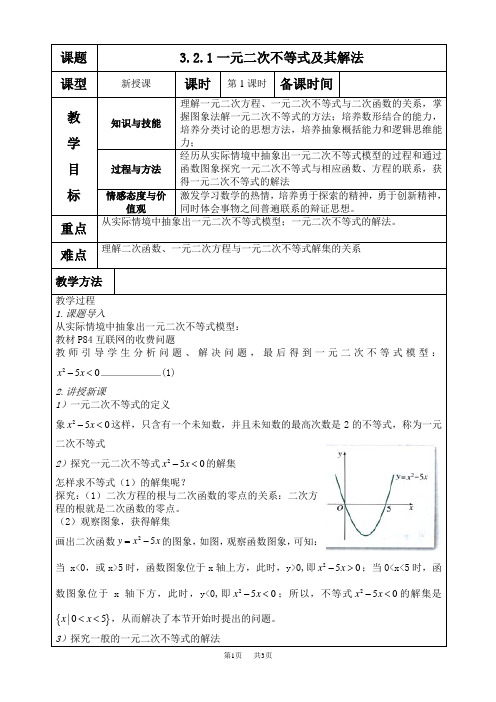
课时安排：3课时教学过程：第一课时（一）自主探究：1. 一元二次不等式的定义： 一般表达形式为：2. 一元二次不等式与相应函数、方程的联系：一元二次不等式经过变形，可以化成以下两种标准形式： ①ax 2 + b x + c>0(a>0) ② ax 2 + b x + c<0 (a>0)上述两种形式的一元二次不等式的解集，可通过方程ax 2 + b x + c=0的根来确定，设△=ac b 42-，则：（1）当△>0时，方程ax 2 + b x + c=0 有两个 的解21,x x ，设21x x <，则不等式①的解集为 不等式②的解集为 （2）当△=0时，方程ax 2 + b x + c=0有两个 的解，即21x x =，此时不等式①的解集为 不等式②的解集为（3）当△<0时，方程ax 2 + b x + c=0无实数解，则不等式①的解集为 不等式②的解集为方程20(0)a xb xc a ++=> 的判别式及根的情况240b ac ∆=-> 方程有二根x 、x （12x x <）240b a c ∆=-= 方程有一根x （12x x =） 240b ac ∆=-< 方程无实根2(0)y a x b x c a =++> 的图像不等式20(0)a xb xc a ++>> 的解集不等式20(0)a xb xc a ++≥> 的解集不等式20(0)a xb xc a ++<> 的解集不等式20(0)a xb xc a ++≤> 的解集3.一元二次不等式的解法步骤：①化二次项系数为正数；②计算判别式∆，分析不等式对应的方程的解的情况； ③结合图象写出解集。

第一部分 第三章 3.2 第二课时 一元二次不等式的解法（2）应用创新演练1．(2011·江西高考)若集合A ＝{x |－1≤2x ＋1≤3}，B ＝{x |x －2x≤0}，则A ∩B ＝( ) A ．{x |－1≤x ＜0} B ．{x |0＜x ≤1} C ．{x |0≤x ≤2}D ．{x |0≤x ≤1}解析：∵A ＝{x |－1≤x ≤1}，B ＝{x |0＜x ≤2}， ∴A ∩B ＝{x |0＜x ≤1}． 答案：B2．(2011·南宁模拟)在R 上定义运算⊗：x ⊗y ＝x (1－y )．若不等式(x －a )⊗(x ＋a )<1对任意实数x 成立，则( )A ．－1<a <1B ．0<a <2C ．－12<a <32D ．－32<a <12解析：由定义知(x －a )⊗(x ＋a )<1对任意实数x 成立，即(x －a )(1－x －a )<1对任意实数x 成立，∴x 2－x －a 2＋a ＋1>0恒成立． ∴Δ＝1－4×(－a 2＋a ＋1)<0. ∴－12<a <32.答案：C3．已知关于x 的不等式ax ＋b >0的解集是(1，＋∞)，则关于x 的不等式ax －bx －2>0的解集是( )A ．(－∞，－1)∪(2，＋∞)B ．(－1,2)C ．(1,2)D ．(2，＋∞)解析：依题意，a >0且－b a＝1.ax －b x －2>0⇔(ax －b )(x －2)>0⇔(x －ba)(x －2)>0， 即(x ＋1)(x －2)>0⇒x >2或x <－1. 答案：A4．如果不等式2x 2＋2mx ＋m 4x 2＋6x ＋3<1对一切实数x 均成立，则实数m 的取值范围是( )A ．(1,3)B ．(－∞，3)C ．(－∞，1)∪(2，＋∞)D ．(－∞，＋∞)解析：由4x 2＋6x ＋3＝(2x ＋32)2＋34>0对一切x ∈R 恒成立，从而原不等式等价于2x 2＋2mx ＋m <4x 2＋6x ＋3(x ∈R)⇔2x 2＋(6－2m )x ＋(3－m )>0对一切实数x 恒成立⇔Δ＝(6－2m )2－8(3－m )＝4(m －1)(m －3)<0，解出1<m <3. 答案：A5．(2011·上海高考)不等式x ＋1x≤3的解为________． 解析：x ＋1x ≤3⇔x ＋1x －3≤0⇔2x －1x ≥0⇔x (2x －1)≥0且x ≠0⇔x <0或x ≥12. 答案：x <0或x ≥126．有纯农药液一桶，倒出8升后用水补满，然后又倒出4升后再用水补满，此时桶中的农药不超过容积的28%，则桶的容积的取值范围是________．解析：设桶的容积为x 升，那么第一次倒出8升纯农药液后，桶内还有(x －8)（x >8）升纯农药液，用水补满后，桶内纯农药液的浓度x －8x. 第二次又倒出4升药液，则倒出的纯农药液为x －x升，此时桶内有纯农药液[(x－8)－x －x]升．依题意，得(x －8)－x －x≤28%·x .由于x >0，因而原不等式化简为 9x 2－150x ＋400≤0， 即(3x －10)(3x －40)≤0. 解得103≤x ≤403,又x >8，∴8< x ≤403.答案：(8，403]7．若不等式kx 2＋2kx ＋(k ＋2)<0对于一切x (x ∈R)的解集为∅，求实数k 的取值范围． 解：当k ＝0时，原不等式化为2<0，显然x ∈∅，符合题意，当k ≠0时，令y ＝kx 2＋2kx＋(k ＋2)，因为原不等式的解集为∅，即y <0无解，说明y ≥0恒成立，则⎩⎪⎨⎪⎧k >0，`Δ＝4k 2－k ＋k ≤0，由此解得k >0.综上所述，实数k 的取值范围是[0，＋∞)．8．汽车在行驶中，由于惯性作用，刹车后还要继续向前滑行一段距离才能停住，我们称这段距离为“刹车距离”．刹车距离是分析事故的一个重要因素．在一个限速40 km/h 以内的弯道上，甲、乙两辆汽车相向而行，发现情况不对，同时刹车，但还是相碰了，事发后现场测得甲车的刹车距离略超过12 m ，乙车的刹车距离略超过10 m ，又知甲、乙两种车型的刹车距离s (m)车速x (km/h)之间有如下关系：s 甲＝0.1x ＋0.01x 2，s 乙＝0.05x ＋0.05x 2.问：超速行驶应负主要责任的是谁？解：由题意列出不等式组⎩⎪⎨⎪⎧0.1x ＋0.1x 2>12，0.05x ＋0.005x 2>10，分别求解，得⎩⎪⎨⎪⎧x <－40或x >30，x <－50或x >40.由于x >0，从而可得x 甲>30 km/h ，x 乙>40 km/h. 经比较知乙车超过限速，应负主要责任．。

课时跟踪检测(十五) 一元二次不等式及其解法一、选择题1．下列不等式①x 2＞0；②－x 2－x ≤5；③ax 2＞2；④x 3＋5x －6＞0；⑤mx 2－5y ＜0；⑥ax 2＋bx ＋c ＞0.其中是一元二次不等式的有( )A ．5个B ．4个C ．3个D ．2个2．不等式9x 2＋6x ＋1≤0的解集是( )A.⎩⎨⎧⎭⎬⎫x |x ≠－13B.⎩⎨⎧⎭⎬⎫x |－13≤x ≤13C ．∅D.⎩⎨⎧⎭⎬⎫x |x ＝－133．设集合M ＝{x |x 2－x ＜0}，N ＝{x ||x |＜2}，则( ) A ．M ∩N ＝∅ B ．M ∩N ＝M C ．M ∪N ＝MD ．M ∪N ＝R4．关于x 的一元二次不等式ax 2＋bx ＋c ＜0的解集是全体实数的条件是( )A.⎩⎪⎨⎪⎧ a ＞0Δ＞0B.⎩⎪⎨⎪⎧ a ＞0Δ＜0C.⎩⎪⎨⎪⎧a ＜0Δ＞0D.⎩⎪⎨⎪⎧a ＜0Δ＜05．不等式x 2－|x |－2<0的解集是( ) A ．{x |－2<x <2} B ．{x |x <－2或x >2} C ．{x |－1<x <1} D ．{x |x <－1或x >1}二、填空题6．不等式x (3－x )≥x (x ＋2)＋1的解集是________．7．不等式组⎩⎪⎨⎪⎧x 2－1＜0，x 2－3x ＜0的解集为________．8．已知2a ＋1＜0，关于x 的不等式x 2－4ax －5a 2＜0的解集是________． 三、解答题9．已知ax 2＋2x ＋c ＞0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－13＜x ＜12，试求a ，c 的值，并解不等式－cx 2＋2x －a ＞0.10．解关于x 的不等式：ax 2－2≥2x －ax (a <0)．答 案课时跟踪检测(十五)1．选D 根据一元二次不等式的定义知①②正确．2．选D 不等式可化为(3x ＋1)2≤0，因此只有x ＝－13，即解集为⎩⎨⎧⎭⎬⎫x |x ＝－13，故选D.3．选B ∵M ＝{x |0＜x ＜1}，N ＝{x |－2＜x ＜2}， ∴MN ，即M ∩N ＝M .4．选D 由于不等式ax 2＋bx ＋c ＜0的解集为全体实数，所以，与之相对应的二次函数y ＝ax 2＋bx ＋c 的图象恒在x 轴下方，则有⎩⎪⎨⎪⎧a ＜0，Δ＜0.5．选A 令t ＝|x |，则原不等式可化为t 2－t －2<0，即(t －2)(t ＋1)<0.∵t ＝|x |≥0.∴t －2<0.∴t <2. ∴|x |<2，得－2<x <2.6．解析：原不等式即为3x －x 2≥x 2＋2x ＋1， 可化为2x 2－x ＋1≤0， 由于判别式Δ＝－7＜0， 所以方程2x 2－x ＋1＝0无实数根， 因此原不等式的解集是∅. 答案：∅7．解析：由⎩⎪⎨⎪⎧x 2－1＜0，x 2－3x ＜0，得⎩⎪⎨⎪⎧－1＜x ＜1，0＜x ＜3，∴0＜x ＜1. 答案：{x |0＜x ＜1}8．解析：∵方程x 2－4ax －5a 2＝0的两个根为x 1＝－a ，x 2＝5a ， 又∵2a ＋1＜0，即a ＜－12，∴x 1＞x 2.故原不等式解集为{x |5a ＜x ＜－a }． 答案：{x |5a ＜x ＜－a }9．解：由ax 2＋2x ＋c ＞0的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－13＜x ＜12，知a ＜0，且方程ax 2＋2x ＋c ＝0的两根为x 1＝－13，x 2＝12，由根与系数的关系知⎩⎪⎨⎪⎧a ＜0，－13＋12＝－2a，－13×12＝c a ，解得a ＝－12，c ＝2.此时，－cx 2＋2x －a ＞0，即2x 2－2x －12＜0， 其解集为{x |－2＜x ＜3}．10．解：原不等式移项得ax 2＋(a －2)x －2≥0， 化简为(x ＋1)(ax －2)≥0. ∵a <0，∴(x ＋1)(x －2a)≤0.当－2<a <0时，2a≤x ≤－1；当a ＝－2时，x ＝－1； 当a <－2时，－1≤x ≤2a.综上所述，当－2<a <0时，解集为{x |2a≤x ≤－1}；当a ＝－2时，解集为{x |x ＝－1}； 当a <－2时，解集为{x |－1≤x ≤2a}．。