全国重点高中黄冈中学2015年自主招生(理科实验班)预录考试数学模拟试题(1)
- 格式:pdf
- 大小:180.90 KB
- 文档页数:2

绝密★启用前2015年普通高等学校招生全国统一考试黄冈中学适应性考试数学(理工类)本试卷共6页,22题.全卷满分150分.考试用时120分钟.★祝考试顺利★注意事项:1.答卷前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.用统一提供的2B 铅笔将答题卡上试卷类型A 后的方框涂黑.2.选择题的作答:每小题选出答案后,用统一提供的2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试题卷、草稿纸和答题卡上的非答题区域均无效.3.填空题和解答题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将试题卷和答题卡一并上交.一、选择题:本大题共10小题,每小题5分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数11z i,(其中i 为虚数单位),则||z ()A .1BC .2D .02.某校在高三第一次模拟考试中约有1000人参加考试,其数学考试成绩近似服从正态分布,即2(100,)(0)X N a a ,试卷满分150分,统计结果显示数学考试成绩不及格(低于90分)的人数占总人数的110,则此次数学考试成绩在100分到110分之间的人数约为()A .400B .500C .600D .8003.下列判断中正确的是()A .命题“若1a b ,则2212a b”是真命题B .“12a b”是“114a b”的必要不充分条件C .若非空集合,,A B C 满足A B C ,且B 不是A 的子集,则“x C ”是“x A ”的充分不必要条件D .命题“2000,12x R x x ”的否定是“2,12x R x x ”4.已知数列 n a 的首项为11a ,且满足对任意的*n N ,都有12nn n a a 成立,则2015a ()A .201421 B .201521 C .201521 D .2016211C 2C 3C 1B 2B 3B 1P 2P 10P5.公元前3世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(V )与它的直径(D )的立方成正比”,此即3V kD ,欧几里得未给出k 的值.17世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式3V kD 中的常数k 称为“立圆率”或“玉积率”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式3V kD 求体积(在等边圆柱中,D 表示底面圆的直径;在正方体中,D 表示棱长).假设运用此体积公式求得球(直径为a )、等边圆柱(底面圆的直径为a )、正方体(棱长为a )的“玉积率”分别为1k 、2k 、3k ,那么123::k k k ()A .111::46 B .::264C .2:3:2D .::1646.已知结论:“在ABC 中,各边和它所对角的正弦比相等,即sin sin sin a b cA B C”,若把该结论推广到空间,则有结论:“在三棱锥A BCD 中,侧棱AB 与平面ACD 、平面BCD 所成的角为 、 ,则有()”A .sin sin BC ADB .sin sin AD BCC .sin sin BCD ACDS SD .sin sin ACD BCDS S7.把函数()sin ([0,2])f x x x 的图像向右平移3个单位后得到函数()g x 的图像,则()f x 与()g x 的图像所围成的面积为()A .1BC .D .28.设不等式组2210x y y表示的平面区域为M ,不等式组00x ty 表示的平面区域为N .在M 内随机取一个点,这个点在N 内的概率的最大值为()A .2B .1C .4D .129.如图,三个边长为2的等边三角形有一条边在同一条直线上,边33B C 上有10个不同的点1210,,P P P ,记2(1,2,,10)i i m AB APi,则1210m m m的值为()A .180B.C .45D .10.已知抛物线:C 24y x ,过定点(2,0)作垂直于x 轴的直线交抛物线于点M 、N ,若P 为抛物线C 上不同于M 、N 的任意一点,若直线PM 、PN 的斜率都存在并记为1k 、2k ,则1211||k k ()A .2B .1C.D.二、填空题:本大题共6个小题,考生共需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号.......的位置上.答错位置,书写不清,模棱两可均不得分.(一)必考题(11—14题)11.二项式52x的展开式中的常数项为.12.如下图,如果执行程序框图,输入正整数5,3n m ,那么输出的p 等于.13.棱锥的三视图如图所示,且三个三角形均为直角三角形,则yx 11 的最小值为.第12题图第13题图14.设定义域为R 的函数2|lg |,0()2,0x x f x x x x ,若关于x 的函数22[()]2()1y f x bf x 有8个不同的零点,则实数b 的取值范围是.(二)选考题(请考生在第15、16两题中任选一题做答,请先在答题卡指定位置将你所选的题目序号所在方框用2B 铅笔涂黑.如果全选,则按第15题作答结果计分.)21y x主视图俯视图左视图15.(选修4—1:几何证明选讲)如图,在圆O 中,直径AB 与弦CD 垂直,垂足为E ,EF DB ,垂足为F ,若6AB ,1AE ,则DF DB ________.16.(选修4-4:坐标系与参数方程)在直角坐标系xoy 中,曲线1C 的参数方程为sin cos 3y x ,( 为参数),以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为24)4sin(.设P 为曲线1C 上的动点,则点P 到2C 上点的距离的最小值为_________.三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.17.(本题满分12分)已知23sin cos 02f x x x x的最小正周期为T .(Ⅰ)求23f的值;(Ⅱ)在ABC 中,角A B C 、、所对应的边分别为a b c 、、,若有2cos cos a c B b C ,则求角B 的大小以及 f A 的取值范围.18.(本题满分12分)一台仪器每启动一次都随机地出现一个5位的二进制数12345A a a a a a ,其中A 的各位数字中11a ,(2,3,4,5)k a k 出现0的概率为13,(2,3,4,5)k a k 出现1的概率为23,记12345X a a a a a .当启动仪器一次时,(Ⅰ)求3X 的概率;(Ⅱ)求随机变量X 的分布列及X 的数学期望,并指出当X 为何值时,其概率最大.A19.(本题满分12分)如图,三角形ABC 和梯形ACEF 所在的平面互相垂直,AB BC ,//,2AF AC AF CE ,G 是线段BF 上一点,2AB AF BC .(Ⅰ)当GB GF 时,求证://EG 平面ABC ;(Ⅱ)求二面角E BF A 的正弦值;(Ⅲ)是否存在点G 满足BF 平面AEG ?并说明理由.20.(本题满分12分)若数列 n x 满足:111n nd x x (d 为常数,*n N ),则称 n x 为调和数列.已知数列 n a 为调和数列,且11a ,123451111115a a a a a .(Ⅰ)求数列 n a 的通项n a ;(Ⅱ)数列2n n a的前n 项和为n S ,是否存在正整数n ,使得2015n S ?若存在,求出n 的取值集合;若不存在,请说明理由.21.(本题满分13分)已知椭圆2222:1(0)x yC a ba b的左右焦点分别为12,F F,点B为短轴的一个端点,260OF B.(Ⅰ)求椭圆C的方程;(Ⅱ)如图,过右焦点2F,且斜率为(0)k k的直线l与椭圆C相交于,D E两点,A为椭圆的右顶点,直线,AE AD分别交直线3x于点,M N,线段MN的中点为P,记直线2PF的斜率为k .试问k k是否为定值?若为定值,求出该定值;若不为定值,请说明理由.22.(本题满分14分)定义:若()kf xx在[,)k 上为增函数,则称()f x为“k次比增函数”,其中k N,已知()axf x e.(其中 2.71238e )(Ⅰ)若()f x是“1次比增函数”,求实数a的取值范围;(Ⅱ)当12a 时,求函数()()f xg xx在[,1](0)m m m上的最小值;(Ⅲ)求证:72e.。
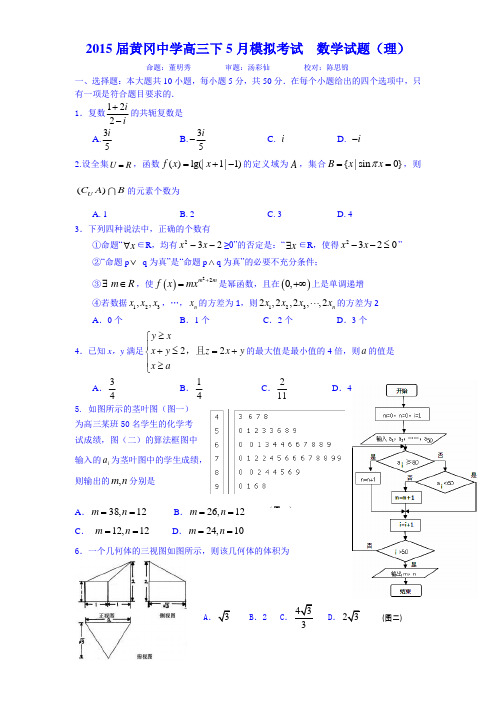
(图二)2015届黄冈中学高三下5月模拟考试 数学试题(理)命题:董明秀 审题:汤彩仙 校对:陈思锦一、选择题:本大题共10小题,每小题5分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的. 1.复数122ii+-的共轭复数是 A.35iB.35i -C. iD. i -2.设全集U R =,函数()lg(|1|1)f x x =+-的定义域为A ,集合{|sin 0}B x x π==,则()U C A B 的元素个数为A. 1B. 2C. 3D. 43.下列四种说法中,正确的个数有①命题“x ∀∈R ,均有232x x --≥0”的否定是:“x ∃∈R ,使得2320x x --≤”②“命题p ∨ q 为真”是“命题p ∧q 为真”的必要不充分条件; ③∃m R ∈,使()22m mf x mx+=是幂函数,且在()0,+∞上是单调递增④若数据123,,x x x ,…,n x 的方差为1,则1232,2,2,,2n x x x x ⋅⋅⋅的方差为2 A .0个B .1个C .2个D .3个4.已知x ,y 满足22y x x y z x y x a ≥⎧⎪+≤=+⎨⎪≥⎩,且的最大值是最小值的4倍,则a 的值是A .34 B .14 C .211D .4 5. 如图所示的茎叶图(图一) 为高三某班50名学生的化学考 试成绩,图(二)的算法框图中 输入的i a 为茎叶图中的学生成绩, 则输出的n m ,分别是A .12,38==n mB .26,12m n ==C . 12,12m n ==D .24,10m n ==6.一个几何体的三视图如图所示,则该几何体的体积为A .3B .2C .433D .23(图一)7.先后掷一枚质地均匀骰子(骰子的六个面上分别标有1、2、3、4、5、6个点)两次,落在水平桌面后,记正面朝上的点数分别为x ,y ,设事件A 为“y x +为偶数”, 事件B 为“x ,y 中有偶数且y x≠”,则概率)|(A B P 等于A .31 B .21 C .61 D .41 8.设函数sin ()11cos xf x x=++的所有正的零点从小到大依次为,.....,,321x x x .设1232015....x x x x α=++++,则cos α的值是A.0B.23-C.23D.1 9. 过曲线22122:1(0,0)x y C a b a b-=>>的左焦点1F 作曲线2222:C x y a +=的切线,设切点为M ,延长1F M 交曲线23:2(0)C y px p =>于点N ,其中13C C 、有一个共同的焦点,若1MF MN =,则曲线1C 的离心率为B.51-C.51+ 10.已知非零向量,,a b c 满足||||4a b b -==,()()0a c b c -⋅-=,若对每一个确定的b ,||c 的最大值和最小值分别为,m n ,则m n -的值为A.随||a 增大而增大B. 随||a 增大而减小C.是2D. 是4 二、填空题:本大题共6个小题,考生共需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分. (一) 必考题(11—14题)11.若1)nx的二项展开式中各项的二项式系数的和是64,展开式中的常数项为 ___________(用数字作答).12.已知等差数列{}n a 满足2420122014032a a a a π+++=⎰,n S 是该数列的前n项的和,则2015S = .13.计算12323nn n n n C C C nC +++⋅⋅⋅+,可以采用以下方法:构造等式: 0122n n n n n n C C x C x C x +++⋅⋅⋅+()1nx =+,两边对x 求导,得()112321231n n n n n n n C C x C x nC x n x --+++⋅⋅⋅+=+,在上式中令1x =,得1231232n n n n n n C C C nC n -+++⋅⋅⋅+=⋅.类比上述计算方法, 计算12223223nn n n n C C C n C +++⋅⋅⋅+=_________.14.如果)(x f y =的定义域为R ,对于定义域内的任意x ,存在实数a 使得)()(x f a x f -=+成立,则称此函数具有“)(a P 性质”. 给出下列命题:①函数x y sin =具有“)(a P 性质”;②若奇函数)(x f y =具有“)2(P 性质”,且1)1(=f ,则(2015)1f =;③若函数)(x f y =具有“(4)P 性质”, 图象关于点(10),成中心对称,且在(1,0)-上单调递减,则)(x f y =在(2,1)--上单调递减,在(1,2)上单调递增;④若不恒为零的函数)(x f y =同时具有“)0(P 性质”和 “(3)P 性质”,且函数)(x g y =对R x x ∈∀21,,都有1212|()()||()()|f x f x g x g x -≥-成立,则函数)(x g y =是周期函数. 其中正确的是(写出所有正确命题的编号).(二) 选考题(请考生在第15、16两题中任选一题做答,请先在答题卡指定位置将你所选的题目序号所在方框用2B 铅笔涂黑.如果全选,则按第15题作答结果计分.) 15.如图,圆A 与圆B 交于C 、D 两点,圆心B 在圆A 上,DE 为圆B 的直径,已知4,1==DE CE ,则圆A 的半径为_______.16.在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.若点P 为直线cos sin 40ρθρθ--=上一点,点Q 为曲线2(14x t t y t =⎧⎪⎨=⎪⎩为参数)上一点,则||PQ 的最小值为 .三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.17. (本小题满分12分)在锐角△ABC 中,222cos()sin cos b a c A C ac A A--+=.(Ⅰ)求角A ; (Ⅱ)若2a =,当7sin cos()12B C π+-取得最大值时,求B 和b . 18.(本小题满分12分) 黄冈市于2014年12月29日起实施小汽车限购政策.根据规定,每年发放10万个小汽车名额,其中电动小汽车占20%,通过摇号方式发放,其余名额通过摇号和竞价两种方式各发放一半.政策推出后,某网站针对不同年龄段的申请意向进行了调查,结果如下表所示:申请意向年龄摇号竞价(人数)合计 电动小汽车(人数)非电动小汽车(人数)30岁以下(含30岁) 50 100 50 200 30至50岁(含50岁)50 150 300 500 50岁以上 100 150 50 300 合计2004004001000(Ⅰ)采取分层抽样的方式从30至50岁的人中抽取10人,求其中各种意向人数; (Ⅱ)在(Ⅰ)中选出的10个人中随机抽取4人,求其中恰有2人有竞价申请意向的概率; (Ⅲ)用样本估计总体,在全体市民中任意选取4人,其中摇号申请电动小汽车意向的人数记为ξ,求ξ的分布列和数学期望.19.(本小题满分12分)已知四边形ABCD 满足AD ∥BC ,BA =AD =DC =21BC =a ,E 是BC 的中点,将△BAE 沿AE 折起到1B AE ∆的位置,使平面1B AE ⊥平面AECD ,F 为B 1D 的中点.(Ⅰ)证明:B 1E ∥平面ACF ;(Ⅱ)求平面ADB 1与平面ECB 1所成锐二面角的余弦值.20.(本小题满分12分)设数列}{n a 的前n 项和为n S ,满足4231-⋅-=++n n n n a S ,*N ∈n ,且42,,321+a S a 成等比数列.(Ⅰ)求1a ,2a ,3a 的值; (Ⅱ)设2n n n a b =,n N *∈,求{}n a 的通项公式.21.(本小题满分13分)已知椭圆2222:1x y C a b += (0)a b >>的离心率为636.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)设F 为椭圆C 的右焦点,T 为直线(,2)x t t R t =∈≠上纵坐标不为0的任意一点,过F 作TF 的垂线交椭圆C 于点P ,Q .(ⅰ)若OT 平分线段PQ (其中O 为坐标原点),求t 的值; (ⅱ)在(ⅰ)的条件下,当||||PQ TF 最小时,求点T 的坐标.22. (本小题满分14分)已知x eexx g m x a mx x f =--=)(,ln )(( 2.71828)e =,其中a m ,均为实数.(Ⅰ)求)(x g 的极值; (Ⅱ)设1,0m a ,求证:对[]2112122121,3,4(),()()()()ex ex x x x x f x f x g x g x ∀∈≠-<-恒成立;(Ⅲ)设2=a ,若对∀给定的(]e x ,00∈,在区间(]e ,0上总存在)(,2121t t t t ≠使得)()()(021x g t f t f ==成立,求m 的取值范围.答 案15- DCCBB 610- CAADD11.15 12. 4030 13. 2(1)2n n n -+⋅ 14. ①③④ 15. 4 16.32217.18.19(1)连结ED 交AC 于O ,连结OF ,因为AECD 为菱形,OE=OD 所以FO ∥B 1E , 所以1//B E ACF 面。


x第8题 2015年秋一中预录模拟题数学试题(5)时间:100分钟 分数:100分一、选择题(5×5=25)1、若d c b a <<<<0,则以下四个结论中,正确的是( ) A 、d c b a +++一定是正数 B 、b a c d --+可能是负数 C 、a b c d ---一定是正数 D 、a b d c ---一定是正数2、022=-+-x x ,那么x 的取值范围是( ) A 、2>x B 、2<x C 、2≥x D 、2≤x3、已知实数a 、b 满足条件0454422=++-+b a b a ,那么-ab 的平方根是( )A 、2±B 、2C 、21±D 、214、在△ABC 中,∠B=45°,AC 的垂直平分线交AC 于D ,交BC 于E ,且∠EAB :∠CAE=3:1,则∠C=( )A 、27°B 、25°C 、22.5°D 、20°5、已知Rt △ABC 中,∠C=90°,∠A=30°,直线BC 或AC 上取一点P,使得△PAB 是等腰三角形,则符合条件的点P 有( )A 、2个B 、4个C 、6个D 、8个二、填空题(5×5=25)6、某商品按标价的八折出售,可获利20%,若按标价出售,则利润率为 .7、已知关于x 的一次函数72-+=m mx y 在51≤≤-x 上的函数值总是正数,则m 的取值范围是 .8、在直角坐标系中,矩形OABC 的顶点B 在坐标为(15,6),直线b x y +=31恰好将矩形OABC 分成面积相等的两部分,那么b= .9、如图,C 在线段AB 上,在AB 同侧作等边△ACM 和△BCN ,连AN,BM ,若∠MBN=38°,则∠ANB 的大小为 .10、如图,S △ABC =1,若S △BDE = S △DEC = S △ACE ,则S △ADE = .三、解答题(12+12+12+14)11、已知△ABC 为等边三角形,延长BC 到M ,CA 到N ,使CM=AN ,连BN 交MA 的延长线于Q ,求∠BQM .12、下表为装运甲、乙、丙三种蔬菜的重量及利润,某汽车公司计划装运甲、乙、丙三种蔬菜到外地(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A 地销售,问装运乙、丙两种蔬菜的汽车各多少辆? (2)公司计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B 地销售(每种蔬菜不少于一车),如何装运,可使公司获得最大利润,最大利润是多少?CMA CB 第5题 AC B 第9题 EC 第4题AB CDE第10题13、若n满足1)2006()2005(22=-+-nn,求)2005)(2006(--nn的值。


黄冈中学2015年自主招生模拟考试数 学 试 题(满分:100分 考试时间:90分钟)本试题分二卷,第一卷为选择题与填空题,第二卷为解答题,请将选择题与填空题的答案写在第二卷的相应位置上。
第一卷一、选择题(每小题3分,共8小题,在给出的四个选项中,只有一项是符合题目要求的.请将答案写在第二卷的相应位置上...............) 1.已知圆锥的底面半径为9㎝,母线长为30㎝,则圆锥的侧面积为( )A .270πcm 2B .360πcm 2C .450πcm 2D .540πcm 22.如果有2007名学生排成一列,按1、2、3、4、5、4、3、2、1、2、3、4、5、4、3、2、1、……的规律报数,那么第2007名学生所报的数是( )A . 2B . 3C . 4D .53.书架上有两套同样的教材,每套分上、下两册,在这两套教材中随机抽取两册,恰好组成一套教材的概率是( )A .23 B .13 C .12 D .164.要使关于x 的方程21212-+=--++x x ax x x x 的解是正数,a 应满足的条件是( ) A .1->a B . 1-<a C .1->a 且3≠a D .1-<a 且3-≠a 5.如图,边长为1的正方形ABCD 绕点A 按逆时针方向旋转30︒到正方形AB C D ''',则图中阴影部分的面积为( ) A .313-B .33C .314-D .126.方程1xy x y ++=的整数解的组数为( )A .2B .4C .6D .8 7.如图,∠ACB =60○,半径为2的⊙0切BC 于点C ,若将⊙O 在CB上向右滚动,则当滚动到⊙O 与CA 也相切时,圆心O 移动的水平距离为( )A .2πB .4πC .32D .48.a 、b 是方程()2570x m x +-+=的两个根,则()()2277a ma b mb ++++=( )AcoA .365B .245C .210D .175 二、填空题(每小题3分,共8小题,请将答案写在第二卷的相应位置上...............) 9.作抛物线1C 关于x 轴对称的抛物线2C ,将抛物线2C 向左平移2个单位,向上平移1个单位,得到的抛物线C 的函数解析式是()2211y x =+-,则抛物线1C 所对应的函数解析式是10.如图,△ABC 的外接圆的圆心坐标为 。
2015年黄冈中学提前录取数学模拟试题(2)2015.3.20(总分:120分 考试时间:120分钟)一、选择题(本大题共10个小题,每小题3分,共30分。
四个选项中只有一项是正确的)1、由四个相同的小正方体搭建了一个积木,它的三视图如图所示,则这个积木可能是( )A B C D2、黄冈市地处湖北省东部,大别山南麓,长江北岸,下辖一区七县两市,总人口740万人,人口总数用科学记数法表示为( )A 、70.4×105人 B 、7.4×106人 C 、7.4×105人 D 、7.4×104人 3、已知一元二次方程x 2-4x+3=0两根为x 1、x 2,则x 1·x 2=( ) A 、4B 、3C 、-4D 、-34、下列四个点中,有三个点同在反比例函数y=xk的图象上,则不在这个函数图象上的点是( ) A 、(5,1) B 、(-3,-35)C 、(35,3)D 、(-1,5)5、如图,直径AB 为6的半圆,绕A 点逆时针旋转60°,此时点B到了点B ’,则图中阴影部分的面积是( ) A 、3πB 、6πC 、5πD 、4π6、已知函数y=31++-x x 的最大值为M ,最小值为m ,则Mm的值为( ) A 、41 B 、21 C 、22 D 、23 7、在平面直角坐标系中,O 为坐标原点,直线L 是函数y=-3x 的图象,点A 的坐标为(1,0),在直线L 上找一个点N ,使△ONA 是等腰三角形,则符合条件的点N 的个数是( ) A 、2个B 、3个C 、4个D 、5个8、警方抓获一个由甲、乙、丙、丁四人组成的盗窃团伙,其中有一人是主谋,经过审讯,A 、B 、C 三名警察各自得出结论,A :主谋只有可能是甲或乙;B :甲不可能是主谋;C :乙和丙都不可能是主谋。
已知三名警察中只有一人推测正确,则主谋是( ) A 、甲B 、乙C 、丙D 、丁9、团结号列车上午7:45从甲地出发开往乙地,胜利号列车上午8:15从乙地出发开往甲地。
黄冈中学2015年自主招生模拟考试数学模拟试题A 卷时间120分钟 分数100分一、选择题(请把唯一答案的序号填在题后的括号内,每小题5分,共25分)1、已知a 、b 是实数,2022++=b a x ,)2(4a b y −=,则x 、y 的大小关系是( )A. x ≤yB. x ≥yC. x <yD. x >y2、在△ABC 中,∠A=30°,AB=4,BC=334,则∠B 为( ) A. 30°B. 90°C. 30°或60°D. 30°或90°3、如图1,在矩形ABCD 中,动点P 从点B 出发,沿BC 、CD 运动至点D 停止,设点P 运动的路程为x, △ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则BD 的长是( )A.13B.29C.4、已知a 2+4a+1=0,且32212324=+++−ama a ma a ,则m 的值为( )A.219B.219−C.19D.-195、如图3,梯形ABCD 中,AD ∥BC ,∠B=30°,∠C=60°, E 、F 、M 、N 分别为AB 、CD 、BC 、DA 的中点,若BC=7, MN=3,则EF 为( )A. 3B. 4C. 5D. 6二、填空题(每小题5分,共25分)6、若02722=+−x x ,则2424x x −=__________ 7、如图4,正方形ABCD 边长为1,动点P 从A 点出发,沿正方形的边接逆时针方向运动,当它的路程为2013时, 点P 所在的位置为_________;当点P 在D 点时,点P 运动的路程为__________(用含自然数n 的式子表示)。
8、如图5,将两张长为8,宽为2是_______形,其周长的最小值为______,最大值为_______。
9、已知51=−aa ,则aa 1−=__________ 10、如图6所示,点A 、C 都在函数)0(2>=x xy 的图象上, 点B 、D 都在x 轴上,且△OAB 、△BCD 都是等腰直角三角形, 则点D 的坐标为__________。