物理化学第三章习题解答

第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作。

求（1）热机效率；（2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3．2 卡诺热机在的高温热源和的低温热源间工作，求：（1）热机效率；（2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解：(1) 由卡诺循环的热机效率得出（2）3．3 卡诺热机在的高温热源和的低温热源间工作，求（1）热机效率；（2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（1）(2)3．4 试说明：在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时，若令卡诺热机得到的功r W 等于不可逆热机作出的功－W 。

假设不可逆热机的热机效率大于卡诺热机效率，其结果必然是有热量从低温热源流向高温热源，而违反势热力学第二定律的克劳修斯说法。

证： （反证法） 设 r ir ηη>不可逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等，即总的结果是：得自单一低温热源的热，变成了环境作功，违背了热力学第二定律的开尔文说法，同样也就违背了克劳修斯说法。

3．5 高温热源温度，低温热源温度，今有120KJ的热直接从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间。

求下列三种情况下，当热机从高温热源吸热时，两热源的总熵变。

（1）可逆热机效率。

（2）不可逆热机效率。

（3）不可逆热机效率。

解：设热机向低温热源放热，根据热机效率的定义因此，上面三种过程的总熵变分别为。

3.7 已知水的比定压热容。

今有1 kg，10℃的水经下列三种不同过程加热成100 ℃的水，求过程的。

（1）系统与100℃的热源接触。

（2）系统先与55℃的热源接触至热平衡，再与100℃的热源接触。

第五版物理化学第三章习题答案（）第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作。

求（1）热机效率；（2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3．2 卡诺热机在的高温热源和的低温热源间工作，求：（1）热机效率；（2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解：(1) 由卡诺循环的热机效率得出（2）3．3 卡诺热机在的高温热源和的低温热源间工作，求（1）热机效率；（2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（1）(2)3．4 试说明：在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时，若令卡诺热机得到的功r W 等于不可逆热机作出的功－W 。

假设不可逆热机的热机效率大于卡诺热机效率，其结果必然是有热量从低温热源流向高温热源，而违反势热力学第二定律的克劳修斯说法。

证：（反证法）设r ir ηη>不可逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等，即总的结果是：得自单一低温热源的热，变成了环境作功，违背了热力学第二定律的开尔文说法，同样也就违背了克劳修斯说法。

3．5 高温热源温度，低温热源温度，今有120KJ的热直接从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间。

求下列三种情况下，当热机从高温热源吸热时，两热源的总熵变。

（1）可逆热机效率。

（2）不可逆热机效率。

（3）不可逆热机效率。

解：设热机向低温热源放热，根据热机效率的定义因此，上面三种过程的总熵变分别为。

3.7 已知水的比定压热容。

今有1 kg，10℃的水经下列三种不同过程加热成100 ℃的水，求过程的。

（1）系统与100℃的热源接触。

第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作。

求（1）热机效率；（2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3．2 卡诺热机在的高温热源和的低温热源间工作，求：（1）热机效率；（2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解：(1) 由卡诺循环的热机效率得出（2）3．3 卡诺热机在的高温热源和的低温热源间工作，求（1）热机效率；（2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（1）(2)3．4 试说明：在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时，若令卡诺热机得到的功r W 等于不可逆热机作出的功－W 。

假设不可逆热机的热机效率大于卡诺热机效率，其结果必然是有热量从低温热源流向高温热源，而违反势热力学第二定律的克劳修斯说法。

证： （反证法） 设 r ir ηη>不可逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等，即总的结果是：得自单一低温热源的热，变成了环境作功，违背了热力学第二定律的开尔文说法，同样也就违背了克劳修斯说法。

3．5 高温热源温度，低温热源温度，今有120KJ的热直接从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间。

求下列三种情况下，当热机从高温热源吸热时，两热源的总熵变。

（1）可逆热机效率。

（2）不可逆热机效率。

（3）不可逆热机效率。

解：设热机向低温热源放热，根据热机效率的定义因此，上面三种过程的总熵变分别为。

3.7 已知水的比定压热容。

今有1 kg，10℃的水经下列三种不同过程加热成100 ℃的水，求过程的。

（1）系统与100℃的热源接触。

（2）系统先与55℃的热源接触至热平衡，再与100℃的热源接触。

第三章化学平衡1、气相反应：2SO3(g)=2SO2(g)+O2(g)在1000K 时的平衡常数K F=3.54 X 103,求该反应的K’(IOOOK) 和K/(1000K)。

解：第一问能做，第二问不能做(不知道系统总压) 。

解答略。

2、氧化钴(CoO)能被氢或CO还原为Co,在721 C、101325Pa时，以H2还原，测得平衡气相中出的体积分数H2=0.025 ;以CO还原，测得平衡气相中CO的体积分数H2 =0.0192。

求此温度下反应CO(g)+H 2O(g)=CO2(g)+H2(g)的平衡常数K 匕解：CoO(s) + H2(g) = Co(s) + H2O (1)0.025 ph (1-0.025) p71a1-0.025Q 390.025CoO(s) + CO(g) = Co(s) + CO2 (2)0.0192 (1-0.0192) p711 -0.0192510.0192(2)-(1)= CO(g)+H 2O(g)=CO2(g)+H2(g)，所以K/ - K// K/=51/39=1.313、计算加热纯Ag2O开始分解的温度和分解温度。

(1)在101325Pa的纯氧中；(2)在101325Pa且的空气中。

已知反应2Ag2O(s)=4Ag(s)+O 2(g)的.：r G m(T ) =(58576-122T/K)J • mol-1。

解：分解温度O2=0.21即标态下分解的温度。

令.l r G：(T ) =(58576-122T/K)<0，得T>480K开始分解温度即非标态下分解的温度。

令.「G m(T) =(58576-122T/K)+8.314 X Tin0.21<0，得T>434K4、已知Ag2O及ZnO在温度1000K时的分解压分别为240及15.7kPa。

问在此温度下(1)哪一种氧化物容易分解？ (2)若把纯Zn及纯Ag置于大气中是否都易被氧化？( 3)若把纯Zn、Ag、ZnO、Ag2O 放在一起，反应如何进行？(4)反应ZnO(s)+2Ag(s)=Zn(s)+Ag 2O(s)的• : r H m=242.09kJ - mol -,问增加温度时，有利于那种氧化物的分解？解：(1)氧化银易分解；(2)银不易被氧化；(3) Zn + Ag2O = Ag + ZnO ; (4) ZnO5、已知下列反应的冷G；-T关系为：A 5 1Si(s)+O2(g)=SiO2(s); ：r G m(T) =(-8.715 X 10 +181.09T/K)J • mol-A 5 12C(s)+O2(g)=2CO(g); ：r G m(T) =(-2.234 X 10 -175.41T/K)J • mol-试通过计算判断在1300K时，100kPa下，硅能否使CO还原为C?硅使CO还原的反应为：Si(s)+2CO(g)=SiO 2(s)+2C(s)解：(1) - (2) = (3),贝Ua 5 1：Qm(T) =(-6.481 X 10 +356.5T/K)J • mol-1300K 时，r G m(T) =(-6.481 X 105+356.5 X 1300)=-1.847 X 105J - mol-1<0,可以6、将含水蒸气和氢气的体积分数分别为0.97和0.03的气体混合物加热到1000K，这个平衡气体混合物能否与镍反应生成氧化物？已知Ni(s)+0.5O2=NiO(s); • :^1(1000 K ) =-146.11 kJ • mol-1解：查表得CO(g) +H2O(g) =CO 2(g) + H 2(g)：f H F(298K )-110.54 -241.84 -393.5 0 S m (298K )197.9188.74213.64130.58-1K -1 • molH 2(g)+0.5O 2(g)=H 2O(g); .-：r G ^(1000 K) =-191.08 kJ • mol -1解: (1) - (2) 得 Ni(s)+ H 2O(g)= NiO(s)+ H 2(g).■■■：r Gm(1000 K ) =-146.11 + 191.08 =44.97kJ • mol -1 .■■■：rGm (1000 K ) = . ：rGm (1000 K ) +RTInQ-1=44970+8.314 X 1000 X ln (0.03/0.97) =16.07 kJ • mol 反应不能正向进行。

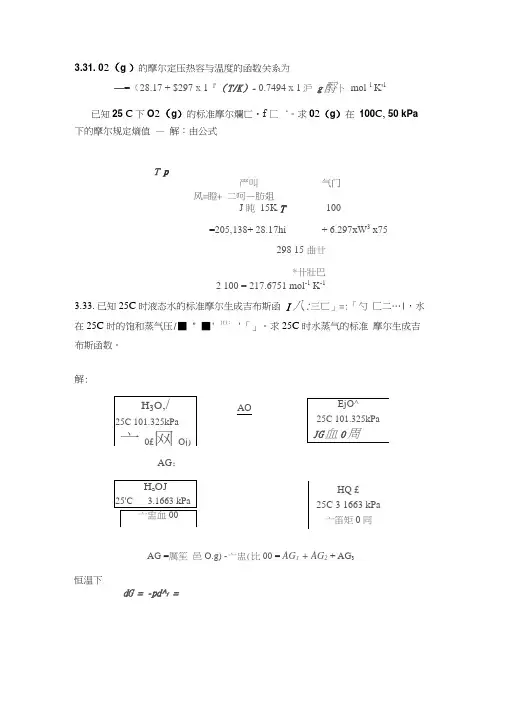
3.31. 02（g ）的摩尔定压热容与温度的函数关系为—=（28.17 + $297 x 1『（T/K ）- 0.7494 x 1沪 g 酹卜 mol _l K'1已知25 C 下O 2（g ）的标准摩尔爛匸•f 匚‘。

求02（g ）在 100C, 50 kPa 下的摩尔规定熵值 — 解：由公式T p严叫气门风=瞪+ 二呵—肪爼J 盹 15K T100=205,138+ 28.17hi+ 6.297xW 3 x75298 15 曲廿*卄壯巴2 100 = 217.6751 mol -1 K -13.33. 已知25C 时液态水的标准摩尔生成吉布斯函 I 八:三匸」=:「勺 匚二…|，水在25C 时的饱和蒸气压/■ " ■' lfl ； '「」。

求25C 时水蒸气的标准 摩尔生成吉布斯函数。

解:AG ；AG =厲笙 邑O.g) -亠盅(比00 = AG 1 + AG 2 + AG 3恒温下dG = -pd^f =AO对凝聚相恒温过程A。

佟0 , 可逆相变AG3= 0因此2：（H a O,g）= g（HQJ）- J；\松=3：（HQJ）- RTh旦' Pi=-237.129XW3- 298.152?In 丄竺100=-228.57 lkJ mol3.36已知在101.325 kPa下，水的沸点为100C，其比蒸发焓一--几已知液态水和水蒸气在100〜120C范围内的平均比定压热容分别为：■..J-.',' - ■ ■■-及」丁…：。

今有101.325 kPa下120°C的1 kg过热水变成同样温度、压力下的水蒸气。

设计可逆途径，并按可逆途径分别求过程的丄J及」」。

解：设计可逆途径如下A J¥=A//]+A//2 +A禺=叫0比- £) +沁Q +咖越)低-驾)=廉后)-讥血一爲)+沁卅= lx(2 033-4,224)X20+1X 2257.4= 2213.6kJ十』)ln J泌小+心九爲d卅373.15 1x2257.4 “ ° 心“ 393.15= 1x4.224In ---------- F ------------- +1x2.0331n ----------393.15 373.15 373.15=5.935 kJ K-1AG = AH-7hS= 2213.6 - 393.15 x 5.935= -119 77 kJ3.40化学反应如下：CH』g) + CO 血卜=2CO(g)+H2(g)(1)利用附录中各物质的S°m, △ f G °m数据，求上述反应在25 C时的△r S°m,△ r G m ；(2)利用附录中各物质的Af G em数据，计算上述反应在25C时的':'-L ;(3)25C，若始态CH4(g)和H2(g)的分压均为150 kPa，末态CO(g)和H2(g)的分压均为50 kPa,求反应的人r丄一解(1) 25 Q时题给反应的、瓷=S^H^B) = 2A f H^(C0J g)-^(044,8)^^(002^) B=|2x( - 110.525)- (-74.81)-(-393.509)}kJ-moP l= 247.269 kJ-mol-1irS® = S V B S S(B^)=2 S®(C0.g) + 2 S®(H3>g) - S软CH^g)-熏(COzQ=(2 X (197-674+130.684)-186.264 - 213.741 J*n»r u K_1= 256.712 J^mor^K-1=(247 ・ 269 - 298 ・ 15 x 256 ・ 712 x KT?)町・ mol -1 = 170.730 kJ ・moL所以 AS =AS(N 2) + ^S(H 2O) = (15.237+335.479 )J-K^ = 350.716 J-K^1TAS = 373.15 Kx350.716 J ・KT = 130.87 kJ dA = AU-TZ\S = (112.696-130.8刀 kJ=-18.174 kJAG - AZZ - TAS = (122.004 - 130.87)kJ - -8.866 kJ (2) 25t 时，=为"QG^(B,p )B= 2A f G2(CO,g)-A f G®(CH 4,g)-A f G®(CQ 2,g) =-(2 x 137.168 - 50.72 - 394.359)kJ • mol'1 =170.743 kJ-moP 1(3)由于参加反应的各物质皆不处于标准状态，所以，需要设计岀一条途 径，利用标准状态下反应的热力学函数变，计算在指定条件下的有关的函数变。

第三章 化学反应系统热力学 (习题答案) 2007-6-6§3.1 标准热化学数据 练习1 所有单质的 Om f G ∆ (T )皆为零?为什么?试举例说明?答：所有处于标准状态的稳定单质的O m f G ∆ (T )（因为生成稳定单质，稳定单质的状态未发生改变）；如单质碳有石墨和金刚石两种，O m f G ∆ (298.15K ，石墨，)=0kJmol -1.而O m f G ∆ (298.15K ，金刚石，)=2.9kJmol -1, (课本522页)，石墨到金刚石状态要发生改变，即要发生相变，所以O m f G ∆ (298.15K ，金刚石，)=2.9kJmol -1,不等于零。

2 化合物的标准生成热(焓)定义成：“由稳定单质在298.15K 和100KPaPa 下反应生成1mol 化合物的反应热”是否准确?为什么?答：单独处于各自标准态下，温度为T 的稳定单质生成单独处于标准态下、温度为T 的1mol 化合物B 过程的焓变。

此定义中（1）强调压力为一个标准大气压，而不强调温度；（2）变化前后都单独处于标准态。

所以题中的定义不准确，3 一定温度、压力下，发生单位化学反应过程中系统与环境交换的热Q p 与化学反应摩尔焓变n r H ∆是否相同?为什么?答： 等压不作其他功时（W ’=0），数值上Q p =n r H ∆; Q p 是过程量，与具体的过程有关，而n r H ∆是状态函数与过程无关，对一定的化学反应有固定的数值；如将一个化学反应至于一个绝热系统中Q p 为零，但n r H ∆有确定的数值。

§3.2 化学反应热力学函数改变值的计算. 练习1 O m r G ∆(T ),m r G ∆(T ),Om f G ∆(B ，相态，T )各自的含义是什么?答：Om r G ∆(T )： 温度为T ，压力为P θ，发生单位反应的ΔG;m r G ∆(T ): 温度为T ，压力为P ，发生单位反应的ΔG;Omf G ∆(B ，相态，T ): 温度为T ，压力为P θ，由各自处于标准状态下的稳定单质，生成处于标准态1mol 化合物反应的ΔG;2 25℃时，H 2O(l)及H 2O(g)的标准摩尔生成焓分别为-285.838及-241.825kJ mol -1 。

第三章 化学平衡测试练习题选择题：1、化学反应若严格遵循体系的“摩尔吉布斯函数—反应进度”曲线进行，则该反应在（ A ）[A]．曲线的最低点[B]．最低点与起点或终点之间的某一侧[C]．曲线上的每一点[D]．曲线以外某点进行着热力学可逆过程．2、有一理想气体反应A+B=2C ，在某一定温度下进行，按下列条件之一可以用θm r G ∆直接判断反应方向和限度：（ C ）[A]．任意压力和组成[B]．总压101.325kPa ，物质的量分数31===C B A x x x [C]．总压303.975kPa ，31===C B A x x x [D]．总压405.300kPa ，41==B A x x ，21=C x 3、298K 的理想气体化学反应AB=A+B ，当温度不变，降低总压时，反应的转化率（ A ）[A]．增大 [B]．减小 [C]．不变 [D]．不能确定4、已知气相反应)()(3)(126266g H C g H g H C =+在373K 时的143.192-⋅-=∆mol kJ H mr θ，当反应达平衡时，可采用下列哪组条件，使平衡向右移动（ C ）[A]．升温与加压 [B]．升温与减压[C]．降温与加压 [D]．降温与减压5、化学反应的平衡状态随下列因素当中的哪一个面改变? （ A ）[A]．体系组成 [B]．标准态 [C]．浓度标度[D]．化学反应式中的计量系数νB6、在相同条件下有反应式(1)C B A 2=+，（θ1,m r G ∆）；(2) C B A =+2121，（θ2,m r G ∆）则对应于(1)，(2)两式的标准摩尔吉不斯函数变化以及平衡常数之间的关系为：（ B ）[A]．θθ2,1,2m r m r G G ∆=∆，θθ21K K =[B]．θθ2,1,2m r m r G G ∆=∆，221)(θθK K =[C]．θθ2,1,m r m r G G ∆=∆，221)(θθK K =[D]．θθ2,1,m r m r G G ∆=∆，θθ21K K = 7、反应)()()()(222g H g CO g O H g CO +=+，在600℃、100 kPa 下达到平衡后，将压力增大到5000kPa ，这时各气体的逸度系数为09.12=CO γ，10.12=H γ，23.1=CO γ，77.02=O H γ。

第三章热力学第二定律卡诺热机在的高温热源和的低温热源间工作。

求（1）热机效率；（2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3．2 卡诺热机在的高温热源和的低温热源间工作，求：（1）热机效率；（2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解：(1) 由卡诺循环的热机效率得出（2）3．3 卡诺热机在的高温热源和的低温热源间工作，求（1）热机效率；（2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（1）(2)3．4 试说明：在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时，若令卡诺热机得到的功r W 等于不可逆热机作出的功－W 。

假设不可逆热机的热机效率大于卡诺热机效率，其结果必然是有热量从低温热源流向高温热源，而违反势热力学第二定律的克劳修斯说法。

证： （反证法） 设 r ir ηη>不可逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等，即总的结果是：得自单一低温热源的热，变成了环境作功，违背了热力学第二定律的开尔文说法，同样也就违背了克劳修斯说法。

3．5 高温热源温度，低温热源温度，今有120KJ 的热直接从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程不同的热机中作于的高温热源及的低温热源之间。

求下列三种情况下，当热机从高温热源吸热时，两热源的总熵变。

（1）可逆热机效率。

（2）不可逆热机效率。

（3）不可逆热机效率。

解：设热机向低温热源放热，根据热机效率的定义因此，上面三种过程的总熵变分别为。

已知水的比定压热容。

今有1 kg，10℃的水经下列三种不同过程加热成100 ℃的水，求过程的。

（1）系统与100℃的热源接触。

（2）系统先与55℃的热源接触至热平衡，再与100℃的热源接触。

第三章热力学第二定律卡诺热机在的高温热源和的低温热源间工作。

求（ 1）热机效率；（ 2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3． 2 卡诺热机在的高温热源和的低温热源间工作，求：（ 1）热机效率；（ 2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解： (1) 由卡诺循环的热机效率得出（2）3． 3 卡诺热机在的高温热源和的低温热源间工作，求（ 1）热机效率；（ 2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（ 1）(2)3． 4 试说明：在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时，若令卡诺热机得到的功 W r等于不可逆热机作出的功－W。

假设不可逆热机的热机效率大于卡诺热机效率，其结果必然是有热量从低温热源流向高温热源，而违反势热力学第二定律的克劳修斯说法。

证：（反证法）设η >ηir r不可逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等，即，违背了热总的结果是：得自单一低温热源的热，变成了环境作功力学第二定律的开尔文说法，同样也就违背了克劳修斯说法。

3． 5高温热源温度，低温热源温度，今有120KJ 的热直接从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程不同的热机中作于当热机从高温热源吸热的高温热源及的低温热源之间。

求下列三种情况下，时，两热源的总熵变。

（ 1）可逆热机效率。

（ 2）不可逆热机效率（ 3）不可逆热机效率解：设热机向低温热源放热。

，根据热机效率的定义因此，上面三种过程的总熵变分别为。

已知水的比定压热容。

今有 1 kg，10℃的水经下列三种不同过程加热成100 ℃的水，求过程的。

（1）系统与 100℃的热源接触。

（2）系统先与 55℃的热源接触至热平衡，再与 100℃的热源接触。

第三章热力学第二定律3.1卡诺热机在的高温热源和的低温热源间工作。

求（ 1）热机效率；（ 2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3． 2 卡诺热机在的高温热源和的低温热源间工作，求：（ 1）热机效率；（ 2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解： (1)由卡诺循环的热机效率得出（2）3． 3 卡诺热机在的高温热源和的低温热源间工作，求（ 1）热机效率；（ 2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（1）(2)3． 4 试说明：在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时，若令卡诺热机得到的功 W r等于不可逆热机作出的功－W 。

假设不可逆热机的热机效率大于卡诺热机效率，其结果必然是有热量从低温热源流向高温热源，而违反势热力学第二定律的克劳修斯说法。

证：（反证法）设η >ηir r不可逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等，即总的结果是：得自单一低温热源的热，变成了环境作功，违背了热3． 5 高温热源温度，低温热源温度，今有120KJ的热直接从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程3.6不同的热机中作于的高温热源及的低温热源之间。

求下列三种情况下，当热机从高温热源吸热时，两热源的总熵变。

（ 1）可逆热机效率。

（ 2）不可逆热机效率。

（ 3）不可逆热机效率。

解：设热机向低温热源放热，根据热机效率的定义因此，上面三种过程的总熵变分别为。

3.7已知水的比定压热容。

今有1 kg，10℃的水经下列三种不同过程加热成 100℃的水，求过程的。

（1）系统与 100℃的热源接触。

（2）系统先与 55℃的热源接触至热平衡，再与 100℃的热源接触。

1、1mol 单原子理想气体始态为273K 、p 恒温下压力加倍，计算其Q 、W 、ΔU 、ΔH 、ΔS 、ΔG 、ΔA 。

（已知273K 、p 下该气体的摩尔熵为100J·K -1·mol -1） 解：恒温下压力加倍V nRTP =，当P 1增大P 2时，V 1增大到V 20=∆U0=∆HJ V P Q W 44.4539-=∆-=-=11276.5ln-⋅-==∆K J V V nR S J S T H G 48.1572=∆-∆=∆J S T U A 48.1572=∆-∆=∆2、1mol 理想气体从300K ，100kPa 下等压加热到600K ，求此过程的Q 、W 、ΔU 、ΔH 、ΔS 、ΔA 、ΔG 。

已知此理想气体300K 时的S m =150.0J·K －1·mol －1，C p ,m =30.0J·K －1·mol －1。

解 ： W ＝－p (V 2-V 1) = nR (T 1-T 2) =1×8.314×(300-600) = -2494.2J∆U = nC V ,m (T 2-T 1) =1×(30.00-8.314)×(600-300) = 6506J ∆H = nC p ,m (T 2-T 1) =1×30.00×(600-300) = 9000J Q p = ∆H =9000J∆S = nC p ,m ln(T 2/T 1) =1×30.00×ln(600/300) = 20.79J·K －1·mol －1由 S (600K)=n S m (300K)+∆S =(150.0+20.79) =170.79J·K －1·mol －1∆(TS) =n (T 2S 2－T 1S 1)=1×(600×170.79－300×150.0) ＝57474J ∆G = ∆H －∆(TS) ＝9000－57474=－48474J3、 1mol 理想气体始态为27℃、1MPa ，令其反抗恒定的外压0.2MPa 膨胀到体积为原来的5倍，压力与外压相同。

第三章习题及答案1.试确定在22H ()I (g)g+2HI(g)的平衡系统中的组分数。

（1）反应前只有HI ；（2）反应前有等物质的量的2H 和2I ；（3）反应前有任意量的2H 、2I 及HI 。

解（1）1113'=−−=−−=R R S K （2）1113=−−=K （3）2013=−−=K 4.环己烷在其正常沸点为80.75℃时的气化热为1358J g −⋅。

在此温度是液体和蒸气的密度分别为0.7199和0.00293g cm −⋅。

（1）计算在沸点时d d p/T 的近似值（仅考虑液体体积）；（2）估计在50.510Pa ×时的沸点；（3）欲使环己烷在25℃沸腾，应将压力减压到多少？解（1）根据克拉贝龙方程：6vap m,B m m 31d 358841011d [(g)(l)]353.75840.00290.71992.9510Pa K H p T T V V −⎡⎤⎢⎥∆××⎢⎥==−⎛⎞⎢⎥××−⎜⎟⎢⎥⎝⎠⎣⎦=×⋅若忽略液体体积：6vap m,B 31m d 35884102.9310Pa K 1d (g)353.75840.0029H p T TV −⎡⎤∆⎢⎥××≈==×⋅⎢⎥⎢⎥××⎣⎦(2)由克克方程：vap m,B 211255211ln R 0.5103588411ln 108.314353.75H p p T T T ∆⎛⎞=−⎜⎟⎝⎠⎛⎞××=−⎜⎟⎝⎠解得：2331.29KT =（3）将5211298K,353.75K,10Pa T T p ===代入克克方程得：42 1.4810Pa p =×。

5.溴苯Br H C 56的正常沸点为156.15℃，试计算在373K 时溴苯的蒸气压？与实验值Pa 1088.14×比较并解释这一现象。

第三章 习题解答1. 在298 K 和标准压力下，含甲醇(B)的摩尔分数x B 为0.458的水溶液的密度为0.89463kg dm -⋅，甲醇的偏摩尔体积313(CH OH)39.80 cm mol V -=⋅，试求该水溶液中水的偏摩尔体积2(H O)V 。

解：3322(CH OH)(CH OH)(H O)(H O)V n V n V =+3330.45832(10.458)18()dm 0.02729 dm 0.894610mV ρ⨯+-⨯===⨯ 3313120.027290.45839.8010(H O)() cm mol 16.72 cm mol 10.458V ----⨯⨯=⋅=⋅-2. 298 K 和标准压力下，有一甲醇物质的量分数为0.4的甲醇－水混合物。

如果往大量的此混合物中加入1 mol 水，混合物的体积增加17.35 cm 3；如果往大量的此混合物中加1 mol 甲醇，混合物的体积增加39.01 cm 3。

试计算将0.4 mol 的甲醇和0.6 mol 的水混合时，此混合物的体积为若干？此混合过程中体积的变化为若干？已知298 K 和标准压力下甲醇的密度为0.79113g cm -⋅，水的密度为0.99713g cm -⋅。

解：312(H O)17.35cm mol V -=⋅313(CH OH)39.01 cm mol V -=⋅33322(CH OH)(CH OH)(H O)(H O)26.01 cm V n V n V =+=混合前的体积为：33[(18/0.9971)0.6(32/0.7911)0.4] cm 27.01 cm ⨯+⨯=31.00 cm V ∆=3. 298 K 时，K 2SO 4在水溶液中的偏摩尔体积V B 与其质量摩尔浓度的关系式为：1/2B 32.28018.220.222V m m =++，巳知纯水的摩尔体积V A , m = 17.96 cm 3·mol -1，试求在该溶液中水的偏摩体积与K 2SO 4浓度m 的关系式。