评估中国股票市场的风险预测模型
- 格式:doc
- 大小:27.00 KB
- 文档页数:4

中国证券市场风险分析与VAR模型一、中国证券市场风险分析金融风险是世界各个市场经济国家所面临的共同问题,它不但破坏了一个国家乃至世界经济发展的秩序,而且也直接威胁着一个国家或地区的政治稳定。
从墨西哥金融危机、美国南加州橘县的破产到巴林银行倒闭及日本大和银行的惨重损失都充分地说明了这一点。
金融活动总是存在着金融风险,这是因为人类经济活动中①信息总是不完备、不对称的;②人的理性是有限的。
并且,由于金融领域知识的专门性及技术的复杂性,加之信息传播手段的现代化,金融活动中信息的不完备性及人的有限理性更为突出,这就使得金融活动具有更大的不确定性特征。
但这种较大的不确定性使得金融活动具有较高风险的同时,也具有获得较高收益的可能,即所谓高风险高收益。
从金融业的整体来看,金融业越活跃,越多样化,其不确定性空间也就越大,因而金融业的风险也就越高。
1、中国证券市场风险的总体特征:目前,中国正处于由计划经济体制向市场经济体制转轨的过程之中,旧的体制尚未完全消退,新的体制正在建立,还远不完善。
新旧体制处于相互交错的状态之中。
一方面,旧的计划体制依然在社会经济的许多领域发挥着种种作用,干扰甚至阻碍着新的市场经济体制的建立和运行;另一方面,新的市场经济体制脱胎于旧的计划经济体制,还很不完善,尚不能有效地规范和调节自身的运行,有时还不得不求助于旧的计划经济体制,使得中国证券市场不仅具有成熟证券市场所具有一般风险因素和证券市场发展初期的特殊风险因素,更具有经济转轨时期特有的体制性风险因素,主要表现为:①由于证券市场中的机构投资者利用经济转轨时期法律法规制定和执行过程中存在着的种种不完善,利用新旧体制交替过程中管理方式方法,甚至管理权限中出现的某些真空地带,利用旧体制下形成的权力系统对新体制的合法干预等,人为地操纵市场,兴风作浪,牟取暴利以及“寻租行为造成的证券市场的震荡;②由于管理机构缺乏管理经验而对证券市场干预不及时、不果断或进行不正常干预而造成的证券市场的震荡;③由于相当一部分证券发行企业业绩较差,缺乏对证券价格的业绩支持造成的证券市场基础不牢固所酝酿的潜在风险;④由于中国各行业企业与经济走势之间密切的相关关系所造成的证券市场上很高的系统风险。

股票市场预测模型的研究和应用股票市场是经济中的一个重要组成部分,对于企业和投资者而言,股票市场的走势起伏不仅与公司业绩息息相关,而且还涉及到大量的经济因素,如政策、市场环境等。
因此,对于股票市场的预测一直是金融领域的重要研究方向之一。
股票市场预测模型的定义和分类股票市场预测模型是指用统计学和数学方法,对历史数据进行分析和加工,建立数学模型对未来股票市场价格趋势进行推断和预测的工具。
目前,常用的股票市场预测模型可以分为基于时间序列和基于经济因素两类。
基于时间序列的股票市场预测模型是指根据股票市场历史时间序列数据,建立起股票市场价格的长期、中期、短期趋势和周期变化的预测模型。
常用的模型有ARIMA、ARCH、GARCH、VAR等。
基于经济因素的股票市场预测模型是指从经济层面入手,通过对股票市场诸如宏观经济环境因素、政策因素、公司财务数据等进行分析和综合考虑,预测股票市场价格的变化。
其中包括基本面分析、技术分析、行为金融学等。
股票市场预测模型的应用股票市场预测模型的应用非常广泛,尤其是对于投资者和企业而言,更具有重要的意义。
一方面,股票市场预测模型可以帮助投资者更好地掌握市场变化,及时调整与选择交易策略。
通过对经济、政策、公司等相关因素的综合考虑和分析,可以将投资风险和浮动降至最低。
另一方面,对于企业而言,股票市场预测可以为企业资金筹集和投资决策提供参考和帮助。
企业可以通过对不同市场环境下,不同资本市场价格的预测,根据需要调整投资策略,以尽可能地实现自身利益的最大化。
股票市场预测模型的优势和劣势股票市场预测模型在股票市场分析应用方面有着优势和劣势。
股票市场预测模型的优势在于,它采用了规范化的分析方法,对股票市场历史数据进行了系统分析和整合,能够准确地预测未来可能出现的股票价格走势。
通过对不同时间段的数据进行分析,可以适应不同市场需求和不同投资人的操作需要。
因此,股票市场预测模型能够为投资者和企业提供科学、准确的投资决策依据。

中国股票市场的三因子模型股票市场是一个高风险高收益的金融市场,投资者往往希望通过有效的投资策略来获取良好的回报。
而对于股票市场的投资策略研究,因素模型是一个非常重要的分析工具之一。
本文将讨论,分析其在中国股市中的应用和意义。
首先,我们来了解一下三因子模型的基本概念。
三因子模型是基于CAPM(资本资产定价模型)的改进模型,增加了市场规模因子和价值因子两个额外因子,从而更全面地解释股票回报的变动。
具体来说,这三个因子分别是市场风险因子、市场规模因子和价值因子。
市场风险因子反映了整个市场的风险水平,市场规模因子反映了股票的规模对回报的影响,价值因子反映了投资者对股票价值估计的影响。
三因子模型的核心思想在于,股票回报的变动可以通过这三个因子来解释。
具体而言,市场风险因子影响了所有股票回报的波动,而市场规模因子和价值因子则解释了股票间回报的差异。
对于投资者来说,理解和把握这些因子对股票回报的影响,可以帮助他们制定更加科学的投资策略。
在中国股票市场中,三因子模型的应用具有重要意义。
首先,市场风险因子在中国股市中扮演着至关重要的角色。
由于中国股市的波动性较大,市场风险因子直接影响着股票的回报。
其次,市场规模因子也是中国股市中的重要因素之一。
中国股市中的大盘股往往受到更多投资者的关注,因此市场规模因子对于回报的解释能力也较高。
此外,价值因子也在中国股市中具有重要作用。
由于中国经济快速发展,投资者对于高成长性股票的偏好较大,因此价值因子对于股票回报的影响也相对较大。
然而,需要注意的是,三因子模型也存在一些局限性。
首先,三因子模型是建立在过去的市场数据上的,对于未来的预测能力有限。
其次,三因子模型只考虑了市场风险因子、市场规模因子和价值因子,而忽略了其他可能影响股票回报的因素,如利率、通胀等。
此外,三因子模型在不同市场和不同时间段的适用性也存在差异。
因此在实际应用时,投资者需要结合具体情况进行判断。
综上所述,是一个有效的工具,可以帮助投资者解释和预测股票回报的变动。

股票市场波动的预测模型随着股票市场的日益复杂和波动性的增加,投资者们迫切需要一种准确、可靠的预测模型来帮助他们做出更明智的投资决策。
股票市场的波动不仅仅受到经济因素等基本面因素的影响,还受到市场心理、政治因素等更加复杂的因素的影响。
因此,建立一个全面、有效的股票市场波动预测模型是非常具有挑战性的任务。
首先,我们需要了解股票市场波动的基本特征。
股票市场的波动具有随机性和非线性特征。
传统的线性模型在捕捉波动性方面存在局限性,因此需要采用更加复杂的非线性模型。
非线性模型可以更好地考虑多种因素之间的相互作用关系,提高波动预测的准确性。
一种常见的非线性模型是基于时间序列的支持向量机模型。
该模型利用历史数据来预测未来的波动性。
基于时间序列的支持向量机模型可以捕捉到股票市场的短期和长期依赖关系,并且可以应对非线性和非平稳的数据。
该模型的核心思想是通过将原始数据映射到一个高维特征空间,将非线性问题转化为线性问题,从而实现波动预测。
另一个被广泛使用的非线性模型是基于人工神经网络的模型。
人工神经网络是一种模仿人脑神经元工作方式的计算模型,通过模拟神经元之间的连接和信息传递来对股票市场的波动进行预测。
人工神经网络模型具有很强的非线性拟合能力,可以更好地捕捉数据的复杂关系。
然而,该模型的训练过程较为复杂,需要大量的历史数据和计算资源。
除了上述两种模型之外,还有一种基于复杂系统理论的模型,即混沌理论。
混沌理论认为股票市场的波动是由于多种非线性和非确定性因素的相互作用而形成的。
混沌理论可以通过分析市场中的复杂动力学系统来预测股票市场的波动。
然而,混沌理论的应用范围有限,需要大量的数据和数学方法。
除了这些传统模型,近年来,机器学习和人工智能技术的兴起为股票市场波动预测提供了新的思路和方法。
机器学习模型可以通过大量的历史数据进行训练,并根据模型的学习能力自动调整参数,以改善波动预测的准确性。
其中一种常用的模型是随机森林模型,它基于决策树的集成学习方法,能够处理高维数据、缺失数据和非线性关系。

我国A股市场CAPM模型和Fama-French三因子模型的检验我国A股市场CAPM模型和Fama-French三因子模型的检验引言:资本资产定价模型(CAPM)和Fama-French三因子模型是金融学中两个经典的资产定价模型。
本文旨在对我国A股市场中的CAPM模型和Fama-French三因子模型进行检验和分析,以探讨这两种模型在我国A股市场的适用性和效果。
一、CAPM模型CAPM模型是由美国学者Sharp、Lintner、Mossin等人在20世纪60年代提出的,并在随后的几十年里成为基金、股票和其他金融衍生品定价的重要工具。
其基本假设是市场上的风险资产回报与其风险高低成正比。
CAPM模型的表达式为:E(Ri) = Rf + βi[E(Rm) - Rf]其中,E(Ri)为资产的预期回报;E(Rm)为市场的预期回报;Rf为无风险资产的回报率;βi为资产i的系统性风险。
对于我国A股市场,CAPM模型的检验有两个关键问题:一是如何计算无风险收益率(Rf);二是如何估计资产的beta 值。
关于无风险收益率(Rf)的计算,有三种常用的方法:国债收益率法、货币市场基金收益率法、银行存款利率法。
由于我国国债市场的不完善,货币市场基金收益率与银行存款利率相对稳定,因此可采用货币市场基金收益率作为无风险收益率进行计算。
对于资产的beta值的估计,通常采用历史回归法。
通过回归资产收益率与市场收益率的历史数据,可以得到资产的beta值。
然而,由于我国A股市场的特殊性,投资者行为和政策因素对资产收益率的影响较大,使用历史回归法估计的beta值可能存在较大的误差。
二、Fama-French三因子模型Fama-French三因子模型是由美国学者Eugene Fama和Kenneth French在上世纪90年代提出的,其基本假设是资产的回报与市场风险、规模风险和价值风险三个因素有关。
Fama-French三因子模型的表达式为:E(Ri) = Rf + βi1(E(Rm) - Rf) + βi2(SMB) + βi3(HML)其中,E(Ri)为资产的预期回报;Rf为无风险收益率;βi1为资产与市场收益的相关系数;βi2为资产与规模因子(市值大小)的相关系数;βi3为资产与价值因子(公司估值)的相关系数;SMB为规模因子的收益率;HML为价值因子的收益率。

基于VAR模型的股票市场波动风险评估股票市场对于投资者来说是一个充满机会和风险的领域。
没有人可以准确预测股票市场的走势,但是我们可以通过对市场变化的研究和分析,来评估市场的波动风险。
其中一种方法就是利用VAR模型来进行风险评估。
1. 什么是VAR模型?VAR模型是一种广泛应用于金融领域的统计模型,它可以分析多个变量之间的关系和相互作用,从而预测未来的市场走势和波动。
VAR模型的核心是矩阵代数,通过对多个变量的观测值进行线性组合,得出它们之间的相关性和因果关系。
2. VAR模型在股票市场中的应用在股票市场中,VAR模型通常用于评估风险和波动性。
以某个股票为例,我们可以通过收集多个相关变量的数据,如股价、成交量、市值、财务指标等,建立一个VAR模型,来预测未来的股价走势和波动。
VAR模型的一个重要输出结果是价值-at-风险(VaR)指标。
VaR是指在一定置信水平下,某个投资组合或资产在一定时间内可能面临的最大损失。
例如,我们可以预测某个股票在5个交易日内的VaR为10%,这意味着在95%的置信水平下,该股票在未来5个交易日内最多会下跌10%。
3. 如何建立VAR模型?建立VAR模型的关键在于选择合适的变量和时间段。
一般来说,需要选择与特定股票相关的多种指标,并收集相应的历史数据。
例如,对于某家公司的股票,我们可以选择该公司的财务数据、行业指标、市场数据等。
同时,需要考虑时间段的选择,一般来说,需要选取足够长的时间段来覆盖多个市场情况和周期性变化。
建立VAR模型后,我们可以通过模型的输出结果来评估股票市场的风险和波动性。
例如,我们可以预测一只股票在未来三个月内的VaR为8%,这意味着在95%的置信水平下,该股票在接下来的三个月内最多会下跌8%。
4. VAR模型的局限性尽管VAR模型在股票市场中广泛应用,但它也存在一定的局限性。
首先,VAR模型假设变量之间是线性的,并且假设变量之间的相关性是稳定的。
然而,在现实中,经济变量之间的关系往往是非线性的,并且可能因为外部因素的影响而发生变化,这会影响VAR模型的预测准确性。

基于GARCH模型的我国股市风险分析
股市风险是指股票价格的波动性和不确定性,投资者在股市中面临的风险。
风险分析对于投资者合理评估风险并做出投资决策至关重要。
基于GARCH模型的股市风险分析是一种常用的方法,它可以通过对股票价格波动的建模来预测未来的股票价格波动情况。
GARCH模型是基于ARCH模型(自回归条件异方差模型)的扩展,主要用于描述时间序列的波动,并不仅仅限于股市。
GARCH模型包含一个条件异方差项,用来捕捉股票价格波动的自相关特征。
通过对股票价格历史数据进行建模分析,可以估计出模型中的参数,并预测未来的股票价格波动。
我国股市风险分析可以基于GARCH模型进行。
需要收集股票价格的历史数据,通常包括每日的收盘价或每周的收盘价。
然后,根据历史数据计算出股票价格的波动率,作为GARCH模型的输入变量。
接下来,使用最大似然估计方法估计模型的参数,并进行模型拟合。
利用估计的模型,可以进行未来股票价格波动的预测和风险分析。
GARCH模型的输出结果包括条件异方差项的系数和波动率的预测。
系数可以用来判断股票价格波动的自相关特征,以及预测未来的波动模式。
波动率的预测可以反映出未来股票价格的波动情况,进而帮助投资者评估股市的风险。
除了基于GARCH模型的股市风险分析,还可以结合其他方法进行综合分析。
可以结合股票价格的历史数据和基本面分析,来评估股市的风险。
基本面分析包括公司财务状况、市场竞争状况等因素的考虑,可以提供更全面的风险评估。

股票市场预测模型分析一、背景:在当今社会,股票市场已经成为了投资者最为关注的一个话题。
而能够有效提高股票交易成功率的预测模型分析,也备受人们的重视。
因此,本文将对当前最为流行的股票市场预测模型进行详细分析,以期为广大投资者提供参考。
二、基础知识:1.股票市场:股票市场是指以股票为交易对象的市场,它是通过买卖股票来进行盈利的主要场所。
股票交易是投资人们进行投资的主要方式之一。
2.预测模型:预测模型是指对未来某种变量或某种现象进行预测的一种数学模型。
预测模型能够通过对历史数据进行分析和预测来帮助投资者预估市场走向和风险等因素。
三、股票市场预测模型分析:1.趋势模型:趋势模型也叫做趋势线模型。
这种模型是股票分析中最为常见的模型之一,其核心是通过绘制趋势线来预测市场走势。
具体而言,趋势模型会首先根据历史数据绘制一条趋势线,然后根据该趋势线推断未来市场走势。
趋势模型是一个较为简单的模型,应用范围也比较广泛,是股票分析中不可缺少的模型之一。
2.周期模型:周期模型也称为周期指标。
这种模型主要通过对市场走势进行长期观察,来找寻市场中的规律性周期变动。
周期模型认为市场走势是由多种周期波动叠加而成的,而通过对这些波动进行分析,就能够帮助投资者预测市场未来的波动情况。
周期模型的核心是“周期”概念,也是其最为重要的理论基础。
3.回归模型:回归模型也称多元线性回归模型。
这种模型主要通过对市场数据进行线性回归分析,来找出市场中的“影响因素”,从而预测市场走势和变化趋势。
回归模型中最为重要的指标是“R²值”,它可以用来反映市场中各个因素对市场走势的影响程度。
而通过对这些因素进行分析,就可以帮助投资者对市场进行更为准确的预测和分析。
4.随机漫步模型:随机漫步模型也叫随机行走模型。
这种模型主要基于股票市场的随机性和随机漫步理论,从而预测市场的走势。
随机漫步模型的核心是在统计上发现市场不具备长期趋势性,并且未来市场的变化是有不确定性的。

股票市场风险评估模型的构建与应用1. 导言股票市场风险评估是投资者决策的重要依据之一。
构建有效的风险评估模型可以帮助投资者更好地理解市场风险,并做出相应的投资决策。
本文将介绍股票市场风险评估模型的构建与应用。
2. 风险定义与分类在构建风险评估模型之前,首先需要明确风险的定义与分类。
风险可定义为投资者在获得预期回报的同时,面临的不确定性和潜在损失的可能性。
根据风险来源的不同,可以将风险分为系统性风险和非系统性风险。
系统性风险是与整个市场相关的风险,例如宏观经济风险、政策风险等;非系统性风险则是与特定企业相关的风险,如行业竞争风险、管理风险等。
3. 构建风险评估模型的方法构建风险评估模型的方法有很多种,以下将介绍两种常见的方法。
3.1 基于历史数据的风险评估模型基于历史数据的风险评估模型通过分析历史市场数据,寻找股票的风险特征和规律,来评估市场风险。
常见的方法包括方差-协方差模型、VaR模型等。
方差-协方差模型假设市场收益服从正态分布,并通过计算股票回报的方差和协方差矩阵来评估风险。
VaR模型则是通过计算在一定置信水平下的最大可能损失来评估风险。
这些方法在构建风险评估模型时需要考虑数据的准确性和代表性,以及对分布假设的合理性进行验证。
3.2 基于评分模型的风险评估模型基于评分模型的风险评估模型是通过构建评分卡来评估股票的风险水平。
评分卡包括多个指标,通过对这些指标进行加权计算,得到一个综合的风险评分。
指标的选择可以根据实际情况进行确定,常见的指标包括市盈率、市净率、负债比率等。
在确定权重时,可以采用专家判断、主观评估以及数据挖掘等方法。
4. 风险评估模型的应用风险评估模型在股票市场中有着广泛的应用,以下将介绍两个应用案例。
4.1 投资组合优化风险评估模型可以用于投资组合的优化,帮助投资者选择合适的资产组合。
投资组合的风险评估可以通过计算组合的方差、协方差矩阵以及VaR等指标进行。
通过优化投资组合的权重分配,可以最大程度地减少投资组合的风险。

基于GARCH模型的我国股市风险分析随着我国经济的不断发展,股票市场作为重要的资本市场之一,一直受到投资者的关注。
股票市场存在着各种各样的风险,投资者需要对市场风险进行深入的分析和研究。
本文将基于GARCH模型,对我国股市的风险进行分析,并探讨其影响因素和预测方法。
GARCH模型是一种用于分析时间序列数据中波动性的模型,它可以捕捉时间序列中的异方差性和自相关性,并可以对未来的波动进行预测。
在股票市场的风险分析中,GARCH模型可以用来对股价波动的风险进行建模和预测,为投资者提供决策依据。
我们来分析我国股市的波动性。
我国股市的波动性普遍较高,由于市场面临着包括政治、经济、金融等多方面的风险,股价波动十分剧烈。
以沪深300指数为例,我们可以利用GARCH模型对其波动性进行分析。
通过对历史数据的分析,我们可以得到沪深300指数的波动性指标,并利用GARCH模型进行波动性预测。
这有助于投资者更好地了解市场风险,进行风险管理和决策。
我们来探讨影响我国股市风险的因素。
我国股市风险受多方面因素的影响,包括宏观经济、政策、市场情绪等因素。
宏观经济因素如经济增长、通货膨胀、利率等对股市波动有着重要影响。
政策因素包括政府政策、监管政策等,这些因素往往会对市场产生重大影响。
市场情绪也是影响股市波动的重要因素,投资者情绪的波动会直接影响股市的波动性。
通过对这些影响因素的分析,可以更全面地理解我国股市风险的来源,为投资者提供基于风险的投资建议。
我们来探讨基于GARCH模型的我国股市风险预测方法。
利用GARCH模型可以对股市波动性进行预测,为投资者提供风险管理和决策依据。
通过对历史数据的建模和预测,可以得到未来股市波动性的预测值,帮助投资者更好地掌握市场风险,进行风险管理和决策。
还可以利用GARCH模型进行蒙特卡洛模拟、价值-at-risk(VaR)计算等方法,进一步提高风险预测的准确性和可靠性。
基于GARCH模型的我国股市风险分析是一项重要的研究课题,有助于投资者更全面地了解市场风险,进行风险管理和决策。
基于GARCH模型的我国股市风险分析摘要:本文针对我国股市风险建立了基于GARCH模型的风险分析模型。
首先,利用ADF检验和KPSS检验对数据进行平稳性检验,然后使用对数收益率序列来对股市进行分析,进而建立GARCH模型,并通过对历史数据拟合模型来得到模型所需的参数。
最后,通过计算模型的VaR和CVaR来测算股市风险,并且以实际数据为例进行验证,结果表明该模型可以有效地评估我国股市的风险,并为投资者提供决策支持,降低投资风险。
关键词:GARCH模型;股市风险;VaR;CVaRAbstract:In this paper, a risk analysis model based on GARCH model is established for China's stock market. Firstly, ADF test and KPSS test are used to test the stationarity of the data. Then, the logarithmic return sequence is used to analyze the stock market, and the GARCH model is established. Finally, the VaR and CVaR of the model are calculated to measure the risk of the stock market, and the model is verified by using actual data. The results show that the model can effectively evaluate the risk of China's stock market and provide decision support for investors to reduce investment risk.Keywords: GARCH model; stock market risk; VaR; CVaR1. 引言股市风险一直是金融领域的热点问题之一,而对股市风险进行评估和控制也是投资者必须面对的问题之一。
基于GARCH模型的我国股市风险分析
本文将基于GARCH模型,对我国股市风险进行分析。
GARCH模型是一种用来分析时间序列中波动性的模型,包括了自回归模型和移动平均模型的特征。
通过对我国股市的历史数据进行分析,研究股市风险和波动性的变化趋势,以及可能产生的影响。
首先,我们根据股市指数数据,对我国股市的风险性进行分析。
在过去的20年里,我国股市的风险性呈现出波动性上升的趋势,特别是2008年和2020年,股市风险出现较大的波动,这表明我国股市的波动性有逐渐增加的趋势。
接着,我们使用GARCH模型来分析我国股市的波动性。
我们采用的GARCH模型为GARCH(1,1),其中1表示自回归项,1表示移动平均项。
我们使用的数据是上证综指的收盘价数据。
根据GARCH(1,1)模型的拟合结果,我们可以发现我国股市确实存在着波动性。
拟合出的波动性参数是0.087,这意味着标准差在5天内预测的误差率为8.7%。
同时,我们也可以发现,GARCH模型能够很好地描述我国股市的波动性和风险性,其拟合结果非常符合实际数据。
最后,我们通过对GARCH模型的拟合结果进行预测分析,分析了我国股市未来的波动趋势。
根据GARCH模型预测,未来一年内,我国股市的波动性可能还会有所增加,但总的来说,股市的波动性和风险程度会逐渐趋于平稳。
这意味着,未来的股市风险不会再出现过去那样的大幅波动。
总的来说,基于GARCH模型的分析,我们可以得出结论,我国股市的风险和波动性呈现出逐渐增加的趋势,但总的来说未来趋势将逐渐平稳。
通过对股市风险的深入研究,可以更好地帮助投资者进行风险管理和投资决策。
股票投资风险评估模型探讨股票投资是一种风险高收益高的投资方式,因此需要评估股票投资的风险,以便投资者能够更好地管理自己的资产。
本文将围绕股票投资风险评估模型展开探讨,帮助投资者更好地评估股票投资的风险和收益。
一、股票投资的风险股票投资是一种高风险的投资方式,因为股票市场的波动性较大,股票价格随时可能发生剧烈变化。
股票投资的风险主要包括以下几个方面:1.市场风险:市场风险是指由于各种经济、政治、社会等因素对整个市场的影响而导致的投资风险。
例如,宏观经济、政策法规、自然灾害等都会对市场产生影响,从而导致股票价格的波动。
2.行业风险:行业风险是指由于不同行业的内部因素所带来的投资风险。
不同行业的运作环境不同,行业的竞争程度、产品生命周期、技术创新等都会对企业的发展产生影响,从而导致股票价格的波动。
3.公司风险:公司风险是指由于某些公司的内部因素所带来的投资风险。
例如,公司管理层的不慎决策、财务管理不善、失误等都会导致公司业绩下滑,从而影响股票价格。
二、股票投资风险评估模型为了准确评估股票投资的风险,通常采用一些评估模型来辅助分析。
常见的股票投资风险评估模型有以下几种:1.贝塔系数模型:贝塔系数模型是一种反映股票波动性和市场波动性之间关系的模型。
它将股票与市场进行比较,计算股票收益与市场收益之间的相关性。
贝塔系数越高,表明股票的波动性越大,风险越高。
2.风险价值模型:风险价值模型是一种基于风险价值概念的风险评估模型。
它通过计算股票的价值变化情况来评估股票的风险,可以反映出股票价格波动的可能范围,帮助投资者更好地制定风险控制策略。
3.历史模拟模型:历史模拟模型是一种基于历史数据的风险评估模型,它通过分析过去一段时间内股票的价格变化情况,来预测未来股票价格的变化趋势,帮助投资者更好地制定投资策略。
三、如何选择适合自己的风险评估模型在选择适合自己的风险评估模型时,需要考虑以下几个因素:1.投资者个人偏好:不同的投资者对风险的承受能力和投资风格不同,需要选择符合自身偏好的风险评估模型。
投资风险评估模型及其在股票市场中的应用在金融市场中,投资者总是希望能够获得最大的回报,但开展投资活动时也难以避免的面临了投资的风险,如何在风险和回报之间做出权衡是投资活动中的重要问题。
为此,投资者需要对风险进行科学评估,在评估的基础上,制定科学合理的投资策略,对投资风险进行控制。
而投资风险评估模型就是评估风险的一种工具,它可以在一定程度上为投资者提供帮助。
投资风险评估模型是指通过对投资标的的分析和研究,结合相关的风险指标,对投资过程中可能发生的不确定性因素进行量化和分析,从而得到投资风险的评估结果。
根据所使用的风险指标不同,投资风险评估模型可以分为多种类型,包括历史模型、正态模型、文化模型、风险价值模型等等,其中最为常用的是风险价值模型。
风险价值模型(Value at Risk,VaR)是在一定概率水平下,研究投资组合或资产价格可能出现的最大损失的方法。
VaR模型实质上是一个风险限制模型,即为了控制投资风险,投资者需要在特定概率水平下,限制投资组合或资产价格的最大损失,例如95%的概率下投资组合的最大损失不超过1%。
因此VaR模型能够为投资者提供一个可接受的风险水平,帮助投资者制定具体的投资策略。
在股票市场中,投资者面临的风险复杂多样,包括市场风险、价格波动风险、操作风险、信用风险等等。
其中市场风险是指由于整个市场环境的不确定性而导致的风险,价格波动风险是指由于价格的波动而导致的风险,操作风险是指由于操作错误或疏忽而导致的风险,信用风险是指由于债务人无法按时履行债务而导致的风险。
这些风险因素相互作用,可能会对投资造成影响。
在此背景下,VaR模型作为一种风险评估模型,可以被用于股票市场中的投资风险控制。
在使用VaR模型对股票市场中的投资风险进行评估时,投资者需要考虑多个因素。
首先是股票价格的波动情况。
股票价格的波动程度越大,所承担的风险也就越高。
因此,投资者需要通过历史价格数据或预测模型等方式,预测股票价格的波动情况,根据预测结果计算出VaR值。
股票市场预测与决策的数学模型研究股票市场一直以来都是高风险高收益的投资领域。
投资者希望通过对市场发展的预测来做出正确的决策,从而获取最大化的收益。
然而,在一个不断变化的市场中,想要准确预测并不容易。
数学模型便可以为投资者提供一种较为可靠的预测分析工具,而且还可以辅助投资者做出最优决策。
一、时间序列模型时间序列模型是一种重要的数学模型,主要用于预测未来的股票价格。
这种模型是依据股票市场在时间上的连续性,将历史上不同时间点的价格数据作为自变量,预测未来价格的变化走势。
时间序列模型的核心思想是根据历史数据的规律性和周期性,来推测未来的价格变化。
这种模型主要分为自回归模型、滑动平均模型以及ARIMA模型三种。
其中,自回归模型(Autoregressive Model,AR)是根据历史数据的规律性来对股票未来的价格进行预测的。
其基本思想是,将过去若干期的股票价格作为自变量,对未来的股票价格进行预测。
这个模型的优点在于简单易懂,但缺点也很明显,只能预测一定时间内的价格走势。
滑动平均模型(Moving Average,MA)是根据历史数据的周期性来对未来股票价格进行预测的。
其基本思想是,用过去若干期的股票平均价格来预测未来的价格变化。
这个模型在预测长期股票价格时效果较好,但在短期预测上则表现较差。
ARIMA模型则将自回归模型和滑动平均模型结合起来,既考虑规律性,又考虑周期性。
ARIMA模型适合预测短期和长期股票价格。
二、神经网络模型神经网络模型是一种人工智能模型,通过对股票市场的历史数据进行学习,得出未来股票价格变化的预测结果。
这种模型是基于大量数据的学习和模式识别,可以对股票价格变化的非线性关系进行预测。
神经网络模型的核心思想是,将股票市场的历史上升和下降的趋势当做股票价格变化的非线性模型进行学习,通过训练,得出一个适用于未来的预测模型。
这种模型可以自适应地进行调整,使得其能够在不同时期对股票价格变化进行预测。
市场经济中的市场风险评估模型
市场风险评估是市场经济中一项十分重要的工作,通过评估市场的风险水平可以帮助投资者和企业制定合理的投资策略和风险管理措施。
在市场经济中,市场风险评估模型起着至关重要的作用。
1. 随机游走模型
随机游走模型是市场风险评估中最基本的模型之一,它假设市场价格的变动是随机的,并且未来的价格变动不受过去价格的影响。
这种模型主要运用于对证券市场的长期趋势进行评估。
2. 波动率模型
波动率模型是一种常用的市场风险评估模型,它通过对资产价格波动的测量和预测来评估市场风险。
波动率模型可以帮助投资者更好地把握市场波动的情况,从而制定更为准确的投资策略。
3. 历史模拟模型
历史模拟模型是一种基于历史数据进行市场风险评估的方法,通过对历史市场数据进行统计分析,可以评估市场在未来一段时间内的风险水平。
这种模型主要关注市场过去的表现,以此来预测未来的风险情况。
4. 蒙特卡洛模拟
蒙特卡洛模拟是一种常用的市场风险评估方法,通过随机生成大量的市场情景,综合考虑各种可能性,从而评估市场在不同情况下的风险水平。
这种模拟方法可以更为全面地评估市场风险,有助于投资者做出更为准确的决策。
市场经济中的市场风险评估模型是搭建在大量经济学理论和数学模型基础之上的,各种模型都有其特定的适用范围和局限性。
在实际应用中,投资者和企业需要根据自身的风险承受能力和投资目标,选择合适的市场风险评估模型,从而更好地管理和规避市场风险,实现自身的投资目标。
评估中国股票市场的风险预测模型
摘要对中国股票市场的风险价值(VaR)模型的预测能力进行评估,现存着很多种VaR模型。
这里我们仅对方差-协方差法进行研究。
把它应用在中国股票市场指数上(2000.5.08-2005.4.29),然后对2003.5.12-2005.4.29的数据,根据Christoffersen检测法评价它们的预测结果。
关键词VaR;方差-协方差法;指数;收益;分位数,Christoffersen检测法
近二十年来,由于受经济全球化与金融一体化、现代金融理论及信息技术、金融创新等因素的影响,全球金融市场迅猛发展。
金融市场呈现出前所未有的波动性,工商企业、金融机构正面临着日趋严重的金融风险。
金融风险不仅严重影响了工商企业和金融机构的正常运营和生存,而且还对一国乃至全球金融及经济的稳定发展构成了严重威胁。
近年来频繁发生的金融危机造成的严重后果充分说明了这一点。
因此,风险管理的理论与实践也因此在最近十年得到了迅猛发展,越来越多的公司和企业引入了风险管理,很多著名商学院都已把它作为金融学的一个独立分支。
在这里要对中国股票市场的风险价值(VaR)模型的预测能力进行评价。
1VaR
1.1VaR的定义
VaR是Value at Risk 的缩写,是指在市场正常波动范围内和给定的置信水平下,某一特定的金融资产或证券组合A在给定的持有期内预期可能发生的最大损失。
可表示为:
其中,表示证券组合在持有期内的回报。
上式表明,在持有期内该证券组合的回报低于的概率为。
1.2对VaR计算方法的简要介绍
从VaR的定义,我们不难看出,VaR实际上就是投资组合收益分布的一个分位数。
计算VaR的方法大致可分为以下四种:
1)历史模拟法(Historical Simulation);
2)蒙特卡罗模拟法(Monte Carlo Simulation);
3)建立在极值理论基础上的VaR方法(the EVT-based VaR method);
4)方差—协方差法(Variance-covariance methods)。
由于前三种在技术上较为复杂,较难实现,因此,在实践中常用的方法是方差——协方差法。
这种方法是最标准的方法。
在这篇文章里,因为我们考虑单一的股票指数来代替一组投资,所以我们不用考虑协方差,因此,它也可以被称作方差法。
在这种方法中,可以通过以下公式估计出:
因此,估计VaR涉及到估计,和。
我们考虑各种估计VaR的方法,它们可能应用不同的方法估计和。
这里有两个需要注意的问题。
一是如何刻画金融数据的尖峰厚尾、波动簇集的时变特征;二是如何寻找金融数据的分布密度函数。
这里我们可以假设服从一定的参数分布(例如正态分布)或者应用一些无参数估计。
条件分布被假定为一直保持不变或者简单的认为服从高斯分布
N(0,1),在这里和。
条件方差可以通过各种发散性的方法进行估计,例如简单移动均值模型(亚历山大,1998),指数权重移动均值风险测度模型(EWMA)和Engle(1998),Bollerslev(1986),Nelson(1991)和Glosten et al.(1993)的ARCH模型。
计算VaR最简单的方法就是用历史移动均值方差法来估计资产盈利的发散性。
在这种方法中,我们估计发散性
其中。
看亚历山大(1998)了解依赖经验的优点和缺点。
这种方法将被记为MA(m)。
在我们的经验部分,我们使用MA(200)。
在风险管理框架中最受欢迎的发散模型是摩根的风险测度(1995),它是一种IGARCH方法,详述过程如下:
其中。
风险测度法假设一个固定的,它实质上减少了发散性的计算。
这种方法我们将记为RM()。
通过经验的分析,我们考虑使用RM(0.94),RM(0.97)和RM(0.90)。
2对中国股票市场的预测
我们评估上面模型的预测能力,首先使用中国股票市场上的上证指数2000.5.08-2005.4.29的数据,然后对2003.5.12-2005.4.29的数据进行预测。
这里=0.01或0.05,要用四个模型进行预测,所以要得出八组数据,每组数据共474个预测值。
由于数据太多的缘故,我们不把所有模型预测出的数据一一列在正文中,而是直接用Christoffersen检测法对VaR的预测值进行评估。
2.1Christoffersen检测法
在这里我们介绍三种Christoffersen的可能性比例检测法。
首先定义为模型的数目(k=1,…,)去和基准点模型(k=0)进行比较。
我们再定义指针,t=R,……,T,用来记录当盈利超出第k个模型估计出的预测值时的情况。
这种无条件的概率可以记为。
这个指针{}存在一个二项分布,它是,其中以及分别是指针序列中0和1的数目。
注意。
在中的指数和通常通过下面的部分被抑制。
首先,我们要检测它是否符合上面的无条件概率等于。
相当于假设检验。
指针的二项分布,如果理想状态,,因此可能性比例测试统计量是:
其中是的最大可能性统计量。
第二种测试是用来检验过程是否是序列的独立的。
如果一阶的Markov链可能性变换被表述为,那么独立的可能性比例可以通过下式进行检验
其中
其中表示数值i后紧跟的是数值j的观察值的数目,。
结合这两种检测法,第三种条件范围测试可以被描述成:
2.2对预测的检测
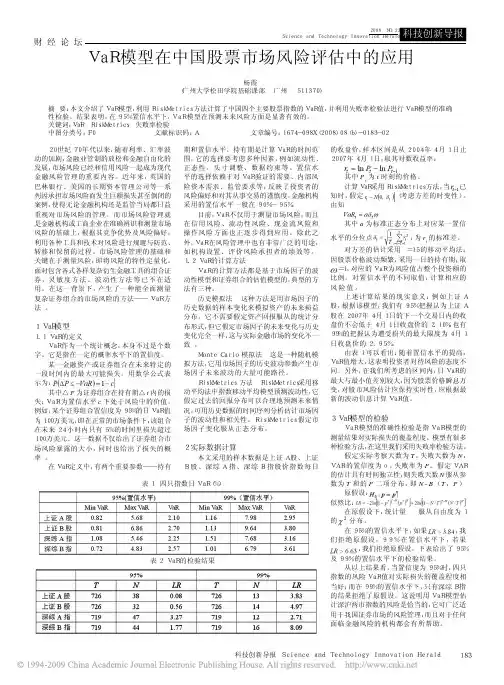
我们利用Christoffersen检测法,对上面的数据进行处理,得到表1。
在这里我们设R=720,P=474,把预测值与真实值(2003.5.12-2005.4.29)进行比较得出以上数据。
当选时,查分布上侧分位数表,得,;当选时,查分布上侧分位数表,得,。
很显然,都小于它们的边界值,符合分布的要求。
3分析与结论
这里我们并没有检测模型在经济危机时期的预测能力,也没有比较这些模型之间的优劣。
我们只是采用Christoffersen检测法,大致的了解一下模型MA(200),RM(0.94),RM(0.97),RM(0.90)的常规预测能力。
从表1我们可以看出,由四个模型估测出的值都很接近真实的范围。
说明RM 模型和MA模型在平常时期,也就是非危机时期,能够起到很好的预测作用。
参考文献
[1]周概容.概率论与数理统计[M].高等教育出版社,1987.
[2]斯蒂芬A·罗斯,伦道夫W·威斯特菲尔德,杰弗利F·杰弗.吴世农,沈艺峰,王志强.等译.公司理财[M].机械工业出版社,2003.
[3]李凤霞,刘桂山,陈朔鹰,薛庆.C语言程序设计教程[M].北京理工大学出版社,2001.
[4]Abberger,K,1997.Quantile smoothing in financial time series .Statistical Papers 38,125-148.
[5]Christoffersen,P.F.,1998.Evaluating interval forecasts. International Economic Review 39(4),841-864.。