简单的轴对称图形等腰三角形

《简单的轴对称图形——等腰三角形》教学设计【教材分析】《简单的轴对称图形——等腰三角形》是初二上册第二章第3小节的内容，是在学生掌握了轴对称图形的知识基础上进行学习的。

本节课意在通过让学生动手操作折叠等腰三角形和等边三角形来发现等腰三角形和等边三角形的性质，从而培养学生动手操作能力和独立发现问题的能力。

本节课的重点是通过折叠图形探究等腰三角形的性质。

而“等边对等角”和“三线合一”的性质是今后论证两个角相等、两条线段相等、两条直线垂直的重要依据。

同时通过这节课的学习还可培养学生的动手、动脑、动口、合作交流等能力。

加强学生对直觉、猜想、演绎、类比、归纳、转化等数学思想、方法的领会掌握，培养学生的探究能力和创新精神。

【学情分析】初二学生思维活跃、愿意表达自己的见解，具有一定的独立思考、实践操作、合作交流、归纳概括的能力。

因此，在本节课的教学中，可让学生从已有的生活经验出发，参与知识的产生过程，在实践操作、自主探索、思考讨论、合作交流等数学活动中，理解和掌握数学知识和技能。

另外学生的思维逐渐由形象思维向抽象思维转变,但形象思维仍占主导地位,数形结合是学生掌握知识的较好方法。

【教学目标】1.知识技能①熟悉等腰三角形、等边三角形是轴对称图形。

②掌握等腰三角形的性质以及简单地应用；等边三角形的性质。

③熟练运用等腰三角形的性质解决等腰三角形内角的计算问题。

2.数学思考①通过折叠等腰三角形发展其形象思维。

②通过动手操作、观察、思考，积累数学活动经验，感受数学思考过程的条理性。

3.解决问题①通过问题的探索过程，体会数学来源于生活。

②会用符号语言表示等腰三角形的性质，发展学生运用符号语言表述问题的能力。

4.情感态度①在数学活动中获得成功体验，培养学生动手操作，勇于探索的精神。

②通过学生之间的交流活动，培养学生主动与他人合作交流的意识。

【教学重点】探索等腰三角形的性质，能够利用等腰三角形的知识解决相应的数学问题。

【教学难点】等腰三角形性质的探究和应用。

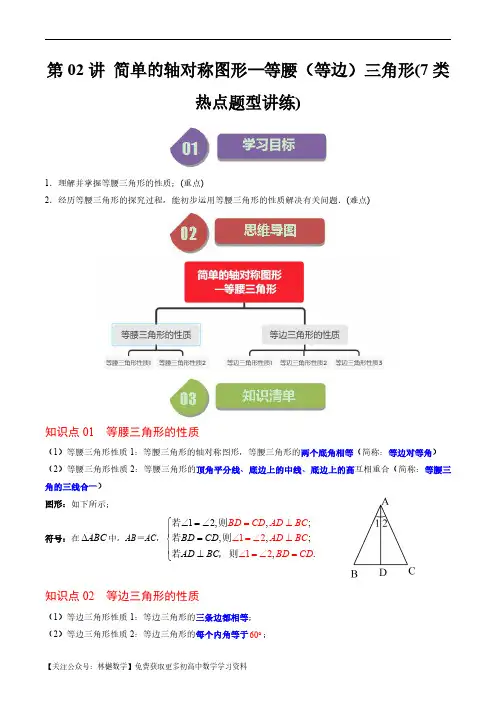
第02讲简单的轴对称图形—等腰（等边）三角形(7类热点题型讲练)1．理解并掌握等腰三角形的性质；(重点)2．经历等腰三角形的探究过程，能初步运用等腰三角形的性质解决有关问题．(难点)知识点01等腰三角形的性质（1）等腰三角形性质1：等腰三角形的轴对称图形，等腰三角形的两个底角相等（简称：等边对等角）（2）等腰三角形性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（简称：等腰三角的三线合一）图形：如下所示；符号：在ABC ∆中，AB ＝AC ，1212,,;,,;,12.BD CD AD BC AD B BD CD AD BC C BD CD ∠=∠⎧⎪=⊥∠=∠⊥∠=∠⎨⎪⊥⎩==若则若则若，则知识点02等边三角形的性质（1）等边三角形性质1：等边三角形的三条边都相等；（2）等边三角形性质2：等边三角形的每个内角等于60︒；（3）等边三角形性质3：等边三角形是轴对称图形，有三条对称轴.题型01等腰三角形两腰相等求解【例题】（23-24八年级上·浙江宁波·期中）若a ，b 为等腰ABC 的两边，且满足()240a -=，则ABC的周长为（）A ．16B ．18C ．20D ．16或20【变式训练】1．（22-23八年级上·湖南岳阳·期中）等腰三角形的两边长分别是3cm 和7cm ，则该三角形周长为．2．（22-23七年级下·陕西西安·阶段练习）定义；等腰三角形的底边长与其腰长的比值k 称为这个等腰三角形的“优美比”．若等腰三角形的周长为13cm ，5cm AB =，则它的“优美比”k 为（）A ．54B ．35C ．54或35D ．45或53题型02根据等边对等角求角度【例题】（23-24八年级上·浙江绍兴·期末）如图，在ABC 中，AB AC =，110ACD ∠=︒，则B ∠=．【变式训练】1．（2024·北京·一模）如图，已知等腰三角形ABC ，AB AC =，40A ∠=︒，若以点B 为圆心，BC 长为半径画弧，则ABE ∠=°．2．（23-24八年级下·云南文山·阶段练习）如图，已知AB AC =，CD CE =，EF EG =，60A ∠=︒，求G ∠的度数为°．题型03根据等边对等角证明【例题】（2023·吉林长春·模拟预测）如图，ABC 是等腰三角形，点D ，E 分别在腰AC ，AB 上，且BE CD =，连接BD ，CE ．求证：BD CE =．【变式训练】1．（2024·江苏南京·一模）如图，在ADE V 和FDE V 中，ADE AED ∠=∠，DF EF =，AD ，EF 的延长线相交于点B 、AE ，DF 的延长线相交于点C ．求证BD CE =．2．（23-24八年级上·江苏南京·阶段练习）如图，在ABC 中，AD 是三角形的中线，点F 在中线AD 上，且BF AC =，连接并延长BF 交AC 于点E ，求证：AFE CAF ∠=∠．题型04根据三线合一求解【例题】（23-24八年级下·贵州毕节·阶段练习）如图，在三角形框架ABC 中，AB AC =，AO 是连接点A 与BC 中点O 的支架．若80BAC ∠=︒，则BAO ∠的度数为．【变式训练】1．（23-24八年级下·全国·课后作业）如图，在ABC 中，AB AC =，AD 平分BAC ∠，点E 在边AB 上，且BD BE =．若100BAC ∠=︒，则ADE ∠的大小为．2．（23-24八年级上·吉林长春·阶段练习）如图，在等腰ABC 中，5AB AC ==，AD 是ABC 的高，6BC =，E F 、分别是AB AD 、上一动点，则BF EF +的最小值为．题型05根据三线合一证明【例题】（23-24八年级下·全国·课后作业）如图，在ABC 中，90BAC ∠=︒，E 为边BC 上的点，且AB AE =，D 为线段BE 的中点，过点E 作EF AE ⊥，过点A 作AF BC ∥，且AF 、EF 相交于F ．(1)求证：C BAD ∠=∠；(2)求证：AC EF =．【变式训练】1．（23-24八年级上·云南红河·阶段练习）如图，在ABC 中，AB AC =，AD 是BC 边上的中线，BE AC ⊥于点E ．(1)求证：AD BC ⊥；(2)求证：=CBE BAD ∠∠．2．（23-24八年级上·江苏扬州·期末）在ABC 中，90ACB ∠=︒，AC BC =．(1)如图1，BE CE ⊥于点E ，AD CE ⊥于点D ，求证：ACD CBE ≌；(2)如图2，BE CE ⊥于点E ，CE 交AB 于点F ，若AC AF =，2BE =，则CF 的长为_______．题型06根据等边三角形的性质求解【例题】（23-24八年级下·山东枣庄·阶段练习）如图，在等边ABC 中，D 、E 分别为边BC 、AC 上的点，AD 与BE 相交于点P ，若BD CE =，则APE ∠=．【变式训练】1．（23-24八年级下·江西吉安·阶段练习）如图，在ABC 中，90,30,6A B AC ∠=︒∠=︒=厘米，点D 从点A 开始以1厘米/秒的速度向点C 运动，点E 从点C 开始以2厘米秒的速度向点B 运动，两点同时运动，当运动时间为秒时，DEC 是等边三角形．2．（23-24九年级下·河南商丘·阶段练习）在等边三角形ABC 中，8AB =，点P 在BC 边上．若7AP =，则BP 的长为．题型07根据等边三角形的性质证明【例题】（23-24八年级下·广东佛山·阶段练习）如图，ABC 为等边三角形，点E 、F 分别在边AC BC 、上，AE CF =，10BE =，AF 与BE 相交于点D ，3AD =．(1)求证：ABF BCE ≌ ．(2)求DF 的长度．【变式训练】1．（2024八年级下·全国·专题练习）如图1，等边三角形BCD 和等边三角形ACE ，连接AD ，BE ，其中AC BC >．(1)求证：AD BE =；(2)如图2，当点A C 、、B 在一条直线上时，AD 交CE 于点F ，BE 交CD 于点G ，求证：BG DF =；(3)利用备用图补全图形，直线AD ，BE 交于点H ，连接CH ，若3DH =，5CH =，直接写出BH 的长．2．（2024八年级下·全国·专题练习）已知ABC 是等边三角形，D 为射线BC 上一动点，连接AD ，以AD 为边在直线AD 右侧作等边三角形ADE ．(1)如图1，当点D 在BC 边上时，连接CE ，此时AB ，CD ，CE 之间的数量关系为______，ACE ∠=______；(2)如图2，当点D 在BC 的延长线上时，连接CE ，（1）中AB ，CD ，CE 之间的数量关系是否仍然成立？若成立，请说明理由；若不成立，请写出新的结论及证明过程；(3)如图3，当点D 在射线BC 上运动时，取AC 的中点F ，连接EF ，当EF 的值最小时，请直接写出CFE ∠的度数．一、单选题1．（23-24八年级下·广东佛山·期中）等腰三角形的两边长分别为3和6，则这个三角形的周长是（）A ．15B ．12C ．12或15D ．92．（2024·甘肃天水·一模）若等腰三角形中有一个角等于50︒，则这个等腰三角形的顶角的度数为（）A ．50︒B ．80︒C ．65︒或50︒D ．50︒或80︒3．（2024年安徽省名校之约中考第一次联考数学试题）如图，AB CD ∥，点E 为直线AB 上方一点，连接BD ，DE ，BE ．若DE CD ⊥，BE DE =，25BDC ∠=︒，则ABE ∠的度数是（）A ．125︒B ．130︒C ．135︒D ．140︒4．（22-23八年级上·江苏无锡·期中）如图，在ABC 中，6BC =，ABC ∠与ACB ∠的平分线交于点O ，过点O 作BC 的平行线分别交AB 、AC 于点M 、N ，AMN 的周长是13，则ABC 的周长是（）A ．18B ．19C ．20D ．215．（23-24八年级上·江苏徐州·期中）如图，在Rt ABC △中，90ACB ∠=︒，10cm AB =，6cm AC =，动点P 从点B 出发，沿射线BC 以1cm/s 的速度运动，设运动的时间为t 秒，若ABP 是等腰三角形时，则t 的值为（）A ．10B ．16C ．10或16D ．10或16或254二、填空题6．（22-23八年级下·河南郑州·期中）已知等腰三角形的两边长为x y ，，且满足()2420x x y -+-=，则三角形的周长为．7．（23-24七年级下·吉林长春·阶段练习）一个等腰三角形的周长是17，已知它的一边长是5，则另外两边的长分别是．8．（23-24九年级下·福建福州·期中）如图，已知直线12l l ∥，点,A D 在直线1l 上，以点A 为圆心，适当长为半径画孤，分别交直线12,l l 于,C B 两点，连接,AB BC ．若115BCD ∠=︒，则1∠的度数为．9．（23-24八年级下·江苏泰州·期中）如图，ABC 和ADE V 都是顶角为45︒的等腰三角形，AB AD >，BC 、DB 分别是两个等腰三角形的底边，点B 、D 、E 三点恰好落在一条直线上，若18BAD EBC ∠=︒∠=，度．10．（23-24八年级下·陕西西安·阶段练习）如图，已知60AOB ∠=︒，点P 在边OA 上，5OP =，点M 、N 在边OB 上，PM PN =，若2MN =，则OM =．三、解答题11．（23-24七年级上·山东青岛·期末）（1）如图1，已知CE 与AB 交于点E ，AC BC =，12∠=∠，则AE 与BE 的数量关系是______；（2）如图2，已知CD 的延长线与AB 交于点E ，AD BC =，34∠∠=，探究AE 与BE 的数量关系，并说明理由．12．（23-24八年级上·安徽阜阳·期末）如图，在ABC 中，AB AC =，AD 平分BAC ∠．以点A 圆心，AD 长为半径画弧，与AB ，AC 分别交于点E ，F ，连接DE ，DF ．(1)求证：BDE CDF ≌；(2)若80BAC ∠=︒，求BDE ∠的度数．13．（22-23八年级上·湖北武汉·期末）如图，Rt ABC △中，90ACB ∠=︒，AC BC =，点D 在斜边AB 上，且AD AC =，过点B 作BE CD ⊥交直线CD 于点E ，过点A 作AF CD ⊥于点F ．(1)求BCD ∠的度数；(2)求证：DF BE =．14．（23-24八年级上·陕西安康·期末）如图，在ABC 中，AC BC =，点D 是AB 上一点，DE BC ⊥于点E ，EF AC ⊥于点F ．(1)若点D 是AB 的中点，求证：12BDE C ∠=∠；(2)若160ADE =∠︒，求DEF ∠的度数．15．（23-24八年级上·陕西商洛·期末）如图，ABC ，ADE V 均是等边三角形，点B ，D ，E 三点共线，连接CD ，CE ，CD BE ⊥．(1)求证：BD CE =；(2)若线段3DE =，求线段CE 的长．16．（22-23七年级下·四川成都·期末）已知，在等边ABC 中，点D 为射线BA 上一点（点D 与点B 不重合），连接CD ，以DC 为边在BC 上方作等边DCE △，连接AE ．(1)如图1，当点D 是AB 边中点时，求ADE ∠的度数；(2)求证：AE BD =；(3)如图2，当动点D 在BA 的延长线上时，以DC 为边在其下方作等边DCF ，连接BF ，求线段AB ，AE ，BF 之间的等量关系式．。

第五章生活中的轴对称3 简单的轴对称图形（第1课时）会宁县桃林中学王伟彦一、教学目的1. 探索并掌握等腰三角形的轴对称性及其相关性质。

3. 掌握等边三角形的轴对称性及其有关性质。

二、教学过程⑴（整体浏览课本，确定学习目标）1、（课本121页引例）认识等腰三角形是轴对称图形。

掌握等腰三角形对称轴的“三线合一”及相关性质。

2、（课本121页想一想）认识等边三角形是轴对称图形。

掌握等边三角形的相关特征。

⑵创设情境导入新课1. 认识等腰三角形，介绍等腰三角形的概念及各部分名称。

⑶动手操作探求新知等腰三角形是一种特殊的三角形，它除具有一般三角形的性质外，还有一些特殊的性质吗？拿出你的等腰三角形纸片，把纸片折折看，你能发现什么现象吗？1. 思考（1）等腰三角形是轴对称图形吗？找出对称轴。

（2）顶角的平分线所在的直线是等腰三角形的对称轴吗？（3）底边上的中线所在的直线是等腰三角形的对称轴吗？底边上的高呢？（4）沿对称轴折叠，你能发现等腰三角形的哪些特征？2.归纳(1)等腰三角形是轴对称图形。

(2)∠B =∠C(3 )∠BAD＝∠CAD，AD为顶角的平分线(4)∠ADB=∠ADC=90°AD为底边上的高(5 )BD=CD，AD为底边上的中线。

等腰三角形的特征：1）.等腰三角形是轴对称图形2）.等腰三角形的顶角平分线、底边上的中线、底边上的高重合（也称“三线合一”），它们所在的直线都是等腰三角形的对称轴。

3）.等腰三角形的两个底角相等。

3.推理等腰三角形顶角的平分线、底边上的中线、底边上的高重合（也称为“三线合一”）.证明：因为AD是角平分线,所以∠BAD= ∠ CAD在ΔABD和ΔA CD中,因为AB=AC, ∠BAD= ∠CAD,AD=AD所以ΔABD ≌ΔACD所以BD=CD, ∠ADB=∠ADC=90˚所以AD是ΔABC的角平分线、底边上的中线、底边上的高。

⑷知识推广1．等边三角形的有关概念有几条对称轴？2. 你能发现等边三角形的哪些特征？⑸知识应用2.利用圆规⑹随堂练习1、①若等腰三角形的一个内角为40°,则它的另外两个内角为________。

第五章生活中的轴对称5.3简单的轴对称图形第1课时教学设计一、教学目标1.掌握等腰三角形的定义，利用定义解决问题；2.掌握等腰三角形和等边三角形的轴对称性、相关性质及判定．二、教学重点及难点重点：等腰三角形的相关概念；掌握等腰三角形的轴对称性、有关性质及判定．难点：应用等腰三角形的概念和性质解决等腰三角形解决问题．三、教学准备多媒体课件四、相关资源相关图片，微课，动画五、教学过程【问题情境】在前面的学习中，我们认识了轴对称图形，探究了轴对称的性质，•并且能够作出一个简单平面图形关于某一直线的轴对称图形，还能够通过轴对称变换来设计一些美丽的图案．这节课我们就从轴对称的角度来认识一些我们熟悉的几何图形．问题1：三角形是轴对称图形吗？有的三角形是轴对称图形，有的三角形不是．问题2：什么样的三角形是轴对称图形？满足轴对称的条件的三角形就是轴对称图形，也就是将三角形沿某一条直线对折后两部分能够完全重合的就是轴对称图形．我们这节课就来认识一种是轴对称图形的三角形——等腰三角形．设计意图：通过回顾轴对称图形及轴对称性质，引出本节课所要探究的内容，让学生明确探究方向．【探究新知】探究一：认识等腰三角形 观察图片：这些三角形有什么共同特点？定义：有两条边相等的三角形叫等腰三角形探究二：等腰三角形的性质活动1.作等腰三角形（1）如图所示，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC 有什么特点？（2）鼓励学生用不同的方法得到等腰三角形，例如还可以像下面这样来作一个等腰三角形．（顶角底角底角腰腰底边)作一条直线l ，在l 上取一点A ，在l 外取一点B ，作出点B 关于直线l 的对称点C ，连接AB ，BC ，CA ，则可得到一个等腰三角形．设计意图：以动手操作的形式得出一个等腰三角形，鼓励学生充分的进行交流，充分利用等腰三角形的特征，逆向思维，达到学以致用的目的.同时充分体现了数学来源于生活，同时也更好的服务于生活的理念.活动2.思考：（1）等腰三角形是轴对称图形吗？请找出它的对称轴． （2）等腰三角形顶角平分线所在的直线是它的对称轴吗？（3）等腰三角形底边上的中线所在的直线是它的对称轴吗？底边上的高所在的直线呢？ （4）沿对称轴对折，你能发现等腰三角形的那些特征？说说你的理由.因为等腰三角形的两腰相等，所以把这两条腰重合对折便知：等腰三角形是轴对称图形，它的对称轴是折痕所在的直线．学生通过折叠，发现折痕两旁的部分互相重合，由此可知这个等腰三角形的两个底角相等，而且还可以知道顶角的平分线既是底边上的中线，也是底边上的高．由此可以得到:等腰三角形是轴对称图形.性质1：等腰三角形的两个底角相等（简写成“等边对等角”）；性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（简写成“三线合一”）．由上面折叠的过程获得启发，我们可以通过作出等腰三角形的对称轴，得到两个全等的三角形，从而利用三角形的全等来证明这些性质．活动3.等腰三角形的性质1的证明：证法1：如图，在△ABC 中，AB ＝AC ，作底边BC 的中线AD ，则BD ＝CD ． 在△ABD 和△ACD 中，AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩，，， ∴△ABD ≌△ACD （SSS ）．∴∠B ＝∠C ．证法2：如图，在△ABC 中，AB ＝AC ，作顶角∠BAC 的角平分线AD ， ∴∠1＝∠2．在△ABD 和△ACD 中，1=2AB AC AD AD =⎧⎪∠∠⎨⎪=⎩，，， ∴△ABD ≌△ACD （SAS ）． ∴∠B ＝∠C ．几何语言表示：在△ABC 中，∵AB ＝AC ， ∴∠B ＝∠C ．活动4.等腰三角形性质2的证明：性质2可以分解为三个命题，下面我们来证明“等腰三角形的底边上的中线也是底边上的高和顶角平分线”．已知：如图，△ABC 中，AB ＝AC ，AD 是底边BC 的中线．求证：∠BAD ＝∠CAD ，AD ⊥BC ．证明：∵AD 是底边BC 的中线， ∴BD ＝CD ．在△ABD 和△ACD 中，AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩，，， ∴△ABD ≌△ACD （SSS ）． ∴∠BAD ＝∠CAD ， ∠ADB ＝∠ADC ．∵∠ADB ＋∠ADC ＝180°， ∴∠ADB ＝90°． ∴AD ⊥BC ．教师鼓励学生仿照示例口述另两个命题的证明过程． 几何语言表示：在△ABC 中，（1）∵AB ＝AC ，BD ＝CD ， ∴AD ⊥BC ，∠BAD ＝∠CAD ． （2）∵AB ＝AC ，∠BAD ＝∠CAD ， ∴AD ⊥BC ，BD ＝CD ． （3）∵AB ＝AC ，AD ⊥BC ， ∴∠BAD ＝∠CAD ，BD ＝CD ．在等腰三角形性质的探索过程和证明过程中，“折痕”“辅助线”发挥了非常重要的作用，由此得到：等腰三角形是轴对称图形，底边上的中线（或顶角平分线、底边上的高）所在直线就是它的对称轴．设计意图：通过引导学生动手操作，探索和发现等腰三角形的性质，加深学生对等腰三角形性质的直观感知，并尝试构造全等三角形给出推理证明，锻炼学生探索和发现问题并解决问题的能力．探究三：等边三角形1. 定义：三边都相等的三角形是等边三角形也叫正三角形.2.性质：（1）等边三角形是轴对称图形吗？找出对称轴（2）你能发现它的哪些特征？结论：（1）等边三角形是轴对称图形；（2）等边三角形每个角的平分线和这个角的对边上的中线、高线重合（“三线合一”），它们所在的直线都是等边三角形的对称轴。

简单的轴对称图形（二）（一）教学设计●教学目标【知识与技能目标】1．进一步理解轴对称、轴对称图形的概念。

2．探索等腰三角形的性质，掌握等腰三角形的轴对称性及其相关性质。

3．会利用轴对称的有关性质解决实际问题。

【过程与方法目标】1．学生通过实验探索发现等腰三角形的性质，并能利用等腰三角形的性质解决实际问题。

2．学生亲自经历“问题情境——建立模型——求解——解释应用”的基本过程，体验数学知识在实际生活中的广泛应用。

3．通过轴对称图形的探究，培养形式分析、概括的能力【情感与态度目标】1．通过优美的等腰三角形“三线合一”的性质，体会几何图形的和谐美。

2．在学习活动中，学会与同伴交流，体会获得成功的喜悦。

3．通过对实际问题的解决，使学生感受数学与我们的生活息息相关。

●教学重点：探索等腰三角形的轴对称性●教学难点：掌握等腰三角形有关概念及特性；加深等腰三角形“三线合一”的理解和应用●教具准备：等腰三角形纸片、三角板、量角器、多媒体（若没有可直接用图片代替）多媒体动画展示折叠过程． （三）例题精选 例1 已知，如图，BC ＞AB ，BD 平分∠ABC ，且AD=DC ，求证：∠A+∠C=180°．例2 已知，如图（1），等边△ABC 和点P ，设点P 到△ABC 三边AB 、AC 、BC 的距离分别为h 1，h 2，h 3，△ABC 的高为h ，“若点P 在一边BC 上，此时h 3=0，可得结论：h 1+h 2+h 3=h ”请直接应用上述信息解决下列问题：当点P 在△ABC 内（如图2）、点P 在△ABC 外（如图3）这两种情况时，上述结论是否成立？若成立，请说明理由；若不成立，h 1，h 2，h 3与h 之间又有怎样的关系？请写出你的猜想，不需证明 ．NKM M PP FE E DDCCB B AAM (2)F Q P(3)(1)EDCBA例3 如图，是某城市部分街道示意图，△ABC 、CDC BA A△CDE都为正三角形，A、B、C、D、E、F、G、H为公共汽车停靠站，公车甲从A站出发，按照A、H、G、D、E、C、F的顺序到达F站，公车乙从B站出发，沿F、H、E、D、C、G的顺序到达G站，如果甲、乙分别从A、B站出发，在各站耽误的时间相同，两车速度也一样，试问哪已辆公车先到达指定车站？为什么？．（四）练习精选1．等腰三角形的一腰为6，底边长为4，则这个等腰三角形的周长为（）A．13；B．14；C．15；D．16．2．已知，等腰三角形的一边长为3，一边长等于6，则它的周长等于（）A．12 B．15 C．12或15 D．15或18 3．在△ABC中，AB=AC，AB的中垂线与AC所在直线相交所得的锐角为50°，则底角B的大小为4．等腰三角形的一个角是110°，它的另外两个角是；等腰三角形的一个角是80°，它的另外两个角为5．如图，△ABC中，AB=AC，BD⊥AC于D，求证：∠DBC=21∠A6．如图，点D在AC上，点E在AB上，且AB=AC，BC=BD，AD=DE=BE，求∠A的度数．（五）知识拓展与提高练习7．如图所示，BD为∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD于M，PN⊥CD于N，则PM=PN，你认为这个结论对吗？请阐述你的理由。