西格玛水平与不良率对照表

格式：pdf
大小：163.87 KB
文档页数：1

下载文档原格式

不良率与西格玛(σ)水平的关系

不良率与西格玛（σ）水平的关系制程能力指标Cp或Cpk之值在产品或制程特性分布为正态且在管制状态下时，通过正态分布的概率计算，可以换算为该产品或制程特性的良率或不良率，同时也可以几个Sigma来对照。

现以产品或制程特性中心没偏移目标值、中心偏移目标值1.5σ及中心偏移目标值T/8分别说明，因为有质量专家认为，对于Sigma水平较小时，偏移的幅度应相对的小，才较合理，因此提出偏移目标值T/8的考虑，在分析前，先定义以下几个符号：●X：个别产品或制程特性值●USL：规格上限●LSL：规格下限●m：目标值或规格中心，一般为(USL＋LSL)/2●T=USL-LSL：规格界限宽度●μ：产品或制程特性中心或平均数●σ：产品或制程特性标准差1、产品或制程特性中心没偏移目标值(即Ca=0)，即μ＝m＝（USL＋LSL）/2Sigma 水平=±kσ；即 T ＝ USL - LSL ＝ 2 kσCp＝规格界限宽度/ 6σ＝T / 6σ＝（USL - LSL）/ 6σ＝2 kσ/ 6σ＝k / 3＝Cpk不良率＝ P [ | X | > kσ] ＝ P [ | Z |> k ]＝标准常态分布右尾概率×2良率＝（ 1-不良率）Sigma水平(±kσ)Cpk/ Cp良率%PPM不良率2σ0.6795.45%45,6003σ 1.0099.73%2,7004σ 1.3399.9937%635σ 1.6799.999943%0.576σ 2.0099.9999998%0.0022、产品或制程特性中心偏移目标值1.5σ，即μ＝（USL＋LSL）/2 ± 1.5σSigma 水平=±kσ；即 T＝USL-LSL＝ 2 kσ●产品或制程特性中心大于目标值1.5σC PU＝（USL - μ）/3σ＝（kσ- 1.5σ）/ 3σ=（ k-1.5 ） / 3C PL＝（μ- LSL） / 3σ= （ kσ+ 1.5σ） / 3σ= （k+1.5） /3Cpk = MIN{CPU，CPL}＝（k-1.5）/3不良率＝P [ X > USL ] + P [ X < LSL ] = P [ Z > 3 x CPU ] +P[ Z > 3 x CPL ]＝P [ Z > （ k -1.5 ） ] + P [ Z > （ k + 1.5 ）]良率＝（ 1- 不良率）●产品或制程特性中心小于目标值1.5σCPU＝（USL－μ） / 3σ＝（kσ+ 1.5 σ）/ 3σ＝（k+1.5） /3CPL＝（μ－LSL） / 3σ＝（kσ+ 1.5 σ）/ 3σ＝（k-1.5） /3Cpk＝ MIN{CPU，CPL}＝（k-1.5） /3不良率＝ P [ X > USL ] + P [ X < LSL ]＝P[ Z > 3 x CPU ] + P[ Z > 3 x CPL ]＝ P[ Z > （ k + 1.5 ）] + P[Z > 3 x （ k - 1.5 ） ]良率＝（ 1-不良率）Sigma水平Cpk Cp良率%PPM不良率2σ0.670.1769.13%308,770 3σ 1.000.5093.32%66,811 4σ 1.330.8399.379%6,2105σ 1.67 1.1799.99767%2336σ 2.00 1.5099.99966% 3.4 3、产品或制程特性中心偏移目标值T/8，即μ＝（USL＋LSL）/2 + - T / 8Sigma 水平= + - kσ；即T＝USL-LSL＝ 2kσ●产品或制程特性中心大于目标值T/8＝2kσ/ 8＝（k / 4）σCPU＝（USL－μ）/ 3σ＝（kσ-（ k / 4）σ）/ 3σ＝3k/12CPL＝（μ－LSL）/3σ＝（kσ+（ k / 4）σ）/ 3σ＝5k/12Cpk＝ MIN{CPU，CPL}＝3k/12不良率＝P [ X > USL ] + P [ X < LSL]＝P[ Z > 3 x CPU ] + P[ Z > 3x CPL ]＝P[ Z > 3k / 12 ）] + P[ Z > P [ Z > 5k /12 ]良率＝（ 1- 不良率）●产品或制程特性中心小于目标值T/8＝2kσ/ 8＝（ k / 4）σCPU＝（USL－μ）/ 3σ＝（kσ+ （k / 4）σ） / 3σ＝ 5k/12CPL＝（μ－LSL）/ 3σ＝（kσ- （k / 4）σ） / 3σ＝ 3k/12。

±1西格玛对应的合格率

±1西格玛对应的合格率±1西格玛对应的合格品率为68.27%，不合格品率为317300PPM。

请注意，西格玛水平是描述过程能力或产品质量水平的一个统计量，它表示过程的标准偏差与公差带的宽度之比。

因此，不同行业或不同产品可能对应不同的西格玛水平。

这里给出的±1西格玛对应的合格率是一个一般情况下的参考值，具体还需要根据实际情况进行评估。

西格玛水平在不同行业中的标准可能会有所不同，因为不同行业对于产品质量和过程能力的需求和要求可能存在差异。

然而，一般来说，西格玛水平可以分为以下几个等级：1.一西格玛（1σ）：这是最低的水平，通常表示过程能力很差，产品缺陷率很高。

在一西格玛水平下，大约690,000个机会中会有一个缺陷。

2.二西格玛（2σ）：这表示过程能力略好一些，但仍然有很大的改进空间。

在二西格玛水平下，每百万个机会中将有308,000个缺陷。

3.三西格玛（3σ）：这是很多企业的基本要求，表示过程能力达到了中等水平。

在三西格玛水平下，每百万个机会中将有66,800个缺陷。

4.四西格玛（4σ）：这表示过程能力较好，可以有效地控制产品和服务的缺陷率。

在四西格玛水平下，每百万个机会中将有6,210个缺陷。

5.五西格玛（5σ）：这是优秀的水平，表示过程能力非常高，只有极少的缺陷。

在五西格玛水平下，每百万个机会中将有230个缺陷。

6.六西格玛（6σ）：这是卓越的水平，表示过程能力达到了极高的水平，几乎没有缺陷。

在六西格玛水平下，每百万个机会中将只有3.4个缺陷。

需要注意的是，这些西格玛水平只是参考值，具体的标准还需要根据不同的行业、不同的产品和不同的需求进行确定。

同时，这些水平也不是绝对的，企业可以根据自己的实际情况和目标来制定适合自己的西格玛水平标准。

CPK、Sigma和PPM的换算关系

过程能力指数（Cp和Cpk）表示的是过程在稳定（即没有特殊原因干扰产出品的特性或者说是在可控（under control）的）状态下能使其产出品达到可接受标准的程度的指标。

按照常识，Cpk越高越好，产品的不良率也越低。

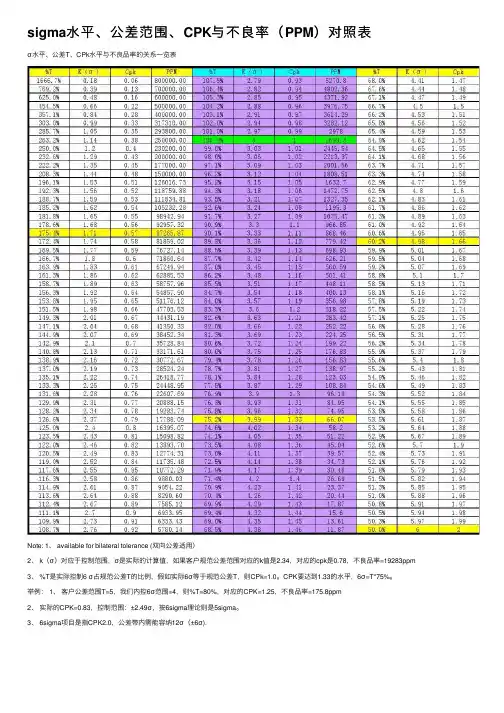
SQE在PPAP审核时，要求供应商提交的过程能力报告，关键特性的Cpk大于1.33，此时供应商内部的百万分之不良率PPM为63。

拓展到Cpk=1.0，Cpk=1.67的PPM如下：在不考虑偏移的情况下：Cpk=1.33 对应4σ 水平其PPM=63.3；Cpk=1.67 对应5σ 水平其PPM=0.570；Cpk=2.0 对应6σ 水平其PPM=0.0020；那么，这个值是怎么来的，其他Cpk对应的PPM数值是多少？过程能力指数Cp或Cpk在产品或制程特性分布为正态且在稳定状态下时，通过正态分布的概率计算，可以换算为该产品或制程特性的良率或不良率，同时也可以几个Sigma来对照。

CPK是过程能力，西格玛水平是管理水平，PPM是管理结果。

下文将以产品或制程特性中心没偏移目标值和中心偏移目标值1.5σ说明。

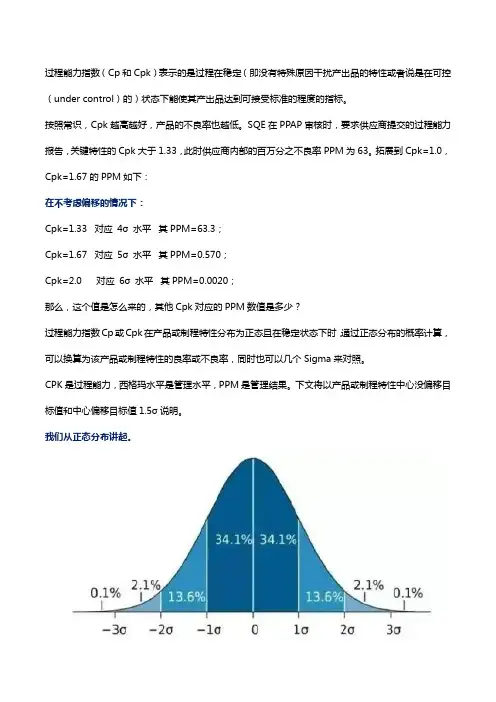
我们从正态分布讲起。

若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。

其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。

当μ = 0，σ = 1时的正态分布是标准正态分布。

若随机变量X，服从一个位置参数为μ、尺度参数为σ的概率分布，其概率密度函数为：当μ=0，σ=1时，正态分布就成为标准正态分布。

我们对其积分，也就是求面积，所得值为1。

（每个质量人追求的100.00%合格）接下来，我们谈一下什么是西格玛水平。

西格玛水平Sigma Level：过程能力的一种衡量指标，将过程分布的平均值、标准偏差与质量特性的目标值、规格线结合起来。

西格玛水平越高，过程满足质量要求的能力就越强，反之，西格玛水平越低，过程满足质量要求的能力就越低。

我们可以简单的理解为规格线与目标值间的距离最少能容纳k个标准偏差σ，当k = 3时，我们称之为3西格玛水平，上下规格极限之差为6σ。

6西格玛6个标准差

控制
确保所做旳改善能够连续下去。衡量不能中断，才干防止错误再度发生。在过去许多流
程改善方案里，往往忽视了控制旳观念；而在六个原则差中，控制是它能长久改善品质与
成本旳关键。
假如成功推动，6西格玛所带来旳，将是变化企业惯性，让员工能够不断问问题，并谋求更加好旳处理方案，让企业常处于向上爬升旳斜率上。
16
2
6西格玛旳主要原则 (一)
在推动6西格玛时，企业要真正能够取得巨大成效，必须把6西格玛当成一种管理哲学。这个哲学里，有六个主要主旨，每项主旨背后都有诸多工具和措施来支持.
3
6西格玛旳主要原则(二)
真诚关心顾客。
6西格玛把顾客放在第一位。例如在衡量部门或员工绩效时，必须站在顾客旳角度思索。先了解顾客旳需求是什么，再针对这些需求来设定企业目旳，衡量绩效。
6西格玛
1西格玛＝690000次失误／百万次操作 2西格玛＝308000次失误／百万次操作 3西格玛＝66800次失误／百万次操作 4西格玛＝6210次失误／百万次操作 5西格玛＝230次失误／百万次操作 6西格玛＝3.4次失误／百万次操作 7西格玛＝0次失误／百万次操作
1
什么是6西格玛
"σ"是希腊文旳字母，是用来衡量一种总数里原则误差旳统计单位。一般企业旳瑕疵率大约是3到4个西格玛，以4西格玛而言，相当于每一百万个机会里，有6210次误差。假如企业不断追求品质改善，到达6西格玛旳程度，绩效就几近于完美地达成顾客要求，在一百万个机会里，只找得出3.4个瑕疪。
13
为何要用6西格玛管理(一)
为了生存： "为何要开展6西格玛管理？"摩托罗拉旳回答是：为了生存。从70年代到80年代，摩托罗拉在同日本旳竞争中失掉了收音机和电视机旳市场，后来又失掉了BP机和半导体旳市场。1985年，企业面临倒闭。一种日本企业在70年代并购了摩托罗拉旳电视机生产企业。经过日本人旳改造后，不久投入了生产，而且不良率只有摩托罗拉管理时旳1/20。他们使用了一样旳人员、技术和设计。显然问题出在摩托罗拉旳管理上。在市场竞争中，严酷旳生存现实使摩托罗拉旳高层接受了这么旳结论："我们旳质量很臭"。在其CEO旳领导下，摩托罗拉开始了6西格玛质量之路。今日，"摩托罗拉"成为世界著名品牌，1998年，摩托罗拉企业取得了美国鲍德理奇国家质量管理奖。他们成功旳秘密就是6西格玛质量之路。是6西格玛管理使摩托罗拉从濒于倒闭发展到当今世界出名旳质量与利润领先企业。

SIGMA水平计算表

பைடு நூலகம்
(2) 只有规格下限的情况
(3) 上、下限规格齐全的情况平均规格上限超上限推测不良率全体推测不良率 DPMO 2.3 5 0.012224473 0.413518147 413,518.1 标准偏差规格下限超下限推测不良率 1.2 2 0.401293674 2. 数据没有散布的情况 1) 望小特性现水平先进水平目标水平 2) 望大特性现水平先进水平目标水平 16 22 19 → → → 4.36 σ 6.00 σ 5.18 σ 18 12 14 → → → 4.00 σ 6.00 σ 5.14 σ
3) Continuous(连续型) Type (1) 只有规格上限的情况平均 2.3 平均 2.3 标准偏差 1.2 标准偏差 1.2 规格上限 5 规格下限 1 不良率 0.012224473 不良率 0.139330247 DPMO 12,224.5 DPMO 139,330.2 Z-Value 2.25 Z-Value 1.08 Z-Value 0.22 σ -Level 3.75 σ -Level 2.58 σ -Level 1.72
1.标准方法 1) Defective(不良) Type 检验数 1,200 不良数 14 不良率 0.011666667 DPMO 11,666.7 Z-Value 2.27 σ -Level 3.77
2) Defect(缺点) Type 单位数 351 缺点数 10 DPU 0.028490028 不良率 0.028088014 DPMO 28,088.0 Z-Value 1.91 σ -Level 3.41

sigma水平、公差范围、CPK与不良率（PPM）对照表

2k对应于控制范围是实际的计算值如果客户规范公差范围对应的k值是234对应的cpk是078不良品率19283ppm
sigma水平、公差范围、 CPK与不良ห้องสมุดไป่ตู้（ PPM）对照表
σ水平、公差T、CPk水平与不良品率的关系一览表
Note: 1、 available for bilateral tolerance (双向公差适用） 2、 k（σ）对应于控制范围，σ是实际的计算值，如果客户规范公差范围对应的k值是2.34，对应的cpk是0.78，不良品率=19283ppm 3、 %T是实际控制6 σ占规范公差T的比例，假如实际6σ等于规范公差T，则CPk=1.0。CPK要达到1.33的水平，6σ=T*75%。举例： 1、客户公差范围T=5，我们内控6σ范围=4，则%T=80%，对应的CPK=1.25，不良品率=175.8ppm 2、实际的CPK=0.83，控制范围：±2.49σ，按6sigma理论则是5sigma。 3、 6sigma项目是指CPK2.0，公差带内需能容纳12σ（±6σ).

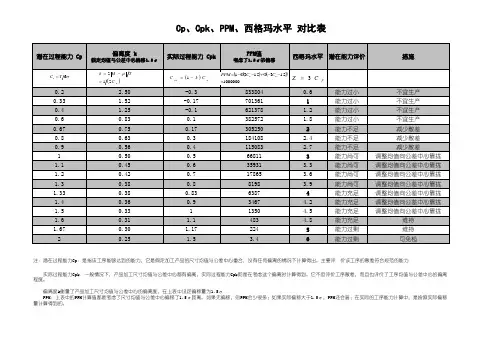
Cp-Cpk-PPM-西格玛水平

Cp、Cpk、PPM、西格玛水平对比表
注：潜在过程能力Cp：是指该工序能够达到的能力，它是假定加工产品的尺寸均值与公差中心重合，没有任何偏离的情况下计算得出。

主要评价该工序的散差符合规范的能力
实际过程能力Cpk：一般情况下，产品加工尺寸均值与公差中心都有偏离，实际过程能力Cpk即是在考虑这个偏离时计算得到。

它不但评价工序散差，而且也评价了工序均值与公差中心的偏离程度。

偏离度k衡量了产品加工尺寸均值与公差中心的偏离度，在上表中设定偏移量为1.5σ
PPM：上表中的PPM计算值都是考虑了尺寸均值与公差中心偏移了1.5σ距离。

如果无偏移，则PPM会少很多；如果实际偏移大于1.5σ，PPM还会高；在实际的工序能力计算中，是按照实际偏移量计算得到的。

【转帖】Sigma水平和缺陷率的对应关系：正态分布中心和1.5标准差偏移

【转帖】Sigma⽔平和缺陷率的对应关系：正态分布中⼼和1.5
标准差偏移
Sigma⽔平和缺陷率的对应关系：正态分布中⼼和有1.5个标准差偏移
在过程稳定时，若给出了规范限，过程的平均与标准差后，我们可以通过查正态分布表，获得不合格品率。

这⾥给出⼀张在不同的δσ质量⽔平下对照表--每⼀百万个产品中的不合格品数。

品质协会()备注：设规范限为（LSL，USL），规范限的宽度为T，规范的中⼼为M，过程的均值为µ，标准差为δ，⼀般情况下⽤的是|M-µ|=1.5δ，表⽰有偏移，如果M=µ，表⽰为⽆偏移。

不合格品率(ppm)
T/2包含的σ个数δM=µ|M-µ|=1.5
1317400697700
245400308733
3270066803
4636210
50.57233
60.002 3.4
上⾯是不合格率，合格率是1，000,000-上⾯的数字，然后除以1，000,000就能够算出来，下⾯为您简要介绍。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。