第三章 多元线性回归模型(Stata)

使用Stata进行数据分析的教程第一章：介绍StataStata是一种统计软件，经常被研究人员和学者用于数据分析和统计建模。

它提供了强大的数据处理和分析功能，可以应用于不同领域的研究项目。

本章介绍了Stata的基本功能和特点，包括数据管理、数据操作和Stata的界面等。

1.1 Stata的起源和发展Stata最初是由James Hardin和William Gould创建的，旨在为统计学家和社会科学研究人员提供一个数据分析工具。

随着时间的推移，Stata得到了广泛的应用，并逐渐发展成为一种强大的统计软件。

1.2 Stata的功能和特点Stata提供了许多数据处理和分析函数，包括描述性统计、回归分析、因子分析和生存分析等。

它还具有数据的管理功能，可以导入、导出和编辑数据文件。

Stata的界面友好，并且支持批处理和交互模式。

第二章：数据管理与准备在进行数据分析之前，首先需要准备和管理数据集。

本章将详细介绍Stata中的数据导入、数据清洗和数据变换等操作。

2.1 数据导入与导出Stata可以导入各种格式的数据文件，包括CSV、Excel和SPSS 等。

同时，Stata也支持将分析结果导出为不同的格式，如PDF和HTML等。

2.2 数据清洗和缺失值处理在实际研究中，数据常常存在缺失值和异常值。

Stata提供了处理缺失值和异常值的方法，可以通过删除、替换或插补来处理这些问题。

2.3 数据变换和指标构造数据变换是指将原始数据转化为适合分析的形式，常见的变换包括对数变换、差分和标准化等。

指标构造是指根据已有变量构造新的变量，如计算平均值和构造虚拟变量等。

第三章：描述性统计和数据可视化描述性统计是对数据集的基本统计特征进行总结和分析，而数据可视化则是通过图表和图形展示数据的特征和关系。

本章将介绍在Stata中进行描述性统计和数据可视化的方法。

3.1 中心趋势和离散程度的度量通过计算平均值、中位数和众数等指标来描述数据的中心趋势。

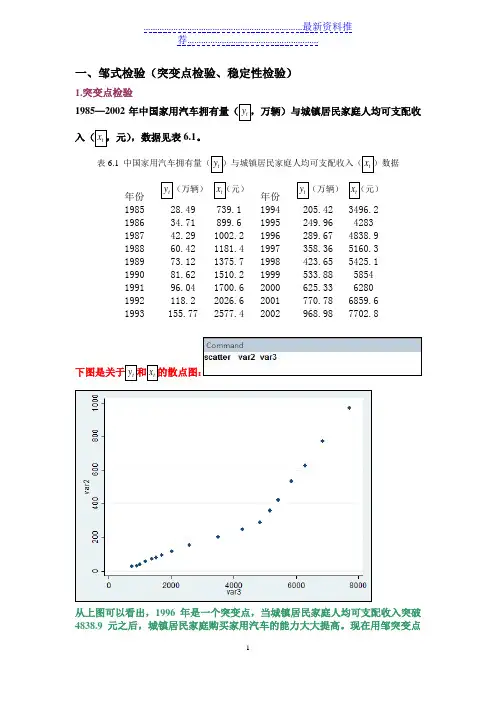
一、邹式检验（突变点检验、稳定性检验）1.突变点检验1985—2002年中国家用汽车拥有量（t y ，万辆）与城镇居民家庭人均可支配收入（t x ，元），数据见表6.1。

表6.1 中国家用汽车拥有量（t y ）与城镇居民家庭人均可支配收入（t x ）数据年份 t y （万辆） t x （元）年份 t y （万辆） t x （元）1985 28.49 739.1 1994 205.42 3496.2 1986 34.71 899.6 1995 249.96 4283 1987 42.29 1002.2 1996 289.67 4838.9 1988 60.42 1181.4 1997 358.36 5160.3 1989 73.12 1375.7 1998 423.65 5425.1 1990 81.62 1510.2 1999 533.88 5854 1991 96.04 1700.6 2000 625.33 6280 1992 118.2 2026.6 2001 770.78 6859.6 1993155.77 2577.42002968.98 7702.8下图是关于t y 和t x 的散点图：从上图可以看出，1996年是一个突变点，当城镇居民家庭人均可支配收入突破4838.9元之后，城镇居民家庭购买家用汽车的能力大大提高。

现在用邹突变点检验法检验1996年是不是一个突变点。

H0：两个字样本（1985—1995年，1996—2002年）相对应的模型回归参数相等H1：备择假设是两个子样本对应的回归参数不等。

在1985—2002年样本范围内做回归。

在回归结果中作如下步骤(邹氏检验)：1、Chow 模型稳定性检验（lrtest）用似然比作chow检验，chow检验的零假设：无结构变化，小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用似然比检验检验结构没有发生变化的约束得到结果如下;(如何解释？)2.稳定性检验（邹氏稳定性检验）以表6.1为例，在用1985—1999年数据建立的模型基础上，检验当把2000—2002 * 用F-test作chow间断点检验检验模型稳定性* chow检验的零假设：无结构变化，小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用F 检验检验结构没有发生变化的约束*计算和显示 F 检验统计量公式，零假设：无结构变化然后dis f_test 则得到结果;* F 统计量的临界概率然后 得到结果* F 统计量的临界值然后 得到结果(如何解释？)二、似然比（LR ）检验有中国国债发行总量（t DEBT ，亿元）模型如下：0123t t t t t DEBT GDP DEF REPAY u ββββ=++++其中t GDP 表示国内生产总值（百亿元），t DEF 表示年财政赤字额（亿元），t REPAY 表示年还本付息额（亿元）。

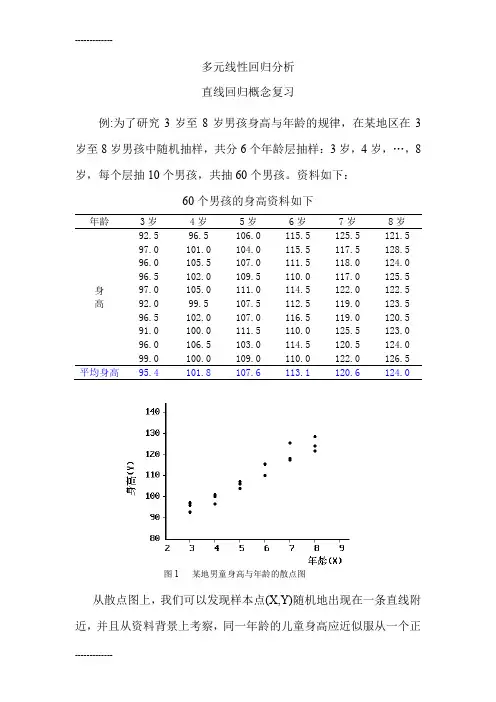
多元线性回归分析 直线回归概念复习例:为了研究3岁至8岁男孩身高与年龄的规律，在某地区在3岁至8岁男孩中随机抽样，共分6个年龄层抽样：3岁，4岁，…，8岁，每个层抽10个男孩，共抽60个男孩。

资料如下：60个男孩的身高资料如下年龄3岁 4岁 5岁 6岁 7岁 8岁 身 高92.5 96.5 106.0 115.5 125.5 121.5 97.0 101.0 104.0 115.5 117.5 128.5 96.0 105.5 107.0 111.5 118.0 124.0 96.5 102.0 109.5 110.0 117.0 125.5 97.0 105.0 111.0 114.5 122.0 122.5 92.0 99.5 107.5 112.5 119.0 123.5 96.5 102.0 107.0 116.5 119.0 120.5 91.0 100.0 111.5 110.0 125.5 123.0 96.0 106.5 103.0 114.5 120.5 124.0 99.0 100.0 109.0 110.0 122.0 126.5 平均身高95.4101.8107.6113.1120.6124.0从散点图上，我们可以发现样本点(X,Y)随机地出现在一条直线附近，并且从资料背景上考察，同一年龄的儿童身高应近似服从一个正图1 某地男童身高与年龄的散点图态分布，而儿童身高的总体均数应随着年龄增长而增大，并由每个年龄的身高样本均数与儿童年龄的散点图可以发现：这些点非常接近一条直线以及样本均数存在抽样误差，因此推测儿童身高的总体均数与年龄可能呈直线关系。

故假定身高Y 在年龄X 点上的总体均数X Y |μ与X 呈直线关系。

x μαβ=+y其中y 表示身高，x 表示年龄。

由于身高的总体均数与年龄有关，所以更准确地标记应为x μαβ=+y|x表示在固定年龄情况下的身高总体均数。

身高的样本均数与年龄的散点图故有理由认为身高的总体均数与年龄的关系可能是一条直线关系 上述公式称为直线回归方程。

stata多元logistic回归结果解读【实用版】目录一、多元 logistic 回归的概念与原理二、多元 logistic 回归模型的建立三、多元 logistic 回归结果的解读四、实际案例应用与分析五、总结正文一、多元 logistic 回归的概念与原理多元 logistic 回归是一种用于分析多分类变量与二元变量之间关系的统计分析方法。

它可以对多个自变量与因变量之间的关系进行同时分析，适用于研究多个因素对某一现象的影响。

logistic 回归是一种分类回归方法，它将二元变量（如成功/失败、是/否等）与多个自变量之间的关系建模为逻辑斯蒂函数，从而预测因变量的概率。

二、多元 logistic 回归模型的建立在建立多元 logistic 回归模型时，首先需要将数据整理成合适的格式。

模型中，因变量为二元变量（通常用 0 和 1 表示），自变量为多元变量（可以是分类变量或连续变量）。

然后，通过添加截距项，构建多元logistic 回归模型。

在 Stata 软件中，可以使用命令“logit”来实现多元 logistic 回归分析。

三、多元 logistic 回归结果的解读多元 logistic 回归的结果主要包括系数、标准误、z 值、p 值、OR 值等。

其中，系数表示自变量对因变量的影响程度，正系数表示正相关，负系数表示负相关；标准误表示系数的估计误差；z 值表示系数除以标准误的值，用于检验系数的显著性；p 值表示假设检验的结果，一般小于0.05 认为显著；OR 值表示风险比，表示一个自变量对因变量的影响程度。

四、实际案例应用与分析假设我们研究一个城市居民的出行选择行为，希望了解影响居民选择不同交通方式的因素。

我们可以建立一个多元 logistic 回归模型，将居民的出行方式作为因变量（二元变量），交通方式的类型、出行距离、出行时间等因素作为自变量。

通过分析模型结果，我们可以得到各个因素对居民出行选择行为的影响程度，从而制定更有针对性的交通政策。

多元线性回归模型引言：多元线性回归模型是一种常用的统计分析方法，用于确定多个自变量与一个连续型因变量之间的线性关系。

它是简单线性回归模型的扩展，可以更准确地预测因变量的值，并分析各个自变量对因变量的影响程度。

本文旨在介绍多元线性回归模型的原理、假设条件和应用。

一、多元线性回归模型的原理多元线性回归模型基于以下假设：1）自变量与因变量之间的关系是线性的；2）自变量之间相互独立；3）残差项服从正态分布。

多元线性回归模型的数学表达式为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中，Y代表因变量，X1，X2，...，Xn代表自变量，β0，β1，β2，...，βn为待估计的回归系数，ε为随机误差项。

二、多元线性回归模型的估计方法为了确定回归系数的最佳估计值，常采用最小二乘法进行估计。

最小二乘法的原理是使残差平方和最小化，从而得到回归系数的估计值。

具体求解过程包括对模型进行估计、解释回归系数、进行显著性检验和评价模型拟合度等步骤。

三、多元线性回归模型的假设条件为了保证多元线性回归模型的准确性和可靠性，需要满足一定的假设条件。

主要包括线性关系、多元正态分布、自变量之间的独立性、无多重共线性、残差项的独立性和同方差性等。

在实际应用中，我们需要对这些假设条件进行检验，并根据检验结果进行相应的修正。

四、多元线性回归模型的应用多元线性回归模型广泛应用于各个领域的研究和实践中。

在经济学中，可以用于预测国内生产总值和通货膨胀率等经济指标；在市场营销中，可以用于预测销售额和用户满意度等关键指标；在医学研究中，可以用于评估疾病风险因素和预测治疗效果等。

多元线性回归模型的应用可以为决策提供科学依据，并帮助解释变量对因变量的影响程度。

五、多元线性回归模型的优缺点多元线性回归模型具有以下优点：1）能够解释各个自变量对因变量的相对影响；2）提供了一种可靠的预测方法；3）可用于控制变量的效果。

然而，多元线性回归模型也存在一些缺点：1）对于非线性关系无法准确预测；2）对异常值和离群点敏感；3）要求满足一定的假设条件。

Stata多元线性回归模型建立及检验——关于这篇笔记，有的人嘴上说着不想写，下笔实际上很快乐。

第一步导入excel文件clear #清除所有变量 cd D:\stata_data #数据保存的地址 import excel sample.xlsx, firstrow #导入数据，文件名为sample.xlsx，把第一行作为变量名 tsset t#建立时间序列若不存在时间变量可忽略此处以x1,x2,x3,x3作为自变量，y作为因变量，t为时间变量。

若需建立对数模型，则可利用generate生成新变量。

generate logy = log10(y)#生成变量名为logy的新变量第二步多变量线性回归regress y x1 x2 x3#对模型进行最小二乘法估计运行结果回归方程：第三步多重共线性检验estat vif#方差扩大因子法检验当VIF≥10，则认为自变量之间有严重的多重共线性。

运行结果若模型出现多重共线性，可以剔除一些不重要的解释变量，或增大样本量。

第四步异方差检验imtest,white#White检验如果输出的P-Value显著小于0.05，则拒绝原假设，认为存在异方差性。

运行结果若模型出现异方差性，则不能用普通的最小二乘法进行估计，需要对原模型进行变换，使之满足同方差性假设，然后进行模型参数估计。

通常可以采用加权最小二乘法（weighted least square,WLS）或BOX-COX变换法。

第五步序列相关性检验首先保证所用的数据必须为时间序列数据。

如果原数据不是时间序列数据，则需要自行定义一个：gen n=_n #生成一个时间序列的标志变量ntsset n #将这个数据集定义为依据时间序列标志变量n定义的时间序列数据接下来介绍三种检验方法（一）残差图检验predict e,r#生成残差值e scatter eLe#生成残差散点图运行结果（二）DW检验（一阶自相关问题的常用检验法）estat dwatson#DW检验经验上，DW值在1.8-2.2之间时接受原假设，说明模型不存在一阶自相关，若DW值接近0或4，则拒绝原假设，认为存在一阶自相关。

stata多元回归代码1. 简介Stata 是一个用于数据分析和统计建模的软件，它拥有强大的多元回归分析功能。

通过在 Stata 中编写多元回归代码，可以进行数据挖掘，预测模型构建等应用，从而发现数据背后的规律。

2. 数据准备在编写多元回归代码之前，我们需要先准备好所需的数据。

可以使用Stata 自带的数据集，也可以使用外部数据集。

数据集需要满足以下要求：- 包含完整的变量信息；- 无缺失值或具有较少的缺失值；- 数据类型正确。

在此，我们以 Stata 自带的 auto 数据集为例进行讲解。

auto 数据集包含了关于汽车的相关信息，我们将使用 mpg、weight、length 等变量来建立多元回归模型，预测汽车的燃油效率（mpg）。

3. 多元回归模型多元回归模型是一种用于分析多个自变量与一个因变量之间关系的方法。

通常，多元回归模型可以表示为：Y = β0 + β1X1 + β2X2 + … + βnXn + ε其中，Y 表示因变量（即待预测的 mpg），Xi 表示自变量（如weight、length 等），βi 表示自变量的系数，ε 表示误差项。

4. 代码实现在 Stata 中，我们可以通过命令行输入以下代码来建立多元回归模型：regress mpg weight length其中，mpg 是因变量，weight 和 length 是自变量。

如果我们需要加入更多自变量，可以在命令中继续添加：regress mpg weight length displacement在执行完以上代码后，Stata 会自动输出多元回归模型的结果，包括模型的拟合优度（R-squared）、各自变量的系数、标准误差、t 值、p 值等信息。

5. 结论通过 Stata 编写多元回归代码，我们可以快速构建预测模型，并通过各种统计分析方法对模型进行进一步分析和优化。

通过对多元回归模型的研究，我们可以更好地了解各自变量对因变量的影响，进而优化模型，提高预测精度。

《计量经济学》教学大纲一、课程基本信息课程名称：计量经济学课程类别：专业核心课课程学分：＿____学分课程总学时：＿____学时授课对象：＿____专业学生二、课程性质与教学目的（一）课程性质计量经济学是一门融合了经济学、统计学和数学的交叉学科，是现代经济学的重要组成部分。

它运用数学和统计学方法，通过建立经济计量模型来定量分析经济变量之间的关系，为经济决策提供实证依据。

（二）教学目的1、使学生掌握计量经济学的基本理论和方法，包括经典线性回归模型、多元回归模型、异方差、自相关、多重共线性等问题的处理方法。

2、培养学生运用计量经济学方法分析和解决实际经济问题的能力，能够独立建立经济计量模型，并进行模型的估计、检验和应用。

3、提高学生的逻辑思维能力和数据分析能力，为进一步学习和研究经济学及相关领域打下坚实的基础。

三、课程教学要求1、学生应具备扎实的经济学、数学和统计学基础知识，如微观经济学、宏观经济学、概率论、数理统计等。

2、学生应按时完成课程作业，积极参与课堂讨论和案例分析，主动思考和解决问题。

3、学生应掌握至少一种计量经济学软件，如 EViews、Stata 等，能够运用软件进行数据处理和模型估计。

四、课程教学内容（一）绪论1、计量经济学的定义、研究内容和发展历程2、计量经济学的研究步骤和方法3、计量经济学模型的分类和应用领域（二）经典线性回归模型1、线性回归模型的基本假设2、最小二乘法估计参数3、模型的统计检验，包括拟合优度检验、t 检验和 F 检验4、预测和区间估计（三）多元线性回归模型1、多元线性回归模型的形式和假设2、模型参数的估计和检验3、多重共线性问题及其处理方法4、变量的选择和逐步回归法（四）异方差1、异方差的概念和产生原因2、异方差的检验方法，如 White 检验、GoldfeldQuandt 检验等3、异方差的修正方法，如加权最小二乘法（五）自相关1、自相关的概念和产生原因2、自相关的检验方法，如 DW 检验、BG 检验等3、自相关的修正方法，如广义差分法（六）虚拟变量1、虚拟变量的概念和设置原则2、包含虚拟变量的回归模型3、虚拟变量的交互作用（七）滞后变量模型1、滞后变量模型的类型和特点2、分布滞后模型的估计方法3、自回归模型的估计和应用（八）联立方程模型1、联立方程模型的概念和类型2、联立方程模型的识别问题3、联立方程模型的估计方法，如间接最小二乘法、两阶段最小二乘法等（九）时间序列分析1、时间序列的平稳性和单位根检验2、协整分析和误差修正模型3、时间序列模型，如 ARMA 模型、ARIMA 模型等（十）计量经济学应用案例分析1、经济增长、通货膨胀、就业等宏观经济问题的计量分析2、消费、投资、进出口等微观经济问题的计量分析五、课程教学方法1、课堂讲授：讲解计量经济学的基本理论和方法，通过实例分析加深学生对知识点的理解。

stata多元回归分析stata多元回归分析Stata多元回归分析主要包括基本回归分析、对函数形式的进一步讨论（对数、二次项、交互项）、含有虚拟变量的模型、异方差四个方面。

高斯—马尔可夫定理在给定经典线性回归的假定下，最小二乘估计量是具有最小方差的线性无偏估计量。

MLR.1线性模型MLR.2样本是随机抽样得出的MLR.3不存在完全共线性MLR.4条件均值为零，给定自变量的任何值误差μ的期望为零，即E(u/X1,X2...Xk)=0MLR.5同方差，给定任意解释变量值，误差μ的方差相同，即Var(u/X1,X2...Xk)=σ21.基本回归分析以计量经济学导论（第五版）第四章第2小题为例，数据为LAWSCH85.DTA，刚从法学院毕业的学生的起薪中位数由下式决定：log(salary)=b0+b1LSAT+b2GPA+b3log(libvol)+b4log(cost) +b5rank+ u其中，LSAT是整个待毕业年级LSAT成绩的中位数，GPA是该年级大学GPA的中位数，libvol是法学院图书馆藏书量，cost是法学院每年的费用，rank是法学院的排名。

(i)检验原假设H0：rank对法学院毕业生起薪中位数没有影响。

(ii)检验LSAT和GPA是否联合显著，H0：βLSAT=βGPA=0估计方程的命令为：reg lsalary LSAT GPA llibvol lcost rank估计结果为：log(salary)=58.34+0.004LSAT+0.24GPA+0.095lg(libvol)+0.038log(cost)-0.0033rankn=136,R2=0.842.(i)H0：βrank=0，t统计量=b/se(b)，即系数/标准误trank=-0.0033/0.00035=-9.54，P值=0，rank即使在1%的显著性水平上都是统计显著的，拒绝原假设H0.①t检验命令：test rank(ii)T检验可以看出GPA即使在1%的水平下也是显著的，而LSAT 即使在10%的水平下也不显著，联合检验LSAT和GPA对法学院毕业生起薪中位数是否有影响。

stata估计回归方程Stata是一种广泛使用的统计软件，可用于估计回归方程。

回归分析是一种数据分析技术，可用于确定两个或多个变量之间的关系。

回归模型旨在解释响应变量（也称为因变量）和自变量（也称为解释变量）之间的关系。

在Stata中，可以使用命令reg命令来估计简单线性回归模型和多元线性回归模型。

在本文中，我们将讨论如何使用Stata估计回归方程。

一、简单线性回归方程简单线性回归方程是一种使用单个自变量解释响应变量的回归模型。

下面是一个示例，其中Y是响应变量，X是解释变量。

Y = β0 + β1X + ε其中，Y：响应变量X: 解释变量β0和β1：回归系数ε：误差项在Stata中，可以使用以下代码估计简单线性回归方程：reg y x这将生成以下输出：------------------------------------------------------------------------------y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+----------------------------------------------------------------x | .4534248 .0153275 29.580.000 .4223481 .4845014_cons | 3.117376 .3083924 10.10 0.000 2.493708 3.741044------------------------------------------------------------------------------在这个输出中，.453424是解释变量X的回归系数，表明在解释变量每增加1个单位的情况下，响应变量Y预计增加0.453424个单位。

_cons给出截距，表示在解释变量为零时的响应变量。

stata中回归知识点总结简单线性回归简单线性回归是回归分析中最基本的形式。

它用于研究一个自变量对一个因变量的影响。

在Stata中进行简单线性回归可以使用reg命令。

比如，我们有一个数据集包含了两个变量x和y，我们想知道x对y的影响，可以使用如下命令进行简单线性回归：```reg y x```这条命令将会输出回归方程的拟合结果，包括截距项和自变量系数。

多元线性回归多元线性回归是回归分析中更常见的形式。

它用于研究多个自变量对一个因变量的影响。

在Stata中进行多元线性回归同样可以使用reg命令。

比如，我们有一个数据集包含了三个变量x1、x2和y，我们想知道x1和x2对y的影响，可以使用如下命令进行多元线性回归：```reg y x1 x2```逻辑回归逻辑回归是用来处理因变量为二值变量的回归分析方法。

在Stata中进行逻辑回归可以使用logit命令。

比如，我们有一个数据集包含了两个变量x和y，其中y是一个二值变量（比如0和1），我们想知道x对y的影响，可以使用如下命令进行逻辑回归：```logit y x```高级回归技巧除了上述的基本回归分析方法，Stata还提供了许多高级的回归技巧，比如假设检验、多重共线性检验、残差分析等。

其中，假设检验是用来检验回归模型的显著性，通常使用命令test。

多重共线性检验是用来检验自变量之间的相关性，通常使用命令collin。

残差分析是用来检验模型的拟合情况，通常使用命令predict和rvfplot。

总结回归分析是统计学中常用的一种分析方法，它用于研究自变量和因变量之间的关系。

在Stata中，回归分析是一种非常常见的数据分析方法，包括简单线性回归、多元线性回归、逻辑回归和一些高级回归技巧。

希望本文对Stata用户们有所帮助。