3.2.3利用法向量求二面角

3.2向量法求二面角(16-1)编制人：闵小梅 审核人：王志刚【使用说明及学法指导】 1.完成预习案中的相关问题；2.尝试完成探究案中合作探究部分，注意书写规范；3.找出自己的疑惑和需要讨论的问题准备课堂讨论质疑。

【学习目标】会用法向量求二面角的大小 【教学重点】向量法求二面角的大小【教学难点】建立适当的坐标系，准确写出点的空间坐标 一、复习引入 【复习】知识点1．向量法求两条异面直线所成的角（范围：]2,0(πθ∈）|||||,cos |cos n m=><=θ知识点2．向量法求直线与平面所成角（范围：[θ∈sin |cos ,|n AB θ=<>=r uu u r类比以上求法，思考如何用向量法求二面角？ 回顾二面角的有关概念： (1) 二面角的定义平面内的一条直线把平面分成两部分，其中的每一部分都叫做半平面，从一条直线出发的两个半平面所组成的图形叫做二面角。

(2)二面角的平面角①过二面角的棱上的一点O 分别在两个半平面内作棱的两条垂线,OA OB ，则AOB ∠叫做二面角l αβ--的平面角，[0,]AOB π∠∈。

②一个平面垂直于二面角l αβ--的棱l ，且与两半平面交线分别为,,OA OB O 为垂足，则AOB ∠也是l αβ--的平面角，[0,]AOB π∠∈。

abαθO12）【引入】知识点3．向量法求二面角（范围：[0,]θπ∈）①方向向量法：将二面角转化为二面角的两个面的方向向量（在二面角的面内且垂直于二面角的棱）的夹角。

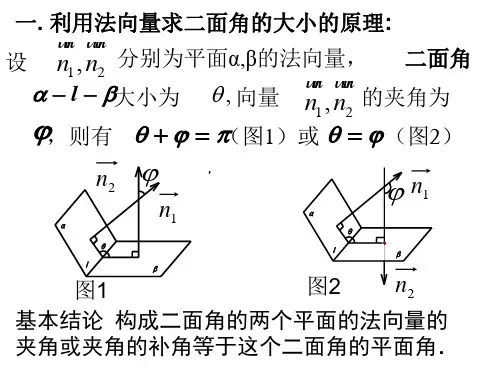
如图，设二面角βα--l 的大小为θ，其中βα⊂⊥⊂⊥CD l CD AB l AB ,,,.结论：②法向量法如图1、2所示时，二面角l αβ--的平面角与平面α、β的法向量1n r ，2n r的夹角12,n n <>r r相等，即 ；如图3、4所示时，二面角l αβ--的平面角与平面α、β的法向量1n r ，2n r的夹角12,n n <>r r相等，即结论：cos θ＝ 或 cos θ＝二面角l αβ--为锐二面角时，cos θ＝二面角l αβ--为钝二面角时，cos θ＝ 【尝试练习】1.已知两平面的法向量分别为1n r =（0，1，0），2n r=（0，1，3）,则两平面所成的二面角余弦值为____ 2．（课本P107练习2改编）二面角的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于AB 。

求二面角的方法求二面角的方法二面角是一个非常重要的概念，在数学、物理、化学等领域都有广泛的应用。

它是指两个平面或曲面之间的夹角，也可以理解为一个三维图形中相邻两个面之间的夹角。

在这里，我们将介绍几种求二面角的方法。

方法一：向量法向量法是一种比较简单易懂的方法。

首先，我们需要找到两个平面或曲面上的法向量，然后计算它们之间的夹角即可得到二面角。

具体步骤如下：1. 找到两个平面或曲面上的法向量。

2. 计算这两个法向量之间的夹角，可以使用余弦定理或内积公式进行计算。

3. 将得到的结果转换为度数制即可得到二面角。

例如，假设我们要求一个正四棱锥中底面和侧棱所在平面之间的二面角。

首先，我们需要找到底面和侧棱所在平面上的法向量。

底面上任意一点处垂直于底面且指向外部的单位法向量为(0,0,-1)，而侧棱所在平面上任意一点处垂直于该平面且指向内部的单位法向量为(1/√2,0,-1/√2)。

然后，我们可以使用余弦定理计算它们之间的夹角，即cosθ=（0×1/√2+0×0+（-1）×（-1/√2））÷（√（0²+0²+1²）×√（（1/√2）²+0²+（-1/√2）²）），得到cosθ=1/3。

将其转换为度数制，即θ≈70.53°，即可得到二面角。

方法二：三角形面积法三角形面积法是另一种求解二面角的方法。

它需要先求出相邻两个面所在平面上的三个顶点，然后计算这三个顶点构成的三角形面积，最后根据正弦定理求出二面角。

具体步骤如下：1. 找到相邻两个面所在平面上的三个顶点。

2. 计算这三个顶点构成的三角形的面积。

3. 根据正弦定理计算出二面角。

例如，假设我们要求一个立方体中相邻两个正方形所在平面之间的二面角。

首先，我们需要找到这两个正方形所在平面上的三个顶点。

可以选择其中一个正方形上任意一点作为第一个顶点，然后在该正方形上选择任意两个相邻的点作为第二和第三个顶点。

空间向量与空间角(30分钟50分)一、选择题(每小题3分,共18分)1.在矩形ABCD中,AB=1,BC=,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成角是( )A.30°B.45°C.60°D.90°【解析】选 A.建立如图所示的空间直角坐标系,则P(0,0,1),C(1,,0),=(1,,-1),平面ABCD的一个法向量为n=(0,0,1),所以cos<,n>==-,所以<,n>=120°,所以斜线PC与平面ABCD的法向量所在直线所成角为60°,所以斜线PC与平面ABCD所成角为30°.2.(2014²重庆高二检测)设ABCD,ABEF都是边长为1的正方形,FA⊥平面ABCD,则异面直线AC与BF所成的角等于( )A.45°B.30°C.90°D.60°【解析】选D.以B为原点,BA所在直线为x轴,BC所在直线为y轴,BE所在直线为z轴建立空间直角坐标系,则A(1,0,0),C(0,1,0),F(1,0,1),所以=(-1,1,0),=(1,0,1).所以cos<,>=-.所以<,>=120°.所以AC与BF所成的角为60°.3.把正方形ABCD沿对角线AC折起成直二面角,点E,F分别是AD,BC的中点,O是正方形中心,则折起后,∠EOF的大小为( )A. B. C. D.【解析】选C.=(+),=(+),所以²=(²+²+²+²)=-||2.又||=||=||,所以cos<,>==-.所以∠EOF=.4.在直角坐标系中,已知A(2,3),B(-2,-3),沿x轴把直角坐标系折成平面角为θ的二面角A-Ox-B,使∠AOB=90°,则cosθ为( )A.-B.C.D.-【解析】选C.过A,B分别作x轴垂线,垂足分别为A′,B′.则AA′=3,BB′=3,A′B′=4,OA=OB=,折后∠AOB=90°,所以AB==.由=++,得||2=||2+||2+||2+2||²||²cos(π-θ).所以26=9+16+9+2³3³3³cos(π-θ),所以cosθ=.5.(2014²天津高二检测)在正方体ABCD-A1B1C1D1中,E是C1C的中点,则直线BE与平面B1BD所成的角的正弦值为( )A.-B.C.-D.【解析】选B.建立如图所示的空间直角坐标系,设正方体的棱长为2,则D(0,0,0),B(2,2,0),B1(2,2,2),E(0,2,1).所以=(-2,-2,0),=(0,0,2),=(-2,0,1).设平面B1BD的法向量为n=(x,y,z).因为n⊥,n⊥,所以所以令y=1,则n=(-1,1,0).所以cos<n,>==,设直线BE与平面B1BD所成角为θ,则sinθ=|cos<n,>|=.6.如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )A. B. C. D.【解析】选C.如图,以A为原点建立空间直角坐标系,则A(0,0,0),B(0,2a,0),C(0,2a,2a),G(a,a,0),F(a,0,0),=(a,a,0),=(0,2a,2a),=(a,-a,0),=(0,0,2a),设平面AGC的法向量为n1=(x1,y1,1),由⇒⇒⇒n1=(1,-1,1).sinθ===.二、填空题(每小题4分,共12分)7.(2014²唐山高二检测)平面α的一个法向量为(1,0,-1),平面β的一个法向量为(0,-1,1),则平面α与平面β所成二面角的大小为.【解析】设u=(1,0,-1),v=(0,-1,1),平面α与平面β所成二面角为θ,则cosθ=±|cos<u,v>|=±||=±.所以θ=或.答案:或8.正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1C1的中点,则异面直线AE与CF所成角的余弦值为 . 【解析】设正方体棱长为2,分别取DA,D C,DD1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系, 则A(2,0,0),C(0,2,0),E(1,0,2),F(1,1,2),则=(-1,0,2),=(1,-1,2),所以||=,||=.²=-1+0+4=3.又²=||||cos<,>=cos<,>,所以cos<,>=,所以所求角的余弦值为.答案:【变式训练】已知在棱长为a的正方体ABCD-A′B′C′D′中,E是BC的中点.则直线A′C与DE所成角的余弦值为.【解析】建立如图所示的空间直角坐标系,则A′(0,0,a),C(a,a,0),D(0,a,0),E,=(a,a,-a),=,所以cos<,>==.即直线A′C与DE所成角的余弦值为.答案:9.(2014²福州高二检测)在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D,E,F分别是棱AB,BC,CP的中点,AB=AC=1,PA=2,则直线PA与平面DEF所成角的正弦值为.【解析】以A为原点,AB,AC,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,由AB=AC=1,PA=2,得A(0,0,0),B(1,0,0),C(0,1,0),P(0,0,2), D, E,F,所以=(0,0,2),=,=,设平面DEF的法向量n=(x,y,z). 则由得取z=1,则n=(2,0,1),设PA与平面DEF所成角为θ,则sinθ==.答案:【变式训练】在正方体ABCD-A1B1C1D1中,直线BC1与平面A1BD所成角的余弦值是. 【解析】建立如图所示的空间直角坐标系,设棱长为1,则B(1,1,0),C1(0,1,1),A1(1,0,1),D(0,0,0),=(-1,0,1),=(-1,0,-1),=(-1,-1,0),设平面A1BD的一个法向量为n=(1,x,y),设平面A1BD与BC1所成的角为θ,n⊥,n⊥,所以n²=0,n²=0,所以解得所以n=(1,-1,-1),则cos<,n>==-,所以sinθ=,所以cosθ==.答案:三、解答题(每小题10分,共20分)10.(2014²临沂高二检测)四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,CD=4,E,F分别为CD,PB的中点.(1)求证:EF⊥平面PAB.(2)求直线AE与平面PAB所成的角.【解析】(1)建立如图所示空间直角坐标系Dxyz,则E(0,-2,0),F(1,-2,1),P(0,0,2),A(2,0,0),B(2,-4,0),所以=(1,0,1),=(0,-4,0),=(2,0,-2),所以²=(1,0,1)²(0,-4,0)=0,²=(1,0,1)²(2,0,-2)=0,所以⊥,⊥,所以EF⊥AB,EF⊥PA,因为AB⊂平面PAB,PA⊂平面PAB,AB∩PA=A,所以EF⊥平面PAB.(2)=(1,0,1)是平面PAB的一个法向量,设直线AE与平面PAB所成的角为θ,因为=(-2,-2,0),所以sinθ===,所以直线AE与平面PAB所成的角是30°.【变式训练】在正方体ABCD-A1B1C1D1中,E,F分别为AA1,AB的中点,求EF和平面ACC1A1夹角的大小. 【解析】建立如图所示的空间直角坐标系,设正方体棱长为2,则由E,F分别是AA1,AB的中点,得E(2,0,1),F(2,1,0).过F作FG⊥AC于G,则由正方体性质知FG⊥平面ACC1A1.连接EG,则与的夹角即为所求.又因为F是AB的中点,所以AG=AC,所以G.=,=(0,1,-1),cos<,>==.所以<,>=,即EF与平面ACC1A1的夹角为.【一题多解】建系同上,=(0,1,-1),A1(2,0,2),A(2,0,0),C(0,2,0),=(0,0,-2),=(-2,2,0).设平面ACC1A1的法向量为n=(x,y,z),则即令x=1,则y=1,所以n=(1,1,0),cos<n,>===.所以<n,>=,则EF与平面ACC1A1的夹角为.11.在正方体ABCD-A1B1C1D1中,E,F分别为棱D1C1,B1C1的中点,求平面EFC与底面ABCD所成二面角的正切值. 【解析】以D为原点,{,,}为单位正交基底建立空间直角坐标系如图,则C(0,1,0),E,F.设平面CEF的法向量为n=(x,y,z),则因为=,=,所以所以令z=1,则n=(-2,2,1).显然平面ABCD的法向量e=(0,0,1),则cos<n,e>==.设二面角为α,则cosα=,所以tanα=2.【拓展延伸】向量法求解二面角时的注意点由于两条直线所成的角,线面角都是锐角或直角,因此可直接通过绝对值来表达,故可直接求出,而二面角的范围是[0,π],有时比较难判断二面角是锐角还是钝角,因为不能仅仅由法向量夹角余弦的正负来判断,故这是求二面角的难点.(30分钟50分)一、选择题(每小题4分,共16分)1.已知向量m,n分别是直线l和平面α的方向向量和法向量,若cos<m,n>=-,则l与α所成的角θ为( )A.30°B.45°C.135°D.150°【解析】选B.因为cos<m,n>=-,所以sinθ=|cos<m,n>|=.又因为直线与平面所成角θ满足0°≤θ≤90°,所以θ=45°.2.(2014²长春高二检测)在长方体ABCD-A1B1C1D1中,AB=2,BC=2,DD1=3,则AC与BD1所成角的余弦值为( )A.0B.C.-D.【解析】选A.建立如图坐标系,则D1(0,0,3),B(2,2,0),A(2,0,0),C(0,2,0),所以=(-2,-2,3),=(-2,2,0).所以cos<,>==0.所以<,>=90°,所求角的余弦值为0.【变式训练】如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM 所成的角的大小是.【解析】不妨设棱长为2,则=-,=+,cos<,>==0,故异面直线AB1和BM所成角为90°.答案:90°3.(2014²哈尔滨高二检测)在正四棱锥S-ABCD中,O为顶点在底面内的投影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角是( )A.30°B.45°C.60°D.75°【解析】选A.如图,以O为坐标原点建立空间直角坐标系Oxyz.设OD=SO=OA=OB=OC=a,则A(a,0,0),B(0,a,0),C(-a,0,0),P,则=(2a,0,0),=,=(a,a,0),设平面PAC的一个法向量为n,可取n=(0,1,1),则cos<,n>===,所以<,n>=60°,所以直线BC与平面PAC的夹角为90°-60°=30°.4.(2014²南宁高二检测)如图所示,已知点P为菱形ABCD外一点,且PA⊥平面ABCD,PA=AD=AC,点F为PC 的中点,则二面角C-BF-D的正切值为( )A. B. C. D.【解析】选D.如图所示,连接BD,AC∩BD=O,连接OF.以O为原点,OB,OC,OF所在直线分别为x,y,z轴建立空间直角坐标系Oxyz.设PA=AD=AC=1,则BD=.所以B,F,C,D.结合图形可知,=且为面BOF的一个法向量,由=,=,可求得平面BCF的一个法向量n=.所以cos<n,>=,sin<n,>=,所以tan<n,>=.二、填空题(每小题5分,共10分)5.正△ABC与正△BCD所在平面垂直,则二面角A-BD-C的正弦值为.【解析】取BC中点O,连接AO,DO,建立如图所示的坐标系:设BC=1,则A,B,D.所以=,=,=.由于=为平面BCD的一个法向量,设平面ABD的法向量n=(x,y,z),则所以取x=1,则y=-,z=1,所以n=(1,-,1),所以cos<n,>=,sin<n,>=.答案:6.(2014²湛江高二检测)如图,在正三棱柱ABC-A1B1C1中,若AB=BB1,则AB1与C1B所成的角的大小为.【解题指南】根据正三棱柱的特点建立空间直角坐标系,再用向量法求异面直线所成的角.【解析】取AC的中点D,建立如图坐标系,设AB=a,则B,C1,A,B1.所以=,=.所以cos<,>==0.所以AB1与C1B所成的角为90°.答案:90°三、解答题(每小题12分,共24分)7.(2013²新课标全国卷Ⅰ)如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(1)证明AB⊥A1C.(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.【解题指南】(1)取AB的中点,利用线面垂直证明线线垂直.(2)利用面面垂直确定线面垂直,找出直线A1C与平面BB1C1C所成的角或建立空间直角坐标系求解. 【解析】(1)取AB的中点O,连结OC,OA1,A1B.因为CA=CB,所以OC⊥AB.由于AB=AA1,∠BAA1=60°,故△AA1B为等边三角形,所以OA1⊥AB.因为OC∩OA1=O,所以AB⊥平面OA1C.又A1C⊂平面OA1C,故AB⊥A1C.(2)由(1)知,OC⊥AB,OA1⊥AB,又平面ABC⊥平面AA1B1B,交线为AB,所以OC⊥平面AA1B1B,故OA,OC,OA1两两相互垂直. 以O为坐标原点,的方向为x轴的正方向,||为单位长度,建立如图所示的空间直角坐标系Oxyz,则有A(1,0,0),A1(0,,0),C(0,0,),B(-1,0,0).则=(1,0,),==(-1,,0),=(0,-,).设平面BB1C1C的法向量为n=(x,y,z),则有即可取n=(,1,-1).故cos<n,>==-.所以直线A1C与平面BB1C1C所成角的正弦值为.【变式训练】(2013²辽宁高考)如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.(1)求证:平面PAC⊥平面PBC.(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.【解题指南】利用条件证明线线垂直,进而证明线面垂直,由面面垂直的判定定理解决问题;借助前面的垂直关系,建立空间直角坐标系,利用向量法求二面角的余弦值.【解析】(1)由AB是圆的直径,得AC⊥BC;由PA垂直于圆所在的平面,得PA⊥平面ABC;由BC⊂平面ABC,得PA⊥BC;又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.又因为BC⊂平面PBC,据面面垂直判定定理,平面PAC⊥平面PBC.(2)过点C作CM∥AP,由(1)知CM⊥平面ABC.如图所示,以点C为坐标原点,分别以直线CB,CA,CM为x,y,z轴,建立空间直角坐标系.在直角三角形ABC中,AB=2,AC=1,所以BC=,又PA=1,所以A(0,1,0),B(,0,0),P(0,1,1).故=(,0,0),=(0,1,1).设平面PBC的法向量为n1=(x1,y1,z1),则⇒⇒不妨令y1=1,则z1=-1.故n1=(0,1,-1).设平面PAB的法向量为n2=(x2,y2,z2),由同理可得n2=(1,,0).于是cos<n1,n2>===.结合图形和题意,二面角C-PB-A的余弦值为.8.(2014²山东高考)如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.(1)求证:C1M∥平面A1ADD1.(2)若CD1垂直于平面ABCD且CD1=,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.【解题指南】(1)本题考查了线面平行的证法,可利用线线平行来证明线面平行.(2)本题可利用空间几何知识求解二面角,也可以利用向量法来求解.【解析】(1)连接AD1,因为ABCD-A1B1C1D1为四棱柱,所以CD∥C1D1,CD=C1D1,又因为M为AB的中点,AB=2CD=2,所以AM=1,所以CD∥AM,CD=AM,所以AM∥C1D1,AM=C1D1,所以四边形AMC1D1为平行四边形,所以AD1∥MC1,又因为C1M⊄平面A1ADD1,AD1⊂平面A1ADD1,所以C1M∥平面A1ADD1.(2)方法一:因为AB∥A1B1,A1B1∥C1D1,所以平面D1C1M与ABC1D1共面,作CN⊥AB,连接D1N,则∠D1NC即为所求二面角的平面角.在ABCD中,DC=1,AB=2,∠DAB=60°,所以CN=,在Rt△D1CN中,CD1=,CN=,所以D1N=,cos∠D1NC==.方法二:作CP⊥AB于P点,以C为原点,CD为x轴,CP为y轴,CD1为z轴建立空间直角坐标系, 所以C1(-1,0,),D1(0,0,),M,所以=(1,0,0),=,设平面C1D1M的法向量为n1=(x1,y1,z1),所以所以n1=(0,2,1),显然平面ABCD的法向量为n2=(0,0,1),所以cos<n1, n2>===.显然二面角为锐角,所以平面C1D1M和平面ABCD所成的角的余弦值为.【变式训练】如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.(1)求证:A1B∥平面ADC1.(2)求二面角C1-AD-C的余弦值.(3)试问线段A1B1上是否存在点E,使AE与DC1成60°角?若存在,确定E点位置;若不存在,说明理由. 【解析】(1)连接A1C,交AC1于点O,连接OD.由ABC-A1B1C1是直三棱柱,得四边形ACC1A1为矩形,O为A1C的中点.又D为BC的中点,所以OD为△A1BC的中位线,所以A1B∥OD,因为OD⊂平面ADC1,A1B⊄平面ADC1,所以A1B∥平面ADC1.(2)由ABC-A1B1C1是直三棱柱,且∠ABC=90°,得BA,BC,BB1两两垂直.以BC,BA,BB1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系Bxyz.设BA=2,则B(0,0,0),C(2,0,0),A(0,2,0),C1(2,0,1),D(1,0,0),所以=(1,-2,0),=(2,-2,1).设平面ADC1的法向量为n=(x,y,z),则有所以取y=1,得n=(2,1,-2).易知平面ADC的一个法向量为v=(0,0,1).所以cos<n,v>==-.因为二面角C1-AD-C是锐二面角,所以二面角C1-AD-C的余弦值为.(3)假设存在满足条件的点E.因为点E在线段A1B1上,A1(0,2,1),B1(0,0,1),故可设E(0,λ,1),其中0≤λ≤2.所以=(0,λ-2,1),=(1,0,1).因为AE与DC1成60°角,所以|cos<,>|==.即=,解得λ=1或λ=3(舍去).所以当点E为线段A1B1的中点时,AE与DC1成60°角.。

法向量求二面角余弦值公式
在数学的背景下，对于求解任意两向量夹角的余弦值，法向量求二面角余弦值公式是一个有效的方法。

法向量是一种在三维空间中的有向线段，它可以用来表示一个面的法线，即以该面上任一点为原点，以该面的法线方向为方向的有向线段。

法向量求二面角余弦值公式可以用来求解这样一种问题：对于两个法向量n1n2，求取它们之间所构成的角的余弦值。

为此，我们需要引入一个新的变量，即角α，这个角以度为单位进行计算。

根据法向量求二面角余弦值公式，如下所示：
cosα＝n1n2/（|n1|*|n2|）
这里，n1和n2分别表示两个法向量，而|n1|和|n2|则表示n1
和n2这两个向量的模，即沿着向量方向的长度。

说起来，这个法向量求二面角余弦值公式其实非常简单，其运用也十分广泛，它不仅仅可以被用来计算任意两个法线之间的夹角，而且还可以被用来计算任意三维空间中两个向量之间的夹角。

以下给出一个具体的例子，来验证一下法向量求二面角余弦值公式的正确性。

假设n1=[1,2,3]，n2=[1,0,1]，那么我们可以使用法向量求二面角余弦值公式来计算n1和n2之间的夹角。

首先计算n1和n2的模，即|n1|=√(1^2+2^2+3^2)=√14，|n2|=√(1^2+0+1^2)=√2，接着，我们可以计算n1n2=1*1+2*0+3*1=4，最后，将公式中所有的变量进行替换，最终求得cosα＝4/（√14*√2）=0.8333…
以上，就是法向量求二面角余弦值公式的基本概念及其具体使用的例子。

总结一下，法向量求二面角余弦值公式是一种非常实用的数学方法，它可以帮助我们快速求出任意两个法向量之间的夹角余弦值，从而让我们有更清晰的认知。

法向量求二面角余弦值公式法向量求二面角余弦值公式是用来求解三维空间中两个不同方向的法向量之间的夹角的余弦值的一种公式。

它是一种有用的工具，可以用来计算夹角的大小，以及两个法向量之间的方向性。

首先，什么是法向量？法向量是一种特殊的二维向量，它的分量指示着从一个坐标到另一个坐标的方向，但它不指示距离。

它一般用来描述平面或曲面的方向，如平面的法向量指向的是平面的法线方向。

接下来，我们来看一下公式本身。

法向量求二面角余弦值公式是： cosθ = n 1n 2 /（ | n 1 | | n 2 |其中表示两个法向量的夹角，n 1 n 2别表示两个不同方向的法向量，| n 1 | | n 2 |别表示其向量长度。

从上面的公式可以看出，计算两个法向量之间的余弦值需要一些数学知识，尤其是矢量代数方面的知识。

如果没有深入理解它的相关内容，可能会遇到一些困难。

然而，这种公式也是一个非常有用的工具，因为它可以求出任意两个法向量之间的夹角。

在可视化和空间模型中，它可以让我们快速准确地计算出两个法向量之间的夹角。

比如，在建筑中，我们需要精确测量出梁的弯曲角度，这时就可以用法向量求二面角余弦值公式来计算。

另外，在数字图像处理中，如果我们想要知道两个不同方向上的像素之间的夹角，那么也可以利用这种公式来求解。

此外，在机器学习中，当我们需要测量两个特征向量之间的角度时，也同样可以用这种公式来计算。

例如，在自然语言处理（NLP）任务中，我们可以用它来判断两个字的相似程度。

总之，法向量求二面角余弦值公式是一种有益的工具，它可以让我们快速准确地计算出任意两个不同方向的法向量之间的夹角余弦值。

它在许多不同的应用领域中都有用，比如建筑，数字图像处理，机器学习，以及自然语言处理，等等。

因此，这种公式可以说是在不同学科中都很有用，是三维空间中两个不同方向的法向量之间夹角余弦值求解的有效方法。

3.2.3向量法求空间距离根据两向量数量积的性质和坐标运算，利用公式或(其中) ，可将两点距离问题转化为求向量模长问题【例1】如图1：一个结晶体的形状为四棱柱，其中，以顶点A为端点的三条棱长都相等，且它们彼此的夹角都是60°，那么以这个顶点为端点的晶体的对角线的长与棱长有什么关系？变式练习如图，60°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直AB，已知AB＝4，AC＝6，BD＝8，求CD的长.变式练习如图所示，在平行四边形ABCD中，AB＝AC＝1，∠ACD＝90°，将它沿对角线AC折起，使AB与CD成60°角，求B、D间的距离．[题后感悟] 求空间中两点间距离的主要方法(1)建立空间直角坐标系，求出两点的坐标，代入两点间距离公式求解；(2)将以两点为端点的向量用基向量表示，再求此向量如图A ,α∈空间一点P 到平面α的距离为d ,已知平面α的一个法向量为n ,且AP 与n 不共线,能否用AP 与n 表示d ?例2: 如图，已知正方形ABCD 的边长为4，E 、F 分别是AB 、AD 的中点，GC ⊥平面ABCD ，且GC ＝2，求点B 到平面EFG 的距离.练习(用向量法求距离):变式练习 如图,ABCD 是矩形,PD ⊥平面ABCD ,PD DC a ==,AD =,、M N 分别是、AD PB 的中点,求点A 到平面MNC 的距离.[题后感悟] (1)用向量法求点面距的方法与步骤(如本题方法一)：(2)用距离线段求点到面的距离，要作出垂线段，常常要添加辅助线，如本题中方法二；(3)用等体积转化法求点到平面的距离，要注意转化顶点后的体积较容易求，如本题中方法三．3.2.4空间向量与空间角重点：利用空间向量求线线、线面、面面所成的角．1.异面直线所成的角是否等于它们的方向向量所成的角？2.直线与平面所成角与直线的方向向量和平面法向量所成角互余吗？例1 (2011·高考北京卷改编)如图，在四棱锥P ­ABCD 中，PA ⊥平面ABCD ，底面ABCD 是菱形，AB ＝2，∠BAD ＝60°. (1)求证：BD ⊥平面PAC ；(2)若PA ＝AB ，求PB 与AC 所成角的余弦值．【名师点评】 利用向量求异面直线所成角的步骤为：(1)确定空间两条直线的方向向量；(2)求两个向量夹角的余弦值；(3)比较余弦值与0的大小,确定向量夹角的范围;(4)确定线线角与向量夹角的关系：当向量夹角为锐角时，即为两直线的夹角；当向量夹角为钝角时，两直线的夹角为向量夹角的补角．变式训练1.四棱锥P ­ABCD 中,PD ⊥平面ABCD ，PA 与平面ABCD 所成的角为60°.在四边形ABCD中,∠ADC＝∠DAB ＝90°，AB ＝4，CD ＝1，AD ＝2.(1)建立适当的坐标系，并写出点B 、P 的坐标；(2)求异面直线PA 与BC 所成的角的余弦值．求异面直线所成的角例2如图，在直三棱柱ABC －A1B1C1中，AC ⊥BC,AC ＝BC ＝CC1，M 、N 分别是A1B 、B1C1的中点．(1)求证：MN ⊥平面A1BC ；(2)求直线BC1和平面A1BC 所成角的大小．【名师点评】 利用向量法求直线与平面所成的角的基本步骤为：(1)建立空间直角坐标系；(2)求直线的方向向量；(3)求平面的法向量n ；(4)计算：设线面角为θ，则sin θ＝.变式练习正三棱柱111ABC A B C 的底面边长为a，求1AC 与侧面11ABB A 所成的角.例3.(本题满分12分)如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ∥QA ，QA ＝AB ＝12PD. 求直线与平面所成的角求二面角(1)证明：平面PQC⊥平面DCQ；(2)求二面角QBPC的余弦值．【名师点评】利用法向量求二面角的步骤为：(1)确定两平面的法向量；(2)求两法向量的夹角的余弦值；(3)确定二面角的范围；(4)确定二面角与面面角的关系：二面角范围的确定要通过图形观察，法向量一般不能体现出来．如图，PA⊥平面ABC，AC⊥BC，BC＝2，PA＝AC＝1，求二面角APBC的余弦值．综合练习已知单位正方体ABCD－A1B1C1D1，E，F分别是棱B1C1，C1D1的中点．试求：(1)AD1与EF所成角的大小；(2)AF与平面BEB1所成角的余弦值；(3)二面角C1－DB－B1的正切值．。

,a b>；θ=<>；n)所成的角sin cos,a n⑶二面角：锐二面角θ：cos cos ,m n θ=<>，其中,m n 为两个面的法向量。

活动三：合作学习、探究新知（18分钟）利用向量知识求线线角，线面角，二面角的大小。

一、异面线所成角：例1、如图所示的正方体中，已知与为四等分点，求异面直线与的夹角的余弦值？方法小结：1、异面直线a 、b 所成的角：在空间中任取一点O ，过点O 分别引/a ∥a ，/b ∥b ，则/a ，/b 所成的锐角（或直角）叫做两条异面直线所成的角。

两条异面直线所成角的范围：(0,]2π。

2、求法：①传统法：把两条异面直线中的一条放入一个平面，另一条与这个平面有交点，过这个交点在平面内作第一条的平行线，则这两条直线所成的角为两条异面直线所成的角。

然后解三角形得到。

②向量法：在直线a 上取两点A 、B ，在直线b 上取两点C 、D ，若直线a 与b 的夹角为θ，则cos |cos ,|AB CD θ=<>。

3、利用向量求异面直线所成的角的步骤为：（1）确定空间两条直线的方向向量；（2）求两个向量夹角的余弦值；（3）确定线线角与向量夹角的关系；当向量夹角为锐角时，即为两直线的夹角；当向量夹角为钝角时，两直线的夹角为向量夹角的补角。

练习：中，，现将沿着平面的法向量平移到的位置，已知BC=CA=C,取、的中点、，求B与A所成的角的余弦值。

二、直线与平面所成的角：例2：如图，在正方体ABCD-中，求与平面所成的角。

方法小结：1、直线a 与平面α所成角：斜线与平面所成的角就是斜线与它在平面内的射影所成的锐角。

直线与平面所成角的范围为：[0,]2π。

2、求法：①求斜线与平面所成的角关键是找到斜线在平面内的射影，即确定过斜线上一点向平面所作垂线的垂足，这时经常要用面面垂直来确定垂足的位置。

若垂足的位置难以确定，可考虑用三棱锥体积等量来求出斜线上一点到平面的距离。

利用法向量求二面角1. 什么是二面角在几何学中，二面角指的是两个平面的夹角，通常用来描述空间中的角度关系。

具体地说，二面角是由两个面的法向量所定义的角度，通过测量一个面对相邻面的法向量之间的夹角来计算。

2. 法向量的概念在三维空间中，平面可以通过一个法向量来定义。

法向量垂直于平面，并且指向平面的外部。

根据向量的定义，法向量具有方向和大小。

法向量的大小表示平面的倾斜程度，而法向量的方向则指示平面的朝向。

3. 利用法向量求二面角的方法要计算两个平面之间的二面角，可以利用它们的法向量。

具体的方法如下：步骤1：首先，确定两个平面的法向量。

可以通过计算平面上的三个非共线点的向量叉积来获得一个平面的法向量。

同样地，另一个平面的法向量也可以通过相同的方法来计算。

步骤2：然后，计算两个法向量之间的夹角。

夹角可以通过计算两个向量的内积的反余弦值来获得。

步骤3：最后，得到的夹角就是两个平面之间的二面角。

根据需要，可以将夹角的单位转换为度数或弧度。

4. 示例为了更好地理解利用法向量求二面角的方法，我们来看一个示例。

假设有两个平面，A和B，它们的法向量分别为n_n=(n,n,n)和n_n=(n,n,n)。

首先，计算法向量的夹角。

夹角n可以表示为n=nn+nn+nn。

然后，得到的角度n就是平面A和平面B之间的二面角。

5. 总结利用法向量可以方便地计算两个平面之间的二面角。

通过计算两个平面的法向量的夹角，可以得到二面角的值。

这个方法在计算几何学和计算机图形学中都有广泛的应用，用于描述三维空间中的角度关系。

以上就是利用法向量求二面角的说明文档，希望对你有所帮助。

如果你有任何问题或需要进一步的解释，请随时向我提问。

法向量求解二面角的平面角求二面角是高考中必考内容，学习过程中要备受关注，利用传统方法求解二面角的关键是首先知道二面角的平面角，再转化到三角形中解决，而利用法向量可以降低问题的难度，把问题转化为程序化的求解过程，本文就剖析如何利用法向量求解二面角．一、法向量求二面角步骤1、建立适当的直角坐标系，当图形中有明显互相垂直且交于一点的三条直线，可以利用这三条直线直接建系；如果没有明显交于一点的三条直线，但图形中有一定对称关系，（如正三棱柱、正四棱柱等）利用图形对称性建立空间直角坐标系解题；此外页可以利用面面垂直的性质定理，作出互相垂直且交于一点的三条直线，建立坐标系．2、求法向量：一般用待定系数法求解，一般步骤如下：（1）设出平面的法向量为n ＝（x ，y ，z ）；（2）找出（求出）平面内的两个不共线的向量的坐标),,(111c b a a =，),,(222c b a b =；（3）根据法向量的定义建立关于x 、y 、z 的方程组⎩⎨⎧=⋅=⋅00b n a n ；（4）解方程组，取其中的一个解，即得法向量£®3、利用数量积公式求角：设1n ，2n 分别是两个半平面的法向量，则由21,cos n n n n >=<求得><21,n n ，而><21,n n 的大小或其补角的大小即为二面角的大小，应注意1n ，2n 的方向。

所以二面角的大小可以通过该二面角的两个面的法向量的夹角求得，他等于两法向量的夹角或其补角．二、考题剖析例1、在四棱锥ABCD P -中，⊥PA 平面ABCD ，底面ABCD 为矩形，1(0)AB PA BC a a==>. (Ⅰ)当1a =时，求证：BD PC ⊥；(Ⅱ)若BC 边上有且只有一个点Q ，使得QD PQ ⊥，求此时二面角Q PD A --的余弦值.A BQ DCP解：(Ⅰ)当1a =时，底面ABCD 为正方形，∴BD AC ⊥ 又因为BD PA ⊥,BD ∴⊥面PAC 又PC ⊂面PAC ，BD PC ∴⊥(Ⅱ) 因为AP AD AB ,,两两垂直，分别以它们所在直线为x 轴、y 轴、z 轴建立坐标系，如图所示，令1AB =，可得BC a =，则)1,0,0(),0,,1()0,,0(),0,0,1(P a C a D B ．设m BQ =，则)0)(0,,1(a m m Q ≤≤．要使QD PQ ⊥，只要0)(1=-+-=⋅m a m QD PQ ，即210m am -+=． 由0∆=2a ⇒=，此时1m =．所以BC 边上有且只有一个点Q ，使得QD PQ ⊥时，Q 为BC 的中点，且2=a ． 设面PQD 的法向量)1,,(y x p =，则00p QD p DP ⎧⋅=⎪⎨⋅=⎪⎩即⎩⎨⎧=+-=+-0120y y x 解得)1,21,21(=p ，取平面PAD 的法向量)0,0,1(=q ，则〉〈q p .的大小与二面角Q PD A --的大小相等，所以66.cos ==〉〈q p q p ， 因此二面角Q PD A --的余弦值为66．点评：一般情况下求法向量用待定系数法.由于法向量没规定长度，仅规定了方向，所以有一个自由度，可把n 的某个坐标设为1，再求另两个坐标.求解法向量一般借助方程思想，几何问题代数化，求得法向量再结合向量数量积公式求得二面角．例2、在如图所示的四面体ABCD 中，AB 、BC 、CD 两两互相垂直，且BC = CD = 1．求二面角C －AB －D 的大小；分析：由于本题中没有垂直关系，需要寻找（或作出三线垂直的直线）．解：根据已知容易证明BCD AB 平面⊥，设以过B 点且∥CD 的向量为x 轴，BC BA 、为y 轴和z 轴建立如图所示的空间直角坐标系，设AB = a ，则A (0，0，a )，C (0，1，0)，D (1，1，0)，BD = (1，1，0)，BA = (0，0，a )平面ABC 的法向量CD = (1，0，0)．设平面ABD 的一个法向量为n = (x ，y ，z )，则0000BD x y az BA ⎧⋅=+=⎧⎪⇒⎨⎨=⋅=⎩⎪⎩n n ，取n = (1，－1，0)．∴cos ||||CD CD CD ⋅<>==⋅n n n ，∴二面角C －AB －D 的大小为45°点评：解决本题关键是建立合适的直角坐标系，求得点的坐标，从而求得法向量。

第三课时用向量方法求空间中的角课时演练·促提升A组1.已知A(0,1,1),B(2,-1,0),C(3,5,7),D(1,2,4),则直线AB和直线CD所成角的余弦值为()A. B.-C. D.-解析:=(2,-2,-1),=(-2,-3,-3),而cos =,故直线AB和CD所成角的余弦值为.答案:A2.若直线l的方向向量与平面α的法向量的夹角等于120°,则直线l与平面α所成的角等于()A.120°B.60°C.30°D.以上均错解析:∵l的方向向量与平面α的法向量的夹角为120°,∴它们所在直线的夹角为60°.则直线l与平面α所成的角为90°-60°=30°.答案:C3.若二面角α-l-β的大小为120°,那么平面α与平面β的法向量的夹角为()A.120°B.60°C.120°或60°D.30°或150°解析:二面角为120°时,其法向量的夹角可能是60°,也可能是120°.答案:C4.在正方体ABCD-A1B1C1D1中,M是AB的中点,则sin<>的值为()A. B. C. D.解析:如图,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.设正方体的棱长为1,则D(0,0,0),B1(1,1,1),C(0,1,0),M,∴=(1,1,1),,∴cos<>==,∴sin<>=.答案:B5.如图,过边长为1的正方形ABCD的顶点A作线段EA⊥平面ABCD,若EA=1,则平面ADE与平面BCE所成的二面角的大小是()A.120°B.45°C.135°D.60°解析:以A为原点,分别以AB,AD,AE所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则E(0,0,1),B(1,0,0),C(1,1,0),则=(1,0,-1),=(1,1,-1).设平面BCE的法向量为n=(x,y,z).则有可取n=(1,0,1),又平面EAD的法向量为=(1,0,0),所以cos n, =,故平面ADE与平面BCE所成的二面角为45°.答案:B6.在正四棱锥P-ABCD中,高为1,底面边长为2,E为BC的中点,则异面直线PE与DB所成的角为. 解析:建立空间直角坐标系如图,则B(1,1,0),D(-1,-1,0),E(0,1,0),P(0,0,1), 故=(2,2,0),=(0,1,-1).从而cos<>=,即<>=.于是PE与DB所成的角为.答案:7.若空间直线l的方向向量为t,平面α的法向量为n,t与n的夹角θ>,则l与α所成角为. 解析:如图可知,l与α所成角为θ-.答案:θ-8.如图,已知ABC-A1B1C1是直三棱柱,∠ACB=90°,点D1,F1分别是A1B1,A1C1的中点,BC=CA=CC1,求BD1与AF1所成角的余弦值.解:如图,以C为原点,CA,CB,CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系, 设CB=CA=CC1=1,则A(1,0,0),B(0,1,0),D1,F1,则.故||=,||=,则cos<>=.于是BD1与AF1所成角的余弦值为.9.在正方体ABCD-A1B1C1D1中,E,F分别为AA1,AB的中点,求EF和平面ACC1A1夹角的大小.解:建立如图的空间直角坐标系,设正方体棱长为2,则由E,F分别是AA1,AB的中点,得E(2,0,1),F(2,1,0).过F作FG⊥AC于G,则由正方体性质知FG⊥平面ACC1A1.连接EG,则的夹角即为所求,又因为F是AB的中点,所以AG=AC,所以G=(0,1,-1).cos<>=.∴<>=,即EF与平面ACC1A1的夹角为.10.在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.(1)求证:BD⊥平面AED;(2)求二面角F-BD-C的余弦值.(1)证明:∵四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,∴∠ADC=∠BCD=120°.又∵CB=CD,∴∠CDB=30°.∴∠ADB=90°,即AD⊥BD.又∵AE⊥BD,且AE∩AD=A,AE⊂平面AED,AD⊂平面AED,∴BD⊥平面AED.(2)解:由(1)知AD⊥BD,∴AC⊥BC.又FC⊥平面ABCD,因此CA,CB,CF两两垂直.以C为坐标原点,分别以CA,CB,CF所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.不妨设CB=1,则C(0,0,0),B(0,1,0),D,F(0,0,1),因此=(0,-1,1).设平面BDF的一个法向量为m=(x,y,z),则m·=0,m·=0,即x-y=0,-y+z=0,所以x=y=z.令z=1,得m=(,1,1).由于=(0,0,1)是平面BDC的一个法向量,则cos<m,>=,故二面角F-BD-C的余弦值为.B组1.已知在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.则直线AE与平面A1ED1所成角的大小为()A.60°B.90°C.45°D.以上都不正确解析:以点D为原点,分别以DA,DC,DD1所在直线为x轴,y轴,z轴,建立空间直角坐标系,如图.由题意知,A1(1,0,2),E(1,1,1),D1(0,0,2),A(1,0,0),所以=(0,1,-1),=(1,1,-1),=(0,-1,-1).设平面A1ED1的一个法向量为n=(x,y,z),则令z=1,得y=1,x=0,所以n=(0,1,1),cos<n,>==-1.所以<n,>=180°.所以直线AE与平面A1ED1所成的角为90°.答案:B2.在空间中,已知平面α过点(3,0,0)和(0,4,0)及z轴上一点(0,0,a)(a>0),如果平面α与平面xOy的夹角为45°,则a=.解析:平面xOy的法向量为n=(0,0,1),设平面α的法向量为u=(x,y,z),则则3x=4y=az,取z=1,则u=,而cos<n,u>=.又a>0,故a=.答案:3.在四面体ABCD中,O是BD的中点,|CA|=|CB|=|CD|=|BD|=2,|AB|=|AD|=,则异面直线AB与CD所成的角的余弦值是.解析:以O为原点,建立如图所示的空间直角坐标系,则点B(1,0,0),D(-1,0,0),C(0,,0),A(0,0,1),=(-1,0,1),=(-1,-,0).所以cos<>=.故异面直线AB与CD所成的角的余弦值为.答案:4.在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,E是PD的中点,求二面角E-AC-D的大小.解:如图,以A为原点,分别以AC,AB,AP所在直线为x轴、y轴、z轴建立空间直角坐标系.设PA=AB=a,AC=b.连接BD与AC交于O,取AD中点F,连接OE,OF,EF,则C(b,0,0),B(0,a,0),.∴D(b,-a,0),P(0,0,a).∴E,O=(b,0,0),∵=0,∴=0.∴.∴∠EOF为二面角E-AC-D的平面角.cos =.∴二面角E-AC-D的大小为45°.5.如图,已知点P在正方体ABCD-A'B'C'D'的对角线BD'上,∠PDA=60°.(1)求DP与CC'所成角的大小;(2)求DP与平面AA'D'D所成角的大小.解:如图,以D为原点,DA为单位长度建立空间直角坐标系Dxyz.则=(1,0,0),=(0,0,1).连接BD,B'D'.在平面BB'D'D中,延长DP交B'D'于点H.设=(m,m,1)(m>0),由已知<>=60°,由=||||cos<>,可得2m=,解得m=,所以.(1)因为cos<>=,所以<>=45°,即DP与CC'所成的角为45°.(2)平面AA'D'D的一个法向量是=(0,1,0).因为cos<>=,所以<>=60°.故DP与平面AA'D'D所成的角为30°.6.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.(1)求证:PC⊥AD;(2)求二面角A-PC-D的正弦值;(3)若E为棱PA上的点,且异面直线BE与CD所成的角为30°,求AE的长.解:如图,以点A为原点,AD,AC,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,由题意得A(0,0,0),D(2,0,0),C(0,1,0),B,P(0,0,2).(1)证明:易得=(0,1,-2),=(2,0,0),于是=0,所以PC⊥AD.(2)=(0,1,-2),=(2,-1,0).设平面PCD的法向量n=(x,y,z),则不妨令z=1,可得n=(1,2,1).可取平面PAC的法向量m=(1,0,0).于是cos<m,n>=,从而sin<m,n>=.所以二面角A-PC-D的正弦值为.(3)设点E的坐标为(0,0,h),其中h∈[0,2].由此得=(2,-1,0),故cos<>==.所以=cos 30°=,解得h=,即AE的长为.。