正弦电压与电流
- 格式:doc
- 大小:131.50 KB
- 文档页数:2


在正弦交流电路中,电压与电流的超前滞后关系
在正弦交流电路中,电压与电流的相位关系可以通过超前和滞后这两个概念来描述。
1. 电压与电流的相位差:当电压和电流都是正弦波时,它们之间存在一定的相位差。
相位差可以是0度、90度、180度等,具体取决于电路元件的性
质和连接方式。
2. 超前与滞后的概念:在相位上,如果电压相对于电流是超前的,这意味着电压的峰值比电流的峰值早到达。
相反,如果电压相对于电流是滞后的,则电压的峰值比电流的峰值晚到达。
3. 应用场景:超前和滞后的相位关系取决于电路中元件的种类和连接方式。
例如,纯电阻性负载时,电压和电流同相位;纯电感性负载时,电流滞后于电压90度;纯电容性负载时,电流超前于电压90度。
这些相位关系在分
析交流电路时非常重要,因为它们决定了电路的工作特性和元件之间的相互影响。
综上所述,电压与电流的超前和滞后关系取决于电路的元件性质和连接方式,分析这些关系有助于深入理解交流电路的工作原理。


电工技术与电子技术—常见问题
模块五 正弦交流电路(1)
1.正弦交流电路中,有效值和最大值以及峰峰值之间有什么关系?有效值为220V 的交流电压最大值是不是380V ?
在正弦交流电路中,最大值是有效值的倍,峰峰值为最大值的2倍,也就是说
峰峰值是有效值的2倍。
有效值为220V 的交流电压其最大值为V ,也即311V 。
2. 正弦量采用相量表示时,正弦量的角频率为什么没有加以体现?
由于在采用相量表示法进行计算时,都是同频率的正弦量,所以在应用相量来表示正弦量以及画相量图的时候都是可以不用考虑正弦量的频率的。
3. 在计算交流电路时,到底采用有效值相量还是最大值相量?
两者都可以,最大值相量的模是最大值,而有效值相量的模是有效值,在计算时可以根据实际需要,如需要计算电压、电流的最大值时,可以用最大值相量,一般计算时采用有效值相量居多。
4. 正弦量的表示方法有哪些,为什么在电路计算过程中要采用相量分析法?
正弦量可以采用三角的形式以及波形图的方式来进行表示,也可以采用相量的方法来表示,由于在电路计算过程中会遇到很多正弦量的加减运算,采用相量表示法更容易进行计算,因此在正弦交流电路的计算过程中,都采用相量来表示正弦量。
5. 一个正弦量为30)V =+ᄚu t ,另外一个正弦量为
60)V =+ᄚu t ,这两个正弦量之间有没有相位差一说?
没有,相位差指的是两个同频率正弦量之间的相位之差,对于不同频率的正弦量两者比较相位差没有任何意义,因此两个不同频率的正弦量之间没有相位差一说。



纯电感元件在正弦交流电路中的电压与电流关系
在正弦交流电路中,纯电感元件的电压与电流之间存在一定的关系。
根据电感元件的特性,其电压与电流的关系可以通过以下公式表示:
V = jωLI
其中,V表示电感元件的电压,I表示电感元件的电流,L表示电感元件的电感值,ω表示电路中的角频率。
j是虚数单位,满足j² = -1。
这个公式表明,电压与电流之间存在90度的相位差,且电压与电流之间的关系是线性的,也就是电压与电流成正比。
当电流通过电感元件时,会产生一个由电感元件本身决定的感应电动势,从而引起电压的变化。
需要注意的是,电感元件在交流电路中会引入阻抗,即纯电感元件的阻抗Z可以表示为:
Z = jωL
因此,在交流电路中,纯电感元件的电压和电流之间不仅存在幅值比例关系,还存在相位差。
这个相位差由纯电感元件的阻抗决定,通常为正90度。



正弦交流电压与电流随时间按正弦规律变化的电压和电流分别称为正弦电压和正弦电流,一般可用正弦时间函数式表示如下( 此处以电压为例)(1 )同—正弦电压也可用余弦函数表示为式中本文中,一般均采用前—种表示法。
式(1) 中,为正弦电压的幅值即极大值;为正弦函数的辐角〔argument) ,称为瞬时相角,简称相角(phase) 或相(phase), 它是随时间而变化的;为t=0 时的瞬时相角,称为初相角.简称初相(initial phase) 。
瞬时相角决定着正弦函数随时间t 变化的进程,而初相则表示在初始时刻正弦函数的辐角。
设正弦电压随时间变化的周期(period) 为T, 频率为,则式(6—1—1) 中,当时间t 从零增加至T 时,对应的辐角应增加2 π。
换言之,故(2 )表示每经过单位时间,瞬时相角所增加的角度,称为角频率,在国际单位制中,角频率的单位为弧度每秒( 符号为rad/s) 。
它与正弦量的频率成正比。
任一正弦量,其幅值、初相及角频率( 或频率) 确定以后,该正弦量就被完全地确定下来。
故幅值、初相及角频率称为正弦量的三要素。
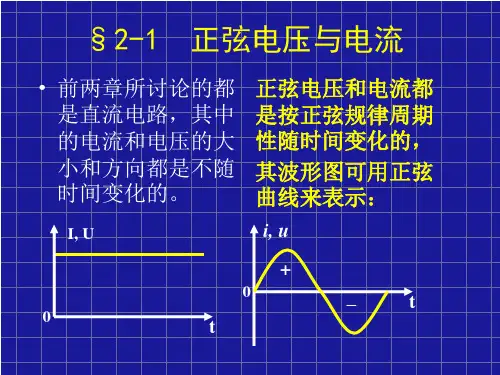
图1 正弦交流电压波形正弦电压和电流也可用波形图表示。
图6—1—1 绘出了两个频率及幅值相同而初相不同的正弦电压和的波形。
图中的横坐标分别以时间t 及角度t 为自变量标出。
由图可知,两个正弦被之间存在着相角差(phase difference) ,并且的相角超前于的相角,或者说的相角滞后于的相角。
一般设两个同频率的正弦量和分别为它们之间的相位差即等于二者的初相之差。
是超前于的相角;反之,则是超前于的相角。
如果,,即则称与同相(in phase) ;反之,如果,则称与反相(opposite phase) 。
在正弦电流电路的分析、汁算和实际应用中,通常采用有效值表示正弦电压、电流的大小( 而不是用幅值) 。
下面以电流为例介绍有效值的概念。
首先研究周期电流的有效值。
对于任何一个随时间按一定周期规律变化的电流,在实际应用中,常常没有必要表示出它在每一瞬时的值,而希望定义一个能够反映周期电流平均作功能力的量,即所谓的有效值。
1. 正弦电压和电流的一般表示形式随时间按正弦规律变化的电压和电流称为正弦电压和正弦电流,它们都属正弦波。
既可用时间的sin 函数表示,也可用时间的余弦函数表示(本书采用cos 函数表示,但仍称为正弦波),具体形式如下)cos()(u m t U t u θω+= (1))cos()(i m t I t i θω+= (2)2.正弦电压和电流的三要素1)1)振幅:(1)和(2)式中的m U 和m I 称为它们的振幅,是电压和电流的最大值。
2)2)ω称为角频率,表示了单位时间内变化的弧度数,单位为:弧度/秒(rad/s )。
余周期频率间的关系如下f T ππω22==3)3)初相位(u θ和i θ):θω+t 称为相位角,简称相位,是时间的函数。
不同的时间对应着不同的相位值,不同的相位对应着不同的电压和电流的瞬时值。
因此,相位表示了正弦波变化的进程。
当0=t 时的相位值,即θ称为初相位简称初相,反映了正弦波初始值的大小。
3.同频率正弦量(电压和电流)间的关系对两个同频率的正弦量而言,它们之间的区别在于振幅和初相。
但在研究它们之间的相互关系时,只关心的是它们的初相及其差值,初相不同,表明它们随时间变化的“步调”不)cos()(111θω+=t U t u m , )cos()(222θω+=t U t u m这两个同频率的正弦波的初相的差值反映了它们“步调”不一致的情况。
初相之差,也即相位角之差,称为相位差,记为12φ,即2112-θθφ=表示了1u 的相位超前于2u ,或2u 的相位滞后于1u 的角度。
三种特殊情况:1)1)若012=φ,则两个正弦波同相位,简称同相,它们同时到达最大值,变化的“步调”一致;2)2)若212πφ±=,则称两个正弦波相位正交;3)3)若πφ=12,则称两个正弦波的相位相反,简称反相。
[例] 设有两个同频率的正弦电流A )43cos()(1πω+=t I t i m ,A )2-cos()(2πωt I t i m = 问哪一电流滞后?滞后的角度是多少? 解:根据2112-θθφ=得πππθθφ45)2(--43-2112===由于012>φ,表明2i 滞后于1i ,滞后的角度为π45,如图所示。
正弦电压与电流
大小、方向随时间变化的电压、电流称为交流电,
按正弦规律变化的电压、电流称为正弦交流电(简称正弦量)。
一、正弦量的三要素
如图1所示,正弦电量的表达式为:
式中的称为正弦交流电的三要素。
1、振幅:正弦交流电变化过程中最大瞬时值的绝对值。
2、角频率:单位时间内交流电所经历的电角度(反映交流电变化快慢的物理量)。
交流电周期为 T,(交流电变化一周所需要的时间),
频率为f(交流电每秒所变化的周数),则:f =1/ T
角频率为:
3、初相位:
相位(相位角):——交流电某时刻所处的位置 ( 或者电角
度 ) ,
反映正弦量变化的进程。
初相位: t=0 时的相位,初相不大于180°。
相位差:两个同频率的正弦量在任一瞬间的相位之差。
相位的超前与滞后:
二、正弦量的有效值
我们平时常说的220V及测量的电流的读数等,均指有效值。
定义:若一个交流电流i和一个直流电流I在相同的时间内通过同一电阻
产生的热量相等. 则我们称I为i的有效值。
根据定义可以推导出:
同理可得电压的有效值:
三、正弦量的相量表示
用复数表示的正弦量 , 称为相量。
相量的模对应正弦量的有效值;相量的复角对应正弦量的初相角。
<注>:角频率可不参予讨论(因为同频率的正弦量运算的结果所得到的频率不变)。
相量值等于有效值和单位极式的乘积,例:
说明:(1)复数只是一个运算工具 , 它在运算上与正弦量具有等效性 , 但它们并不相等
(2)同频率的正弦量所代表的相量可以画在同一复平面上 , 这样的图称为
相量图。