【高中数学】第2讲 命题及其关系、充分条件与必要条件

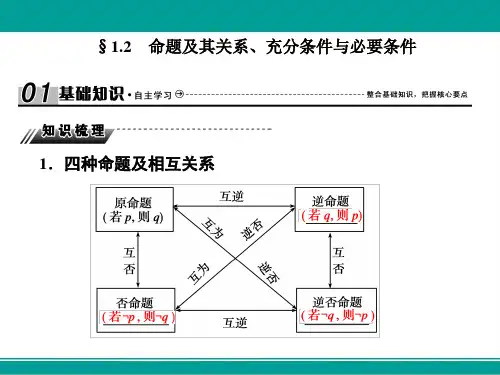
考点二命题及其关系、充分条件与必要条件知识梳理1．命题的概念可以判断真假、用文字或符号表述的语句，叫作命题．其中判断为真的语句叫真命题，判断为假的语句叫假命题．2．四种命题及相互关系(1) 四种命题命题表述形式原命题若p，则q逆命题若q，则p否命题若非p，则非q逆否命题若非q，则非p(2) 四种命题间的逆否关系3．四种命题的真假关系(1)两个命题互为逆否命题，它们有相同的真假性；(2)两个命题互为逆命题或互为否命题，它们的真假性没有关系．4．充分条件与必要条件(1)如果p⇒q，则p是q的充分条件，q是p的必要条件；(2)如果p⇒q，q⇒p，则p是q的充要条件．(3) 如果p q，q p，那么称p是q的充分不必要条件．(4) 如果q p，p q，那么称p是q的必要不充分条件．(5) 如果p q，且q p，那么称p是q的既不充分也不必要条件．典例剖析题型一四种命题及其相互关系例1命题“若一个数是负数，则它的平方是正数”的逆命题是()A．“若一个数是负数，则它的平方不是正数”B．“若一个数的平方是正数，则它是负数”C．“若一个数不是负数，则它的平方不是正数”D．“若一个数的平方不是正数，则它不是负数”答案 B解析将原命题的条件与结论互换即得逆命题，故原命题的逆命题为“若一个数的平方是正数，则它是负数”．变式训练命题“若x，y都是偶数，则x＋y也是偶数”的逆否命题是()A．若x＋y是偶数，则x与y不都是偶数B．若x＋y是偶数，则x与y都不是偶数C．若x＋y不是偶数，则x与y不都是偶数D．若x＋y不是偶数，则x与y都不是偶数答案 C解析由于“x，y都是偶数”的否定表达是“x，y不都是偶数”，“x＋y是偶数”的否定表达是“x ＋y不是偶数”，故原命题的逆否命题为“若x＋y不是偶数，则x，y不都是偶数”，故选C.解题要点 1.写一个命题的其他三种命题时，需注意：①对于不是“若p，则q”形式的命题，需先改写；②若命题有大前提，写其他三种命题时需保留大前提．2.一些常见词语的否定例2有下列几个命题：①“若a＞b，则a2＞b2”的否命题；②“若x＋y＝0，则x，y互为相反数”的逆命题；③“若x2＜4，则－2＜x＜2”的逆否命题．其中真命题的序号是________．答案②③解析①原命题的否命题为“若a≤b，则a2≤b2”，错误．②原命题的逆命题为：“若x，y互为相反数，则x＋y＝0”，正确．③原命题的逆否命题为“若x≥2或x≤－2，则x2≥4”，正确．变式训练下列有关命题的说法正确的是________．(填序号)①命题“若x2＝1，则x＝1”的否命题为“若x2＝1，则x≠1”；②若一个命题是真命题，则其逆命题也是真命题；③命题“存在x∈R，使得x2＋x＋1<0”的否定是“对任意x∈R，均有x2＋x＋1<0”；④命题“若x＝y，则sin x＝sin y”的逆否命题为真命题．答案 ④解析 命题“若x 2＝1，则x ＝1”的否命题为“若x 2≠1，则x ≠1”，所以①不正确；原命题与逆命题不等价，所以②不正确；命题“存在x ∈R ，使得x 2＋x ＋1<0”的否定是“对任意x ∈R ，均有x 2＋x ＋1≥0”，所以③不正确；命题“若x ＝y ，则sin x ＝sin y ”是真命题，所以逆否命题为真命题，④正确．解题要点 1.判断一个命题为真命题，要给出推理证明；判断一个命题是假命题，只需举出反例．2.根据“原命题与逆否命题是等价的，逆命题与否命题也是等价的”这一性质，当一个命题直接判断不易进行时，可转化为判断其等价命题的真假．题型二 充分条件与必要条件例3 已知p ：“a ，b ，c 成等比数列”，q ：“b ＝ac ”，那么p 是q 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案 D解析 若a ，b ，c 成等比数列，则有b 2＝ac ，所以b ＝±ac ，所以充分性不成立．当a ＝b ＝c ＝0时，b ＝ac 成立，但此时a ，b ，c 不成等比数列，所以必要性不成立，所以p 是q 的既不充分也不必要条件．变式训练 在△ABC 中，角A ，B ，C 所对应的边分别为a ，b ，c ，则“a ≤b ”是“sin A ≤sin B ”的( )A ．充分必要条件B ．充分非必要条件C ．必要非充分条件D ．非充分非必要条件答案 A解析 由正弦定理，知a ≤b ⇔2R sin A ≤2R sin B (R 为△ABC 外接圆的半径)⇔sin A ≤sinB ． 例4 设函数f (x )＝log 2x ，则“a ＞b ”是“f (a )＞f (b )”的________(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)条件．答案 必要不充分解析 因为f (x )＝log 2x 在区间(0，＋∞)上是增函数，所以当a >b >0时，f (a )>f (b )；反之，当f (a )>f (b )时，a >b .故“a ＞b ”是“f (a )＞f (b )”的必要不充分条件．变式训练 设x ∈R ，则“x >1”是“220x x +->”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 答案 A解析 由不等式220x x +->得(2)(1)0x x +->，即2x <-或1x >，所以由1x >可以得到不等式220x x +->成立，故充分性成立；但由220x x +->不一定得到1x >，所以必要性不成立，即“x >1”是“220x x +->”的充分而不必要条件．解题要点 1．充要条件问题应首先弄清问题中条件是什么，结论是什么，再进一步判断条件与结论的关系，解题过程分为三步：①确定条件是什么，结论是什么；②尝试从条件推结论，从结论推条件；③确定条件和结论是什么关系．2．充要条件的三种判断方法(1) 定义法：根据p q ，q p 进行判断； (2) 集合法：根据p 、q 成立的对象的集合之间的包含关系进行判断；(3) 等价转化法：根据一个命题与其逆否命题的等价性，把判断的命题转化为其逆否命题进行判断．当堂练习1. 设p ：1<x <2，q ：2x >1，则p 是q 成立的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件2．设,a b ∈R , 则 “2()0a b a -<”是“a b <”的 ( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件3．已知m ，n 是两条不同直线，α，β是两个不同平面，则下列命题正确的是( )A ．若α，β垂直于同一平面，则α与β平行B ．若m ，n 平行于同一平面，则m 与n 平行C ．若α，β不平行，则在α内不存在与β平行的直线D ．若m ，n 不平行，则m 与n 不可能垂直于同一平面4．已知i 是虚数单位，a ，b ∈R ，得“a ＝b ＝1”是“(a ＋b i)2＝2i ”的 条件．5.U 为全集,A ,B 是集合,则“存在集合C 使得A ⊆C ，B ⊆∁U C ”是“A ∩B ＝∅” 条件．课后作业一、 选择题1．下列语句中命题的个数是( )①2<1；②x <1；③若x <2，则x <1；④函数f (x )＝x 2是R 上的偶函数.A.0B.1C.2D.32．“x ＝1”是“x 2－2x ＋1＝0”的( )A ．充要条件B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件3．“1<x <2”是“x <2”成立的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．设p ：x <3，q ：－1<x <3，则p 是q 成立的( )A ．充分必要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件5．下列结论错误的是( )A ．命题“若x 2－3x －4＝0，则x ＝4”的逆否命题为“若x ≠4，则x 2－3x －4≠0”B ．“x ＝4”是“x 2－3x －4＝0”的充分条件C ．命题“若m >0，则方程x 2＋x －m ＝0有实根”的逆命题为真命题D ．命题“若m 2＋n 2＝0，则m ＝0且n ＝0”的否命题是“若m 2＋n 2≠0，则m ≠0或n ≠0”6．若m ∈R, 命题“若m >0，则方程x 2＋x －m ＝0有实根”的逆否命题是( )A ．若方程x 2＋x －m ＝0有实根，则m ＞0B ．若方程x 2＋x －m ＝0有实根，则m ≤0C ．若方程x 2＋x －m ＝0没有实根，则m ＞0D ．若方程x 2＋x －m ＝0没有实根，则m ≤07．已知命题p ：若x ＝－1，则向量a ＝(1，x )与b ＝(x ＋2，x )共线，则在命题p 的原命题、逆命题、否命题、逆否命题中，真命题的个数为( )A ．0B ．2C ．3D ．48．设α，β是两个不同的平面，m 是直线且m ⊂α.“m ∥β”是“α∥β”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件二、填空题9．x ≠3或y ≠5是x ＋y ≠8的____________条件．(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)10．“若a ≤b ，则ac 2≤bc 2”，则命题的原命题、逆命题、否命题和逆否命题中真命题的个数是________．11．(1)“x >y >0”是“1x <1y”的________条件． (2) 设a ，b ∈R ，则“a ＞b ”是“a |a |＞b |b |”的________条件．12．下列命题：①“若k ＞0，则方程x 2＋2x ＋k ＝0有实根”的否命题；②“若1a ＞1b，则a ＜b ”的逆命题；③“梯形不是平行四边形”的逆否命题，其中是假命题的是________.13．“m <14”是“一元二次方程x 2＋x ＋m ＝0有实数解”的____________条件．当堂练习答案1. 答案 A解析 当1<x <2时，2<2x <4，∴p ⇒q ；但由2x >1，得x >0，∴q p ，故选A.2答案 A解析 由(a －b )a 2<0⇒a ≠0且a <b ，∴充分性成立；由a <b ⇒a －b <0，当0＝a <b 时 (a －b )·a 2<0，必要性不成立；故选A.3．答案 D解析 对于A ，α，β垂直于同一平面，α，β关系不确定，A 错；对于B ，m ，n 平行于同一平面，m ，n 关系不确定，可平行、相交、异面，故B 错；对于C ，α，β不平行，但α内能找出平行于β的直线，如α中平行于α，β交线的直线平行于β，故C 错；对于D ，若假设m ，n 垂直于同一平面，则m ∥n ，其逆否命题即为D 选项，故D 正确．4．答案 充分不必要条件解析 当a ＝b ＝1时，(a ＋b i)2＝(1＋i)2＝2i ；当(a ＋b i)2＝2i 时，得⎩⎪⎨⎪⎧a 2－b 2＝0，ab ＝1， 解得a ＝b ＝1或a ＝b ＝－1，所以“a ＝b ＝1”是“(a ＋b i)2＝2i ”的充分不必要条件．5.答案 充要条件解析 若存在集合C 使得A ⊆C ，B ⊆∁U C ，则可以推出A ∩B ＝∅；若A ∩B ＝∅，由Venn 图(如图)可知，存在A ＝C ，同时满足A ⊆C ，B ⊆∁U C .故“存在集合C 使得A ⊆C ，B ⊆∁U C ”是“A ∩B ＝∅”的充要条件．课后作业答案二、 选择题1．答案 D2．答案 A解析 解x 2－2x ＋1＝0得x ＝1，所以“x ＝1”是“x 2－2x ＋1＝0”的充要条件．3．答案 A4．答案 C解析 ∵x <3－1<x <3，但－1<x <3⇒x <3，∴p 是q 的必要不充分条件，故选C.5．答案 C解析 C 项命题的逆命题为“若方程x 2＋x －m ＝0有实根，则m >0”．若方程有实根，则Δ＝1＋4m ≥0，即m ≥－14，不能推出m >0.所以不是真命题，故选C. 6．答案 D解析 原命题为“若p ，则q ”，则其逆否命题为“若q ，则p ”．∴所求命题为“若方程x 2＋x －m ＝0没有实根，则m ≤0”．7．答案 B解析 向量a ，b 共线⇔x －x (x ＋2)＝0⇔x ＝0或x ＝－1，∴命题p 为真，其逆命题为假，故在命题p 的原命题、逆命题、否命题、逆否命题中，真命题的个数为2.8．答案 B解析 m ⊂α，m ∥βα∥β，但m ⊂α，α∥β⇒m ∥β，∴m ∥β是α∥β的必要而不充分条件． 二、填空题9．答案 必要不充分解析 设p ：x ＝3且y ＝5，q ：x ＋y ＝8，显然p 是q 的充分不必要条件，∴p 是q 的必要不充分条件，即x ≠3或y ≠5是x ＋y ≠8的必要不充分条件．10．答案 2解析 其中原命题和逆否命题为真命题，逆命题和否命题为假命题．11．答案 (1)充分不必要 (2)充要解析 (1)1x <1y⇒xy ·(y －x )<0， 即x >y >0或y <x <0或x <0<y .所以x >y >0 ⇒1x <1y ，但反过来1x <1y， 所以是充分不必要条件．(2) 构造函数f (x )＝x |x |，则f (x )在定义域R 上为奇函数．因为f (x )＝⎩⎪⎨⎪⎧x 2，x ≥0，－x 2，x ＜0，所以函数f (x )在R 上单调递增，所以a ＞b ⇔f (a )＞f (b )⇔a |a |＞b |b |. 所以是充要条件．12．答案 ①②解析 对于①其否命题为“若k ≤0，则方程x 2＋2x ＋k ＝0无实根”，为假命题；②的逆命题为“若a ＜b ，则1a ＞1b”，为假命题；③中原命题为真命题，故其逆否命题也为真命题. 13．答案 充分不必要解析 x 2＋x ＋m ＝0有实数解等价于Δ＝1－4m ≥0，即m ≤14，因为m <14⇒m ≤14，反之不成立． 故“m <14”是“一元二次方程x 2＋x ＋m ＝0有实数解”的充分不必要条件．。

第2讲命题及其关系、充分条件与必要条件1.命题(1)命题的概念:数学中把用语言、符号或式子表达的,能够判断的陈述句叫作命题.其中的语句叫作真命题, 的语句叫作假命题.(2)四种命题及其相互关系图1-2-1特别提醒:若两个命题互为逆否命题,则它们有相同的真假性.2.充分条件、必要条件与充要条件(1)如果p⇒q,则p是q的条件.(2)如果q⇒p,则p是q的条件.(3)如果既有p⇒q,又有q⇒p,记作p⇔q,则p是q的条件.常用结论1.充要条件的两个结论:(1)若p是q的充分不必要条件,q是r的充分不必要条件,则p是r的充分不必要条件;(2)若p是q的充分不必要条件,则q是p的充分不必要条件.2.题组一常识题1.[教材改编]对于下列语句:①垂直于同一直线的两条直线必平行吗?②作△ABC∽△A'B'C'.③x2+2x-3<0.④四边形的内角和是360°.其中是命题的是.(填序号)2.[教材改编]有下面4个命题:①集合N中最小的数是1;②若-a不属于N,则a 属于N;③若a∈N,b∈N,则a+b的最小值为2;④x2+1=2x的解集可表示为{1,1}.其中真命题的个数为.3.[教材改编]命题“若整数a不能被2整除,则a是奇数”的逆否命题是.4.[教材改编]“点P(x,y)在第一象限”是“x+y>1”的条件. 题组二常错题◆索引:命题的条件与结论不明确;含有大前提的命题的否命题易出现否定大前提的情况;真、假命题的推理考虑不全面;对充分必要条件判断错误.5.命题“若a2+b2=0,a,b∈R,则a=b=0”的逆否命题是.6.已知命题“对任意a,b∈R,若ab>0,则a>0”,则它的否命题是.7.若命题“ax2-2ax-3>0不成立”是真命题,则实数a的取值范围是.8.条件p:x>a,条件q:x≥2.①若p是q的充分不必要条件,则a的取值范围是;②若p是q的必要不充分条件,则a的取值范围是.9.已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q 的条件.探究点一四种命题及其相互关系例1 (1)对于命题“单调函数不是周期函数”,下列说法正确的是( )A.逆命题为“周期函数不是单调函数”B.否命题为“单调函数是周期函数”C.逆否命题为“周期函数是单调函数”D.以上都不正确(2)给出以下四个命题:①“若x+y=0,则x,y互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若q≤-1,则x2+x+q=0有实根”的逆否命题;④若ab是正整数,则a,b都是正整数.其中为真命题的是.(写出所有真命题的序号)[总结反思](1)求一个命题的其他三种命题时,需注意:①对于不是“若p,则q”形式的命题,需先改写为“若p,则q”的形式;②若命题有大前提,写其他三种命题时需保留大前提.(2)判断一个命题为真命题,要给出推理证明;判断一个命题为假命题,只需举出反例.(3)当不易直接判断一个命题的真假时,根据互为逆否命题的两个命题同真同假,可转化为判断其等价命题的真假.变式题(1)已知命题p:正数a的平方不等于0,命题q:若a不是正数,则它的平方等于0,则q是p的( )A.逆命题B.否命题C.逆否命题D.否定(2)以下关于命题的说法正确的是.(填写所有正确说法的序号)①“若log2(a+1)>1,则函数f(x)=logax(a>0,a≠1)在其定义域内是增函数”是真命题;②命题“若a≠0,则a(b+1)≠0”的否命题是“若a=0,则a(b+1)=0”;③命题“若x,y都是偶数,则(x+1)(y+1)是偶数”的逆命题为真命题;④命题“若a∈M,则b∉M”与命题“若b∈M,则a∉M”等价.探究点二充分、必要条件的判定例2 (1)[2018·北京卷]设a,b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件(2)“函数f(x)=a+ln x(x≥e)存在零点”是“a<-1”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[总结反思]充分条件、必要条件的判定方法有定义法、集合法和等价转化法.三种不同的方法适用于不同的类型:定义法适用于定义、定理的判断问题;集合法多适用于命题中涉及参数的取值范围的推断问题;等价转化法适用于条件和结论中带有否定性词语的命题.变式题(1)[2018·深圳一模]已知数列{a n}是等比数列,则“a2>a1”是“数列{a n}为递增数列”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件(2)“α=”是“sin 2α-cos 2α=1”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件探究点三充分、必要条件的应用例3 方程ax2+2x+1=0至少有一个负实根的充要条件是( )A.0<a≤1B.a<1C.a≤1D.0<a≤1或a<0[总结反思]充分条件、必要条件的应用一般表现在参数问题的求解上,解题时通常把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.解题过程中要注意检验区间端点值.变式题(1)下面四个条件中,使a>b成立的必要而不充分条件是( )A.a-1>bB.a+1>bC.|a|>|b|D.a3>b3(2)[2018·衡阳4月调研]已知p:实数m满足m2+12a2<7am(a>0),q:方程-+-=1表示焦点在y轴上的椭圆,且p是q的充分不必要条件,则a的取值范围为.第2讲命题及其关系、充分条件与必要条件考试说明 1.理解命题的概念;2.了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系;3.理解必要条件、充分条件与充要条件的含义.【课前双基巩固】知识聚焦1.真假判断为真判断为假2.(1)充分(2)必要(3)充要对点演练1.④[解析]①是疑问句,不是命题;②是祈使句,不是命题;③不能判断真假,不是命题;④是命题.2.0[解析]①为假命题,集合N中最小的数是0;②为假命题,如a=不满足;③为假命题,如a=0,b=1,则a+b=1,比2小;④为假命题,所给集合中的元素不满足互异性.3.若整数a不是奇数,则a能被2整除[解析]以原命题结论的否定作条件、原命题条件的否定作结论得出逆否命题.4.既不充分也不必要[解析]取x=,y=,知充分性不成立;取x=-1,y=3,知必要性不成立.故为既不充分也不必要条件.5.若a≠0或b≠0,a,b∈R,则a2+b2≠0[解析]“若p,则q”的逆否命题为“若q,则p”,又a=b=0的实质为a=0且b=0,故其否定为a≠0或b≠0.6.对任意a,b∈R,若ab≤0,则a≤0[解析]“对任意a,b∈R”是大前提,在否命题中不变,又因为ab>0,a>0的否定分别为ab≤0,a≤0,所以原命题的否命题为“对任意a,b∈R,若ab≤0,则a≤0”.7.[-3,0] [解析]由已知可得ax2-2ax-3≤0恒成立.当a=0时,-3≤0恒成立;当a≠0时,得解得-3≤a<0.故-3≤a≤0.8.①a≥2②a<2[解析]①因为p是q的充分不必要条件,所以{x|x>a}⫋{x|x≥2},则a的取值范围是a≥2.②因为p是q的必要不充分条件,所以{x|x≥2}⫋{x|x>a},则a的取值范围是a<2.9.充分不必要[解析]依题意有p⇒r,r⇒s,s⇒q,∴p⇒r⇒s⇒q.又∵r⇒/ p,∴q⇒/ p.故p是q的充分不必要条件.【课堂考点探究】例1[思路点拨](1)根据四种命题的构成判断即可.(2)对于①②,按照要求写出相应的逆命题、否命题,再判断真假;对于③,可直接利用原命题与逆否命题的等价性判断原命题的真假;对于④,直接判断.(1)D(2)①③[解析](1)根据四种命题的构成可知,选项A,B,C均不正确.故选D.(2)①“若x+y=0,则x,y互为相反数”的逆命题为“若x,y互为相反数,则x+y=0”,显然为真命题;②否命题为“不全等的三角形的面积不相等”,而不全等的三角形的面积也可能相等,故为假命题;③原命题为真,所以它的逆否命题也为真,故③为真命题;④ab是正整数,但a,b不一定都是正整数,例如a=-1,b=-2,故④为假命题.所以答案是①③.变式题(1)B(2)①②④[解析](1)“正数a的平方不等于0”即“若a是一个正数,则它的平方不等于0”,其否命题为“若a不是正数,则它的平方等于0”,所以选B.(2)①正确,由log2(a+1)>1,得a+1>2,所以a>1,所以f(x)=log a x在其定义域内是增函数.②正确,由命题的否命题的定义知,该说法正确.③不正确,原命题的逆命题为“若(x+1)(y+1)是偶数,则x,y都是偶数”,是假命题,如(3+1)×(4+1)=20为偶数,但x=3,y=4.④正确,两者互为逆否命题,因此两命题等价.例2[思路点拨](1)将已知等式两边同时平方,可得出向量a,b的关系,从而得出结论;(2)通过研究单调性,求出函数存在零点的充要条件为a≤-1,从而得出结论.(1)C(2)B[解析](1)将|a-3b|=|3a+b|两边平方,得a2-6a·b+9b2=9a2+6a·b+b2.∵a,b均为单位向量,∴a·b=0,即a⊥b.反之,由a ⊥b可得|a-3b|=|3a+b|.故为充分必要条件.(2)因为f'(x)=>0,所以若函数f(x)=a+ln x(x≥e)存在零点,则f(e)≤0,即a≤-1,因此“函数f(x)=a+ln x(x≥e)存在零点”是“a<-1”的必要不充分条件,故选B.变式题(1)B(2)A[解析](1)当a1=-1,a2=2,公比q=-2时,虽然有a1<a2,但是数列{a n}不是递增数列,所以充分性不成立;反之,当数列{a n}是递增数列时,必有a1<a2,因此必要性成立.故选B.(2)由sin 2α-cos 2α=1得sin-=,所以2α-=2kπ+,k∈Z或2α-=2kπ+,k∈Z,即α=kπ+,k∈Z或α=kπ+,k∈Z,所以“α=”是“sin 2α-cos 2α=1”的充分而不必要条件,故选A.例3[思路点拨]直接法,分情况讨论;特例法,结合选项取特殊值验证.C[解析]方法一(直接法):当a=0时,x=-,符合题意.当a≠0时,若方程的两根为一正一负,则-⇒ ⇒a<0;若方程的两根均为负,则--⇒ ⇒0<a≤1.综上所述,所求充要条件是a≤1.方法二(排除法):当a=0时,原方程有一个负实根,可以排除A,D;当a=1时,原方程有两个相等的负实根,可以排除B.所以选C.变式题(1)B(2)[解析](1)“a>b”不能推出“a-1>b”,故选项A不是“a>b”的必要条件,不满足题意;“a>b”能推出“a+1>b”,但“a+1>b”不能推出“a>b”,故满足题意;“a>b”不能推出“|a|>|b|”,故选项C不是“a>b”的必要条件,不满足题意;“a>b”能推出“a3>b3”,且“a3>b3”能推出“a>b”,故是充要条件,不满足题意.故选B.(2)由a>0,m2-7am+12a2<0,得3a<m<4a,即p:3a<m<4a,a>0.由方程-+-=1表示焦点在y轴上的椭圆,可得2-m>m-1>0,解得1<m<,即q:1<m<.因为p是q的充分不必要条件,所以或解得≤a≤,所以实数a的取值范围是.【备选理由】例1考查对命题真假的判断,是一个开放式命题,答案不唯一,有利于学生发散思维;例2强化了充分、必要条件的判断方法和余弦定理、基本不等式的应用;例3主要考查了充要条件的判断;例4是以简单不等式的方式考查充分、必要条件的应用.例1[配合例1使用][2018·北京通州区三模]能够说明“设a,b,c是任意实数,若a>b>c,则a2>ab>c2”是假命题的一组整数a,b,c的值依次为.[答案] 1,0,-1(此题答案不唯一)[解析]当a=1,b=0,c=-1时,满足a>b>c,不满足a2>ab>c2,∴命题是假命题.故答案可以为1,0,-1.例2[配合例2使用][2018·武汉4月调研]在△ABC中,内角A,B,C的对边分别为a,b,c.已知条件p:a≤,条件q:A≤,那么p是q成立的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件[解析] A由条件p:a≤,知cos A=-≥-=-≥-=,当且仅当b=c=a时取等号,又A∈(0,π),∴0<A≤,∴A≤,即q成立.取A=,C=,B=,满足条件q,但是a>.∴p是q成立的充分而不必要条件.故选A.例3[配合例2使用][2018·莆田六中三模]在等比数列{a n}中,a2=-2,则“a4,a12是方程x2+3x+1=0的两根”是“a8=-1”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件[解析] C因为a4,a12是方程x2+3x+1=0的两根,所以a4a12=1,因此=1,又因为a2=-2<0,所以a8<0,即a8=-1.从而“a4,a12是方程x2+3x+1=0的两根”是“a8=-1”的充要条件,故选C.例4[配合例3使用][2018·南昌模拟]在实数范围内,使得不等式>1成立的一个充分而不必要条件是( )A.x>0B.x<1C.0<x<1D.0<x<[解析]D∵>1,∴-<0,∴0<x<1.∵ ⫋(0,1),∴0<x<为不等式>1成立的一个充分而不必要条件,故选D.。