切线理论与应用共42页文档

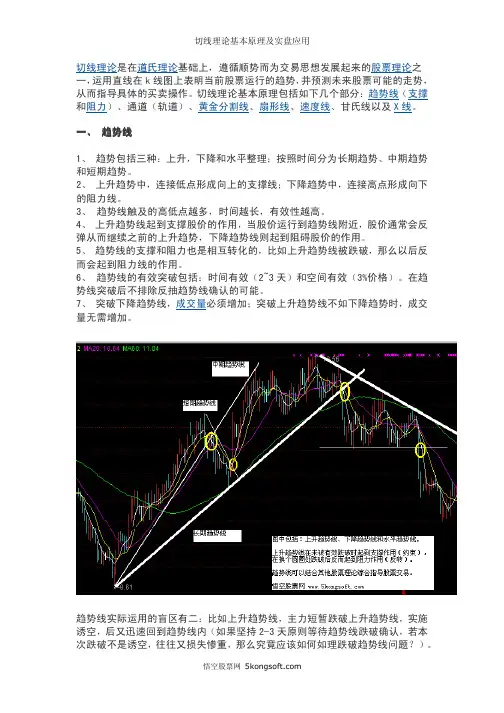
切线理论切线理论是指按一定方法和原则在由股票价格的数据所绘制的图表上画-些直线。

然后根据这些直线的情况推测股票价格的未来趋势。

一、趋势的定义简单的说，趋势就是价格的波动方向，或者说是证券市场运动的方向。

二、趋势的方向趋势的方向有三个：（1）上升方向（2）下降方向（3）水平方向三、趋势的类型趋势分为3种类型。

1、主要趋势。

主要趋势是趋势的主要方向，是投资者极力要弄清楚的目标。

了解了主要趋势才能做到顺势而为。

主要趋势是价格波动的大方向，一般持续的时间比较长。

这是技术分析第二个假设所叙述的。

2、次要趋势。

次要趋势是在进行主要趋势的过程中进行的调整。

我们知道，趋势不会一成不变的直来直去，总要局部调整和回撤的过程，次要趋势正是完成这一使命。

3、短暂趋势。

短暂趋势是在次要趋势的过程中所进行的调整。

短暂趋势与次要趋势的关系就如同次要趋势与主要趋势的关系一样。

这三种类型的趋势的最大区别是时间的长短和波动幅度的大小上的差异。

以上三种划分可以解释绝大多数的行情。

对于更复杂的价格波动过程，以上三种划分可能还不够用。

不过这不是很大的问题，可以继续对短暂趋势进行再细分。

下图是三种趋势类型的图形说明。

四、例例1此主题相关图片如下：支撑线和压力线认清趋势是进行投资的重要步骤。

认清趋势之后，就应该采取相应的行动。

如果认清大牛市已经来临，那么就应该进入市场进行实际的投资，只是将面临一个选择入市时机的问题。

每个投资者都希望在大涨之前的低点买入，或者在涨势的中途回落的低点买入。

这些低点在哪里呢？对这些问题肯定没有十全十美的答案，但是支撑线和压力线会给我们一些帮助。

一、支撑线和压力线的含义1、支撑线。

又称抵抗线。

当价格下跌到某个价位附近时，价格停止下跌，甚至可能出现回升，这是多方在这个位置买入所造成的。

这个位置对价格的继续下跌起到了迟滞作用。

这个阻止证券价格继续下跌或者暂时阻止价格继续下跌的价格位置就是支撑线所在的位置。

2、压力线。

压力线又称阻力线。

切线定理的证明与应用解析切线定理，又称为切角定理，是解析几何中的一个重要定理，用于描述平面上一条曲线与其切线的关系。

本文将对切线定理的证明及其应用进行详细的解析。

一、切线定理的证明为了证明切线定理，我们首先需要了解什么是切线以及切线的性质。

在平面几何中，给定一条曲线和曲线上的一点P，过点P且与曲线仅有一个公共点的直线称为曲线在点P处的切线。

证明切线定理的关键是利用导数的概念和性质。

假设曲线的参数方程为x=f(t)，y=g(t)，其中f(t)和g(t)分别是x和y关于参数t的函数。

取曲线上一点P(x0,y0)，并选取一条过P的切线L。

切线L的斜率可以表示为dy/dx。

由于切线仅与曲线在点P处相切，因此曲线上的其他点(x,y)也必须满足曲线方程g(x)-y=0与切线方程dy/dx(x-x0)-y+y0=0的联立条件。

通过解联立方程，我们可以得到一个关于dx和dy的方程。

对该方程进行一阶泰勒展开，可以得到一般形式的切线方程：dy/dx = [dy/dt] / [dx/dt] = g'(t) / f'(t)这个方程给出了曲线在任意一点处切线的斜率。

切线定理则是该定理的特殊情况，即当t=t0时的情况。

在切线上，有t=t0，因此切线方程简化为：dy/dx = g'(t0) / f'(t0)这个结果就是切线定理。

二、切线定理的应用切线定理在解析几何中有着广泛的应用。

下面我们将介绍切线定理在求曲线的切线、判定曲线凹凸性以及估算近似值等方面的应用。

1. 求曲线的切线通过切线定理，我们可以根据给定曲线的函数表达式，求出曲线在任意点处的切线方程。

我们只需要求出函数的导数，然后在给定点处代入即可得到切线的斜率。

再根据切线的斜率和经过给定点的条件，可以得到切线的方程。

2. 判定曲线的凹凸性对于曲线上的某一点P(x0,y0)，切线定理可以用来判定该点所在的曲线的凹凸性。

如果切线的斜率dy/dx大于零，则该点位于曲线的上凸部分；若切线的斜率小于零，则该点位于曲线的下凸部分。

切线分析及应用切线是数学中一个重要的概念，它在解析几何、微积分以及物理学等领域都有广泛的应用。

切线分析可以帮助我们更好地理解曲线的性质和行为，并且可以在实际问题中提供有用的信息和解决途径。

本文将围绕切线的定义、性质、应用以及解决实际问题的方法进行探讨。

首先，我们来回顾一下切线的定义。

给定一个函数f(x)，如果存在一点(x0, f(x0))，使得函数图像在该点处的切线通过该点且与函数图像在该点处的斜率相同，那么这条通过点(x0, f(x0))的直线就是函数f(x)在该点处的切线。

切线的斜率等于函数在该点处的导数。

切线的性质也是我们学习切线分析的基础。

首先，切线与函数图像相切于该点，意味着切线与函数曲线在该点处有且仅有一个公共点。

其次，切线在该点处与函数曲线的切点以及切线的斜率都能够提供关于函数在该点的信息。

通过切线的斜率，我们可以判断函数在该点的增减性以及函数的导数值。

通过切线与函数曲线的切点的坐标，我们可以得到函数在该点的函数值。

因此，切线不仅提供了函数在某点的局部行为的信息，还能够提供关于函数图像的整体信息。

接下来，我们来看一下切线的应用。

在几何学中，切线可以用于求解曲线与曲线之间的位置关系。

例如，给定两条曲线的方程，我们可以通过求解两条曲线的切线方程，来判断两条曲线在某点是否相切、相交或者相离。

在物理学中，切线被广泛地应用于描述物体运动的速度和加速度。

例如，在直角坐标系中，如果一个物体的位置随时间变化可以由一个函数f(x)描述，那么物体的速度可以通过求导数f'(x)得到。

物体在某时刻的瞬时速度可以通过绘制曲线f(x)在该点的切线，求解切线斜率来获得。

同样地，物体在某时刻的加速度可以通过二阶导数f''(x)求解。

利用切线的性质，我们可以得到物体在不同时刻的速度和加速度的变化规律。

切线的应用还可以延伸到其他领域。

在工程学中，我们可以利用切线来分析物体的结构强度和刚度。

通过绘制载荷-变形曲线，并求解曲线上某点的切线斜率，我们可以得到物体在该点的应力和应变。