切线理论运用

初三切线证明的技巧初三学习的数学知识中，切线的证明是一个重要的内容。

在证明切线的过程中，可以运用几何知识和代数知识，下面我将从几何和代数两个角度来介绍一些证明切线的技巧。

首先，从几何的角度来看，证明一条直线是另一条曲线的切线，通常需要利用直线与曲线的相切的性质。

在几何证明中，可以利用以下几种方法来证明切线：1. 利用切线的定义，切线是曲线在某一点处的极限位置，可以通过证明直线与曲线在该点处相切，即直线与曲线在该点处有相同的斜率。

2. 利用切线的判定定理，根据切线的定义和切线的判定定理，可以利用曲线的导数或斜率来证明直线与曲线在某一点处相切。

3. 利用几何关系，结合曲线的图形特点和直线的性质，通过观察曲线的几何形状，找出直线与曲线相切的几何关系，从而进行证明。

其次，从代数的角度来看，证明切线也可以运用代数知识和计算方法来进行。

在代数证明中，可以利用以下几种方法来证明切线：1. 利用导数，通过计算曲线在某一点的导数，可以得到曲线在该点的斜率，进而判断直线与曲线在该点处是否相切。

2. 利用函数关系，根据曲线的函数表达式，可以利用函数的性质和关系，通过计算得出曲线与直线在某一点处的相切条件。

3. 利用方程求解，通过建立曲线和直线的方程，可以通过方程的求解过程来证明直线与曲线在某一点处相切的条件。

总之，证明切线的过程需要综合运用几何和代数的知识，通过观察几何形状、计算导数和方程求解等方法来进行证明。

在初三阶段，可以通过多做相关的练习和题目，加深对切线的理解和掌握证明的技巧。

希望这些方法能够帮助你更好地理解和掌握切线的证明技巧。

切线定理的应用
切线定理是几何学中的基本定理，它对理解和解决几何问题有重要的意义。

它告诉我们，两条直线总可以用一条切线将它们分开，而且这条切线可在原来的两条直线上取得一定数量的点。

切线定理的实际应用范围广泛，不仅在几何学中有着重要的地位，还在许多其它方面发挥着重要作用。

首先，它可以用来解决经典的几何问题，比如两个圆的外切及内切等问题。

其次，它可以帮助我们理解现实问题，例如求解商业类的问题，举例来说，由线段和圆的关系，可以帮助人们更好地理解商品的经济学习。

此外，切线定理还可以应用于最优化问题，以实现更有效率和更低成本的生产，这类问题在企业管理和技术研发中占有重要地位。

切线定理可以有效解决几何图形的最佳组合问题，从而在减少成本的同时，提高生产的效率。

另外，切线定理也在军事理论中被广泛运用，比如用切线定理来分析对敌人战术的最佳突破方法，形成最有效的战略以及设计最有效率的部署等等。

不管是在数学几何学中还是在其他实际应用中，切线定理都发挥着重要的作用，它为我们解决许多繁杂的问题提供了科学的技术支持，并使科学研究取得了重大的进步。

总之，切线定理是一种重要的定理，它对理解和解决几何问题，以及应用于企业管理，军事理论，最优化等方面，都发挥着重要的作用。

它的完备性给了我们更多的可能性，可以帮助我们研究未知的世
界，有效地解决问题，推动科学的发展。

切线定理的应用切线定理是欧几里得几何学的一种基本定理，它说明了椭圆的形状，虽然在几何中有很多样式，但是它是一个拥有较好性质的曲线，也是拥有许多重要应用的曲线。

在空间几何中，切线定理常用于求解平面曲线的内关，这些曲线可以是圆，椭圆，抛物线等等。

他们之间关于曲线上点的切线的关系都可以用切线定理来描述。

在几何中，切线定理的简单形式可以看作是有关圆的定理，即所有经过圆心的直线，切点在圆上的切线条数都相等。

同样地，椭圆上切点在椭圆上的切线条数也是相等的。

此外，它还可以用来证明抛物线在（x，0）点的切线条数为2，在（0，y）点的切线条数为3。

此外，切线定理也可以用于求解曲线圆心角，其中，圆心角是一种经典的概念，它指的是两曲线在相同的点处的切线的夹角，也就是说，它可以用来描述两个曲线的相交情况。

如果椭圆的两个切点之间的夹角为α，那么由切线定理可以得出：α=2 arctan（a / b），其中a和b分别是椭圆的长轴和短轴的长度。

此外，切线定理在微积分中也有重要的应用，其中应用最为广泛的是椭圆积分（Elliptic Integral）。

根据定义，椭圆积分是一种对椭圆曲线上一点求出积分值，以此来求出椭圆曲线两点之间的面积。

而切线定理可以用来证明椭圆积分在一般情况下的计算公式，从而提供了一种更容易求解椭圆积分的方法。

总之，切线定理是几何学中一种重要的定理，它对几何学的发展有着重要的意义，也在许多学科中都有重要的应用。

切线定理在几何中的运用有利于求解椭圆曲线，圆心角和抛物线。

此外，它也在微积分中有重要应用，可以用来计算椭圆积分，让计算更为简单、准确。

由此可见，切线定理是一种非常重要的定理，广泛应用于许多学科中，可谓秉承了具有极大价值的数学理论。

切线理论简介与应用一、趋势分析简单地说，趋势就是股票价格的波动方向，或者说是股票市场运动的方向。

趋势的方向有三个：a.上升方向；b.下降方向；c.水平方向，也就是无趋势方向。

按道氏理论的分类，趋势分为三个类型：主要趋势、次要趋势和短暂趋势。

支撑线和压力线1.支撑线和压力线的作用支撑线(surport line)又称为抵抗线。

当股价跌到某个价位附近时，股价停止下跌，甚至有可能还有回升。

这个起着阻止股价继续下跌或暂时阻止股价继续下跌的价格就是支撑线所在的位置。

压力线(resistance line)又称为阻力线。

当股价上涨到某价位附近时，股价会停止上涨，甚至回落。

这个起着阻止或暂时阻止股价继续上升的价位就是压力线所在的位置。

支撑线和压力线的作用是阻止或暂时阻止股价向一个方向继续运动。

同时，支撑线和压力线又有彻底阻止股价按原方向变动的可能。

2.支撑线与压力线相互转化一条支撑线如果被跌破，那么这个支撑线将成为压力线；同理，一条压力线被突破，这个压力线将成为支撑线。

这说明支撑线和压力线的地位不是一成不变的，而是可以改变的，条件是它被有效的足够强大的股价变动突破。

3.支撑线和压力线的确认和印正一般来说，一条支撑线或压力线对当前影响的重要性有三个方面的考虑，一是股价在这个区域停留时间的长短；二是股价在这个区域伴随的成交量大小；三是这个支撑区域或压力区域发生的时间距离当前这个时期的远近。

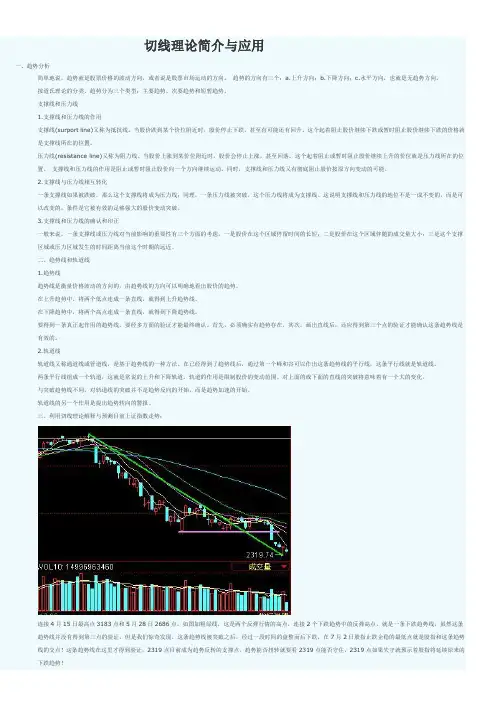
二、趋势线和轨道线1.趋势线趋势线是衡量价格波动的方向的，由趋势线的方向可以明确地看出股价的趋势。

在上升趋势中，将两个低点连成一条直线，就得到上升趋势线。

在下降趋势中，将两个高点连成一条直线，就得到下降趋势线。

要得到一条真正起作用的趋势线，要经多方面的验证才能最终确认。

首先，必须确实有趋势存在。

其次，画出直线后，还应得到第三个点的验证才能确认这条趋势线是有效的。

2.轨道线轨道线又称通道线或管道线，是基于趋势线的一种方法。

在已经得到了趋势线后，通过第一个峰和谷可以作出这条趋势线的平行线，这条平行线就是轨道线。

切线理论的应用原理什么是切线理论？切线理论是一种数学理论，它描述了曲线上某一点的切线与曲线的关系。

在微积分中，我们学过了如何求曲线的切线斜率，通过切线斜率我们可以得到曲线在某一点的切线方程。

切线理论不仅在数学中有着重要的应用，同样在物理、工程、计算机图形学等领域也有广泛的应用。

切线理论的应用原理1. 图像处理中的边缘检测在图像处理中，边缘检测是一个非常重要的处理步骤。

通过检测图像中的边缘，我们可以提取出物体的轮廓。

而边缘通常就是曲线的切线部分。

通过切线理论，我们可以找到图像中各个点的切线，从而得到边缘的位置和方向。

2. 机器人的导航在机器人的导航中，切线理论也扮演着重要的角色。

当机器人行进到某一点时，它需要根据当前位置的切线方向来确定下一步的行进方向。

切线方向可以通过初始位置和机器人的速度来确定，进而指导机器人的运动。

3. 自动驾驶的轨迹规划在自动驾驶系统中，切线理论被广泛应用于轨迹规划。

切线理论可以帮助我们确定车辆行驶的最佳路径，并通过确定路径上各点的切线方向来指导车辆的转向。

通过切线理论，自动驾驶系统可以在无人驾驶过程中更加精确地控制车辆的行驶轨迹。

4. 物理学中的力学分析在物理学中，切线理论是力学分析中的重要基础。

在求解物体受力过程中的运动轨迹时，我们需要考虑物体所受到的切线方向的力。

切线方向的力可以影响物体的运动速度和运动方向，进而影响物体的最终运动结果。

5. 计算机图形学中的曲线绘制在计算机图形学中，我们常常需要绘制各种各样的曲线。

切线理论可以帮助我们确定曲线上各点的切线方向，从而使得曲线的绘制更加精确和自然。

通过切线理论，我们可以绘制出平滑和流畅的曲线，提高图形的质量和观赏性。

总结切线理论作为一种数学理论，在科学与工程领域中有着广泛的应用。

无论是在图像处理、机器人的导航、自动驾驶的轨迹规划、物理学的力学分析，还是计算机图形学中的曲线绘制，切线理论都能够发挥重要的作用。

通过切线理论，我们可以更加准确地分析和理解曲线上的各种现象，从而推动科学与技术的发展。

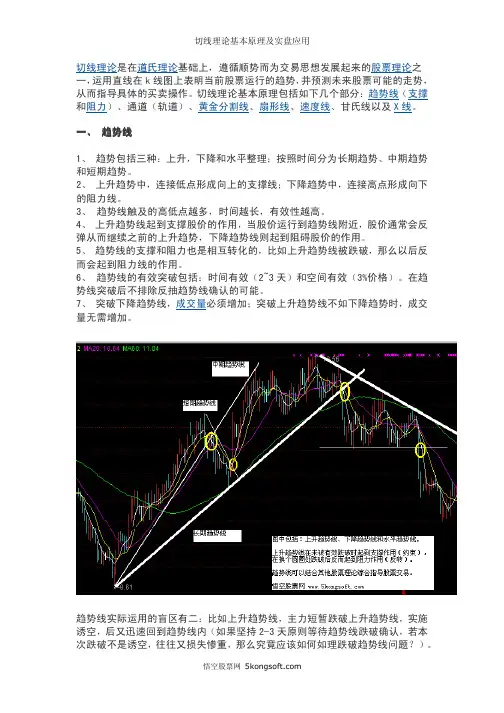
切线理论-实盘应用解析切线理论-实盘应用解析切线理论包括趋势线、通道、黄金分割线等,能够帮助股民认清股票趋势的延续和逆转。

下面是切线理论的实盘应用要点和图解。

1、单趋势线:向上突破下降趋势线时a.应谨慎看多不宜马上介入,应等待第二个低点的产生,形成上升趋势,才是介入良机。

并且以两个低点的连线所作的上升趋势线作为止损点。

b.若突破后即行介入,应以下降压力线或前期低点或颈线作为止损价。

2、单趋势线:向下突破上升趋势线时:a.突破后立即退出,如短期内返身向上再次进入通道内部,则应在回调受到新趋势线支撑后介入(很多股票短线诱空采取这种方式)。

b.突破后立即退出,如形成整理走势,待突破整理形态压力线时再行介入。

3、组合趋势线a.慢速上升趋势线快速上升趋势线:当前运行在快速通道,下方支撑被跌破,短线应该出局,待股价缩量调整到慢速上升趋势线支撑处考虑介入。

b.慢速下降趋势线短期上升趋势线(反弹):维持在该上升趋势线上方时少量介入,股价反弹至慢速下降趋势线附近考虑获利了结,或股价跌破该上升趋势线清仓。

c.慢速下降趋势线快速下降趋势线:股价在快速下降趋势线下方时观望,若反弹突破快速下降趋势线,谨慎少量做多。

4、通道的预警与测量a.如果在一次波动中未触及到轨道线,离得很远就开始掉头,这往往是原有趋势将要改变的信号,因为市场已经没有力量继续维持原有的上升或下降的规模b.上升通道,股价连续在通道下沿附近盘整,频繁短期跌破支撑,股价最终很可能会跌破该通道支撑。

测量:不管突破哪一条价格边线或以何种方式突破,沿突破方向所做的与原通道等宽的外延平行线即为股价的最小运动幅度。

5、通道的突破(加速还是衰竭?)例.上升通道上方压力线被突破,已有仓位继续持有,没有的仓位的要依据大盘、个股具体情况及突破有效性决定是否介入:以下因素综合考虑得出结论:已有通道角度本身已经非常陡峭,股票短线涨幅巨大,则诱多可能很大。

突破发生后股价是否能保持在通道之外?如果价格突破后能保持在通道之外,就可能出现加速运动。

切线的名词解释切线是几何学中一个重要的概念，它是与曲线相切的直线。

在数学和物理学中，切线被广泛应用于解决问题和推导新的理论。

本文将探讨切线的定义、性质以及在不同学科中的应用。

1. 切线的定义与性质切线是曲线在某一点处与曲线相切的直线。

它具有以下性质：1.1 切线与曲线相交于一点：切线只与曲线在某一特定点相交，这个点称为切点。

切点是曲线上具有与切线相同斜率的点。

1.2 切线的斜率等于曲线在切点处的导数：切线的斜率等于曲线在切点处的导数。

这是切线定义的重要性质。

导数可以理解为曲线的变化率，因此切线的斜率可以告诉我们曲线在切点处的变化趋势。

1.3 切线是曲线的局部近似：切线是曲线在切点附近的一段局部近似。

当切点与曲线的距离越近，切线越能准确地代表曲线的形状。

2. 切线在数学中的应用2.1 曲线的切线方程：利用切线的定义和性质，我们可以推导出曲线的切线方程。

对于已知曲线方程y = f(x)，我们可以通过求导得到曲线的导函数f'(x)，然后使用切线的斜率公式，在切点(x0, f(x0))处得到切线的斜率。

再结合切线与曲线的相交条件，可以得到切线方程y - f(x0) = f'(x0)(x - x0)。

切线方程可以在计算和解析几何中帮助我们理解曲线的性质。

2.2 切线的切点坐标求解：切线与曲线相交于切点，求解切点的坐标是数学中常见的问题。

一种常用的方法是联立切线方程和曲线方程，通过求解方程组来确定切点的坐标。

这个过程需要运用代数解方程的技巧，帮助我们更好地理解曲线与切线的关系。

3. 切线在物理学中的应用3.1 切线与力的方向：在物理学中，切线被广泛应用于解释物体运动过程中力的方向。

根据牛顿第二定律，物体受力后会产生加速度。

在曲线运动中，物体运动轨迹的切线方向可以表示物体受力的方向。

例如，当物体在向心力作用下沿着圆周运动时，切线方向指向圆心，表示向心力的方向。

3.2 切线与速度的关系：在物理学中，切线还与速度有密切关系。

技术分析系列教程15切线理论趋势线蒲博函趋势线是技术分析中常用的工具之一，它可以帮助我们识别价格走势的方向和趋势的强弱。

切线理论是一种关于趋势线的建立和应用的理论方法，它能够更准确地确定趋势线，提供更详细的交易信息。

切线理论中的切线是通过连接价格走势中的关键极点来绘制的。

关键极点是指价格走势中的高点或低点，它们代表了市场情绪的变化和供需力量的转移。

通过连接这些关键极点，我们可以得到趋势线，从而确定市场的趋势和阻力支撑位。

切线理论的应用方法主要有三种：1.切线趋势线的构建；2.切线的角度；3.切线的平行线。

首先，切线趋势线的构建是通过连接价格走势中的两个或多个关键极点来绘制趋势线。

关键极点的选择要基于价格走势的重要转折点，如高点和低点。

我们可以通过观察价格走势的波动和关键极点之间的关系来确定趋势线的位置和走势。

其次，切线的角度可以帮助我们判断趋势的强弱和趋势的变化。

当切线的角度较大时，说明趋势较为明显和强劲；当切线的角度较小或接近水平线时，说明趋势较为弱势或可能发生反转。

因此，我们可以通过观察切线的角度来进行交易决策，如确认趋势的延续或逆势交易。

最后，切线的平行线可以帮助我们确定阻力和支撑位的位置。

一般来说，当价格上升或下跌时，我们可以通过绘制与切线平行的线来确定未来的阻力和支撑位。

这些平行线可以作为我们的交易目标和止损位的参考。

总体而言，切线理论是一种实用的技术分析工具，它可以帮助我们更准确地确定趋势线的位置和走势。

通过切线理论的应用，我们可以提高交易的胜算，降低风险，实现更稳定的盈利。

然而，切线理论也需要结合其他技术指标和交易策略来使用，以提高分析的准确性和可靠性。

在实际应用中，我们可以通过选取合适的时间周期和合理设置止损位来综合考虑切线理论与其他技术指标的综合效果。

此外，我们还应该时刻关注市场的变化和风险，及时调整交易策略和止损位，以保证交易的稳定性和盈利能力。