- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.已知二元一次方程3x-2y=5,若y=0,则x=
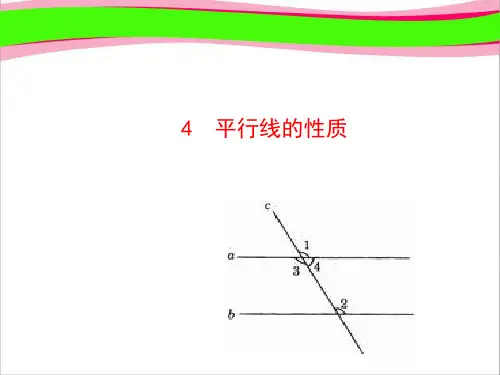
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且
∠1=∠2.求证:a∥b.
证明:∵∠1=∠2 (已知), ∠1+∠3=180°(平角的定义).
c
a
13
∴∠2+∠3 = 180°(等量代换).
b
2
∴∠2与∠3互补(互补的意义).
∴ a∥b(同旁内角互补,两直线平行).
把你所悟到的证明一个命题的方法,步骤,书写格式以及
【解析】 8 个人去看电影 x+y=8 每张成人票 5 元
每张儿童票 3 元
买5x票+花3y了=3344 元
定义:
x-y=2
x+y=8
x+1=2(y-1)
5x+3y=34
上面所列方程各含有几个未知数? 答:2个未知数
答:次数是1 含有未知数的项的次数是多少?
含有两个未知数,并且所含未知数的项的次数都是1
言论的花,开得愈大;行为的果子,结得愈小。 ——冰心
第五章 二元一次方程组
1 认识二元一次方程组
1.了解二元一次方程、二元一次方程组及其解等有关概 念,并会判断一组数是不是某个二元一次方程组的解.
2.通过讨论和练习,进一步培养学生观察、比较、分析 的能力.
3.通过对实际问题的分析,使学生进一步体会方程是刻 画现实世界的有效数学模型,培养学生良好的数学应用 意识.
已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内 角,且∠1与∠2互补.求证:a∥b
c
a
1
b2
3
证明:∵ ∠1与∠2互补 (已知), ∴∠1+∠2=180°(互补的定义). ∴∠1= 180°-∠2(等式的性质). 又∵∠3+∠2=180° (平角的定义), ∴∠3= 180°-∠2(等式的性质). ∴∠1=∠3(等量代换). ∴ a∥b(同位角相等,两直线平行). 已给的公理,定义和定理以后都可以作为依据,用来证明 新的命题. 说说你所悟到的证明一个命题的方法,步骤,书写格式以 及注意事项.
你还累?这么大的 个,才比我多驮 了2个.
哼,我从你背上拿来 1个,我的包裹数就 是你的2倍!
真的?!
我从你背上拿来 1个,我的包裹数 就是你的 2 倍!
你还累?这么大 的个,才比我 多驮了2个.
它们各驮了多少包裹呢?
【解析】设老牛驮了 x 个包裹 , 小马驮了 y个包裹. 老牛的包裹数比小马的多2个,
4.(铜仁·中考)如图,请填写一个你认为恰当的条件 ______,使AB∥CD.
【解析】此题答案不唯一,填写的条件可以是∠CDA= ∠DAB或∠PCD=∠BAC或∠BAC+∠ACD=180°等.
答案:答案不唯一,如∠CDA=∠DAB
通过本课时的学习,需要我们掌握: 1.两条直线被第三条直线所截,会产生同位角、内错角、 同旁内角.角的关系决定了两条直线是否平行,因此在做 题时要掌握好“三线八角”; 2.同位角相等、内错角相等,两直线平行;同旁内角互 补两直线平行.
3, 1
不是原方程组的解;
(3)把x=4,y
1 2
代入方程①,
②,发现能使方程
x 4,
y
1. 2
①, ②左右两边相等,所以
是原方程组的解.
【跟踪训练】
把下列方程组的解和相应的方程组用线段连起来:
x=1,
y=3-x,
y=2. x=3, y=-2. x=2, y=1.
y3=x2+x2,y=8. x+y=3. y=1-x, 3x+2y=5.
么令人惊奇,小小的蜜蜂在人类有史以前就已经解决了的问题,十
八世纪的数学家竟要用高等数学才能解决!
想一想
数学就在我们身边!
β
β
蜂房的底部由三个全等的四边形围成, 每个四边形的形状如图所示,其中 ∠α =109°28′, ∠β =70°32′. 试确定这三个四边形的形状,并说明你 的理由.
解:平行四边形.理由如下: ∵∠A+∠D=180° ∴ AB∥CD. 同理可证:AD∥BC. ∴ ABCD为平行四边形. 即所求三个四边形为平行四边形.
哦……我忘了!只记得 先后买了两次,第一次 买了5支笔和10本笔记 本花了42元钱,第二次 买了10支笔和5本笔记 本花了30元钱.
4 5
5.已知2x+3y=4,当x=y 时,x,y的值为_____,当x+y=0时,
-4
4
1
x=_____x,=-y3=______.
2
y=-2
6.已知-1
8
是方3 程2x-4y+2a=3的一个解,则a=______.
议一议
据说,人类知识的75%是在操作中学到的. 小明用下面的方法作出平行线,你认为他的作法对吗? 为什么?
通过这个操作活动,得到了什么结论?
定理 两条直线被第三条直线所截,如果内错角相等,那 么这两条直线平行. 这个定理可以简单说成:内错角相等,两直线平行. 你能运用所学知识来证实它是一个真命题吗?
1.什么叫方程? 含有未知数的等式叫做方程. 如: 2x+3=5, x+y=8.
2.什么叫一元一次方程? 在一个方程中,只含有一个未知数,且未知数的指数都是
1,这样的方程叫做一元一次方程.
如: 2x+3=5, y+6=8. 3.解下列方程:
(1)3x+2=14 (2)2x-4=14-xFra bibliotek累死我了!
x=5 ,y =3是否为方程 x+y=8的一个解? x=5 , y =3是否为方程 5x +3y=34的一个解? 二元一次方程组中各个方程的公共解,叫做这个二元一 次方程组的解.
x=5
{ 例如
就是二元一次方程组 y=3
{ x+y=8 5x+3y=34
的解
【例题】
x 4y 6, ①
【例】检验下列各对数是不是方程组 3x 2y 11 ② 的解.
注意事项内化为一种方法.
借助“同位角相等,两直线平行”这一公理,你还能证明
哪些熟悉的结论?
【跟踪训练】
如图:直线AB、CD都和AE相交,且 ∠1+∠A=180°. 求证:AB//CD
A
B
2
C
13
D
E
证明:∵∠1+∠3=180°(1平角=180°), ∠2+∠3=180°( 1平角=180°), ∴∠1=∠2(等量代换). ∵∠1+∠A=180°( 已知 ), ∴∠2+∠A=180°(等量代换).
x+ y =1 B.
x-y=1
x=1 C.
y+x=2
6x+4y=9 D.
y=1
y=3x+4
4.(嘉兴·中考)根据以下对话,可以求得小红所买的 笔和笔记本的价格分别是( D )
小红,你上周买的笔和笔 记本的价格是多少啊?
A.0.8元/支,2.6元/本 B.0.8元/支,3.6元/本 C.1.2元/支,2.6元/本 D.1.2元/支,3.6元/本
(每个角都是120°),而它的尖顶形成的底部则都是由三个完全相
同的菱形拼接而成的.十八世纪初,法国学者马拉尔其经过测量发现,
所有的底部菱形的钝角都等于109°28′,而其锐角都等于70°32′。
法国物理学家列奥缪拉由这个有趣的发现得到一个启示:蜂房的这
一特殊形状,可能是为了保证得到同样大的容积而所用材料最省.多
x 2,
(1)
y
1.
x 3,
x 4,
(2)
y
1.
(3)
y
1 2
.
解:(1)把x=2,y=1分别代入方程①,②,发现不满足②,所以
x 2,
y
1
不是原方程组的解;
(2)把x=3,y=-1代入方程①,②,发现不满足①,所以
x
y
3 平行线的判定
1.能根据“同位角相等,两直线平行”证明“同旁内角 互补,两直线平行”“内错角相等,两直线平行”,并 能简单地应用这些结论. 2.初步了解证明的基本步骤和书写格式. 3.体会几何中推理的严谨性、书写的规范性,发展初步 的演绎推理能力.
请找出图中的平行线! 它们为什么平行?
公理 两条直线被第三条直线所截,如果同位角相等, 那么这两条直线平行. 简单说成:同位角相等,两直线平行 你认为“两条直线被第三条直线所截,如果同旁内角互 补,那么这两条直线平行”这个命题正确吗?说明理由.
∴AB‖CD ( 同旁内角互补,两直线平行 )
你还有其他证明方法吗?
平行线的判定方法
公理:
c
同位角相等,两直线平行.
a
1
∵ ∠1=∠2, ∴ a∥b.
b
2
判定定理1:
内错角相等,两直线平行.
a
∵ ∠1=∠2, ∴ a∥b.
b
判定定理2:
同旁内角互补,两直线平行. a
∵∠1+∠2=180°, ∴ a∥b. b
的方程叫做二元一次方程.
【跟踪训练】
下列方程中哪些是二元一次方程
(1) x+y+z=9
(2) x=6
√ (3) 2x+6y=14 √
(4) xy+y=7
(5) 7x+6y+4=16
(6) x²+y=6
x,y所代表的对象分别相同,因而x,y必须同时满足方程 x+y=8和5x+3y=34 ,把它们联立起来,得:
x+y=8 5x+3y=34 像这样共含有两个未知数的两个一次方程所组成的一组 方程,叫做二元一次方程组.