透明薄膜厚度的测量

测量薄膜厚度的方法一、引言薄膜广泛应用于电子、光学、材料等领域，因此准确测量薄膜的厚度对于质量控制和产品性能评估至关重要。

本文将介绍几种常用的测量薄膜厚度的方法。

二、显微镜法显微镜法是一种常见的测量薄膜厚度的方法。

通过显微镜观察薄膜表面的颜色变化，利用颜色与厚度之间的关系确定薄膜的厚度。

这种方法非常简单易行，但对于颜色辨识的要求较高，且只适用于透明的薄膜。

三、椭偏仪法椭偏仪法是一种基于光学原理的测量方法。

通过测量薄膜对光的旋光性质，可以推算出薄膜的厚度。

椭偏仪法具有高精度和较大的测量范围，在光学薄膜领域得到广泛应用。

四、干涉法干涉法是一种基于光学干涉原理的测量方法。

利用光的干涉现象，通过测量干涉条纹的特征，可以推断薄膜的厚度。

常见的干涉法有菲涅尔反射干涉法、Michelson干涉法等。

干涉法具有高精度和无损测量的特点，被广泛应用于光学薄膜的测量。

五、X射线衍射法X射线衍射法是一种非常常用的测量薄膜厚度的方法。

通过将X射线照射到薄膜上，根据衍射光的特征，可以计算出薄膜的厚度。

X 射线衍射法具有非常高的精度和广泛的适用范围，被广泛应用于材料科学和工程领域。

六、扫描电子显微镜法扫描电子显微镜法是一种通过扫描电子束与样品的相互作用来测量薄膜厚度的方法。

通过扫描电子显微镜观察样品表面的形貌变化，可以推算出薄膜的厚度。

这种方法具有高分辨率和较大的测量范围，被广泛应用于材料科学和纳米技术领域。

七、原子力显微镜法原子力显微镜法是一种通过探针与样品表面的相互作用来测量薄膜厚度的方法。

通过原子力显微镜观察样品表面的拓扑特征，可以计算出薄膜的厚度。

原子力显微镜法具有非常高的分辨率和较大的测量范围，广泛应用于纳米技术和表面科学领域。

八、总结本文介绍了几种常用的测量薄膜厚度的方法，包括显微镜法、椭偏仪法、干涉法、X射线衍射法、扫描电子显微镜法和原子力显微镜法。

这些方法各有优劣，应根据实际需求选择合适的方法进行测量。

在实际操作中，还需注意操作规范和仪器校准，以确保测量结果的准确性和可靠性。

近代物理实验椭圆偏振仪—薄膜厚度测量本实验所用的反射式椭偏仪为通常的PCSA 结构，即偏振光学系统的顺序为起偏器（Polarizer ）→补偿器（Compensator ）→样品（Sample ）→检偏器（Analyzer ），然后对其输出进行光电探测。

一．实验原理1． 反射的偏振光学理论图1 光在界面上的反射，假定21n n <，B ϕϕ<1（布儒斯特角），则rs E 有π的相位跃变，光在两种均匀、各向同性介质分界面上的反射如图1所示，单色平面波以入射角1ϕ，自折射率为1n 的介质1射到两种介质的分界面上，介质2的折射率为2n ，折射角2ϕ。

用（is ip E E ,），（rs rp E E ,），（ts tp E E ,）分别表示入射、反射、透射光电矢量的复振幅，p 表示平行入射面即纸面的偏振分量、s 表示垂直入射面即垂直纸面的偏振分量，每个分量均可以表示为模和幅角的形式)exp(||ip ip ip i E E β=，)exp(||is is is i E E β= （1a ） )exp(||rp rp rp i E E β=，)exp(||rs rs rs i E E β= （1b ） )exp(||tp tp tp i E E β=，)exp(||ts ts ts i E E β=（1c ） 定义下列各自p ，s 分量的反射和透射系数：ip rp p E E r /=，is rs s E E r /=（2a ） ip tp p E E t /=，is ts s E E t /=（2b ） 根据光波在界面上反射和折射的菲涅耳公式：21122112cos cos cos cos ϕϕϕϕn n n n r p +-=（3a ） 22112211cos cos cos cos ϕϕϕϕn n n n r s +-=（3b ） 211211cos cos cos 2ϕϕϕn n n t p +=（3c ） 221111cos cos cos 2ϕϕϕn n n t s +=（3d ） 利用折射定律：2211sin sin ϕϕn n =（4） 可以把式（3a ）-（3d ）写成另一种形式)()(2121ϕϕϕϕ+-=tg tg r p(5a) )sin()sin(2121ϕϕϕϕ+--=s r（5b ） )cos()sin(sin cos 2212121ϕϕϕϕϕϕ-+=p t（5c ）)sin(sin cos 22121ϕϕϕϕ+=s t （5d ） 由于折射率可能为复数，为了分别考察反射对于光波的振幅和位相的影响，我们把p r ，s r 写成如下的复数形式：)exp(||p p p i r r δ= （6a ） )exp(||s s s i r r δ= （6b ） 式中||p r 表示反射光p 分量和入射光p 分量的振幅比，p δ表示反射前后p 分量的位相变化，s 分量也有类似的含义，有ip p rp E r E = （7a ）is s rs E r E = （7b ）定义反射系数比G ：s pr r G = （8）则有: is ip rs rpE E G E E = （9）或者由式（1）式，)](exp[||||)](exp[||||is ip is ip rs rp rs rp i E E G i E E ββββ-=- （10）因为入射光的偏振状态取决于ip E 和is E 的振幅比||/||is ip E E 和位相差（is ip ββ-），同样反射光的偏振状态取决于||/||rs rp E E 和位相差（rs rp ββ-），由式（10），入射光和反射光的偏振状态通过反射系数比G 彼此关联起来。

膜厚检测记录范文一、检测背景膜厚是指薄膜材料在一个特定位置上的厚度，是薄膜工艺中的一个重要参数。

膜厚的准确度对于保证薄膜产品的性能、稳定性和可靠性具有关键作用。

因此，进行膜厚检测是非常必要的。

二、检测方法膜厚的检测方法有多种，常见的包括光学显微镜法、扫描电子显微镜法、X射线荧光光谱法等。

本次膜厚检测采用了光学显微镜法。

三、检测仪器本次膜厚检测使用的仪器是XX牌光学显微镜，该仪器具有高分辨率、高放大倍数和高精确度的特点，能够对薄膜进行准确的膜厚测量。

四、检测样品本次膜厚检测的样品为一种透明薄膜材料，材料厚度在10μm左右。

样品尺寸为10mm x 10mm。

五、检测步骤1.将样品放置在检测台上，并确保样品平整无褶皱和气泡。

2.使用微调装置调整显微镜的焦距，确保图像清晰可见。

3.调整显微镜的放大倍数，使得样品的图像适合观察。

4.在膜片的几个不同位置上进行测量。

选取代表性位置进行测量即可。

5.使用显微镜测量软件进行膜厚的测量，记录测量结果。

六、检测结果经过测量，测得样品的膜厚如下：位置1：12.3μm位置2：11.8μm位置3：11.9μm位置4：12.1μm位置5：12.0μm平均膜厚：12.02μm七、检测结论根据本次膜厚检测的结果，样品的平均膜厚为12.02μm，符合设计要求。

膜厚测量的结果可靠，可以保证样品的质量和性能。

但仍需注意，在生产过程中应对膜厚进行频繁的监测和测量，以确保薄膜产品的稳定性和一致性。

八、检测记录时间：XXXX年XX月XX日检测人员：XXX检测仪器：XX牌光学显微镜检测结果：位置1：12.3μm位置2：11.8μm位置3：11.9μm位置4：12.1μm位置5：12.0μm平均膜厚：12.02μm检测结论：经检测，样品膜厚符合设计要求，测量结果准确可靠。

以上便是本次膜厚检测的记录，检测结果表明样品的膜厚符合要求，可实现预期的功能和效果。

膜厚检测的重要性需要在生产过程中高度重视，以保证产品的质量和性能。

103实验十二 用椭偏仪测薄膜厚度与折射率随着半导体和大规模集成电路工艺的飞速发展，薄膜技术的应用也越加广泛。

因此，精确地测量薄膜厚度与其光学常数就是一种重要的物理测量技术。

目前测量薄膜厚度的方法很多。

如称重法、比色法、干涉法、椭圆偏振法等。

其中，椭圆偏振法成为主要的测试手段，广泛地应用在光学、材料、生物、医学等各个领域。

而测量薄膜材料的厚度、折射率和消光系数是椭圆偏振法最基本，也是非常重要的应用之一。

实验原理由于薄膜的光学参量强烈地依赖于制备方法的工艺条件，并表现出明显的离散性，因此，如何准确、快速测量给定样品的光学参量一直是薄膜研究中一个重要的问题。

椭圆偏振法由于无须测定光强的绝对值，因而具有较高的精度和灵敏度，而且测试方便，对样品无损伤，所以在光学薄膜和薄膜材料研究中受到极大的关注。

椭圆偏振法是利用椭圆偏振光入射到样品表面，观察反射光的偏振状态（振幅和位相）的变化，进而得出样品表面膜的厚度及折射率。

氦氖激光器发出激光束波长为632.8nm 的单色自然光，经平行光管变成单色平行光束，再经起偏器P 变成线偏振光，其振动方向由起偏器方位角决定，转动起偏器，可以改变线偏振光的振动方向，线偏振光经1/4波片后，由于双折射现象，寻常光和非寻常光产生π/2的位相差，两者的振动方向相互垂直，变为椭圆偏振光，其长、短轴沿着1/4波片的快、慢轴。

椭圆的形状由起偏器的方位角来决定。

椭圆偏振光以一定的角度入射到样品的表面，反射后偏振状态发生改变，一般仍为椭圆偏振光，但椭圆的方位和形状改变了。

从物理光学原理可以知道，这种改变与样品表面膜层厚度及其光学常数有关。

因而可以根据反射光的特性来确定膜层的厚度和折射率。

图1为基本原理光路。

图2为入射光由环境媒质入射到单层薄膜上，并在环境媒质——薄膜——衬底的两个界面上发生多次折射和反射。

此时，折射角满足菲涅尔折射定律332211sin sin sin ϕϕϕN N N ==(1)104 其中N 1，N 2和N 3分别是环境媒质、= n – i k ）；ϕ1为入射角、 ϕ2 和ϕ3分别为薄膜和衬底的折射角。

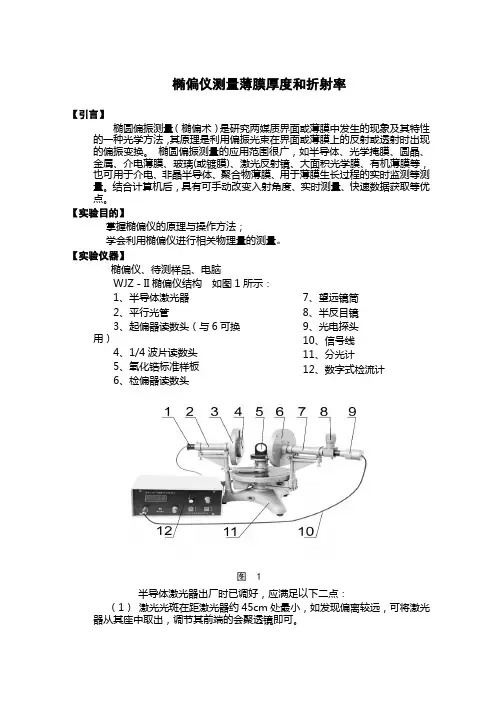
椭偏仪测量薄膜厚度和折射率【引言】椭圆偏振测量（椭偏术）是研究两媒质界面或薄膜中发生的现象及其特性的一种光学方法，其原理是利用偏振光束在界面或薄膜上的反射或透射时出现的偏振变换。

椭圆偏振测量的应用范围很广，如半导体、光学掩膜、圆晶、金属、介电薄膜、玻璃(或镀膜)、激光反射镜、大面积光学膜、有机薄膜等，也可用于介电、非晶半导体、聚合物薄膜、用于薄膜生长过程的实时监测等测量。

结合计算机后，具有可手动改变入射角度、实时测量、快速数据获取等优点。

【实验目的】掌握椭偏仪的原理与操作方法；学会利用椭偏仪进行相关物理量的测量。

【实验仪器】椭偏仪、待测样品、电脑WJZ－II椭偏仪结构如图1所示：1、半导体激光器2、平行光管3、起偏器读数头（与6可换用）4、1/4波片读数头5、氧化锆标准样板6、检偏器读数头7、望远镜筒8、半反目镜9、光电探头10、信号线11、分光计12、数字式检流计图 1半导体激光器出厂时已调好，应满足以下二点：（1）激光光斑在距激光器约45cm处最小，如发现偏离较远，可将激光器从其座中取出，调节其前端的会聚透镜即可。

（2） 激光与平行光管共轴，如发现已破坏，请按第8页“光路调整”中所述方法进行调整，一旦调好，轻易不要将其破坏。

主要技术性能及规格 1. 测量透明薄膜厚度范围0－300nm ，折射率1.30－2.49。

2. 起偏器、检偏器、1/4波片刻度范围0°-360°，游标读数0.1°。

3. 测量精度：±2nm 。

4. 入射角ψ1＝70°，K9玻璃折射率n ＝1.515。

5. 消光系数：0，空气折射率1。

6. *JGQ －250氦氖激光器波长λ＝632.8nm （用软件处理数据时，该波长值已内嵌，无须输入）。

*半导体激光器波长λ＝635nm （用软件处理数据时，该波长值未内嵌，须输入，并需重新设置消光系数“0”） 7. 椭圆偏振仪的简介：随着科学和技术的快速发展，椭偏仪的光路调节和测量数据的处理越来越完善快捷。

中图分类号 :O43 文献标识码 :A文章编号 :1001 - 2443 (2012) 01 - 0032 - 03薄膜材料具有不同于体材料的特殊性质 ,因而在集成电路工艺中有着广泛的应用. 各种薄膜材料 ,包括 半导体 、金属和绝缘体薄膜可以作为器件的功能层1 ,或作为电极2 ,或者作为钝化层保护器件免受环境的影响等等. 薄膜的质量对器件的性能和成品率有着重要的影响 ,因此需要对薄膜质量进行必要的检查 ,厚度 测量是薄膜质量检查的重要内容之一3 .干涉法测量薄膜厚度是实验和生产中较普遍采用的测量方法 ,其优点是设备简单 ,操作方便 ,无需复杂 的计算. 除了常规的空气膜劈尖干涉法外4 ,本文就等厚干涉法的另外两种形式测量薄膜厚度的原理分别 进行了探讨.空气劈尖取一小片硅片部分地覆盖衬底 , 放入反应腔内生长薄膜 , 生长完成后取下硅片即形成台阶. 将薄玻璃片与带有薄膜台阶的样品沿平行于台阶方向对合 , 一端轻轻压紧 , 另一端用纸片分隔 , 形成空气劈尖 ( 如图 1 所示) . 在读数显微镜下便可观察到干涉条纹. 衬底的一半沉积有厚度为 D 的不透明薄膜 , 它改变了空气膜的厚度 , 即改变了光程差 , 从而使直条纹发生弯折[ 5 ]. 为形成条纹的突然弯折 , 薄膜台阶应尽量陡直.第 k 级暗纹位置 e k 由 ( 1) 式确定 ,1 λλ δ = 2 e k += ( 2 k + 1)暗纹k = 0 , 1 , 2 , 3( 1)22干涉条纹为平行于劈尖棱边的直线条纹 , 每一条纹与空气劈尖的一定厚度 e k 对应. 任意两相邻的暗条纹之间的距离 l 由 ( 2) 式决定 ,λ 1 1l s in θ = e k = 2( k + 1)λ - 2k λ = e k +1 - ( 2) 2式中θ为劈尖的夹角. 可见 , 干涉条纹是等间距的 , 而且θ越小 , l 越大 , 即干涉条纹愈疏 , 反之亦然. 沉积了薄膜的一侧的第 k 级暗纹位置 e ′由( 3) 式确定 λ λ 2 e ′k + = ( 2 k + 1)( 3) 2条纹移动的距离 a 满足a sin θ = e ′k - e k = D结合( 2) 、( 4) 两式可以得到 2( 4)λ a D = ·l( 5)2收稿日期 :2011 - 08 - 15基金项目 :国家自然科学基金( 61106011) 作者简介 :左则文( 1978 - ) , 男 , 安徽郎溪人 , 讲师 , 博士 , 主要从事硅基低维材料与器件方面的研究.透明薄膜劈尖很多薄膜材料在可见光范围内是透明的. 这 里 ,我们以 SiO 2 为例来阐述另一种等厚干涉法测 量透明薄膜厚度的原理.在单晶硅( Si ) 衬底上用化学气相沉积的方法 沉积一层 SiO 2 ,切取一小片用于厚度测量. 将待测 样品切面沿某一方向 ( 以一定角度) 轻磨即可形成 如图 2 所示的 SiO 2 劈尖.2 图 1 弯折干涉条纹示意图Figure 1 Schematic diagram of kinked 2f ringes当用单色光垂直照射 SiO 表面时 , 由于 SiO 2 2 是透明介质 ,入射光将分别在 SiO 2 表面和 SiO 22Si界面处反射 ,反射光相干叠加产生干涉条纹. 由于整个 SiO 2 台阶的厚度是连续变化的 ,因此 ,在 SiO 2 台阶上 将出现明暗相间的干涉条纹.在此系统中 ,空气 、SiO 2 、Si 的折射率分别为 1 ,1 . 5 和 3 . 5 ,因此在两个界面上的反射光都存在“半波损失”,其作用相互抵消 ,对光程差不产生影响 ,由此δ = 2 n e k = k λ 明纹k = 0 , 1 , 2 , 3 ( 5)λ δ = 2 ne k = ( 2 k + 1)暗纹k = 0 , 1 , 2 , 32式中 n 为 SiO 2 的折射率 , e k 为条纹处 SiO 2 层的厚度. 在 SiO 2 台阶楔尖处 e k = 0 , 所以为亮条纹.由 ( 5) 式 , 可以得到两相邻明纹之间的 SiO 2 层的厚度差为( k + 1) λ k λ λ ( 6)e k +1 - e k =- 2 n = 2 n2 n 同样 , 两相邻暗纹之间的 SiO 2 层的厚度差也 为 λ . 2 n由此可见 , 如果从 SiO 2 台阶楔尖算起至台阶顶端共有 m + 1 个亮条纹 ( 或暗条纹) , 则 SiO 2 层的厚度应为λ m2 n( 7)D = 图 2 SiO 2 劈尖形成的干涉示意图Schematic diagram of int erference o n SiO 2 wedge因此 , 已知 SiO 2 的折射率 n ( ≈ 1 . 5 , 与生长条Figure 2 件有关) , 通过读数显微镜观察条纹数即可由( 7) 式得到透明薄膜的厚度. 实验结果与分析以单晶硅作为衬底 ,采用化学气相沉积的方法生长非晶硅薄膜 ,沉积过程中用小片硅片部分遮盖以形成台阶. 作为参考 ,首先用扫描电子显微镜( SE M ) 对 其剖面进行测量 ,得到薄膜的厚度约为 755 n m. 再用 空气劈尖法对薄膜的厚度进行测量 ,得到如下的数据 :3l ( mm )a ( mm )D ( nm )1 230 . 135 0 . 136 0 . 1340 . 353 0 . 352 0 . 354770 . 455 762 . 624 778 . 404实验所用钠双线的波长为分别为 589 . 0 n m 和 589 . 6 nm ,取其平均值 589 . 3 nm 作为入射波长. 计算得到的薄膜平均厚度为 770 . 5 nm ,与扫描电子显微镜测量的结果非常接近 ,表明空气劈尖法可以比较精确地测量薄膜的厚度.利用化学气相沉积法在硅片上生长 SiO 2 薄膜 ,并采用如前所述的方法形成 SiO 2 的劈尖 ,并用读数显微 镜测量劈尖上的干涉条纹. 读数显微镜观察到 SiO 2 劈尖上共有 5 条完整的亮纹 ,即 m = 4 . 取 SiO 2 的折射率为 1 . 5 ,利用公式 ( 7) 计算得到薄膜的厚度约为 785 . 7 n m ,而用扫描电子显微镜测量的剖面厚度约为 853参考文献 :周之斌 ,张亚增 ,张立昆 ,杜先智. 光电器件用铟锡氧化物 I T O 薄膜的制备及特性研究J . 安徽师范大学学报 :自然科学版 ,1995 ,18 ( 2) :66 - 69 . 万新军 ,褚道葆 ,陈声培 ,黄桃 ,侯晓雯 ,孙世刚. 不锈钢表面修饰纳米合金膜电极的电催化活性研究J . 安徽师范大学学报 : 自然科学版 , 2007 ,30 ( 5) :567 - 569 .高雁. 真空蒸发镀膜膜厚的测量J . 大学物理实验 ,2008 ,21 ( 4) :17 - 19 .方正华. 大学物理实验教程M . 合肥 :中国科学技术大学出版社 ,2010 :123 - 129 . 单慧波. 牛顿环实验的拓展J . 物理实验 ,1996 ,16 ( 6) :290 .1 2 3 4 5Two Methods f or Mea s uring the Thickness of Fil m s B a s ed on EqualThickness I nterf e renceZU O Ze 2wen( College of Physics and Elect ro nics Inf o r matio n , Anhui No r m al U niversit y , Wuhu 241000 , China )Abstract : Equal t h ickness interference met h o d is widely applied in p r o d ucti o n due to it s sim ple equip m ent ,co nvenient operati o n , and unco m plicated analysis p rocess. In t his paper , t he p rinciple of t wo met ho d s fo rmeasuring t he t hickness of films based o n equal t hickness interference was discussed. In t hese met ho d s ,m o nochro matic light ref lect s at top and bot to m interf aces of t he wedge 2shaped air o r t ransparent material f ilm s ,w hich is fo r med by utilizing t he step of films , and fo r ms t he interference f ringes. By measuring t he parameters of f ringes , t he t hickness of t he film can be o btained. C o m pared to film 2wedged met ho d , air 2wedged met h o d ism o re appliable due to it s sim pleness and p r ecisi o n .K ey w ords : equal t h ickness interference ; films ; measurement of t h e t h ickness。

椭偏仪测量薄膜厚度和折射率实验报告实验目的：1.学习使用椭偏仪测量薄膜的厚度和折射率。

2.了解光线在薄膜中的传播和干涉现象。

实验仪器和材料：1.椭偏仪2.微米螺旋3.干净的玻璃片4.一块薄膜样品5.直尺6.实验台7.光源实验原理：椭偏仪是一种用于测量透明物体表面薄膜的厚度和折射率的仪器。

当光线从真空进入具有一定折射率的介质中时，会发生折射和反射。

当光线垂直入射到薄膜表面时，经过多次反射和折射后会形成干涉现象。

通过观察测量光的振幅和相位差的变化，可以推导出薄膜的厚度和折射率。

实验步骤：1.将实验台安装好，并确保椭偏仪的光源正常工作。

2.用直尺测量玻璃片和薄膜样品的尺寸，并记录下来。

3.将玻璃片放在实验台上，并将椭偏仪对准玻璃片。

4.调节椭偏仪的干涉仪臂使得产生清晰的干涉条纹。

5.使用微米螺旋逐渐调整反射镜的角度，直到条纹的清晰度达到最佳状态。

6.记录下此时的微米螺旋读数，并用直尺测量薄膜样品的厚度，得到薄膜的实际厚度。

7.调节椭偏仪的角度，使得干涉条纹平行于椭偏仪的刻度线。

8.记录下此时的椭偏仪读数，并计算出薄膜的厚度。

9.重复以上步骤2-8三次，并求取平均值。

10.使用已知的材料的折射率标定椭偏仪，并根据标定值计算出薄膜样品的折射率。

实验结果：根据实验步骤中记录的数据，计算出薄膜样品的平均厚度和折射率。

实验讨论：2.在实验中，可以尝试调节椭偏仪的角度和干涉条纹的清晰度，以获得更准确的测量结果。

3.实验中使用的薄膜样品的厚度和折射率可以进一步研究其与其他因素的关系，如温度、湿度等。

实验结论：通过使用椭偏仪测量薄膜的厚度和折射率，可以得到薄膜样品的相关参数。

实验结果表明，椭偏仪是一种能够精确测量薄膜和折射率的有效工具。

通过该实验，我们可以深入理解光的干涉现象和薄膜的光学性质。

牛顿环实验的应用测量透明薄膜的厚度牛顿环实验是一种基于光的干涉现象的实验，广泛用于测量透明薄膜的厚度。

通过分析干涉图案中的环的半径，我们可以计算出薄膜的厚度。

本文将详细介绍牛顿环实验的原理和应用。

一、实验原理牛顿环实验基于光的干涉原理，利用光波在透明薄膜表面反射和折射时的相位差来形成干涉图样。

在光波垂直入射透明薄膜表面时，光波会发生部分反射和部分折射。

这两束光线在空气和薄膜之间形成一定的干涉现象。

二、实验步骤1. 准备实验所需材料和仪器，包括光源、透明薄膜样品、凸透镜、目镜、平台等。

2. 将透明薄膜样品放置在平台上，调整样品的平整度和水平度。

3. 将凸透镜放置在透明薄膜样品上方一定的距离处。

4. 使用光源照射透明薄膜样品，观察干涉图样。

5. 调整凸透镜和目镜的位置，使得目镜对准干涉图样的中心。

此时，目镜所在位置的高度差即为牛顿环的半径。

6. 根据牛顿环实验的公式计算出透明薄膜的厚度。

三、应用优势1. 测量精度高：牛顿环实验可以通过精确计算环的半径来得到薄膜的厚度，测量精度较高，适用于对薄膜厚度有较高要求的应用场景。

2. 非破坏性测量：牛顿环实验不需要对样品进行破坏性处理，能够保持样品完整性和原始性质，对透明薄膜进行非破坏性测量。

3. 快速测量：牛顿环实验只需较短的时间即可完成测量，便于快速获得薄膜厚度信息。

4. 应用领域广泛：牛顿环实验在许多领域都有广泛应用，如光学器件制造、材料科学研究、光学薄膜的质量控制等。

四、实验数据分析通过牛顿环实验测量得到的环半径，结合实验中的相关参数，可以利用公式计算出透明薄膜的厚度。

在数据分析过程中，需要考虑各种误差来源，并采取相应的措施进行校正。

五、实验注意事项1. 实验环境要求较高，需要在光线较暗的条件下进行，以确保干涉图样的清晰度。

2. 在放置透明薄膜样品时，要注意保持其平整度和水平度，以避免引入额外的误差。

3. 使用凸透镜和目镜时，要小心调整其位置，以确保目镜与干涉图样中心的准确对准。

薄膜厚度测试方法薄膜厚度测试方法薄膜是一种非常薄的材料，广泛应用于电子产品、光学设备、食品包装等各个领域。

薄膜的厚度是决定其性能和功能的重要指标之一。

因此，准确测量薄膜厚度对于生产和研发过程至关重要。

下面将介绍一些常见的薄膜厚度测试方法。

1. 光学显微镜法：这是一种简单直观的测量方法。

通过光学显微镜观察薄膜的表面形貌，再利用光学原理计算出厚度。

这种方法适用于较厚的透明薄膜。

但是，由于光学显微镜的分辨率限制，对于较薄的薄膜可能无法得到准确的结果。

2. 非接触式光学测厚仪法：这种方法利用光学干涉原理测量薄膜的厚度。

其基本原理是通过两束光的干涉现象来计算薄膜的厚度。

该方法在测量过程中不接触样品，不会对薄膜造成破坏，适用于薄膜材料的在线测量。

3. 厚度计法：使用厚度计是一种常见且简便的方法。

通过将薄膜放置在厚度计上，利用压力或力传感器测量薄膜下方的厚度，从而得到薄膜厚度的数据。

这种方法适用于较厚的薄膜，但对于较薄的薄膜可能会存在测量误差。

4. 散射光测量法：这种方法利用光的散射现象来测量薄膜的厚度。

通过照射薄膜并测量散射光的强度和角度，可以计算出薄膜的厚度。

这种方法适用于透明的薄膜。

5. X射线荧光光谱法：这是一种利用X射线的方法来测量薄膜厚度的技术。

通过照射薄膜样品，观察其所产生的特定荧光，再根据荧光的特性来计算薄膜的厚度。

这种方法适用于一些特殊材料的测量。

综上所述，薄膜厚度的测量方法多种多样，我们需要根据实际情况选择合适的方法。

在选择之前，我们需要考虑薄膜的材料特性、厚度范围和对测量精度的要求。

合理选择和应用薄膜厚度测试方法，不仅有助于确保产品质量，还能提高生产效率，降低成本，推动科学研究的进展。

椭偏法测薄膜厚度实验报告椭偏法测薄膜厚度实验报告引言：薄膜厚度的测量在材料科学和工程领域具有重要的意义。

传统的测量方法往往需要破坏性测试或者复杂的设备，而椭偏法则提供了一种非接触、快速、准确的测量手段。

本实验旨在利用椭偏法测量薄膜的厚度，并探究其原理和应用。

实验方法：1. 实验材料准备：本实验使用了一块透明的玻璃基板和一层薄膜样品。

玻璃基板的折射率已知，而薄膜的厚度需要测量。

为了减少误差，实验前需确保样品表面无杂质和污染。

2. 椭偏仪器设置：将椭偏仪器与计算机连接，并进行校准。

校准过程中需要调整仪器的角度、光源强度和偏振片的角度，以确保测量的准确性。

3. 测量过程：将样品放置在椭偏仪器的样品台上，并调整样品位置，使其与光线垂直。

然后，通过椭偏仪器发送的光线照射到样品上，并通过光电探测器接收反射光。

仪器会自动记录光电探测器接收到的信号，并根据信号的变化计算出薄膜的厚度。

实验结果：根据实验数据的分析，我们得到了薄膜的厚度。

通过椭偏法的测量结果，我们可以得出以下结论：1. 椭偏法的优势：椭偏法作为一种非接触、快速、准确的测量手段，具有以下优势：- 非接触性：椭偏法不需要直接接触样品，避免了对样品的破坏。

- 快速性：椭偏法可以在短时间内完成测量，提高了工作效率。

- 准确性：椭偏法基于光学原理，具有较高的测量精度和可靠性。

2. 实验误差分析：在实验过程中，可能会存在一些误差，包括但不限于以下因素：- 光源的稳定性：光源的稳定性会影响到测量结果的准确性，因此需要选择稳定的光源。

- 样品表面的污染：样品表面的污染会影响到光的入射和反射，从而导致测量误差。

- 仪器的校准：仪器的校准对于测量结果的准确性至关重要，需要进行仔细的校准。

实验应用：椭偏法广泛应用于薄膜领域的研究和生产中。

其应用包括但不限于以下方面：1. 薄膜厚度测量：椭偏法可以用于测量各种材料的薄膜厚度，例如金属薄膜、氧化物薄膜等。

通过测量薄膜的厚度，可以评估材料的性能和质量。

pmma薄膜厚度PMMA薄膜厚度PMMA（聚甲基丙烯酸甲酯）是一种常见的透明塑料材料，具有优良的光学性能和机械性能，在各个领域有广泛的应用。

薄膜是PMMA材料的一种常见形式，其厚度对其性能和应用起着重要的影响。

一、PMMA薄膜的制备方法制备PMMA薄膜的方法有多种，常见的有溶液浇铸法、拉伸法和溶液吸附法等。

其中，溶液浇铸法是最常用的方法之一。

该方法是将PMMA溶液倒在平整的基底上，通过溶剂的挥发使PMMA形成薄膜。

溶液的浓度和浇铸速度等因素会影响薄膜的厚度。

二、PMMA薄膜的厚度测量方法测量PMMA薄膜厚度的常用方法有光学显微镜法、原子力显微镜法和厚度计等。

光学显微镜法是一种简单直观的方法，通过显微镜观察薄膜的厚度。

原子力显微镜法则是利用原子力显微镜的探针扫描薄膜表面，通过探针的运动轨迹来计算薄膜的厚度。

而厚度计则是利用电磁波的传播特性来测量薄膜的厚度。

三、PMMA薄膜厚度的影响因素PMMA薄膜的厚度对其性能和应用起着重要的影响。

首先，薄膜的厚度会影响其光学性能，如透光率和折射率等。

一般来说，较薄的PMMA薄膜具有更高的透光率和较低的折射率。

其次，薄膜的厚度还会影响其机械性能，如强度和韧性等。

一般来说，较厚的PMMA 薄膜具有较高的强度和较低的韧性。

此外，薄膜的厚度还会影响其表面形态和粗糙度，对于特定的应用来说，薄膜的平整度和光滑度也是重要考虑因素。

四、PMMA薄膜的应用领域PMMA薄膜由于其优良的光学性能和机械性能，在各个领域有广泛的应用。

在光学领域，PMMA薄膜可用于制作光学元件，如透镜和滤光片等。

在电子领域，PMMA薄膜可用于制作显示屏的保护膜和触摸屏的感应层等。

在建筑领域，PMMA薄膜可用于制作采光板和隔音板等。

此外，PMMA薄膜还可用于制作装饰材料、包装材料和光纤等。

PMMA薄膜的厚度对其性能和应用起着重要的影响。

通过不同的制备方法和测量方法，可以获得不同厚度的PMMA薄膜。

薄膜的厚度会影响其光学性能、机械性能和表面形态等特性。

ASTM D2683是美国材料和试验协会（ASTM）制定的用于测量塑料薄膜的厚度的标准方法。

该标准方法适用于透明、不透明或半透明的塑料薄膜。

要按照ASTM D2683标准测量厚度，需要遵循以下步骤：
1. 准备工具和材料：需要使用精确的切割工具、薄膜厚度计（如显微镜、薄膜厚度计等）和待测的塑料薄膜样品。

2. 制备样品：使用精确的切割工具将薄膜切割成适当大小的样品。

样品的尺寸和形状应符合标准要求。

3. 安装样品：将样品放置在薄膜厚度计的测量位置上，确保其与测量仪器的接触平整。

4. 调整仪器：将薄膜厚度计调整至合适的工作状态，确保其测量精度和稳定性。

5. 测量厚度：按照薄膜厚度计的操作指南，对样品的各个位置进行多次测量，并记录测量结果。

6. 处理数据：对测量结果进行统计和处理，计算平均厚度、标准偏差等参数。

7. 遵守标准：在测量过程中遵守ASTM D2683标准的要求，确保测量结果的准确性和可靠性。

需要注意的是，ASTM D2683标准是针对塑料薄膜的厚度测量，对于其他类型的材料或应用场景，可能需要使用其他相应的标准和测量方法。

测量薄膜厚度的方法测量薄膜厚度是一项重要的技术任务，它在很多领域都有广泛的应用，如材料科学、纳米科技、光学等。

本文将介绍几种常见的测量薄膜厚度的方法。

一、光学干涉法光学干涉法是一种基于干涉现象的测量方法。

当光线从空气射入不同折射率的介质中时，会发生反射和透射。

薄膜的厚度决定了光线的相位差，通过测量干涉条纹的变化，可以计算出薄膜的厚度。

这种方法适用于透明薄膜的测量，如薄膜涂层厚度的测量。

二、原子力显微镜（AFM）原子力显微镜是一种利用探针与样品表面之间的相互作用力来进行测量的仪器。

通过探针在样品表面扫描，可以获取样品表面的拓扑图像，并结合探针与样品之间的力信号，可以计算出薄膜的厚度。

AFM具有高分辨率和高灵敏度的优点，适用于测量纳米薄膜的厚度。

三、X射线衍射法X射线衍射法是一种基于X射线与物质相互作用的测量方法。

X射线经过物质时会发生衍射，不同厚度的薄膜会产生不同的衍射图样。

通过测量衍射图样的特征参数，可以计算出薄膜的厚度。

这种方法适用于非透明薄膜的测量，如金属薄膜的厚度测量。

四、椭偏仪法椭偏仪法是一种基于光的偏振现象的测量方法。

当偏振光通过薄膜时，会发生偏振状态的改变，通过测量偏振光的参数变化，可以计算出薄膜的厚度。

这种方法适用于透明薄膜的测量，如液晶显示器中薄膜的厚度测量。

五、电子显微镜法电子显微镜法是一种利用电子束与物质相互作用的测量方法。

电子束经过薄膜时会发生散射，通过测量散射电子的特征参数，可以计算出薄膜的厚度。

电子显微镜法具有高分辨率和高灵敏度的特点，适用于测量纳米薄膜的厚度。

测量薄膜厚度的方法有很多种，每种方法都有其适用的范围和特点。

在实际应用中，可以根据具体情况选择合适的方法进行测量。

同时，随着科技的不断发展，还会有更多新的测量方法出现，为薄膜厚度的测量提供更多选择和便利。