测量薄膜厚度及其折射率的方法PPT
- 格式:ppt
- 大小:266.50 KB
- 文档页数:16
镀个较厚一点的单层膜,根据极值点(膜比基底折射率高的看极小值,膜比基底折射率低的看极大值,并且选取长波段的极值点,因为在长波段折射率色散小)估算出膜层的折射率,该点的反射率,根据薄膜光学原理,相当于单个四分之一光学厚度的膜厚(单层四分之一光学厚度的薄膜等效折射率为n^2/ng,n为膜的折射率,ng为基底折射率)的反射率。
算出折射率后,再判断极值级次,根据这个级次就可算出膜厚。
现在举一例子加深理解。
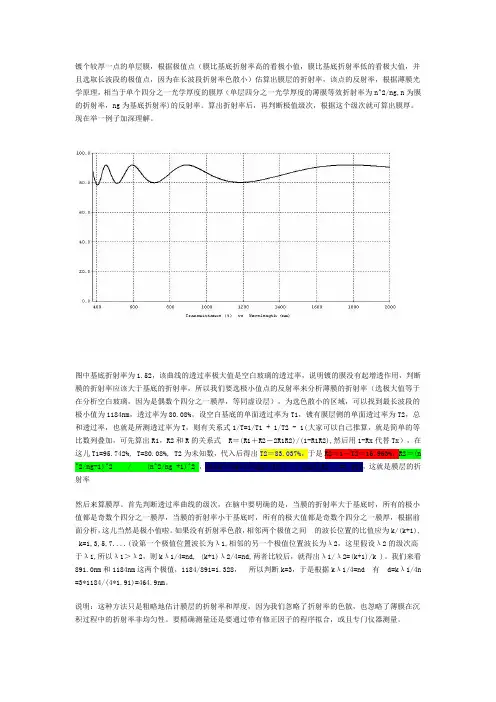
图中基底折射率为1.52,该曲线的透过率极大值是空白玻璃的透过率,说明镀的膜没有起增透作用,判断膜的折射率应该大于基底的折射率,所以我们要选极小值点的反射率来分析薄膜的折射率(选极大值等于在分析空白玻璃,因为是偶数个四分之一膜厚,等同虚设层),为选色散小的区域,可以找到最长波段的极小值为1184nm,透过率为80.08%。
设空白基底的单面透过率为T1,镀有膜层侧的单面透过率为T2,总和透过率,也就是所测透过率为T,则有关系式1/T=1/T1 + 1/T2 - 1(大家可以自己推算,就是简单的等比数列叠加,可先算出R1,R2和R的关系式R=(R1+R2-2R1R2)/(1-R1R2),然后用1-Rx代替Tx),在这儿T1=95.742%, T=80.08%, T2为未知数,代入后得出T2=83.037%,于是R2=1-T2=16.963%,R2=(n ^2/ng-1)^2 / (n^2/ng +1)^2 ,n=sqrt(ng*(1+sqrt(R2))/(1-sqrt(R2) )=1.910,这就是膜层的折射率然后来算膜厚。
首先判断透过率曲线的级次,在脑中要明确的是,当膜的折射率大于基底时,所有的极小值都是奇数个四分之一膜厚,当膜的折射率小于基底时,所有的极大值都是奇数个四分之一膜厚,根据前面分析,这儿当然是极小值啦。
如果没有折射率色散,相邻两个极值之间的波长位置的比值应为k/(k+1), k=1,3,5,7....(设第一个极值位置波长为λ1,相邻的另一个极值位置波长为λ2,这里假设λ2的级次高于λ1,所以λ1>λ2,则kλ1/4=nd, (k+1)λ2/4=nd,两者比较后,就得出λ1/λ2=(k+1)/k )。




椭偏光法测量薄膜的厚度和折射率1. 实验目的(1) 了解椭偏光法测量原理和实验方法; (2) 熟悉椭偏仪器的结构和调试方法; (3) 测量介质薄膜样品的厚度和折射率。
2. 实验原理本实验介绍反射型椭偏光测量方法。
其基本原理是用一束椭偏光照射到薄膜样品上,光在介质膜的交界面发生多次的反射和折射,反射光的振幅和位相将发生变化,这些变化与薄膜的厚度和光学参数(折射率、消光系数等)有关,因此,只要测出反射偏振状态的变化,就可以推出膜厚度和折射率等。
2.1 椭圆偏振方程图1所示为均匀、各向同性的薄膜系统,它有两个平行的界面。
介质1为折射率为n 1的空气,介质2为一层厚度为d 的复折射率为n 2的薄膜,它均匀地附在复折射率为n 3的衬底材料上。
φ1为光的入射角,φ2和φ3分别为薄膜中和衬底中的折射角。
光波的电场矢量可分解为平行于入射面的电场分量(p 波)和垂直于入射面的电场分量(s 波)。
用(I p )i 和(I s )i 分别代表入射光的p 分量和s 分量,用(I p )r 和(I s )r 分别代表各反射光O p ,I p ,II p ···中电矢量的p 分量之和及各束反射光s 分量之和。
定义反射率(反射系数)r 为反射光电矢量的振幅与入射光电矢量的振幅之比。
则由菲涅耳公式,有 对空气-薄膜界面I :r 1p =n 2cosφ1−n 1cosφ2n 2cosφ1+n 1cosφ2(1)r 1s =n 1cosφ1−n 2cosφ2n 1cosφ1+n 2cosφ2(2)对薄膜-衬底界面II :r 2p =n 3cosφ2−n 2cosφ3n 3cosφ2+n 2cosφ3(3)r 2s =n 2cosφ2−n 3cosφ3n 2cosφ2+n 3cosφ3图1 薄膜系统的光路示意图I pO pI pII p根据折射定律,有n1sinφ1=n2sinφ2=n3sinφ3(5) 由图1,可算出任意两相邻反射光之间的光程差为l=2n2dcosφ2相应的相位差为2δ=360°λl于是可得δ=360°λd(n22−n12sin2φ1)12⁄(6)另一方面,由多束光干涉原理来考察空气-薄膜-衬底作为一个整体系统的总反射系数,以R p 和R s分别表示这个系统对p波和s波的总反射系数,则由图1可知,对p波,R p由O p,I p,II p···各级反射光叠加合成。



椭圆偏振光法测量薄膜的厚度和折射率摘要:本实验中,我们用椭圆偏振光法测量了MgF 2,ZrO 2,TiO 2三种介质膜的厚度和折射率,取MgF 2作为代表,测量薄膜折射率和厚度沿径向分布的不均匀性,此外还测量了Au 和Cr 两种金属厚膜的折射率和消光系数。
掌握了椭圆偏振光法的基本原理和技术方法。
关键词:椭偏法,折射率,厚度,消光系数 引言:薄膜的厚度和折射率是薄膜光电子器件设计和制备中不可缺少的两个参数。
因此,精确而迅速地测定这两个参数非常重要。
椭圆偏振光法就是一个非常重要的方法。
将一束单色椭圆偏振光投射到薄膜表面,根据电动力学原理,反射光的椭偏状态与薄膜厚度和折射率有关,通过测出椭偏状态的变化,就可以推算出薄膜的厚度和折射率。
椭圆偏振光法是目前测量透明薄膜厚度和折射率时的常用方法,其测量精度高,特别是在测量超薄薄膜的厚度时其灵敏度很高,因此常用于研究薄膜生长的初始阶段,而且由于这种方法时非接触性的,测量过程中不破坏样品表面,因而可用于薄膜生长过程的实时监控。
本实验的目的是掌握椭偏法测量薄膜的厚度和折射率的原理和技术方法。
测量几种常用介质膜的折射率和厚度,以及金属厚膜的复折射率。
原理:1. 单层介质膜的厚度和折射率的测量原理(1)光波在两种介质分界面上的反射和折射,有菲涅耳公式:121122112112211122322323223223322233cos cos cos cos cos cos cos cos cos cos cos cos cos cos cos cos p s p s n n r n n n n r n n n n r n n n n r n n ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ-⎧=⎪+⎪-⎪=⎪+⎪⎨-⎪=⎪+⎪-⎪=⎪+⎩(tp-1); (2)单层膜的反射系数图1 光波在单层介质膜中传播以上各式中1n 为空气折射率,2n 为膜层的折射率,3n 为衬底折射率。
1ϕ为入射角,2ϕ,3ϕ分别为光波在薄膜和衬底的折射角。

⽤椭偏仪测薄膜厚度与折射率103实验⼗⼆⽤椭偏仪测薄膜厚度与折射率随着半导体和⼤规模集成电路⼯艺的飞速发展,薄膜技术的应⽤也越加⼴泛。
因此,精确地测量薄膜厚度与其光学常数就是⼀种重要的物理测量技术。
⽬前测量薄膜厚度的⽅法很多。
如称重法、⽐⾊法、⼲涉法、椭圆偏振法等。
其中,椭圆偏振法成为主要的测试⼿段,⼴泛地应⽤在光学、材料、⽣物、医学等各个领域。
⽽测量薄膜材料的厚度、折射率和消光系数是椭圆偏振法最基本,也是⾮常重要的应⽤之⼀。
实验原理由于薄膜的光学参量强烈地依赖于制备⽅法的⼯艺条件,并表现出明显的离散性,因此,如何准确、快速测量给定样品的光学参量⼀直是薄膜研究中⼀个重要的问题。
椭圆偏振法由于⽆须测定光强的绝对值,因⽽具有较⾼的精度和灵敏度,⽽且测试⽅便,对样品⽆损伤,所以在光学薄膜和薄膜材料研究中受到极⼤的关注。
椭圆偏振法是利⽤椭圆偏振光⼊射到样品表⾯,观察反射光的偏振状态(振幅和位相)的变化,进⽽得出样品表⾯膜的厚度及折射率。
氦氖激光器发出激光束波长为632.8nm 的单⾊⾃然光,经平⾏光管变成单⾊平⾏光束,再经起偏器P 变成线偏振光,其振动⽅向由起偏器⽅位⾓决定,转动起偏器,可以改变线偏振光的振动⽅向,线偏振光经1/4波⽚后,由于双折射现象,寻常光和⾮寻常光产⽣π/2的位相差,两者的振动⽅向相互垂直,变为椭圆偏振光,其长、短轴沿着1/4波⽚的快、慢轴。
椭圆的形状由起偏器的⽅位⾓来决定。
椭圆偏振光以⼀定的⾓度⼊射到样品的表⾯,反射后偏振状态发⽣改变,⼀般仍为椭圆偏振光,但椭圆的⽅位和形状改变了。
从物理光学原理可以知道,这种改变与样品表⾯膜层厚度及其光学常数有关。
因⽽可以根据反射光的特性来确定膜层的厚度和折射率。
图1为基本原理光路。
图2为⼊射光由环境媒质⼊射到单层薄膜上,并在环境媒质——薄膜——衬底的两个界⾯上发⽣多次折射和反射。
此时,折射⾓满⾜菲涅尔折射定律332211sin sin sin N N N ==(1)104 其中N 1,N 2和N 3分别是环境媒质、= n – i k );?1为⼊射⾓、 ?2 和?3分别为薄膜和衬底的折射⾓。

