高中数学知识网络图

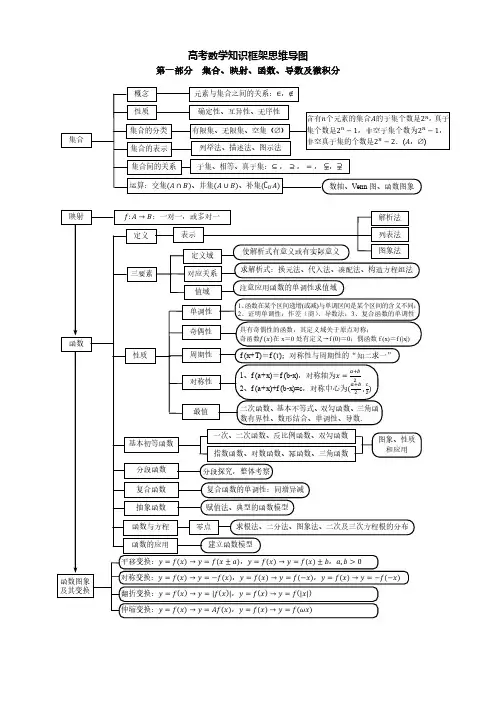
;;=⇔⊆=⇔⊆=⇔⊆A B B A B A B A A B A B I A Bn-个A中元素有n个，则A的子集共有2n个，真子集有21集合间的运算2n R a +∈则2n n a n a ++≥平均值不等式2nnn a a n++≥当且仅当2,,)n 时取等号1111221n j n j n n n a b a b a b a b a b a b ++≤++≤+++,n Z 是∀,,nx 是区间1122)()()()n n n n q x q f x q f x q f x ++≤+++,,,1n i q R q +∈=∑）。

上凸函数不等号转向.1}n ma+仍是等比数列，其公比为)lim n n a ++=sin sin αtan tan 1tan tan α±2(AB x =，则a ⊥b2PP 所成比112222221cos ||||a b a b a ba b a b a ++⋅⋅==⋅+212()(x x y y =-+-空间向量的直角坐标运算律若123(,,a a a a =，12(,,b b b b =则①113(a b a b +=+，11(a b a b -=-123(,)()a a a R λλλλλ=∈，11a b a b ⋅=+②13//a ba b λλ⇔=，110a b a b ⊥⇔+若111(,,)A x y z 则2(AB x =-模长公式若12(,,a a a a =21||a a a a a =⋅=+空间向量的运算,,(OB OA AB a b BA OA OB a b OP a λλ=+=+=-=-=空间向量的加减与数乘OB OA AB =+=a +b ，AB OB OA =-，,(OP λ=a a b + c ⑶数乘分配律：λ(a + ) =λa +λb ．平行六面体向量的数乘积||||cos ,a b a b a b ⋅=⋅⋅<>空间向量数乘积的性质①||cos ,a e a a e ⋅=<>．②0a b a b ⊥⇔⋅=．③2||a a a =⋅．空间向量数量积运算律①()()()a b a b a b λλλ⋅=⋅=⋅②a b b a ⋅=⋅（交换律） ③()a b c a b a c ⋅+=⋅+⋅（分配律）④e a = a e =|a |cos ,a e⑤ab a b = 0⑥当a 与b 同向时，a b = |a ||b |；当a 与b 反向时，a b = |a ||b |.特别的a a = |a |2或||a a a =⋅⑦cos ,||||a ba b a b ⋅=Bα∈，则l αβ=且l，则A、B、C 。

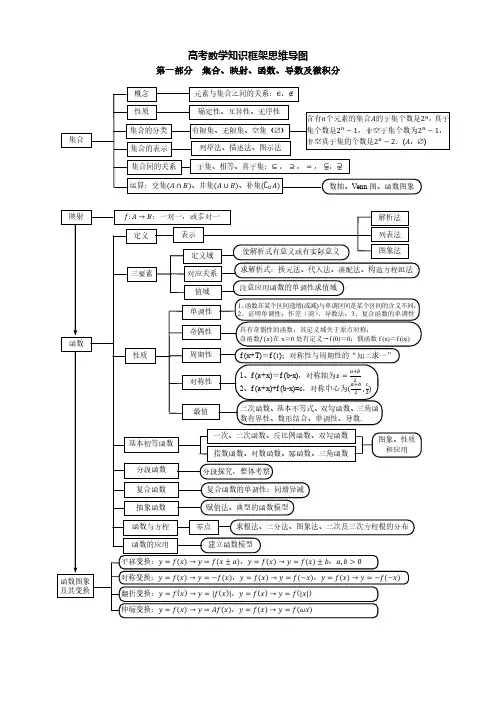
高一数学第二张知识点框架图高一数学第二章知识点框架图高一数学的第二章主要涉及到函数的基本概念、性质与图像以及反函数的相关内容。

下面将以框架图的形式进行论述。

一、函数的基本概念1. 函数的定义函数是一种特殊的关系，每个自变量x都对应唯一的因变量y。

2. 函数的表示方法（1）显式表示法：y = f(x)，其中f(x)表示函数关系。

（2）隐式表示法：F(x, y) = 0，其中F(x, y)表示函数关系。

二、函数的性质与图像1. 定义域和值域（1）定义域：自变量x的取值范围。

（2）值域：因变量y的取值范围。

2. 奇偶性与周期性（1）奇函数：f(-x) = -f(x)，图像关于原点对称或关于原点旋转180°对称。

（2）偶函数：f(-x) = f(x)，图像关于y轴对称或关于原点旋转360°对称。

（3）周期函数：f(x + T) = f(x)，其中T为正常数，图像在区间[a, a + T]内完全相同。

3. 单调性与极值（1）单调增函数：f(x1) < f(x2)（x1 < x2），图像从左向右递增。

（2）单调减函数：f(x1) > f(x2)（x1 < x2），图像从左向右递减。

（3）极大值：f(x)在某段区间上的值大于或等于该区间内任意其他点的函数值。

（4）极小值：f(x)在某段区间上的值小于或等于该区间内任意其他点的函数值。

三、反函数1. 反函数的定义若函数f的值域为Y，对于Y中的任一元素y，若存在唯一的x使得f(x) = y，则称x是函数f的反函数g的值，记作g(y) = x。

2. 图像与性质（1）函数与反函数的图像关于直线y = x对称。

（2）若函数f在[a, b]上单调递增（或递减），则其反函数在[f(a), f(b)]上单调递增（或递减）。

总结：高一数学的第二章主要介绍了函数的基本概念、性质与图像以及反函数的相关内容。

在函数的基本概念部分，我们了解到函数是一种特殊的关系，每个自变量对应唯一的因变量；函数可以用显式表示法或隐式表示法来表示。

高一数学必修1知识网络集合123412n x A x B A B A B A n A ∈∉⎧⎪⎪⎨⎪⎪⎩∈⇒∈⊆（）元素与集合的关系：属于（）和不属于（）（）集合中元素的特性：确定性、互异性、无序性集合与元素（）集合的分类：按集合中元素的个数多少分为：有限集、无限集、空集（）集合的表示方法：列举法、描述法（自然语言描述、特征性质描述）、图示法、区间法子集：若 ，则，即是的子集。

、若集合中有个元素，则集合的子集有个， 注关系集合集合与集合{}00(2-1)23,,,,.4/n A A A B C A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B ⎧⎪⎧⎪⎪⎪⊆⎪⎪⎨⎪⊆⊆⊆⎨⎪⎪⎪⎩⎪⎪⊆≠∈∉⎪⊆⊇⇔=⎪⎩⋂=∈∈⋂=⋂∅=∅⋂=⋂⋂⊆真子集有个。

、任何一个集合是它本身的子集，即 、对于集合如果，且那么、空集是任何集合的（真）子集。

真子集：若且（即至少存在但），则是的真子集。

集合相等：且 定义：且交集性质：，，，运算{}{},/()()()-()/()()()()()()U U U U U U U U A A B B A B A B A B x x A x B A A A A A A B B A A B A A B B A B A Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B ⎧⎪⎨⋂⊆⊆⇔⋂⎪⎩⎧⋃=∈∈⎪⎨⋃=⋃∅=⋃=⋃⋃⊇⋃⊇⊆⇔⋃⎪⎩⋃=+⋂=∈∉=⋂=∅⋃==⋂=⋃，定义：或并集性质：，，，，， 定义：且补集性质：，，，， ()()()U U U C A B C A C B ⎧⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⋃=⋂⎪⎪⎩⎩⎩⎩函数,,,A B A x B y f B A B x y x f y y x y →映射定义：设，是两个非空的集合，如果按某一个确定的对应关系，使对于集合中的任意一个元素， 在集合中都有唯一确定的元素与之对应，那么就称对应：为从集合到集合的一个映射传统定义：如果在某变化中有两个变量并且对于在某个范围内的每一个确定的值，定义 按照某个对应关系都有唯一确定的值和它对应。

高中数学几何知识点思维导图1. 平面几何- 点、线、面的基本概念点、线、面的基本概念- 点：没有大小和形状的几何元素。

- 线：由无数点连成的一根直线。

- 面：有无穷多个点组成的平面。

- 角的概念和分类角的概念和分类- 角：由两条射线共享一个端点构成的几何图形。

- 顶点：角的公共端点。

- 分类：锐角、直角、钝角、平角等。

- 三角形的性质三角形的性质- 三角形：由三条线段连接而成的图形。

- 性质：内角和为180度，外角和为360度，等边三角形的三条边相等。

- 四边形的性质四边形的性质- 四边形：由四条线段连接而成的图形。

- 性质：对角线相互平分，平行四边形的对边对应相等。

- 圆的基本概念和性质圆的基本概念和性质- 圆：平面上一组到一个固定点距离相等的点的集合。

- 弧：圆上的一段弯曲的线段。

- 性质：半径相等的圆相似，圆内任意两点间的线段最短。

2. 空间几何- 立体图形的表面积和体积立体图形的表面积和体积- 表面积：立体图形表面的总面积。

- 体积：立体图形所占的空间大小。

- 常见立体图形：球体、圆柱体、正方体等。

- 平行线与平面的关系平行线与平面的关系- 平行线：在同一个平面上永不相交的两条线。

- 平面：空间中没有限制的延伸的面。

- 射影定理和相似三角形射影定理和相似三角形- 射影定理：平行线与平面相交时，对应的线段成比例。

- 相似三角形：对应角相等，对应边成比例的三角形。

- 球体的性质和计算球体的性质和计算- 性质：球体表面积和体积的计算公式。

- 计算：根据给定的半径或体积计算球体的表面积或体积。

3. 向量几何- 向量的定义和运算向量的定义和运算- 向量：有大小和方向的几何量。

- 定义：用起点和终点表示的有向线段。

- 运算：向量的加法、减法和数乘运算。

- 向量的数量积和向量积向量的数量积和向量积- 数量积：两个向量的数量积为它们的模乘积与夹角余弦的乘积。

- 向量积：两个向量的向量积为它们的模乘积与夹角正弦的乘积。