当前位置：文档之家 › 第2章-张量分析(清华大学张量分析-你值得拥有)PPT课件

第2章-张量分析(清华大学张量分析-你值得拥有)PPT课件

  • 格式：pptx
  • 大小：634.43 KB
  • 文档页数：39

下载文档原格式

  / 39

合集下载

张量分析TensorAnalysisppt课件

张量分析TensorAnalysisppt课件

的切线方向。矢量 r 可以取作曲线坐标系的基矢量（协变基矢量）：
xi
gi

r xi

zj xi
ij
注意：对于在曲线坐标系中的每一点，都有三个基 矢量。
ቤተ መጻሕፍቲ ባይዱ
基矢量一般不是单位矢量，彼此也不正交；
基矢量可以有量纲，但一点的三个基矢量的量纲可以不同；
基矢量不是常矢量，它们的大小和方向依赖于它们所在点的坐标。
利用克罗内克符号，上式可写成：
ds2 ijdxidxj
克罗内克符号的一些常用性质：
ijxi xj
x j xi


j i
ijki kj
D) 置换符号
置换符号eijk=eijk定义为:
1
e ijk
e ijk



1
0
当i,j,k是1，2，3的偶置换(123,231,312) 当i,j,k是1，2，3的奇置换(213,132,321) 当i,j,k的任意二个指标相同
i,j,k的这些排列分别叫做循环排列、逆循环排列和非循环排列。
D) 置换符号（续）
置换符号主要可用来展开三阶行列式：
a11 a1 2 a3 1 aa12 a22 a32 a11a22a33a12a23a3 1a13a1 2a32
a13 a23 a33 a11a23a32 a12a1 2a33 a13a1 2a32
量 Ai ，在坐标系yi中有三个分量 Âi ，它们由以下的变换法则相联系；
AˆiyAjxxyij
逆变矢量用上标表示；因此上标也称为逆变指标。
(3) 协变矢量(一阶协变张量)
一个量被称为协变矢量或一阶协变张量，若它在坐标系 xi 中有三个分 量 Ai ，在坐标系yi中有三个分量 Âi ，其变换法则相为；

02张量分析

02张量分析

1.矢量场的旋度 令 a aP 是位置矢量P的矢量值函数，于是 aP 的左旋度 curla 定义为
Tik ek x i
divTk
类似地，二阶张量场 T TP 的右散度 d ivT 定义为
T i Tik ik Tik ,i xi
d ivT T
(2.2.19)
ij
a j xi

ai i ai xi
18

显然
a1 a 2 a3 x1 x 2 x3
(2.3.03)
但在T为对称张量的情况下， divT divT ，现证明如下：
divT
diva d iva
因此，今后我们对于矢量场的左散度和右散度不加区别，统一地记为
16
dQ T dQ Q Q dt dt
由式(1.9.10)知
(2.1.11)
dQ dQ T Q Q dt dt
于是
T
T
(2.1.12)
dQ T dQ T dt Q dt Q
所以
2.1
标量的张量值函数的导数
设 T Tt 是标量t(例如时间)的张量值函数。T对t的导数由下式定义：
dTij dT dT 的分量 给出。 由T的分量的导数 dt dt dt ij de 事实上，因为 Tij e i T e j ，又因 i 0 ，故有 dt dTij d ei T e j dt dt dT ei e j dt dT dt ij
(2.2.09)
f i
于是f的微分可写成

f x i
(2.2.04)
df f P dP f P f dx xi i

清华大学弹性力学冯西桥FXQ-Chapter-02张量共98页PPT

清华大学弹性力学冯西桥FXQ-Chapter-02张量共98页PPT
生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非
10、一个人应该：活泼而守纪律，天 真而不 幼稚， 勇敢而 鲁莽， 倔强而 有原则 ，热情 而不冲 动，乐 观而不 盲目。 ——马 克思
谢谢你的阅读
清华大学弹性力学冯西 桥FXQ-Chapter-02张
量
6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌，集体的声音， 集体的 动作， 集体的 表情， 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律， 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯

【张量分析ppt课件】张量分析课件第二章 矢量代数与矢量分析

【张量分析ppt课件】张量分析课件第二章 矢量代数与矢量分析

（2.1-3）
在矢量的加法和减法运算中定义单位元素为：
o 0 i1 0 i2 0 i3
同时长度为1的矢量称为单位矢量。 应当注意单位矢量元素和单位矢量的区别。
例2 ： 图 2－4 所示具有坐标系的矢空间 V 中 矢量a、 b。试求 2a +1.5b在{o；i1， i2 }中的表示。 a (3 1) i 1 (1 0) i 2 2 i 1 i 2 解：
a b ( ai i i ) (b j i j ) ai b j ij ai bi b a ; a , b V
（2.1-4） （2.1-5）
1 ; i j i i i j ij 0 ; i j
其中δij称为Kronecker符号。 定义矢量积
例6 ：
证明e—δ恒等式： eijk eimn jm kn jn km 证： 由（2.1-12）式有：i j ik e jkiii eijkii
im in emne ie eemn ie
eijkeemn ii ie (i j ik ) (im in ) (eijkii ) (eemnie ) (i j ik ) (im in ) eijkeemn ie (i j ik ) (im in )
X2
x2
x r2 o r1 x1 (a ) X1
x2 i2 x i1 x1 X1
X2
(b )
图2－3
设V的坐标系为{o；i1，i2，i3}，V中矢量的加法和矢量与 数量的标量积按（1.1-3）和（1.1-4）定义，即对x，y ∈ V；α，β ∈F有 x y xi yi
i i i i
( xi yi ) ii

张量分析清华大学张量分析你值得拥有

张量分析清华大学张量分析你值得拥有

g是正实数（右手系）
斜角直线坐标系旳基矢量与矢量分量
➢ 三维空间中旳斜角直线坐标系和基矢量
定义逆变基矢量 g j，满足对偶条件：
g j gi ij (i, j = 1, 2,3)
问题：已知 gi，怎样求 g j ？
※ 根据几何图形直接拟定
由对偶条件可知， g1与 g2 、g3 均正交，所以正交于 g2与 g3所
第1章 矢量与张量
2023年12月12日
张量旳两种体现形式
实体形式
分量形式
几何形式 定义式
代数形式 计算式
概念旳内涵和外 延（定量）
怎样计算？
主要内容
➢ 矢量及其代数运算 ➢ 斜角直线坐标系旳基矢量与矢量分量 ➢ 曲线坐标系及坐标转换关系 ➢ 并矢与并矢式 ➢ 张量旳基本概念 ➢ 张量旳代数运算 ➢ 张量旳矢积
g1 1
g2 x1(cos x2 cos x3i cos x2 sin x3 j sin x2k) g2 x1
g3 x1注sin:x2(()s式in 只x3i对 c正os交x3曲j) 线坐标系成立，g3 x1 sin x2
☆正交曲可作线为坐求标正系交与系L中am度é量常张数量旳一种措施。
y
※平面极坐标系
(x, y) (x1, x2)
r
g gr
(r, ) (x1, x2 )
矢径：
r x1i x2 j
j
x1
x2
(x1)2 (x2)2
arctan
x2 x1
x1
x1
cos
x2
x2 x1 sin x2
i
x
平面极坐标系
xi' = xi' xi
r g1 i cos x2 j sin x2

第二章 张量(清华大学弹塑性力学)

第二章 张量(清华大学弹塑性力学)
利用爱因斯坦求和约定，写成：
xi aij x j
其中 j 是哑指标，i 是自由指标。
19
Appendix A.1
张量基本概念
★ 在表达式或方程中自由指标可以出现多次，但不得
在同项内出现两次，若在同项内出现两次则是哑指 标。例：
若i为自由指标
ji , j fi 0
ji , j fii 0
个独立的自由指标，其取值范围是1～n，则这个方
程代表了nk 个分量方程。在方程的某项中若同时出 现m对取值范围为1～n的哑指标，则此项含相互迭
加的nm个项。
27
Appendix A.1
张量分析初步
矢量和张量的记法，求和约定 符号ij与erst 坐标与坐标转换 张量的分量转换规律，张量方程 张量代数，商判则
3. 换标符号，具有换标作用。例如：
d s2 ij d xi d x j d xi d xi d x j d x j
即：如果符号的两个指标中，有一个和同项中其它 因子的指标相重，则可以把该因子的那个重指标换成 的另一个指标，而自动消失。
30
Appendix A.2
符号ij与erst
Appendix A.1
张量基本概念
★ 指标符号也适用于微分和导数表达式。例如，三维
空间中线元长度 ds 和其分量 dxi 之间的关系
d s d x1 d x2 d x3
2 2 2
2
2 可简写成： d s d xi d xi
场函数 f(x1, x2, x3) 的全微分：
21n1 22n2 23n3 T2
31n1 32n2 33n3 T3
18

第2章 张量分析(清华大学张量分析,你值得拥有)

第2章 张量分析(清华大学张量分析,你值得拥有)

( Nij ij )a j 0 det( Nij ij ) 0
利用指标升降关系 a为非0矢量 利用主不变量
N ( ) 3 J1N 2 J 2 J3N 0
二阶张量的标准形: 张量最简单的形式

非对称二阶张量
•
请研究以下领域的同学关注。 1、应变梯度理论，偶应力理论 2、电流场，电磁流变（有旋场）

x
x
椭圆曲线的坐标变换
正交变换可使椭圆曲线的方程由以下一般形式
ax bxy cy d 0
任意二阶张量将一线性相关的矢量集映射为线性相 关的矢量集：
(i)u(i) 0
i 1
l
l l 0 T (i)u(i) (i)(T u(i)) i 1 i 1
正则与退化的二阶张量
•
3D空间中任意二阶张量T将任意矢量组u，v，w映射 为另一矢量组，满足：
N S
1 p
S S1e1e1 S2e2e2 S3e3e3
Si N i
1 p
几种特殊的二阶张量

正张量的对数
N N1e1e1 N2e2e2 N3e3e3
ln N ln N1 e1e1 ln N2 e2e2 ln N3 e3e3
Nij N ji Ni j Nij Nij N ji N ij N ji

N 1 NT 1
( ) , ( ) , ( ) ,
N T 1 N 2 N T 3 N 3 N T 2 N 4
NT 4
N T ( 4 )

反对称张量与其转置张量分量及二者所对应的矩阵

二阶张量的行列式

张量分析课件

张量分析课件

P = ∑αij Ej （i=1,2,3） i
j =1
3
Pi′ = ∑ α i′j′ E j′ （i'=1,2,3）
j ′ =1
3
代 入
将一阶张量Ej和Pi的变换规律
Pi′ = ∑ Ai′i Pi
3
代 入
E j′ = ∑ Aj ′j E j
j =1
i =1 3
∑A
i =1
3
i ′i i
P = ∑∑ α i′j′ Aj′j E j
证： 刚体定轴转动:
ω
(Z轴)转轴
刚 体
(
)
v τi A ni O′ ri
v
刚体定轴转动
r2 r r I 质点：ij = m(rij δ ij − ( r )i ( r ) j ) O
v Ri
= m(δ ij xk xk − xi x j ) (i, j, k=1, 2, 3)
例3. 设质量为m的质点位于点（x1, x2, x3）, 证明在 正交变换下，由九个分量构成的一个物理量Iij是一个 二阶张量, 其中： I ij = m(δ ij xk xk − xi x j ) (i, j=1, 2, 3) —称Iij为质点的惯性积，有Iij定义的物理量叫惯性矩. 证： 质点：I ij = m(δ ij xk xk − xi x j ) (i, j, k=1, 2, 3) 九个分量:
δij在坐标变换后，其各个分量的值不变. 即在任意坐 标系中按上式定义的二价对称δ符号是一个二阶张量.
例3. 设质量为m的质点位于点（x1, x2, x3）, 证明在 正交变换下，由九个分量构成的一个物理量Iij是一个 二阶张量, 其中： I ij = m(δ ij xk xk − xi x j ) (i, j=1, 2, 3) —称Iij为质点的惯性积，有Iij定义的物理量叫惯性矩.

第2章 张量分析(6.8)

第2章 张量分析(6.8)

第2章 张量分析§2.1矢量空间、基、基矢1．线性矢量空间设有n 个矢量,1,2,,i i n =a ，它们构成一个集合R ，其中每个矢量i a 称为R 的一个元素。

如()i j i j +≠a a 唯一地确定R 的另一个元素，及i k a （k 为标量）也给定R 内唯一确定的元素，则称R 为线性（矢量）空间。

R 中的零元素记为O ，且具有i ⋅=O a O .2．空间的维数设i α为m 个标量，若能选取i α，使得10mi ii =α=∑a且i α不合为零，则称此m 个矢量线性相关，否则，称为线性无关。

例1 位于同一平面内的两个矢量1a 和2a （如图）是线性无关的，即11220α+α≠a a 若1α和2α为任意值，且不全为零。

例2 位于同一平面内的三个矢量1a ，2a ，3a 是线性相关的，则恒可找到1α,2α,3α（不全为零）使1122330α+α+α=a a a 如图： 21133''=α+αa a a集合R 内线性无关元素的最大个数称为集合或空间的维数。

设R 的维数为n ，则记为n R ，欧氏空间为3R 。

3．空间的基和基元素n R 中任意n 个线性无关元素的全体称为n R 的一个基。

基的每个元素称为基元素，由于n R 的n 确良基元素是线性无关的。

于是n R 内任一个元素r 可表示成基元素的线性组合。

设(1,2,,)i i n =a 为n R 的任选的基，则有：10ni ii ='α≠∑a，i α'为任意的不全为零的标量但总可选取00≠α及i α不全等于零，使得010ni i i =α=α=∑r a或者2a1a21x2x3xi i x =r e110()nnii i i i i ==α=-=ξα∑∑r a a①i αα,00≠ 不全等于零，所以i ξ不全等于零，且为有限值。

② n R 内有无限个基，但只有一个基是独立的，因为n R 内至少只有n 个元素是线性无关的。

第二章 张量分析

第二章 张量分析

a y x a y y a y z
az z az x az y
右梯度
grada a
a i e i e j

j

ai ei e j xj
ai , j ei e j
a ij e i e j
其中：
a ij
柱面坐标系 设直角坐标系为
曲线坐标系为
则式
i i
x x x
1 1
的具体形式取为：
i'
'
'
x
x
i'
i
: x1 , x 2 , x 3
1'

, x
3'
: x r, x
2'
z

x i' x x x 2 x 2 xi
x
3
x x z
3 i'
r cos r sin
x z C3 (常数)为垂直于z轴的平面；
3'
(iii)
和坐标曲线： (i) (ii) (iii)
x r C1和 x C2 的交线(z线)是直线；
dS1
dS3
d S1 d r2 d r3 d S2 d r3 d r1 d S3 d r1 d r2
a (P、Q、R)
根据Gauss定理有： 左边
(a1n1 a2 n2 a3n3 )dS
除
r 0
外，
J 0 ，故有逆变换的具体形式如下：
x
1'
r
'

2第02章张量分析(第01讲)

2第02章张量分析(第01讲)
一阶张量的记法：
①实体记法： U 3
∑ ②分解式记法：U = u1e1 + u2e2 + u3e3 = uiei
③分量记法 ui
i =1
二阶张量的记法：
2.2 矢量
2.2.1 2.2.2 2.2.3 2.2.4 2.2.5
矢量代数 标量积 矢量积 三重积 标量场和矢量场
2.2.1 矢量代数
矢量既有大小又有方向，在坐标系中通 常用箭头表示。
哈密顿算子
式中
∇=(∂ , ∂ , ∂ )
∂x ∂y ∂z
拉普拉斯算子
Δ = ∇⋅∇ = ∂2 + ∂2 + ∂2
∂x2 ∂y2 ∂z2
• 矢量的散度：
∇ ⋅V = ∂v1 + ∂v2 + ∂v3 ∂x ∂y ∂z
• 矢量的旋度：
e1
e2
∇ ×V = curlV = ∂ / ∂x ∂ / ∂y
v1
U ×V = −(V ×U ) U × (V ×W) ≠ (U ×V) ×W • 一个矢量与其自身的矢量积为零矢量。
• 应用：力F作用于位置矢量为r的点A，则力 F绕原点的力矩为：
M =r×F
2.2.4 三重积
• 三重标量积：
u1 u2 u3 U ⋅ (V ×W) = v1 v2 v3 = (U ×V) ⋅W
∂f ∂l
= lim
ρ →0
f ( x + Δx, y + Δy, z + Δz) − ρ
f ( x, y, z) ,
（ 其中 ρ = (Δx)2 + (Δy)2 + (Δz)2 ）
设方向 L 的方向角为α , β , γ .
当函数在此点可微时，那么函数在该点沿任意方

张量分析02

张量分析02

I.2 符号ij δ与rst e符号ij δ称为“Kronecker delta ”，它的定义是：⎩⎨⎧=01ij δ时当时当j i j i ≠= ()n ,,2,1j ,i = (I.14)定义表明它对指标i 和j 是对称的，即ji ij δδ= (I.15)ij δ的分量集合对应于单位矩阵。

例如，在三维空间中：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡10010001333231232221131211δδδδδδδδδ (I.16) 利用ij δ可以把线元长度平方的公式(I.6)改写成j i ij dx dx dsδ=2(I.17)这里ij δ起了换标的作用，即：如果ij δ符号的两个指标中，有一个和同项中其他因子的指标相重，则可以把该因子的那个重指标替换成ij δ的另一个指标，而ij δ自动消失。

这样：i i jj ji ij dx dx dxdx dxdx ds===δ2类似地有ik jk ij a a =δ；jk ik ij a a =δki kj ij a a =δ；kj ki ij a a =δ (I.18)以及ik jkij δδδ=；il kl jk ij δδδδ= (I.19)所以，ij δ也称为换标符号。

符号rst e 的定义是：⎪⎩⎪⎨⎧-=011rste 个以上指标值相同时中有当为逆序排列时当为正序排列时当2t ,s ,r t ,s ,r t ,s ,r (I.20a) 或)r t )(t s )(s r (21e rst ---=()3,2,1t ,s ,r = (I.20b)其中，正序排列是指（l , 2 . 3 ）及其轮流换位得到的（2 . 3 , l ）和（3 , 1 , 2 ），逆序排列是指（3 , 2 ,l ）及其轮流换位得到的（2 , l , 3 ）和（l , 3 , 2 ）。

rst e 称为排列符号或置换符号。

它共有27 个元素，其中只有3个元素为1，3个元素为－1 ，其余的元素都是0。

第2章-张量分析(清华大学张量分析-你值得拥有)PPT课件

第2章-张量分析(清华大学张量分析-你值得拥有)PPT课件

• 负整数次幂
G T 0 T 1(1) T 1 T 1 T T 1
T 2 T 1 T 1
T m T 1 T 1 T 1 T 1
几种特殊的二阶张量
➢ 正张量：N>0的对称二阶张量
uN u 0
➢ 非负张量：N≥0的对称二阶张量 u N u 0
对称二阶张量总可以化为：
N N1e1e1 N2e2e2 N3e3e3
能量密度。而大变形情况会出现高度非线性，则不能 用加法分解，而要用乘法分解。
• 最简单的坐标变换
y y
x cos sin x
y
sin
cos
y
x
• 椭圆曲线的坐标变换
x
正交变换可使椭圆曲线的方程由以下一般形式
ax2 bxy cy2 d 0
变换为最简形式，即两主轴坐标系下形式。
x a
2
y b
2
1
几种特殊的二阶张量
➢ 正交张量Q
• 正交张量的定义和性质
可证： Q e3 e3
Q e1 cos e1 sin e2 Q e2 cos e2 sin e1
e1, e2 整体绕轴向旋转一个角度
几种特殊的二阶张量
• 正交张量对应的正交变换的特性
① 保内积性质 ② 保长度性质 ③ 保角度性质
(Q u) (Q v) u v
(Q u) (Q u) u u
l i
Tii
J2
1 2!
T T ij l
lm i
m j
1 2
(TiiTll
TliTil )
J3
1 3!
T T ijk l
lmn i
Tm n
j k
det(T )

张量分析(全)

张量分析(全)

补充知识：张量分析1. 指标符号
2.矢量的基本运算
3.坐标变换与张量定义
4.张量的代数运算(1).加减法
(2).矢量与张量的点积（点乘）
(3).矢量与张量的叉积
(4).两个张量的点积
(5).张量的双点积
(6).张量的双叉乘
(7).张量的缩并
(8).指标置换
和（9）.对称化和反对称化
5.二阶张量（仿射量）概述
（1）.张量的转置B T
（2）.张量的逆B-1
（3）.对称仿射量的主向和主值
（4）.各向同性张量
6.张量分析
概述
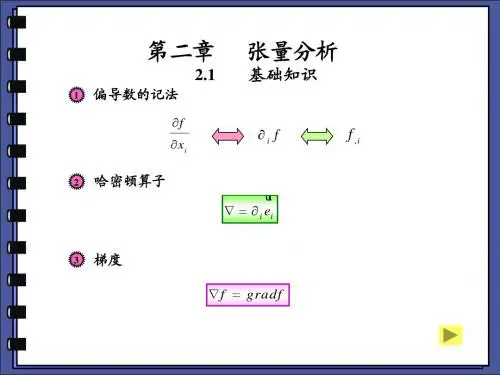
（1）.哈密尔顿算子（梯度算子）
（2）.张量场的微分
（3）.散度定理
7.曲线坐标系下的张量分析（1）.曲线坐标
（2）.局部基矢量
（3）.张量对曲线坐标的导数
END。

【张量分析ppt课件】张量分析课件第二章2 矢量函数共46页PPT资料

【张量分析ppt课件】张量分析课件第二章2 矢量函数共46页PPT资料

o
解：v ()vc o si1 vs ini2 (0 .5 c o s 0 .2 5 c o s 2)i1
(0 .5 s in 0 .2 5 s inc o s)i2 ; 0 /2 0 :v 0 .2 5 m / s ; 1 5 :v 0 .2 5 9 m / s
3 0 :v 0 .2 8 3 m / s ; 4 5 :v 0 .3 2 3 m / s
，b]区间的不同取值x (t)位置矢量平面描绘一条曲线。
对矢量函数： x x (t1 ,t2 ) x 1 (t1 ,t2 )i1 x 2 (t1 ,t2 )i2
t2
x2
当t = b 时： 2 2
x x (t1 ,b 2 ) x 1 (t1 ,b 2 )i1 x 2 (t1 ,b 2 )i2
a2
更一般地有：对矢量函数 x(t)的终点所描绘的曲线称为矢
端曲线或称为 x(t)的图形。而（2.3-1）式称为矢量方程。
ቤተ መጻሕፍቲ ባይዱ例12：
x2
已知小球在四分之一圆弧轨道中运动。圆弧
轨道半径R=50cm，小球运动速度的大小 v φ
0.51cos(m。/s)试求小球速度矢量方程；并在图
4
中画出小球速度的矢端曲线。
程。参数方程在 {o；i1，i2，i3} 中描绘的曲线称为矢端曲 线（面）。
具有一个参数的矢量函数矢端曲线（二维映射分析）：
设x = x (t) , b≤t≤a。在平面坐标系{o；i1，i2}中，矢量x
随t的变化，且： xx1(t)i1x2(t)i2
x2
x完全由x1(t), x2(t)的变化确定。
t*
xx(t1, ,tn)
（2.3-3）
x x 1 ( t 1 ,, t n ) i 1 x 2 ( t 1 ,, t n ) i 2 x 3 ( t 1 ,, t n ) i 3 x i ( t 1 ,, t n ) i i

张量分析第二讲精品PPT课件

张量分析第二讲精品PPT课件
i1,2,3
爱因斯坦求和约定
Sa 1x1a2x2anxn
n
n
S aixi ajxj
i1
j1
约定 Saixi ajxj
用拉丁字母表示3维，希腊字母表2
维
求和指
标与所用 的字母无
关
指标重
复只能一 次
指标范
围
33
Aij xi y j
i1 j1
双重求和
Aij xi yj A11x1y1A12x1y2 A13x1y3
i——自由指标，在每一项中只出现一次，一个公式 中必须相同
置换符号与克罗尼克尔记号
1 若i, j,k1,2,3,2,3,1,3,1,2 eijkeijk1 若i, j,k3,2,1,2,1,3,1,3,2
0 若有两个或三个等指
j i
1 0
当i j 当i j
ijaj i1a1i2a2i3a3ai imAmj i1A1j i2A2j i3A3j Aij
i
i
1 1
2 2
3 3
3
k
i
j
k
j i
j
i
i
j
i i
j j
3
j
i
k j
l k
l i
• 2. 张量相关的概念
P•g1(P1g1P2g2)•g1P1 P•g2(P1g1P2g2)•g2P2 P•g1(P1g1P2g2)•g1P1 P•g2(P1g1P2g2)•g2P2
gi gijgj
g i
gijg j
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
张量的加法和乘法运算与矩阵运算一一对应。
求迹运算，即缩并，对应于求3 矩阵的对角线元
素之和。 二阶张量与矢量的点积，即线性变换。例如：
w T u
该运算具有线性性质：
T (u v) T u T v
两个二阶张量的点积
只有取 2 ，3 矩阵时，才与矩阵乘法相对应。
二阶张量的某些运算没有对应的矩阵运算 6 例如，并乘运算。
(J1 )3
1 2
J1
J
2
1 3
J
3
以及
J1 J1
J
2
( J1 )2
2J2
J
3
( J1 )3
3J1J2
3J3
12
二阶张量的不变量（代数）
➢ 二阶张量T与三个线性无关矢量间的线性变换
T u v w u T v w u v T w J1T u v w
T u
T v
wu
T v
T w T u
v
T
w
J
T 2
u
v
w
T u
T v
T
w
J
T 3
u
v
w
.
正则二阶张量，有Nanson公式
T
u
T
v
J
T 3
TT
1 u v
13
二阶张量的标准形: 张量最简单的形式
.
➢ 实对称二阶张量的标准形
• 简单的例子
复杂应力状态分析中的主应力
σ ijeie j
σ 1e1e1 2e2e2 3e3e3
正则与退化的二阶张量
➢ 行列式值不为零的二阶张量T称为正则的，否则称 为退化的。
.
➢ 二阶张量将整个矢量空间中的任意矢量映射为矢量。 • 任意二阶张量将零矢量映射为零矢量：T 0 0
• 任意二阶张量将一线性相关的矢量集映射为线性相 关的矢量集：
l
(i)u(i) 0
i 1
0
T
l i 1
.
➢ 实对称二阶张量的标准形
存在以下等式：
N
g1
N 1 1
g1
N a a
N
g2
N 2 2
g2
特征方程，λ即N的特征
N g3 N特33 g征3 值为什么值是，三a即个N？的特征向量。
Nija j ai
分量形式
(Nij ij )a j 0
利用指标升降关系
det( Nij
i j
)
0
a为非0矢量
.
第2章 二阶张量
2021年3月16日
1
主要内容
.
二阶张量的矩阵
正则与退化的二阶张量
二阶张量的不变量
二阶张量的标准型
几种特殊的二阶张量
二阶张量的分解
正交相似二阶张量
2
二阶张量的矩阵
.
➢ 二阶张量的分量包含协变、逆变和两种混变形式
T
Tij gi g j
Ti j gi g j
T
i j
(i)u(i)
l
(i)(T
i 1
u(i))
7
正则与退化的二阶张量
.
• 3D空间中任意二阶张量T将任意矢量组u，v，w映射 为另一矢量组，满足：
T u T v T w detT u v w
➢ 正则二阶张量的特性：
• 正则的二阶张量T的转置张量TT也是正则的，正则的 二阶张量T存在唯一的逆T-1。
• 二阶张量T是正则的充要条件是 T u 0，当且仅当
u 0。
• 单射性。若 T u T v ， 则 u v
8
• 满射性。若 T u w，则存在唯一的逆变换 T 1 w u
.
二阶张量的不变量（代数）
➢ 力学是用张量的不变量写成的！
➢ Gorldan猜想：代数结构中有无穷多不变量，但基 本不变量只有有限个。
通常定义
T 3
的行列式为张量T的行列式
det T
det(
T 3
)
T
i j
det T T
由于两个互为转置的矩阵的行列式相等，所以
det(1T
T
)
det(
T 1
),
det(
T 4
T
)
det(
T 4
)
det(
T 2
T
)
det(
T 3
),
det(
T 3
T
)
det(
T 2
)
5
.
二阶张量的矩阵
➢ 二阶张量的代数运算与矩阵的代数运算
(
N 2
)T
,
N 4
N 4
T
(
N 4
)T
➢ 反对称张量与其转置张量分量及二者所对应的矩阵
ij ji
j i
i j
i j
ji
ij ji
1
1
T
(1
)T
,
2
(
3
)T
,
3
(
2
)T
,
4
4
T
(
4
)T
4
二阶张量的矩阵
➢ 二阶张量的行列式
.
det(1) g det( 2 ) g det(3) g 2 det( 4 )
15
()
3
J1N 2
伟大的抽象代数之母诺特，石 破天惊的思想： 任何对称性，都对应某种形式 的守恒律！！
9
埃米·诺特 Emmy Noether （1882-1935）
.
二阶张量的不变量（代数）
➢ 二阶张量T的标量不变量：
G
:T
G
T
Tii
tr(T )
C1
T i i
（力学中，11 22 33 对应静水应力）
T
:T
gi
g
j
T ij gi g j
➢ 以上四种分量形式对应着张量的四种矩阵形式
1 Tij
2 Ti j
3
T
i j
4 T ij
其中， 3矩阵是最重要的张量矩阵。
➢ 二阶张量的转置张量
WHY?
T T Tji gi g j Tij gi g j Tji gi g j T ji gi g j
3
二阶张量的矩阵
➢ 二阶张量的转置张量所对应的矩阵
TT 1
(
T 1
)T
TT 2
(
T 3
)T
TT 3
(
T 2
)T
TT 4
(
T 4
)T
.
➢ 对称张量与其转置张量分量及二者所对应的矩阵
Nij N ji
N
i
j
Nij
Nij
N
i j
N ij N ji
1N
N 1
T
(1N
)T
,
N 2
(
N 3
)T
,
N 3
应力张量的三个主方向是正交的。
• 对称二阶张量 N Nij gi g j 必定存在一组正交基矢量 g1 ，g2 ，g3 ，使得
N
N 1 1
g1
g1
N 2 2
g2
g
2
N 3 3
g3
g
3
则 N11，N22，N33 为N的主分量，g1 ，g2 ，g3为N的主方向14 。
二阶张量的标准形: 张量最简单的形式
T
Ti j
j i
tr(T
T)
C2
T
Ti j
j i
ijk
T T T lmn i j k l m n
C3
10
二阶张量的不变量（代数）
.
➢ 二阶张量T的三个主不变量：
J1
G :T
Ti l
l i
Tii
J2
1 2!
T T ij l
lm i
m j
1 2
(TiiTll
TliTil )
J3
1 3!
T T ijk l
lmn i
Tm n
j k
det(T )
➢ 二阶张量T的矩：
J1 tr(T ) Tii

2
tr(T
T)
T
Ti j
j i
J
3
tr(T
T
T)
T
T T i j k
j k i
11
二阶张量的不变量（代数）
.
➢ 二阶张量T的三个主不变量与各阶矩之间的关系
J1 J1
J2
1 2
(J1 )2
J
2
J3
1 6