张量分析习题

张量习题参考答案张量习题参考答案张量作为数学和物理学中的重要概念，经常出现在各种习题中。

在学习张量的过程中，我们常常会遇到一些难以理解或者复杂的习题。

本文将为大家提供一些张量习题的参考答案，帮助大家更好地理解和掌握这一概念。

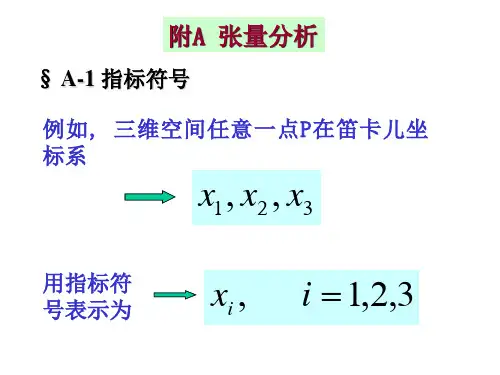
1. 张量的定义和性质习题：请定义张量，并列举一些张量的性质。

参考答案：张量是向量和矩阵的推广，是具有多个分量的多维数组。

它在数学和物理学中有着广泛的应用。

张量的性质包括：线性性、分量的变换规律、坐标系无关性、张量的积、张量的收缩等。

2. 张量的坐标变换习题：已知张量T在坐标系A下的分量为T^i_j，在坐标系B下的分量为T^k_l，求坐标变换关系。

参考答案：根据张量的变换规律，我们有T^k_l = ∂x^k/∂x^i * ∂x^j/∂x^l *T^i_j，其中∂x^k/∂x^i和∂x^j/∂x^l分别为坐标系A和坐标系B之间的转换矩阵。

通过求解这个方程组，我们可以得到坐标变换关系。

3. 张量的积习题：已知两个张量A和B，分别为A^i_j和B^k_l，请计算张量的积C=A*B。

参考答案：张量的积是通过分量的乘法和求和得到的。

对于C^i_l = A^i_j *B^j_l，我们可以通过对A和B的分量进行乘法运算，并对j进行求和，得到C的分量。

4. 张量的收缩习题：已知一个二阶张量T的分量为T^i_j，请计算张量的收缩。

参考答案：张量的收缩是通过对张量的分量进行乘法和求和得到的。

对于T^i_i，我们可以对i进行求和，得到收缩的结果。

5. 张量的应用习题：请列举一些张量在物理学中的应用。

参考答案：张量在物理学中有着广泛的应用。

例如，在相对论中，能动张量描述了物质和能量的分布；在电磁学中，麦克斯韦张量描述了电磁场的性质；在流体力学中，应力张量描述了流体的运动和变形等。

总结：本文提供了一些张量习题的参考答案，希望能够帮助大家更好地理解和掌握张量的概念和性质。

通过解答这些习题，我们可以加深对张量的理解，并将其应用于实际问题中。

2 二阶张量及其若干运算法则(一) 概念、理论和公式提要2-1 张量的乘法① 张量的外乘(并乘) 张量的外乘用⊗表示，其外积为张量，其阶数等于外乘诸张量阶数之和。

② 张量的内乘(点乘) 张量的点乘用“·”表示(有时也可省去“·”)，其内积为张量，其阶数为内乘诸张量阶数之和减去2倍内乘的次数。

③ 张量的双点乘记作“∶”(两次点乘)，例如B A∶；其积为张量，其阶数为诸张量阶数之和减2倍点乘次数。

设)(CT )(CT )(CT p n m 为，为，为C B A ，则)42(CT ⨯-++=p n m 为，∶∶D D C B A (2-1-1) 取)2(CT 244为，则，，D ===p n m ，其分量为rp mnrp ijmn ij C B A D = (2-1-2)其中A 分量的后两个指标与B 分量的前两个指标，B 分量的后两个指标与C 分量的前两个指标依次相同。

④ 二阶张量ij ij T T =T T T T ∶，定义为的范数记为为正方根，且有时才取等号只当，o T T =≥0 (2-1-3) 的绝对值为标量，ααααT T = (2-1-4) R T R T +≤+ (2-1-5) R T R T ⋅≤∶ (2-1-6) a T a T ≤⋅ (2-1-7)R a a 的模，为矢量亦为二阶张量。

⑤ 设C B A B A 次缩拼为张量外积的和，则和分是是和s t r )(CT )(CT ，记为C B A =⊗s C)2(s t r -+为C 阶张量，其分量关系为mn k k k k k k ij mn ij s s B A C 2121= (2-1-8)反之，如果已知C B 和为张量，其分量与带指标的量 ij A 满足上式，则 ij A 为张量A 的分量，称为商法则或张量识别定理。

A 的阶数等于s 2的阶数加C ，减去B 的阶数。

特别地当B ，t s =的分量的全部指标都是哑标时，则A 的阶数等于B 和C 的阶数之和。

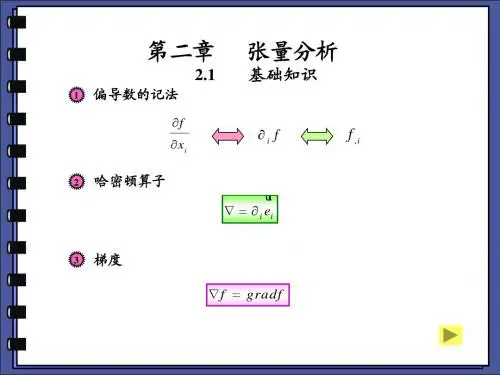
第二章 正交曲线坐标系下的张量分析与场论1、用不同于书上的方法求柱坐标系和球坐标系的拉梅系数及两坐标间的转换关系ij β。

解：①柱坐标系k z j i r++=ϕρϕρs i n c o s ，2222222dz H d H d H ds z ++=ϕρϕρ ()()k dz j d d i d d r d+++-=ϕϕρρϕϕϕρρϕcos sin sin cos()()222222222222222222222222222222c o s s i n s i n c o s c o s s i n 2c o s s i n s i n c o s s i n 2c o s c o s s i n s i n c o s dz d d dz d d d d dz d d d d d d d d dz d d d d r d r d ds ++=++++=+++++-=+++-=⋅=ϕρρϕϕρϕϕρρϕρϕϕρϕϕρϕϕρρϕϕϕρϕρϕϕρρϕϕϕρρϕϕϕρρϕ故：1=ρH ，ρϕ=H ，1=z H ②球坐标系k R j R i R r θφθφθc o s s i n s i n c o s s i n ++=，2222222φθφθd H d H dR H ds R ++=()()()kd R dR j d R d R dR id R d R dR r dθθθφφθθφθφθφφθθφθφθsin cos cos sin sin cos sin sin sin sin cos cos cos sin -++++-+= ()()()2222222222s i n s i n c o s c o s s i n s i n c o s s i n s i ns i n s i n c o s c o s c o s s i n φθθθθθφφθθφθφθφφθθφθφθd R d R dR d R dR d R d R dR d R d R dR r d r d ds ++=-++++-+=⋅=故：1=R H ，R H =θ，θφsin R H = ③两坐标间的转换关系ij βφr re e θe φPθru re e zu ze r(1)圆柱坐标系 （2）球坐标系由球坐标系与直角坐标系的坐标变换矩阵为：sin cos sin sin cos cos cos cos sin sin sin cos 0r e i e j e k θφθφθφθθφθφθφφ⎧⎫⎧⎫⎡⎤⎪⎪⎪⎪⎢⎥=-⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥-⎣⎦⎩⎭⎩⎭注意，圆柱坐标系中的θ和球坐标系的φ相等。

张量习题答案张量习题答案张量是数学中一个重要的概念，广泛应用于物理学、工程学等领域。

它是一个多维数组，可以用来表示向量、矩阵和更高维的数据结构。

张量的运算和性质十分复杂，因此在学习张量的过程中，习题是不可或缺的一部分。

下面我将为大家提供一些张量习题的答案，希望能对大家的学习有所帮助。

1. 习题：给定两个向量a = (1, 2, 3)和b = (4, 5, 6)，求a和b的内积。

答案：内积是两个向量对应分量的乘积之和。

所以，a和b的内积可以表示为：a·b = 1×4 + 2×5 + 3×6 = 4 + 10 + 18 = 32。

2. 习题：已知一个3×3的矩阵A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]，求矩阵A的转置。

答案：矩阵的转置是将矩阵的行和列互换得到的新矩阵。

对于矩阵A来说，它的转置可以表示为：A^T = [[1, 4, 7], [2, 5, 8], [3, 6, 9]]。

3. 习题：已知一个2×2的矩阵B = [[2, 3], [4, 5]]，求矩阵B的特征值和特征向量。

答案：特征值和特征向量是矩阵在线性代数中的重要概念。

对于矩阵B来说，我们可以通过求解特征方程来求得其特征值和特征向量。

特征方程可以表示为：det(B - λI) = 0，其中I是单位矩阵，det表示行列式。

解特征方程可以得到矩阵B的特征值。

然后，将每个特征值代入(B - λI)x = 0，求解得到特征向量。

具体计算过程略。

4. 习题：已知一个3维张量C，其形状为(2, 3, 4)，求张量C的元素个数。

答案：张量的元素个数等于各个维度的乘积。

对于张量C来说，其元素个数可以计算为：2 × 3 × 4 = 24。

5. 习题：已知一个2维张量D，其形状为(3, 3)，求张量D的逆矩阵。

答案：逆矩阵是在线性代数中常用的概念，对于方阵来说，如果存在逆矩阵，那么该矩阵是可逆的。