运筹学应用实例分析

简单的运筹学实际应用案例运筹学（Operations Research）是一门研究如何有效利用有限资源进行决策的学科，它通过数学、统计学和经济学等方法，帮助管理者做出最佳决策。

下面将介绍几个简单的运筹学实际应用案例。

1.生产线优化假设一公司拥有多条生产线，每条生产线对应不同的产品。

公司希望通过优化生产线的调度，以达到最大的产出和利润。

运筹学可以通过数学模型和算法，对生产线进行优化调度。

例如，可以使用线性规划模型来确定每条生产线的产量和调度，以最大化总利润；也可以使用整数规划模型来考虑生产线的限制和约束条件。

2.物流网络设计一家物流公司需要设计其物流网络，以最小化成本并满足客户对快速物流的需求。

运筹学可以通过数学模型和算法，帮助物流公司优化物流网络的设计。

例如，可以使用网络流模型来确定货物在物流网络中的最佳路线和节点，以最小化总运输成本；也可以使用线性规划模型来决定在不同节点上的仓库和货物库存量，以满足客户的需求。

3.航班调度问题一家航空公司需要制定最佳航班调度计划，以最大化航班利润并排除延误风险。

运筹学可以通过数学模型和算法，帮助航空公司优化航班调度。

例如，可以使用线性规划模型来决定不同航班的起降时间和机型，以最大化航班利润；也可以使用排队论模型来评估航班的延误风险，并制定相应的调度策略。

4.人员调度问题一家超市需要制定最佳的员工调度计划，以最大化服务质量和节约人力成本。

运筹学可以通过数学模型和算法，帮助超市优化员工调度。

例如，可以使用整数规划模型来决定不同时间段需要多少员工，并考虑员工的技能匹配和工作时间的合理安排；也可以使用模拟仿真方法来评估不同调度策略的效果，并做出相应的决策。

以上是几个简单的运筹学实际应用案例，运筹学在实际生产和管理中有着广泛的应用。

通过数学模型和算法的应用，可以帮助企业优化资源配置、提高效率和决策质量，从而实现最佳的经济效益。

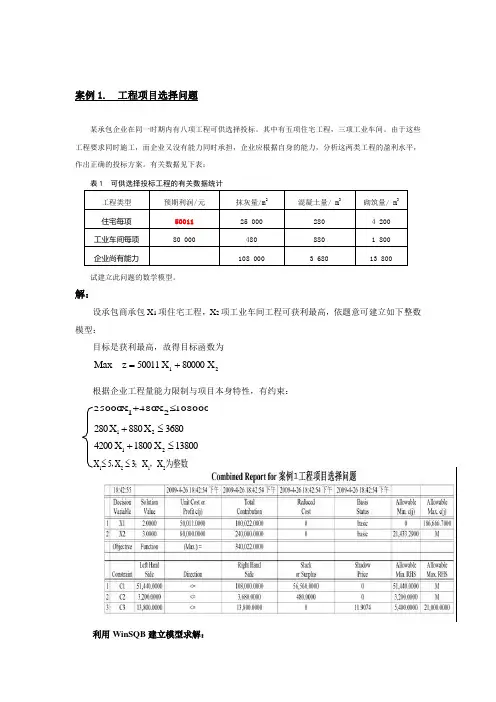
案例1. 工程项目选择问题某承包企业在同一时期内有八项工程可供选择投标。

其中有五项住宅工程，三项工业车间。

由于这些工程要求同时施工，而企业又没有能力同时承担，企业应根据自身的能力，分析这两类工程的盈利水平，作出正确的投标方案。

有关数据见下表：表1 可供选择投标工程的有关数据统计工程类型 预期利润/元 抹灰量/m 2混凝土量/ m 3砌筑量/ m 3住宅每项 50011 25 000 280 4 200 工业车间每项 80 000480 880 1 800 企业尚有能力108 0003 68013 800试建立此问题的数学模型。

解：设承包商承包X 1项住宅工程，X 2项工业车间工程可获利最高，依题意可建立如下整数模型：目标是获利最高，故得目标函数为21X 80000X 50011z Max +=根据企业工程量能力限制与项目本身特性，有约束：利用WinSQB 建立模型求解：1080002X 4801X 25000≤+3680X 880X 28021≤+13800X 1800X 420021≤+为整数，；，2121X X 3X 5X ≤≤综上，承包商对2项住宅工程，3项车间工程进行投标，可获利最大，目标函数Max z=340022 元。

案例2. 生产计划问题某厂生产四种产品。

每种产品要经过A，B两道工序加工。

设该厂有两种规格的设备能完成A工序，以A1 ，A2表示；有三种规格的设备能完成B工序，以B1 ，B2，B3 表示。

产品D可在A，B任何一种规格的设备上加工。

产品E可在任何规格的A设备上加工，但完成B工序时只能在B1设备上加工。

产品F可在A2及B2 ，B3上加工。

产品G可在任何一种规格的A设备上加工，但完成B工序时只能在B1 ，B2设备上加工。

已知生产单件产品的设备工时，原材料费，及产品单价，各种设备有效台时如下表，要求安排最优的生产计划，使该厂利润最大？设设产品设备有效台时1 2 3 4A1 A2 B1 B2 B357647109812111068108601110000400070004000原料费（元/件）单价（元/件）0.251.250.352.000.502.800.42.4解：设Xia(b)j为i产品在a(b)j设备上的加工数量,i=1,2,3,4;j=1,2,3，得变量列表设备产品设备有效台时Ta(b)j1 2 3 4A1 A2 B1 B2 B3X1a1X1a2X1b1X1b2X1b3X2a1X2a2X2b1X3b2X3b3X3a1X3a2X3b1X3b2X3b3X4a1X4a2X4b1X4b2X4b3601110000400070004000原料费Ci （元/件） 单价Pi （元/件） 0.25 1.25 0.352.00 0.50 2.80 0.4 2.4其中，令X 3a 1，X 3b 1，X 3b 2，X 3b 3，X 4b 3=0 可建立数学模型如下： 目标函数: ∑∑==-=4121)](*[Maxi j iaj Ci Pi X z=1.00*（X 1a 1+X 1a 2）+1.65*（X 2a 1+X 2a 2）+2.30* X 3a 2+2.00*（ X 4a 1+X 4a 2）约束条件：利用WinSQB 求解（X1~X4，X5~X8,X9~X12,X13~X17,X18~X20分别表示各行变量）：4,3,2,1X21j 31==∑∑==i X j ibjiaj2,1T X 41iaj=<=∑=j Taj i iaj 3,2,141=<=∑=j TbjT Xi ibj ibj2,1;4,3,2,10X iaj ==>=j i 且为整数32,1;4,3,2,10X ibj ，且为整数==>=j i 0X X X X X 4b33b33b23b13a1=====综上，最优生产计划如下：设备产品1 2 3 4A1 A2 B1 B2 B3774235004004008732875目标函数zMax=3495，即最大利润为3495案例3. 高校教职工聘任问题 （建摸）由校方确定的各级决策目标为：P 1 要求教师有一定的学术水平。

运筹学在实际问题中的应用案例分析运筹学作为一门研究如何最优化地解决决策问题的学科，在实际问题中得到了广泛的应用。

本文将通过分析两个实际案例来探讨运筹学在解决复杂问题和优化资源利用方面的应用。

案例一：物流配送优化物流配送是一个典型的运筹学应用领域。

在现代社会，物流配送环节对于企业的运营效率和成本控制至关重要。

如何合理安排车辆路线、调度和配送是一项复杂且具有挑战性的任务。

运筹学可以通过数学建模和优化算法来解决这个问题。

首先，我们可以将物流配送问题建模为一个旅行商问题（Traveling Salesman Problem，TSP）。

TSP是一个经典的组合优化问题，目标是寻找一条最短路径，使得从一个地点出发经过所有其他地点后回到起点，且路径的总长度最小。

通过运筹学方法，可以利用算法来求解最佳路径并优化物流配送效率。

其次，为了进一步优化物流配送的效率，我们可以引入车辆调度问题。

例如，考虑到不同城市的交通堵塞情况，我们可以使用调度算法将不同城市的订单分配给不同的车辆，以减少整体行程时间和成本。

通过运筹学的应用，一家物流公司可以最大限度地减少行程时间、减少燃料消耗，提高物流配送的效率。

因此，运筹学在物流配送问题中的应用具有重要的意义。

案例二：生产排产优化生产排产是制造业中的一个重要环节，它关系到企业的生产效率、生产能力和订单交付时间。

运筹学在生产排产中的应用可以帮助企业提高生产效率，降低成本并及时交付产品。

在生产排产中，我们通常需要考虑到多个因素，如机器的利用率、工人的工作时间和任务的优先级等。

通过运筹学的方法，可以构建一个数学模型，通过数学规划算法来优化生产排产方案。

例如，假设一个工厂有多个机器和多个订单需要排产，每个订单有不同的完成时间和优先级。

我们可以通过运筹学的方法，将这个问题建模为一个调度问题。

然后，利用调度算法来确定每个订单的完成时间和最优的生产顺序，从而实现生产排产的优化。

通过运筹学的应用，企业可以有效地优化生产排产计划，提高生产效率，减少资源浪费，并保证订单能够及时交付。

生活中运筹学案例分析
运筹学是一门研究如何做出最优决策的学科，它在生活中有着广泛的应用。

从
日常生活中的购物决策到企业的生产计划，都可以看到运筹学的影子。

在本文中，我们将通过一些生活中的案例来分析运筹学的应用。

首先，让我们来看一个购物决策的案例。

假设你需要购买一件衣服，而且你有
多个选择。

每件衣服的价格、品质、风格都不同，你需要在这些选择中做出最优的决策。

这时，你可以运用运筹学的方法，比如成本效益分析、决策树分析等，来帮助你做出最佳选择，从而在有限的预算内获得最大的满意度。

其次，让我们来看一个企业生产计划的案例。

假设一个工厂需要生产多种产品，并且有限的资源，比如人力、原材料、机器等。

在这种情况下，工厂需要合理安排生产计划，以最大化产出并降低成本。

这就需要运用运筹学的方法，比如线性规划、排程算法等，来优化生产计划，使得工厂能够以最有效的方式进行生产。

此外，运筹学还可以应用于交通运输、物流配送、金融投资等方面。

比如，在
交通运输中，如何合理安排车辆的路线，以最小化时间和成本；在物流配送中，如何优化仓储和配送流程，以提高效率和降低成本；在金融投资中，如何构建最佳的投资组合，以最大化收益和降低风险。

综上所述，运筹学在生活中有着广泛的应用，可以帮助我们在各种决策中做出
最优选择。

通过分析一些生活中的案例，我们可以更好地理解和应用运筹学的方法，从而提高我们的决策能力和生活质量。

希望本文能够对读者有所启发，让大家在生活中更加注重运筹学的应用。

运筹学在工业领域的应用案例运筹学是一门研究如何通过数学模型和优化方法来解决实际问题的学科。

它广泛应用于工业领域，帮助企业提高生产效率、优化资源利用以及优化决策。

本文将以一些实际案例来展示运筹学在工业领域的应用。

案例一：物流调度在现代物流中心，卡车调度是一个重要而复杂的问题。

一家物流企业面临着如何合理安排卡车的运输路线以及如何将货物分配给不同的卡车的问题。

运筹学通过建立数学模型和优化算法，可以帮助企业快速找到最佳的调度方案。

通过考虑货物的重量、体积、运输距离等因素，运筹学能够帮助企业节省时间和成本，提高物流效率。

案例二：生产计划在工业生产中，合理的生产计划对企业的运营至关重要。

运筹学可以通过建立生产计划的数学模型，考虑原材料、人力资源、设备利用率等因素，制定最优的生产计划。

这种方法可以帮助企业合理安排生产任务、减少生产成本，并确保产品按时交付。

案例三：库存管理有效的库存管理对于企业的正常运营非常重要。

过多的库存会增加企业的成本，而库存不足则会导致订单无法及时完成。

运筹学可以利用数学模型和优化算法，预测需求并制定合理的库存策略。

通过运筹学的方法，企业可以实时调整库存水平，减少库存成本，同时确保生产进度和客户需求之间的平衡。

案例四：供应链优化供应链优化是一个复杂的问题，涉及到多个环节和多个参与者之间的协调。

运筹学可以帮助企业建立供应链的数学模型，考虑供应商、生产商、分销商等各个环节的需求和约束，通过优化算法找到最佳的供应链配置方案。

通过运筹学的方法，企业可以提高供应链的响应速度和灵活性，降低整体成本，提供更好的服务。

案例五：设备维护与优化在工业领域，设备的维护和优化是保证生产连续性和降低成本的关键。

运筹学可以利用数据分析和模型建立，制定设备的维护计划和优化方案。

通过预测设备故障、制定维护策略和排班方案，运筹学可以帮助企业降低设备故障率，最大限度地提高设备利用率，进而提高生产效率和降低成本。

综上所述，运筹学在工业领域有着广泛的应用。

生活中运筹学案例分析生活中的许多情境都可以运用运筹学的理念和方法来进行分析和优化。

下面我将通过几个生活中的案例来说明运筹学在实际生活中的应用。

首先，我们来看一个日常生活中的例子，早晨出门上班。

在早晨高峰期，许多人都面临着上班迟到的问题。

这时候我们可以运用运筹学的方法来优化出行路线。

比如，我们可以提前规划好最佳的出行路线，避开交通拥堵的路段，选择合适的出行工具，比如地铁、公交等，以最快的速度到达目的地，从而减少出行时间，提高效率。

其次，我们来看一个生产管理中的案例，生产调度。

在工厂的生产中，如何合理安排生产任务和生产资源是一个重要的问题。

我们可以借助运筹学的方法，通过对生产任务的分析和排程，合理安排生产顺序和生产线的利用率，从而提高生产效率，降低生产成本。

再次，我们来看一个物流配送中的案例，快递配送。

在快递行业中，如何合理安排快递的配送路线和时间是一个关键问题。

我们可以利用运筹学的方法，通过对快递订单的分析和规划，合理安排配送路线和配送顺序，以最短的时间和最低的成本完成配送任务，提高配送效率，提升客户满意度。

最后，我们来看一个市场营销中的案例，促销活动。

在市场营销中，如何制定合适的促销策略是至关重要的。

我们可以运用运筹学的方法，通过对市场需求和产品销售情况的分析，制定合理的促销策略和销售计划，最大限度地提高销售额，实现市场目标。

通过以上几个案例的分析，我们可以看到运筹学在生活中的广泛应用。

无论是日常生活、生产管理、物流配送还是市场营销，都可以通过运筹学的方法来优化资源配置，提高效率，降低成本，实现最佳的决策和规划。

希望大家在生活和工作中能够更多地运用运筹学的理念和方法，从而取得更好的效果。

《运筹学》案例分析案例1：超级食品公司的广告混合问题超级食品公司的营销部副总裁克莱略·希文生正面临着一个棘手的挑战：如何才能大规模地进入已有许多供应商的早点谷类食品市场。

值得庆幸的时，该公司的早点谷类食品“脆始”（Crunchy Start）有许多受欢迎的优点：口味佳、营养、松脆。

克莱略·希文生对这一切都如数家珍，她知道这一食品是能够赢得这次促销活动的。

然而，克莱略清楚她必须避免上一次产品促销活动中所犯的错误。

那是她晋升以后第一项重大任务，结果简直是个悲剧！她本以为已经大功告成，却没想到那次活动并没有触及至关重要的目标市场——幼年儿童以及幼年儿童的父母。

同时，她还领悟到未将优惠卷包含在杂志与报纸的广告中是另一大失误。

哎，学习是永无止境的。

这一次，必须吸取上次的教训。

公司的总裁大卫·斯隆已经向她表示脆始这一产品成功与否对公司前途有着重要影响。

她清楚地记得大卫在结束与她的谈话时说：“公司的股东对公司的现状极为不满，我们必须再次纠正方向，增加公司收入。

”克莱略以前也曾听到过这样的语调，但这一次，她从大卫极为严肃的目光中意识到了问题的严重性。

克莱略在攻读MBA管理运筹学课程时，曾经学习过如何通过建立数学模型来解决管理决策问题。

现在是时候让她仔细考虑一下问题，并准备应用所学知识解决问题了。

问题克莱略已经雇佣了一家一流的广告公司G&J公司来帮助设计全国性的促销活动，以使脆始取得尽可能多的消费者的认可。

超级食品公司将根据该广告公司所提供的服务付给一定的酬金（不超过100万美元）并已经预留了另外的400万美元作为广告费用。

G&J公司已经确定了这一产品最有效的三种广告媒介：媒介1：星期六上午儿童节目的电视广告。

媒介2：食品与家庭导向的杂志上的广告。

媒介3：主要报纸星期天增刊上的广告。

现在，要解决的问题是如何确定各广告活动的使用水平（levels）以取得最有效的绩效。

为了确定这一广告投放问题的最佳活动水平组合，首先必须明确该问题的总绩效测度（overall measure of performance）以及每一活动对该测度的贡献。

运筹学经典案例运筹学是一门研究在有限资源下进行有效决策的学科，它涉及到数学、经济学、管理学等多个领域。

在现实生活中，我们经常会遇到需要做出决策的情况，而运筹学正是帮助我们在复杂的情况下做出最优决策的学科。

下面，我们将介绍一些运筹学的经典案例，希望能够帮助大家更好地理解运筹学的应用。

1. 供应链优化。

供应链优化是运筹学中非常重要的一个领域，它涉及到如何在有限的资源下，实现最佳的供应链效率。

一个经典的案例是，某公司需要将产品从生产地运送到各个销售点，而在运输过程中需要考虑到运输成本、时间、货物损耗等多个因素。

通过运筹学的方法，可以帮助公司找到最佳的运输方案，从而降低成本、提高效率。

2. 生产排程优化。

在工厂生产过程中，如何合理地安排生产顺序和时间，是一个典型的运筹学问题。

通过对生产设备的利用率、生产时间、生产成本等因素进行综合考虑，可以利用运筹学的方法找到最优的生产排程，从而提高生产效率，降低生产成本。

3. 库存管理。

对于零售商来说，如何合理地管理库存是一个关键问题。

库存过多会增加成本，而库存过少又会导致无法满足客户需求。

通过运筹学的方法，可以帮助零售商找到最佳的库存管理策略，使得库存成本和客户满意度达到最优平衡。

4. 交通规划。

在城市交通规划中，如何合理地安排交通流量、制定最佳的交通信号灯配时方案等，都是典型的运筹学问题。

通过对交通流量、道路容量、交通需求等因素进行分析和优化，可以帮助城市交通管理部门制定出更加合理的交通规划方案，提高交通效率，减少拥堵。

5. 项目管理。

在企业项目管理中，如何合理地安排资源、时间和任务分配，是一个重要的问题。

通过运筹学的方法，可以帮助项目经理制定出最佳的项目计划，提高项目执行效率，降低项目成本，确保项目顺利完成。

总结。

运筹学在现实生活中有着广泛的应用，它帮助我们在复杂的决策情况下找到最佳解决方案，提高效率，降低成本。

通过对供应链优化、生产排程、库存管理、交通规划、项目管理等经典案例的分析，我们可以更好地理解运筹学的应用，希望大家能够在实际工作中运用运筹学的方法，解决复杂的决策问题，取得更好的效果。

生活中运筹学案例分析运筹学是一门研究如何在有限资源下做出最佳决策的学科，它的应用范围非常广泛，涉及到生产、物流、交通、金融等各个领域。

在生活中，我们也可以运用运筹学的方法来解决一些实际问题。

下面，我们就来看一个生活中的运筹学案例。

某家电商公司在双十一期间需要安排快递员送货上门，为了提高效率和降低成本，他们需要合理安排快递员的路线。

假设有5个快递员，需要分别送货到10个地点，每个地点的货物数量不同，送货的时间也不同。

现在，他们需要运用运筹学的方法来确定每个快递员的最佳路线，以最大限度地提高送货效率。

首先，他们需要收集每个地点的货物数量和送货时间，然后使用运筹学中的最优路径算法来确定每个快递员的最佳路线。

最优路径算法可以帮助他们找到每个快递员的最短路径，从而在最短的时间内完成送货任务。

其次，他们还可以运用运筹学中的分配算法来平衡每个快递员的工作量，确保每个快递员都能够在相同的时间内完成送货任务。

这样不仅可以提高效率，还可以减少快递员之间的工作差距。

最后，他们还可以使用运筹学中的排程算法来确定每个快递员的出发时间，以最大限度地减少等待时间和空载时间，从而提高整个送货过程的效率。

通过运用运筹学的方法，这家电商公司成功地解决了快递员配送路线的问题，提高了送货效率，降低了成本，为双十一期间的顺利进行提供了有力支持。

生活中的运筹学案例告诉我们，运筹学不仅仅是一门理论学科，它在实际生活中也有着重要的应用价值。

通过合理运用运筹学的方法，我们可以更好地解决一些实际问题，提高效率，降低成本，为生活带来更多的便利和效益。

因此，我们应该更加重视运筹学的学习和应用，努力将其运用到实际生活中，为我们的生活带来更多的便利和效益。

运筹学在生活中的例子
运筹学是一门研究如何做出最佳决策的学科，它在各个领域都有着广泛的应用。

从日常生活中的时间管理到复杂的商业运营决策，都可以看到运筹学的身影。

下面我们就来看看运筹学在生活中的一些例子。

首先，让我们来看看日常生活中的时间管理。

每天我们都需要面对各种各样的
任务和活动，如工作、家务、社交等。

如何合理安排时间，让每一件事情都能得到充分的安排，就需要运用运筹学的方法。

比如，我们可以利用时间表来规划每天的活动，将重要的任务优先安排，避免时间的浪费和碎片化，从而提高工作效率。

另一个例子是在商业领域中的供应链管理。

在现代商业运营中，供应链管理是
非常重要的一环。

通过运筹学的方法，可以帮助企业优化供应链的运作，降低成本、提高效率。

比如，利用运筹学的方法可以帮助企业确定最佳的库存水平，避免过多或过少的库存，从而降低库存成本和避免缺货现象的发生。

此外，运筹学还可以应用在交通规划中。

比如，城市交通拥堵是一个普遍存在
的问题，如何合理规划交通路线，减少拥堵，提高交通效率，就需要运用运筹学的方法。

通过分析交通流量、优化信号灯控制、调整道路规划等方式，可以帮助城市降低交通拥堵，提高交通效率。

总的来说，运筹学在生活中有着广泛的应用，它可以帮助我们合理安排时间、
优化商业运营、改善交通状况等。

通过运用运筹学的方法，我们可以做出更加理性和科学的决策，从而提高效率，降低成本，改善生活质量。

因此，我们应该更加重视运筹学的学习和应用，让它成为我们生活中的得力助手。

运筹学应用实例分析[整理]
运筹学是研究有关决策问题的一门科学。

它可以帮助人们高效地解决复杂的决策问题，并发现比其他方法更有效的解决方案。

运筹学的主要应用实例包括产品设计和调度，材料
需求计划和财务管理，以及货运路径规划和路线优化等等。

总的来说，运筹学应用的成功
建立在以下四个应用实例上：
1、产品设计和调度: 运筹学用于建立最佳产品设计和有效分配活动资源。

它可以帮
助企业最大化他们的产出和最小化生产成本。

它还可以降低企业的周期时间，降低能源消耗，提高生产灵活性，以便提高效率。

2、材料需求计划和财务管理: 运筹学也用于材料需求计划和财务管理，是创建可衡
量的决策系统的基础。

材料调度可以用来计算最佳采购量，用于预测需求，控制存货，改
善公司的投资组合和业务流程等。

3、货运路径规划和路线优化: 运筹学也可以用于路径规划和路线优化，以实现交通
路线最优化结果。

4、排序和调度问题: 最后，运筹学用于排序和调度问题，它可以有效地安排生产计划，缩短完成时间，解决运输问题和使用最少的资源安排或发展任务。

总的来说，运筹学的应用被广泛用于各种类型的组织和行业中，以改进质量管理，提
高生产效率，改进货物运输效率，以及建立数字化解决方案以及完善视觉决策系统等等。

随着科技的发展，运筹学应用将进一步发挥其重要作用，为组织制定有效的解决方案，应
对复杂的现实问题。

运筹学经典案例
运筹学是一门研究如何有效地组织、管理和优化资源的学科，它在现代管理中
起着至关重要的作用。

在实际应用中，我们可以通过一些经典案例来了解运筹学的具体运用，下面就介绍几个经典案例。

第一个案例是关于生产调度的。

在一个工厂中，有多条生产线，每条生产线上
有不同的产品需要生产。

如何合理安排生产顺序，以最大程度地提高生产效率，是一个典型的运筹学问题。

通过运筹学的方法，可以建立数学模型，考虑到各种约束条件，最终得出一个最优的生产调度方案，从而实现生产效率的最大化。

第二个案例是关于物流配送的。

在物流配送中，如何合理规划配送路线，以最
大程度地降低成本，提高配送效率，也是一个典型的运筹学问题。

通过对各种因素的分析和考虑，可以利用运筹学方法建立配送优化模型，从而得出最优的配送路线和方案。

第三个案例是关于库存管理的。

在企业的库存管理中，如何合理控制库存水平，以最大程度地降低库存成本，同时又能够保证供应链的稳定性，也是一个典型的运筹学问题。

通过对需求的预测和供应链的优化，可以利用运筹学方法建立库存管理模型，从而实现库存水平的最优控制。

通过以上几个经典案例的介绍，我们可以看到，运筹学在实际应用中发挥着重
要作用。

通过建立数学模型，考虑各种约束条件，运用运筹学方法进行优化，可以帮助企业提高生产效率，降低成本，提高配送效率，优化供应链，从而实现经济效益的最大化。

总的来说，运筹学经典案例的研究和实践对于企业的管理和运营具有重要的指
导意义。

希望通过对运筹学经典案例的深入学习和研究，可以更好地应用运筹学理论，解决实际管理中的问题，实现企业的可持续发展。

运筹学在实际生活中的应用1. 引言运筹学是一门研究如何做出最佳决策的学科，它结合了数学、统计学和计算机科学的方法，并应用于各种实际生活场景中。

本文将探讨运筹学在实际生活中的应用，并介绍一些具体的例子。

2. 资源分配问题在实际生活中，我们常常面临资源有限的情况，如有限的时间、金钱、人力等。

运筹学可以帮助我们合理地分配这些有限资源，以实现最佳效果。

一个常见的例子是旅行路线规划。

假设你打算在一个城市旅行，但时间有限，你希望能够尽可能的游览更多的景点。

运筹学可以帮助你确定最佳的路线，以最短的时间游览尽可能多的景点。

另一个例子是生产计划。

在一个工厂中，有限的生产资源需要合理安排，以满足订单需求。

运筹学可以帮助制定最佳的生产计划，以最小的成本满足订单需求。

3. 供应链管理供应链管理是指对供应链中的各个环节进行有效管理，以优化整个供应链的效率和效益。

运筹学在供应链管理中发挥了重要作用。

一个典型的例子是库存管理。

在供应链中，库存是一个关键的环节。

运筹学可以帮助企业确定最佳的库存策略，以确保库存水平能够满足需求，同时最小化库存成本。

另一个例子是运输优化。

在物流领域，如何合理安排运输路线、调度车辆，以及优化运输成本是一个常见的问题。

运筹学可以帮助制定最佳的运输方案，以降低物流成本并提高运输效率。

4. 项目管理项目管理是指对项目进行有效规划、组织、指导和控制，以实现项目目标的过程。

运筹学在项目管理中的应用也非常广泛。

一个例子是资源调度。

在一个项目中，不同的任务需要不同的资源支持。

运筹学可以帮助项目经理合理调度资源，以确保项目能够按时完成，同时最小化资源浪费。

另一个例子是时间管理。

在项目管理中，时间是一个关键的限制因素。

运筹学可以帮助项目经理制定最佳的项目进度计划，以最短的时间完成项目。

5. 股票投资决策股票投资是一个风险较高的活动，投资者需要在不确定的市场环境中做出决策。

运筹学可以帮助投资者制定投资策略，以降低风险和提高回报。

如下图A、B、C、D、E、F分别表达陆地和岛屿，若河旳两岸 分别被敌对两方部队占领，问至少切断哪几座桥梁才干阻止对 方部队过河？
A
B
C
D
E
F
陆地、河流及桥梁示意图
解：
将A，B，C，D，E，F分别用一种点表达，相互之间有桥相连 旳连一条弧；弧旳容量就是两点间旳桥梁数；设一种方向，得 到网络图如下：
A
例3.设备更新问题
某单位使用一台生产设备，在每年年底，单位领导都要决 策下年度是购置新设备还是继续使用旧设备。
若购置新设备，需要支付一笔购置费；假如继续使用旧旳， 则要支付一定旳维修费用。
一般说来，维修费随设备使用年限旳延长而增长。根据以 往旳统计资料，已经估算出设备在各年年初旳价格和不同 使用年限旳年维修费用，分别示于表1和表2。
相应旳开门方案如图所 示，共开10个门。
B C IJ
H
A
D GK
E
F
开门方案
例5：选址问题
有六个居民点v1，v2，v3，v4，v5，v6，拟定建一夜校，已知 各点参加学习旳人数为25、20、30、10、35、45人，其道路 如图所示，试拟定学校位于哪一种居民点，才干使学习者 所走旳总旅程至少？（图中边旁旳数字为路段长度）
用一条边把代表这两个项目
v2
旳顶点连接起来。这么得到
v3
下图
v1
为了处理这个问题，只需
找到一条包括全部顶点旳
v4
初等链。
v5
如：{v4，v1，v2，v3，v5}是一条初等链，相应旳比赛是： 100m自由泳，50m仰泳，50m蛙泳，100m碟泳，200m自由泳。
此问题旳方案不唯一。
例 2.线路铺设问题
0 50 150 175 200 275 40 0 80 100 120 180 180 120 0 30 60 150 D= 70 50 10 0 10 40 280 210 70 35 0 105 495 405 225 180 135 0

运筹案例分析总结案例背景运筹是一门涵盖了多个领域的学科，它通过数学建模与算法等方法，以优化问题为核心，研究如何在资源有限的情况下，使得系统能够达到最优的效果。

在实际应用中，运筹帮助企业和组织解决了众多复杂的问题，提高了效率、降低了成本。

本文将对几个运筹案例进行分析，并总结出一些关键点和经验教训。

案例一：生产计划优化公司在某次生产计划中遇到了一个问题，他们需要制定一个最优的生产计划，以便在资源有限的情况下提高产能，并同时满足客户的交货期要求。

为了解决这个问题，他们采用了运筹相关的方法。

方法与结果首先，他们对生产流程进行了详细的分析，找出了瓶颈环节和关键资源。

然后，他们使用数学建模的方法，将生产计划问题转化为一个线性规划问题，并使用了相应的算法进行求解。

通过优化生产计划，他们成功地提高了产能，并在满足客户需求的前提下，降低了生产成本。

教训与经验这个案例告诉我们，在处理生产计划优化问题时，我们需要充分了解整个生产流程，找出关键环节和资源瓶颈。

在数学建模和算法选择方面，我们需要选择合适的模型和算法，以求得最优解。

案例二：物流配送路径优化一家物流公司面临一个配送路径优化的问题。

他们需要确定一条最优的配送路径，以减少行驶距离，提高效率，并保证货物能够准时送达目的地。

方法与结果他们采用了运筹中的启发式算法和近似算法来优化配送路径。

首先，他们利用GIS地理信息系统采集了物流网络的数据，并进行了预处理和清洗。

然后，他们使用模拟退火算法和遗传算法等方法，对物流配送路线进行了求解。

通过优化配送路线，他们成功地减少了行驶距离，提高了效率，并准时送达了货物。

教训与经验通过这个案例我们学到，在处理物流配送问题时，使用GIS地理信息系统是非常有帮助的。

此外，启发式算法和近似算法在求解大规模配送路径问题时也非常有效。

然而，我们需要注意算法的参数调优和收敛性的检验，以求得较好的结果。

案例三：投资组合优化一家投资公司面临一个投资组合优化的问题。

运筹学案例的分析一、案例背景介绍本案例涉及一家制造业公司，该公司生产和销售汽车零部件。

由于市场竞争激烈，公司面临着多个挑战，如供应链管理、生产调度和库存管理等方面存在问题。

为了解决这些问题，公司决定运用运筹学方法进行分析和优化。

二、问题分析1. 供应链管理问题公司的供应链管理存在一些瓶颈，如供应商选择、物流运输和库存管理等方面存在问题。

如何优化供应链，降低成本，提高效率是一个亟待解决的问题。

2. 生产调度问题公司的生产线存在一些瓶颈，导致生产效率低下和交货周期延长。

如何优化生产调度，提高生产效率，缩短交货周期是公司急需解决的问题。

3. 库存管理问题公司面临着库存管理方面的挑战，如库存过高、库存周转率低等问题。

如何优化库存管理，降低库存成本，提高库存周转率是公司亟需解决的问题。

三、运筹学方法的应用为了解决上述问题，公司决定运用运筹学方法进行分析和优化。

具体应用如下：1. 供应链管理优化通过对供应链进行建模和分析，确定关键节点和瓶颈环节，优化供应商选择和物流运输方案，以降低成本和提高效率。

同时，建立合理的库存管理模型，通过合理的库存控制策略，降低库存成本，提高库存周转率。

2. 生产调度优化通过对生产线进行建模和分析，确定生产瓶颈和瓶颈环节，优化生产调度方案，提高生产效率和缩短交货周期。

同时，建立合理的生产计划和排程模型，通过合理的生产计划和排程策略，提高生产效率和减少交货周期。

3. 库存管理优化通过对库存管理进行建模和分析，确定库存管理的关键指标和影响因素，优化库存管理策略，降低库存成本和提高库存周转率。

同时，建立合理的库存控制模型和库存管理系统，通过合理的库存控制和管理策略，降低库存成本和提高库存周转率。

四、数据分析和模型建立为了进行运筹学分析和优化，公司需要收集相关的数据，并建立相应的模型。

数据可以包括供应链的各个环节的成本、时间和效率等指标，生产线的各个环节的生产能力和效率等指标，以及库存管理的各个环节的库存成本和库存周转率等指标。

食油生产问题（案例一）分析报告一、模型构造1.1 变量设置设两种硬质油代号分别为HD1、HD2（HD代表Hard）,三种软质油代号分别为SF1、SF2、SF3（SF代表Soft）。

每种油的采购（Buy）、耗用（Use）和储存（Store）量分别在油品的代号前加B、U和S表示。

1—6月份5种油品的采购、耗用和储存量分别在油品代号后面加1—6表示。

总产量用PROD（Product）表示。

第一种硬质油六个月的采购量、耗用量、月末储存量共有17变量，其中，六月末的存储量为500吨。

BHD11，BHD12，BHD13，BHD14，BHD15，BHD16；UHD11，UHD12，UHD13，UHD14，UHD15，UHD16；SHD11，SHD12，SHD13，SHD14，SHD15；第二种硬质油六个月的采购量、耗用量、月末储存量共有17变量，其中，六月末的存储量为500吨。

BHD21，BHD22，BHD23，BHD24，BHD25，BHD26；UHD21，UHD22，UHD23，UHD24，UHD25，UHD26；SHD21，SHD22，SHD23，SHD24，SHD25；第一种软质油六个月的采购量、耗用量、月末储存量共有17变量，其中，六月末的存储量为500吨。

BSF11，BSF12，BSF13，BSF14，BSF15，BSF16；USF11，USF12，USF13，USF14，USF15，USF16；SSF11，SSF12，SSF13，SSF14，SSF15；第二种软质油六个月的采购量、耗用量、月末储存量共有17变量，其中，六月末的存储量为500吨。

BSF21，BSF22，BSF23，BSF24，BSF25，BSF26；USF21，USF22，USF23，USF24，USF25，USF26；SSF21，SSF22，SSF23，SSF24，SSF25；第三种软质油六个月的采购量、耗用量、月末储存量共有17变量，其中，六月末的存储量为500吨。