一位随机数发生器

一位硬件随机数发生器的设计与仿真周新淳【摘要】This paper presents a random number generating circuit , It can generate a random decimal number.The circuit is composed of a switching circuit, a pulse generating circuit, a counting circuit and a display e common chip design , The design has the characteristics of convenience , reliability and low cost. And using simulation software for data statistics. The computer simulation results show that the design implements generator of random number from 0 to 9.%文中设计了一种随机数发生电路,可以生成一位十进制随机数,电路分为开关电路、脉冲产生电路、计数电路和显示电路,采用常用芯片设计,产品方便可靠,成本低廉.并利用仿真软件进行数据统计,仿真结果表明该电路可以有效实现随机产生数码0到9的功能.【期刊名称】《电子设计工程》【年(卷),期】2017(025)006【总页数】4页(P19-22)【关键词】随机数;硬件电路;Multisim;仿真【作者】周新淳【作者单位】宝鸡文理学院陕西宝鸡 721016【正文语种】中文【中图分类】TN709现代生活对随机数的依赖越来越多，比如彩票摇号，车牌摇号，抽取幸运观众等等。

很多地方要求有使用方便、安全快捷的随机数产生方法。

当前主流的随机数电路分为两种，软件型和硬件型。

软件型的随机数产生电路方便快捷，但是安全性不高，而且必须借助电脑运行，在一些重要场合往往不方便使用，而且有安全漏洞。

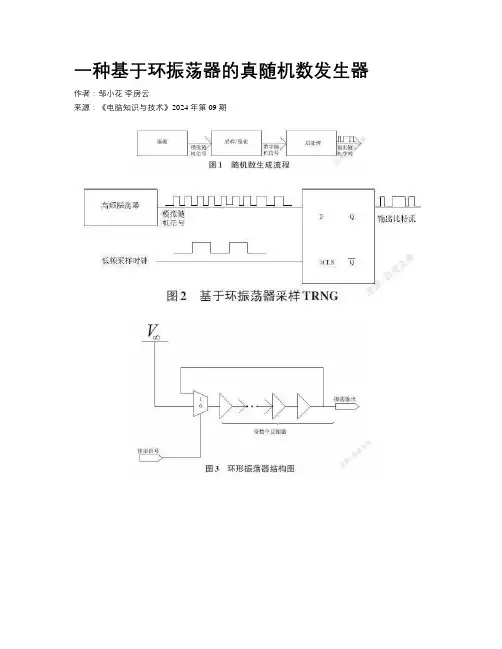
一种基于环振荡器的真随机数发生器作者：邹小花李房云来源：《电脑知识与技术》2024年第09期摘要：真随机数发生器（TRNG）是一种用于生成真随机数的设备，是安全芯片中的重要单元之一，生成的真随机数是确保通信加密及身份认证等密码协议安全性的必要工具。

仿真实验结果表明，随着抖动源抖动程度的增大，每次采样的熵趋近于1，即使在最坏的情况下也能达到误差低于10-4的水平。

文章进一步分析环振荡器（RO）的数学模型并提出一种基于环振荡器的高效率、低成本的真随机数发生器。

关键词：真随机数发生器；TRNG；环振荡器；RO；抖动源；jitter中图分类号：TN79，TN918 文献标识码：A文章编号：1009-3044（2024）09-0008-04开放科学（资源服务）标识码（OSID）0 引言随机数在现实世界中有广泛的应用，比如保障互联网安全的各种加密算法、计算机仿真、电子游戏、抽签等方面。

随机数分为两种，伪随机数和真随机数。

伪随机数是以数论和计算机理论为基础生成的，实现方便、分布均匀、成本低。

由于存在有限的可计算状态，伪随机数具有周期性，使其很容易破解[1]。

自然现象或物理过程中的各种随机噪声是真随机数发生器（True Random Number Generator，TRNG）產生随机数的方式。

伪随机数存在的周期性问题的解决方法让序列具有了真正的随机性，根据热噪声、闪烁噪声等随机噪声往往都是不可预测和产生的随机数无规律难破解的特点。

真随机数发生器产生的随机数存在生成速率相对较慢、随机数的统计特性不好、内外部环境影响的问题。

如何设计满足现代加密系统加密需求、具备良好性能的随机数已成为研究的重要问题。

关注熵源的设计和优化非常重要，因为熵源的品质从根本上决定着随机数发生器性能的好坏[2]。

梳理国内外相关研究的现状表明，有些科研人员已经实现了根据不同原理结构设计的真随机数发生器。

国内科研人员如鲁迎春提出基于可配置异步反馈环形振荡器的真随机数发生器，利用与非门和异或门形成可配置的异步反馈环形振荡器，改善熵源的随机性通过增加相位噪声和扩大时间抖动范围来实现[3]。

真随机数发生器的制作方法
要制作一个真随机数发生器，我们需要利用物理过程或现象来
产生随机性。

下面我将从硬件和软件两个方面来介绍制作真随机数
发生器的方法。

硬件方法：
1. 热噪声发生器，利用半导体器件的热噪声来产生随机数。

可
以利用二极管的热噪声或者场效应晶体管的热噪声来作为随机数源。

2. 光电效应，利用光电二极管或者其他光敏器件接收自然光或
其他光源的微弱光信号，并转换为电信号作为随机数源。

3. 核衰变，利用放射性同位素的核衰变过程来产生随机数。

通
过探测放射性同位素衰变事件的时间间隔来获取随机数。

软件方法：
1. 基于环境噪声的随机数生成，通过利用计算机系统的环境噪声，如鼠标移动、键盘敲击、磁盘I/O等，来获取随机数。

2. 基于时间的随机数生成，利用计算机系统的高精度时钟和时
间戳来产生随机数。

3. 基于混沌理论的随机数生成，利用混沌系统的特性，通过迭
代计算产生随机数序列。

无论是硬件方法还是软件方法，都需要经过严格的测试和验证，确保生成的随机数具有均匀分布、独立性和不可预测性。

此外，真
随机数发生器的安全性也是非常重要的，特别是在密码学和安全通
信领域的应用中。

因此，在制作真随机数发生器时，需要考虑到系
统的安全性和可靠性。

随机数发生器电路-回复
随机数发生器电路是一种电子电路，可以生成一系列看似随机的数字。

在数字系统中，随机数是非常有用的，可以用于密码学、模拟和仿真等应用。

常见的随机数发生器电路有以下几种设计方案：
1. 线性反馈移位寄存器（LFSR）：LFSR是一种基于时钟脉冲的电路，通过将寄存器的输出与某些反馈线上的位进行异或运算来生成下一个状态。

由于反馈位置可以是随意的，因此可以生成看似随机的数列。

然而，LFSR实际上是一种伪随机数发生器，可以通过分析其状态迁移图进行预测。

2. 热噪声发生器：热噪声发生器利用电阻器中由于热运动引起的电子随机运动来生成随机信号。

它通常使用一个放大器来放大噪声信号，并通过滤波器进行后处理以去除其他非随机成分。

3. 电子噪声发生器：电子噪声发生器通过电子器件的随机性来生成随机信号。

例如，基于功率二极管的电子噪声发生器利用二极管的热运动产生随机振荡以生成随机信号。

总的来说，随机数发生器电路可以通过利用物理上的随机性来生成随机信号。

然而，对于安全性要求较高的应用，需要采用更加复杂的算法和技术来生成真正的
随机数，以避免被破解。

一维均匀分布随机数序列的产生方法引言：随机数序列主要应用于序列密码（流密码）。

序列密码的强度完全依赖于序列的随机性与不可预测性。

随机数在密码学中也是非常重要的，主要应用于数字签名（如美国数字签名标准中的数字签名算法）、消息认证码（如初始向量）、加密算法（如密钥）、零知识证明、身份认证（如一次性nonce）和众多的密码学协议。

关键词：随机数、随机数序列、均匀分布一、随机数及随机数序列的简介在统计学的不同技术中需要使用随机数，比如在从统计总体中抽取有代表性的样本的时候，或者在将实验动物分配到不同的试验组的过程中，或者在进行蒙特卡罗模拟法计算的时候等等。

产生随机数有多种不同的方法。

这些方法被称为随机数发生器。

随机数最重要的特性是：它所产生的后面的那个数与前面的那个数毫无关系。

随机数序列分为真随机数序列与伪随机数序列，随机数分为真随机数和伪随机数。

真随机数序列从真实世界的自然随机性源产生，办法是找出似乎是随机的事件然后从中提取随机性，如自然界中的抛币。

在计算机中噪音可以选取真实世界的自然随机性，如从计算机时钟寄存器中取得本机的当前系统时间到秒（或微秒）级的数值，测量两次击键的时间间隔，相邻两次鼠标移动的时间间隔以及由计算机硬件报告的鼠标实际位置等。

伪随机数序列用确定的算法产生，不是真正的随机数序列。

伪随机数序列发生器指使用短的真随机数序列（称为种子）x扩展成较长的伪随机数序列y。

在密码学中伪随机数序列的使用大大减少了真随机数序列的使用，但不能完全取代真随机数序列的使用（如种子）。

通常，我们需要的随机数序列应具有非退化性、周期长、相关系数小等优点。

二、一维均匀分布的简介设连续型随机变量X 的分布函数为 F(x)=(x-a)/(b-a)，a ≤x≤b，则称随机变量X 服从[a,b]上的均匀分布，记为X ～U[a ，b]。

若[x1,x2]是[a,b]的任一子区间,则 P{x1≤x≤x2}=(x2-x1)/(b-a)，这表明X 落在[a,b]的子区间内的概率只与子区间长度有关，而与子区间位置无关，因此X 落在[a,b]的长度相等的子区间内的可能性是相等的，所谓的均匀指的就是这种等可能性。

随机数的原理与计算机实现摘要：随机数在计算机网络信息安全中起着至关重要的作用。

本文将对随机数，随机数产生器如何用计算机语言（JAVA ）实现做简要介绍。

Abstract ：Random number in the computer network information security plays a vital role. This will be random numbers, random number generator to use the computer language (JAVA) to achieve a brief introduction.关键字：随机数、计算机网络信息安全、JAVA 、随机数产生器Keyword ：Random numbers, computer network and information security, JAVA, random number generator一、随机数简介什么叫随机数呢？由具有已知分布的总体中抽取简单子样，在蒙特卡罗方法中占有非常重要的地位。

总体和子样的关系，属于一般和个别的关系，或者说属于共性和个性的关系。

由具有已知分布的总体中产生简单子样，就是由简单子样中若干个性近似地反映总体的共性。

随机数是实现由已知分布抽样的基本量，在由已知分布的抽样过程中，将随机数作为已知量，用适当的数学方法可以由它产生具有任意已知分布的简单子样。

在连续型随机变量的分布中，最简单而且最基本的分布是单位均匀分布。

由该分布抽取的简单子样称，随机数序列，其中每一个体称为随机数。

单位均匀分布也称为［0，1］上的均匀分布，其分布密度函数为：分布函数为 ：由于随机数在蒙特卡罗方法中占有极其重要的位置，我们用专门的符号ξ表示。

由随机数序列的定义可知，ξ1，ξ2，…是相互独立且具有相同单位均匀分布的随机数序列。

也就是说，独立性、均匀性是随机数必备的两个特点。

随机数具有非常重要的性质：对于任意自然数s ，由s 个随机数组成的s 维空间上的点（ξn+1，ξn+2，…ξn+s ）在s 维空间的单位立方体G s 上均匀分布，即对任意的a i ，如下等式成立：⎩⎨⎧≤≤=其他,010,1)(x x f ⎪⎩⎪⎨⎧>≤≤<=1,110,0,0)(x x x x x F si a i ,,2,1，10 =≤≤∏=+==≤si ii i n a s i a P 1),,1,( ξ其中P (·)表示事件·发生的概率。

一维均匀分布随机数序列的产生方法引言：随机数序列主要应用于序列密码（流密码）。

序列密码的强度完全依赖于序列的随机性与不可预测性。

随机数在密码学中也是非常重要的，主要应用于数字签名（如美国数字签名标准中的数字签名算法）、消息认证码（如初始向量）、加密算法（如密钥）、零知识证明、身份认证（如一次性nonce）和众多的密码学协议。

关键词：随机数、随机数序列、均匀分布一、随机数及随机数序列的简介在统计学的不同技术中需要使用随机数，比如在从统计总体中抽取有代表性的样本的时候，或者在将实验动物分配到不同的试验组的过程中，或者在进行蒙特卡罗模拟法计算的时候等等。

产生随机数有多种不同的方法。

这些方法被称为随机数发生器。

随机数最重要的特性是：它所产生的后面的那个数与前面的那个数毫无关系。

随机数序列分为真随机数序列与伪随机数序列，随机数分为真随机数和伪随机数。

真随机数序列从真实世界的自然随机性源产生，办法是找出似乎是随机的事件然后从中提取随机性，如自然界中的抛币。

在计算机中噪音可以选取真实世界的自然随机性，如从计算机时钟寄存器中取得本机的当前系统时间到秒（或微秒）级的数值，测量两次击键的时间间隔，相邻两次鼠标移动的时间间隔以及由计算机硬件报告的鼠标实际位置等。

伪随机数序列用确定的算法产生，不是真正的随机数序列。

伪随机数序列发生器指使用短的真随机数序列（称为种子）x扩展成较长的伪随机数序列y。

在密码学中伪随机数序列的使用大大减少了真随机数序列的使用，但不能完全取代真随机数序列的使用（如种子）。

通常，我们需要的随机数序列应具有非退化性、周期长、相关系数小等优点。

二、一维均匀分布的简介设连续型随机变量X 的分布函数为 F(x)=(x-a)/(b-a)，a ≤x≤b，则称随机变量X 服从[a,b]上的均匀分布，记为X ～U[a ，b]。

若[x1,x2]是[a,b]的任一子区间,则 P{x1≤x≤x2}=(x2-x1)/(b-a)，这表明X 落在[a,b]的子区间内的概率只与子区间长度有关，而与子区间位置无关，因此X 落在[a,b]的长度相等的子区间内的可能性是相等的，所谓的均匀指的就是这种等可能性。

随机数发生器后处理方法随机数发生器是计算机科学中常用的工具，用于生成随机数序列。

随机数的生成对于很多领域都有重要的应用，比如密码学、模拟实验和统计分析等。

然而，随机数发生器生成的随机数序列并不是完美的随机性，往往需要经过后处理方法来提高其质量。

本文将介绍几种常见的随机数发生器后处理方法。

1. 线性同余法线性同余法是最简单也是最常见的随机数发生器。

它的原理是通过一系列的计算操作，将一个初始的随机种子转化为一组伪随机数。

然而，线性同余法生成的随机数序列存在周期性和重复性的问题。

为了解决这个问题，可以通过后处理方法来改善随机数序列的质量。

一种常见的后处理方法是使用置乱算法。

置乱算法通过对随机数序列进行重新排序，打乱原有的顺序，从而提高随机性。

常用的置乱算法有Fisher-Yates算法和Knuth洗牌算法。

这些算法可以有效地打乱随机数序列，降低周期性和重复性的问题。

2. 哈希函数哈希函数是一种常见的随机数发生器后处理方法。

哈希函数将一个输入映射为一个固定长度的输出，具有不可逆性和均匀性。

通过将随机数序列作为输入，将其映射为哈希值，可以提高随机数序列的随机性。

常用的哈希函数有MD5、SHA-1和SHA-256等。

这些哈希函数具有良好的随机性和抗碰撞性，可以有效地提高随机数序列的质量。

但需要注意的是，哈希函数的计算复杂度较高，可能会影响生成随机数的速度。

3. 噪声源噪声源是一种物理随机数发生器后处理方法。

噪声源利用物理上的随机过程，比如热噪声、量子噪声和放电噪声等，生成真正的随机数。

这些随机数具有高度的随机性和不可预测性。

常见的噪声源包括热电偶、Zener二极管和放电管等。

通过将噪声源与计算机系统相连，可以生成真正的随机数序列。

然而，使用噪声源需要专门的硬件设备，成本较高，不适用于所有应用场景。

4. 加密算法加密算法是一种常用的随机数发生器后处理方法。

加密算法利用密钥对随机数序列进行加密操作，从而提高随机数的质量和安全性。

随机数生成器原理随机数生成器是计算机科学中非常重要的一个概念，它可以用来产生一系列看似无规律的数字，但实际上却具有一定的规律性。

在计算机编程、密码学、模拟实验等领域，随机数生成器都扮演着至关重要的角色。

那么，随机数生成器的原理是什么呢？随机数生成器的原理主要分为伪随机数生成器和真随机数生成器两种。

首先，我们来看伪随机数生成器。

伪随机数生成器是通过一定的算法，根据一个起始值，计算出一系列的数字。

这些数字看上去是随机的，但实际上是可以被复现的。

伪随机数生成器的核心在于随机种子的选择和算法的设计。

常见的伪随机数生成算法包括线性同余发生器、梅森旋转算法等。

这些算法都可以根据一个种子值，生成一系列的数字。

但是，由于算法本身的局限性，伪随机数生成器并不能产生真正意义上的随机数。

接着，我们来看真随机数生成器。

真随机数生成器是通过利用物理过程来产生随机数的。

常见的真随机数生成器包括基于热噪声、量子效应、大气噪声等。

这些真随机数生成器利用了自然界中的随机性，产生的随机数是真正意义上的随机数，不受任何规律性的约束。

真随机数生成器在密码学、安全通信等领域有着重要的应用，因为它们能够提供高质量的随机数，从而增强系统的安全性。

无论是伪随机数生成器还是真随机数生成器，它们都在计算机科学中扮演着非常重要的角色。

在实际应用中，我们需要根据具体的需求来选择合适的随机数生成器。

如果只是需要一些看似随机的数字，那么伪随机数生成器是一个不错的选择。

但如果需要高质量的随机数，那么真随机数生成器则是更好的选择。

总的来说，随机数生成器的原理涉及到数学、物理等多个领域，它们的设计和实现都需要深入的专业知识。

随机数生成器的选择对于系统的安全性和性能有着直接的影响，因此在实际应用中需要慎重考虑。

希望通过本文的介绍，读者能对随机数生成器的原理有所了解，并在实际应用中做出明智的选择。