下载文档原格式
第三节_格林公式及其应用
格林公式是一个重要的微积分计算工具，用于计算微分方程在给定边
界条件下的解。
它可以用来解决一类非常有用的问题，例如求解复杂的微
分方程组、积分变分形式的物理问题。
此外，格林公式还可以应用于计算
微分函数在任意区间上的有限性以及在一些特定情况下的无穷性。
格林公式的主要思想是，给定边界以及满足一些条件的控制变量，可
以将一个微分方程组的解表示为不同常量的线性组合。
因此，可以通过解
决有限个简单的常系数非齐次线性微分方程来求解更复杂的微分方程组。
其中，常系数非齐次线性微分对应的格林公式是：
y(t) = A*exp(αt) + B*exp(βt)
其中，A、B是常数，α、β是解的根。
这个公式可以用来求解不同
类型的微分方程，包括拉普拉斯方程、伯努利方程、线性齐次微分方程组等。
应用：
1、求解拉普拉斯方程
拉普拉斯方程是一类重要的常微分方程，它可以用来描述物理系统的
传播过程以及电、热等物理场的扩散等现象。
拉普拉斯方程的一般形式为：y"+αy'+βy=f(t)
这里，α、β是常数，f(t)是一个任意函数。
可以用格林公式来求
解这个方程的解：
y(t) = A*exp(αt) + B*exp(-αt) + [1/α]*∫exp(-αt)f(t)dt
其中，A、B是常数，α是解的根。
2、求解伯努利方程。
第三节 格林公式及其应用 ㈠．本课的基本要求掌握格林公式并会运用平面曲线积分与路径无关的条件，会求全微分的原函数 ㈡．本课的重点、难点格林公式、平面上的曲线积分与路径无关的条件为本课重点，求全微分为难点 ㈢．教学内容一．格林公式及其应用微积分基本定理——牛顿-莱布尼兹公式确立了函数f(x)在闭区间上的定积分与它的原函数F(x)在这个区间的端点上的值之间的关系。
相仿的，在平面闭区域D 上的二重积分与沿区域D 的边界曲线L 上的曲线积分之间也有类似的关系。
格林（Green ）公式就是阐明它们之间关系的一个重要公式。
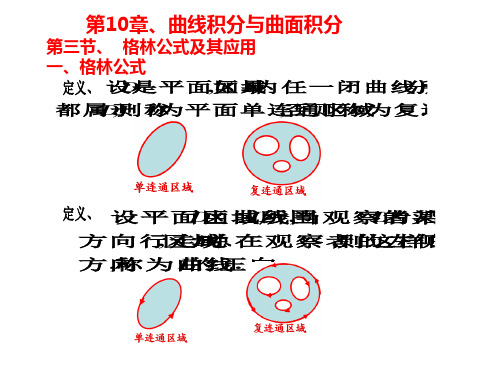
定义（单连通域） 一个平面区域D ，如果全落在此区域内的任何一条封闭曲线都可以不经过D 以外的点而连续地收缩为一点，则称此区域D 为单连通的，否则为复连通的。
（如图） 我们首先规定区域D 的边界曲线L 的正向：当观察者沿L 的某个方向行走时，区域D 总在它的左边（如图），则该方向即为L 的正方向。
定理1（格林定理） 设D 是以分段光滑曲线L 为边界的平面有界闭区域，函数P(x,y)及Q(x,y)在D 上具有一阶连续的偏导数，则⎰⎰⎰+=∂∂-∂∂LQdy Pdx d yPx Q σ)(⑴其中符号⎰L表示沿L 正方向的曲线积分。
公式⑴称为格林公式。
证 先假设穿过区域D 内部且平行坐标轴的直线与D 的边界曲线L 的交点恰好为两点，即区域D 既是X ─型又是Y ─型的情形。
设}),()(|),{(21b x a x y x y x D ≤≤≤≤=ϕϕ。
因为yP∂∂连续，所以由二重积分的计算法有 ⎰⎰⎰⎰⎰-=∂∂=∂∂b a x x b a Ddx x x P x x P dy y y x P dx dxdy y P))}(,())(,({),(12)()(21ϕϕϕϕ 另一方向，由对坐标的曲线积分的性质及计算法有⎰⎰⎰⎰⎰+=+=abbaL L Ldx x x P dx x x P Pdx Pdx Pdx ))(,())(,(2121ϕϕ⎰⎰-=babadx x x P dx x x P ))(,())(,(21ϕϕ因此，=∂∂-⎰⎰Ddxdy y P⎰L Pdx ⑵ 设}),()(|),{(21d y c y x y y x D ≤≤≤≤=ψψ，类似地可证=∂∂⎰⎰Ddxdy x Q⎰LQdy ⑶由于D 既是X ─型又是Y ─型的，⑵、⑶同时成立，合并后即得公式⑴。
