材料力学柴国鈡第10章答案

解： t ≥
pD =
2[σ ]
3×106 ×1 2 × 300×106
= 0.01m = 1.0cm
2
9-8 铸铁圆柱形容器外直径D = 20 cm，壁厚t＝2cm，受内压强p＝4MPa，并在容器两端
受轴向压力P＝200 kN作用，设 µ = 0.25 ，
许用拉应力[σ +]＝25 MPa，（1）用第二强
论作强度校核。 解：
σ
4 xd
=
σ 2 + 3τ 2
σ
= 1202 + 3× 402 = 138MPa < [σ ]
τ
σ τ
题 9-3 图
所以安全。
9-4 某梁在平面弯曲下，已知危险截面上作用有弯矩M＝50.9 kN ⋅ m ，剪力FS＝134.6 kN，截面为No. 22b工字钢，[σ ]＝160 MPa，试根据第三强度理对梁作主应力校核。
σ
m xd
=
σ
1
−
σ σ
+ b − b
σ3
= 1.027 −
256 × (−101.027)
625
=
42.4MPa
9-12 内径为d，壁厚为t的圆筒容器，内部盛有比重为γ ，高度为H的液体，竖直吊装如
图示。试按第三强度理论沿容器器壁的母线绘制圆筒的相当应力σ
3 xd
图（不计端部影响）。
解：
σ
y
=
πd2 4
应力校核。
70
(+)
(−) 30
( Q −图)
(−) 20
(−) 30
24.44 (+)
(M −图)
(−) 20
Wz

= π3 Ed 4 32l 2
4、第四种方式
屈曲形式如解图 d 所示，两杆作为整体绕 z 轴屈曲
µ=2
结构的临界载荷
x FP
x FP
y
O
y
O
习题 10—9 解图 d
7
5、第五种方式
FPcr
= π2 EI z ( µl ) 2
= π2 E ⋅ 2 ⋅ (πd 4
4l 2
64
+ πd 2 4
⋅ ( a )2 2
10－5 正三角形截面压杆，其两端为球铰链约束，加载方 向通过压杆轴线。当载荷超过临界值，压杆发生屈曲时，横截 面将绕哪一根轴转动？现有四种答案，请判断哪一种是正确 的。
（A） 绕 y 轴； （B） 绕通过形心 C 的任意轴； （C） 绕 z 轴； （D） 绕 y 轴或 z 轴。 解：因为过正多边形截面形心的任意轴均为形心主轴，且 惯性矩相等。所以，正确答案是 B。
FAB
cosθ
=
3 cotθ 2
⋅ FP
，
FQ = FP
σ max
=
MB W
+
FNx A
≤ [σ ] ，
0.3FP 185 ×10−8
+
3 2
cot θ
⋅
FP
30.6 ×10−4
≤ 160 ×106 ，
FP ≤ 73.5kN<FPcr = 118kN
所以，托架所能承受的最大载荷为 73.5kN。
10－11 长 l＝50 mm，直径 d＝
习题 10－2 图
解：各杆内力如解图所示，由各受杆内力情况可知，正确答案是 A。
10－3 图中四杆均为圆截面直杆，杆长相同，且均为轴向加载，关于四者临界载荷的大 小，有四种解答，试判断哪一种是正确的（其中弹簧的刚度较大）。

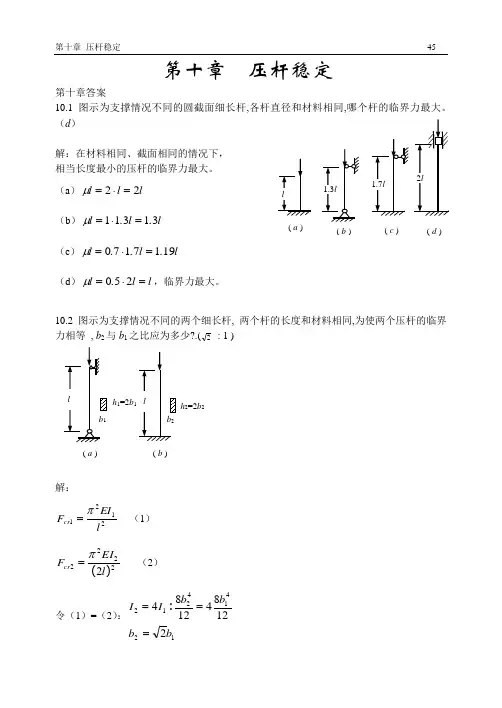
第十章 压杆稳定第十章答案10.1图示为支撑情况不同的圆截面细长杆,各杆直径和材料相同,哪个杆的临界力最大。

（d ）解：在材料相同、截面相同的情况下， 相当长度最小的压杆的临界力最大。

（a ）l l l 22=⋅=μ （b ）l .l .l 31311=⋅=μ （c ）l .l ..l 1917170=⋅=μ（d ）l l .l =⋅=250μ，临界力最大。

10.2图示为支撑情况不同的两个细长杆, 两个杆的长度和材料相同,为使两个压杆的临界力相等 , b 2与b 1之比应为多少?.(2 : 1 )解：2121l EI F cr π=（1）22222)(l EI F cr π=（2）令（1）=（2）：12414212212841284b b b b I I ===:( a)( b) ( c) ( d )( a ) ( b ) h 1=2b h 2=2b 210.3 铰接结构ABC 由截面和材料相同的细长杆组成，若由于杆件在ABC 平面内失稳而引起破坏，试确定荷载F 为最大时(两个杆同时失稳时)的θ (0＜θ＜π/2)角。

(θ=arctan (1/3)=18.44°) 解：θπcos F l EIF cr ==21212)( （1）θπsin F l EIF cr ==22222)( （2）(1/3))(:(2)(1)arctan cos l sin l l l tan ====θθ3130302222110.4图示压杆，型号为20a 工字钢，在xoz 平面内为两端固定，在xoy 平面内为一端固定，一端自由，材料的弹性模量E = 200GPa ，比例极限σp = 200MPa ，试求此压杆的临界力。

(F c r = 402.2kN )解：(1)柔度计算 查表知：6010012158122=-=========bE a ,E.AI i .A I i s p y y zz σλλσπλs 0p 23558mm A mm,mm,(2)xoz 平面内失稳：7894121200050..i l .y ===y λ 为中柔度杆，kN MPa,7048197===-=A F .b a cr cr y cr σλσ （2） (2)xoy 平面内失稳：169858180002..i l Z ===Z λ 为中柔度杆，kN MPa,6901194===-=A F .b a cr cr z cr σλσx10.5 结构如图，二杆的直径均为d =20mm ，材料相同，材料的弹性模量E = 210GPa ， 比例极限σP = 200MPa ，屈服极限 σs = 240MPa ，强度安全系数n =2 ，规定的稳定安全系数n st =2.5 ，试校核结构是否安全。

横截面上的正应力为 FNd ρω 2 D 2 σd = = A 4
12
材 料 力 学 Ⅱ 电 子 教 案
例 10－4 直径d =100 mm的圆轴，右端有重量 P =0.6 kN,直径 － D=400 mm的飞轮，以均匀转速n =1 000 r/min旋转（图a）。在 轴的左端施加制动力偶Md（图b），使其在t＝0.01s内停车。不 计轴的质量。求轴内的最大切应力τdmax。
B
z
A C
1.5m 1.5m
B
z
(a)
(b)
22
材 料 力 学 Ⅱ 电 子 教 案
动荷载·交变应力 第十章 动荷载 交变应力
P h
解：
1. 图a
由型钢查得20b号工字钢的 A Wz和Iz分别为

1.5m 1.5m
B
z
Wz=250×103 mm3，Iz=2 500×104 mm4 梁的最大静应力为
σ st ,max
6
(1) (2) (3)
FN d = K d P
材 料 力 学 Ⅱ 电 子 教 案
钢索横截面上的动应力为
FN d P σd = = K d = K dσ st A A
（4）
式中，σ st =
P 为静应力。 A
由（3）,（4）式可见，动荷载等于动荷载因数与静荷载 的乘积；动应力等于动荷载因数与静应力的乘积。即用动荷因 数反映动荷载的效应。
动荷因数为
2h 2 × 20 = 1+ 1+ = 14.7 ∆st 0.214 3 梁的最大动应力为 Kd = 1 + 1 +
σ d = K dσ st ,max = 14.7 × 6 = 88.2 MPa

第十章 动载荷、选择题1在用能量法计算冲击应力问题时，以下假设中（D ）是不必要的。

A 冲击物的变形很小，可将其视为刚体；B 被冲击物的质量可以忽略，变形是线弹性的；C 冲击过程中只有应变能、势能和动能的变化，无其它能量损失；D 被冲击物只能是杆件。

2•在冲击应力和变形实用计算的能量法中，因不计被冲击物的质量，所以计算结果与实际 情况相比（D ）。

A 冲击应力偏大，冲击变形偏小;B 冲击应力偏小，冲击变形偏大;C 冲击应力和冲击变形均偏大；D 冲击应力和冲击变形均偏小。

3.四种圆柱及其冲击载荷情况如图所示，柱C 上端有一橡胶垫。

其中柱（ 大动应力最大。

IW、计算题1重量为P 的重物从高度H 处自由下落到钢质曲拐上， 试按第三强度准则写出危险点的相 当应力。

D ）内的最解：在C 点作用静载荷P 时，BC 段产生弯曲变形， AB 段产生弯扭组合变形， C 点的静位 移：Pa 3Pl 3 Palstf C f B AB aa 3EI BC 3EI AB GI PAB ’ L 2HK d 1 JV sth 3d 4 d 4式中， I BC， I AB I PAB 12b 64 32危险点在A 截面的上下端，静应力为:.M 2 T 2 P a 2 l 2r3 W Z W Z弹簧支座，重量为 P 250 N 的重物从高度H 50 mm 自由下落到梁的中点C 处。

若铝 合金的弹性模量 E 70 GPa ，试求冲击时梁内的最大正应力。

解：在C 点作用静载荷P 时，AB 梁为静不定问题，变形协调条件为梁中点变形等于弹簧变 形，故有：式中，W Zd 3 32则动应力为：d K d r3 K d P . a 2I 2W Z2、图示横截面为b h 75mm 25mm 的铝合金简支梁，在跨中增加一刚度 K 18 kN/m 的代入数值可计算出：由结构对称，可知R A R B 50 N（资料素材和资料部分来自网络，供参考。

6
w2 = A2 sinkx2 + B2 coskx 2 +
Fc x2 2F
当 x1 = 0，w1 = 0 → B1 = 0 当 x 2 = 0，w2 = 0 → B2 = 0 当 x1 = x2 = 或写成
l F ′ = − w2 ′ ，w1 = w2 = c ，w1 2 c
kl Fc l Fc A1sin 2 + 4 F = c kl Fc l Fc = A2 sin + c 2 4F kl Fc kl Fc A1 kcos 2 + 2 F = − A2 kcos 2 − 2 F
Fc F x1 − Fw1，M ( x 2 ) = c x 2 − Fw2 2 2
′′ + k 2 w1 = w1
式中，
Fc 2 F ′′ + k 2 w2 = c k 2 x2 k x1，w2 2F 2F k2 = F EI
Fc x1 2F
通解为
w1 = A1sinkx1 + B1coskx1 +
式中，
k12 =
以上二微分方程的通解为
F F 2 ，k 2 = EI 1 EI 2
w1 = A1sink1 x1 + B1cosk1 x1 + δ w2 = A2 sink 2 x 2 + B2 cosk 2 x 2 + δ
定未知常数的条件为
′=0 x1 = 0，w1 = 0，w1 x1 = l ′ = w2 ′ ，w1 = w2，w1 x2 = 0 x2 = l，w2 = δ
或简化成
sin
4k 2 EI kl kl kl kl [sin − (1 − )cos ] = 0 2 2 2 2 cl

第10章课后习题答案10-1证明当升角与当量摩擦角符合时，螺纹副具有自锁性。

当时，螺纹副的效率所以具有自锁性的螺纹副用于螺旋传动时，其效率必小于50%。

10-2解由教材表10-1、表10-2查得，粗牙，螺距，中径螺纹升角，细牙，螺距，中径螺纹升角对于相同公称直径的粗牙螺纹和细牙螺纹中，细牙螺纹的升角较小，更易实现自锁。

10-3解查教材表10-1得粗牙螺距中径小径螺纹升角普通螺纹的牙侧角，螺纹间的摩擦系数当量摩擦角拧紧力矩由公式可得预紧力拉应力查教材表9-1得35钢的屈服极限拧紧所产生的拉应力已远远超过了材料的屈服极限，螺栓将损坏。

10-4解（1）升角当量摩擦角工作台稳定上升时的效率：（2）稳定上升时加于螺杆上的力矩（3）螺杆的转速螺杆的功率（4）因，该梯形螺旋副不具有自锁性，欲使工作台在载荷作用下等速下降，需制动装置。

其制动力矩为10-5解查教材表9-1得Q235的屈服极限，查教材表10-6得，当控制预紧力时，取安全系数由许用应力查教材表10-1得的小径由公式得预紧力由题图可知，螺钉个数，取可靠性系数牵曳力10-6解此联接是利用旋转中间零件使两端螺杆受到拉伸,故螺杆受到拉扭组合变形。

查教材表9-1得，拉杆材料Q275的屈服极限，取安全系数，拉杆材料的许用应力所需拉杆最小直径查教材表10-1，选用螺纹（）。

10-7解查教材表9-1得，螺栓35钢的屈服极限，查教材表10-6、10-7得螺栓的许用应力查教材表10-1得，的小径螺栓所能承受的最大预紧力所需的螺栓预紧拉力则施加于杠杆端部作用力的最大值10-8解在横向工作载荷作用下，螺栓杆与孔壁之间无间隙，螺栓杆和被联接件接触表面受到挤压；在联接接合面处螺栓杆则受剪切。

假设螺栓杆与孔壁表面上的压力分布是均匀的，且这种联接的预紧力很小，可不考虑预紧力和螺纹摩擦力矩的影响。

挤压强度验算公式为：其中；为螺栓杆直径。

螺栓杆的剪切强度验算公式其中表示接合面数，本图中接合面数。

计算题10-1、图示矩形截面杆h=200mm ，b=100mm ，P=20KN ，试计算最大正应力。

（cl-xtzj11） 10-2 人字架及承受的载荷如图所示。

试求截面I I -上的最大正应力和a 点的正应力。

10-3 悬臂吊如图所示，起重量（包括电葫芦）G =30kN ，横梁BC 为工字钢，许用应力[σ]=140MPa ，试选择工字钢的型号（可近似按G 行至梁中点位置计算）。

10-4 图示悬臂梁自由端受一与z 轴成ϕ角的横向力P 作用，该力可分解为垂直分力ϕcos P P z =和水平分力ϕsin P P y =。

试据叠加法写出任一截面上任一点K 的正应力计算式，并确定该梁危险点的位置及其应力的计算式。

10-5 斜杆AB 的横截面为100×100mm 2的正方形，若P =3kN ，试求其最大拉应力和最大压应力。

10-6 砖砌烟囱高H =30m ，底截面I I -的外径d 1=3m ，内径d 2=2m ，自重G 1=2000kN ，受q =1kN/m 的风力作用。

试求：（a ）烟囱底截面上的最大压应力。

（b ）若烟囱的基础埋深h =4m ，基础及填土自重按G 2=1000kN 计算，土壤的许用压应力MPa 3.0][=σ，圆形基础的直径D 应为多大？注：计算风力时，可省去烟囱直径的变化，把它看作是等截面的。

10-7 图示一矩形截面杆，用应变片测得杆件上、下表面的轴向应变分别为a ε=1×10-3，b ε=0.4×10-3,材料的弹性模量E =210GPa 。

试绘制横截面的正应力分布图；并求拉力P 及其偏心距e 的数值。

10-8 一矩形截面短柱，受图示偏心压力P 作用，已知许用拉应力[t σ]=30MPa ，许用压应力[c σ]=90MPa ，求许可压力[P ]。

10-9 材料为灰铸铁ＨＴ15-33的压力机框架如图所示。

许用拉应力为[]30=t σMPa ，许用压应力为[]80=c σMPa 。

细心审题
在解题前要认真审题，明确题目要求和解题方向 ，避免出现理解偏差或误解题意的情况。同时， 在解题过程中要细心计算，注意检查计算过程和 结果是否正确。
05 知识点拓展与延伸
相关概念深入理解
材料的力学性能
材料在受到外力作用时，其变形、 破坏以及抵抗变形的能力，包括
弹性、塑性、强度、韧性等。
应力与应变
错误原因剖析
学习态度不认真
部分学生平时学习态度不认真，对课 堂知识掌握不扎实，导致在解题时无 法正确运用所学知识。
缺乏练习
部分学生平时缺乏练习，对解题方法 和技巧不熟悉，导致在考试时无法熟 练应对各种问题。
思维能力不足
部分学生思维能力较弱，无法灵活运 用所学知识解决实际问题。
粗心大意
部分学生在解题过程中粗心大意，忽 略了一些关键信息或步骤，导致解题 错误。
《材料力学》第十章课后习题答案
contents
目录
• 第十章课后习题概览 • 习题解答方法与技巧 • 典型习题详解 • 易错习题剖析及避免方法 • 知识点拓展与延伸 • 自我检测与提高建议
01 第十章课后习题概览
习题类型与数量
选择题
共10道，涵盖基本概念和理论 应用。
填空题
共5道，考查对知识点的理解和 记忆。
典型选择题解析
题目：下列关于剪切应力的说法中， 错误的是？
B. 剪切应力与材料的剪切模量成正比。
A. 剪切应力是相邻两部分材料发生相 对错动时的阻力。
典型选择题解析
C. 剪切应力只存在于受扭转的 杆件中。
D. 剪切应力的方向与材料错动 的方向垂直。
解析：正确答案是C。剪切应力 不仅存在于受扭转的杆件中，还 存在于受剪切的梁、板等构件中。

第十章 组合变形10-2 图a 所示板件，b =20mm ，δ=5mm ，载荷F = 12 kN ，许用应力[σ] = 100 MPa ，试求板边切口的允许深度x 。

题10-2图解：在切口处切取左半段为研究对象（图b ），该处横截面上的轴力与弯矩分别为F F =N(a) )(a b F M −=显然，222xb x b a −=−=(b) 将式(b)代入式(a)，得2FxM =切口段处于弯拉组合受力状态，该处横截面上的最大拉应力为22N max 432(2a)6 22a Fx a F Fx a F W M A F δδδδσ+=+=+=根据强度要求，在极限情况下，][4322σδδ=+a Fx a F 将式(b)与相关数据代入上式，得01039.61277.042=×+−−x x 由此得切口的允许深度为mm 20.5=x10-3 图示矩形截面钢杆，用应变片测得上、下表面的纵向正应变分别为=1.0×10aε-3与=0.4×10b ε-3，材料的弹性模量E =210GPa 。

试绘横截面上的正应力分布图，并求拉力F 及其偏心距e 的数值。

题10-3图解：1.求和a σb σ截面的上、下边缘处均处于单向受力状态，故有MPa84Pa 104.010210 MPa 210Pa 100.1102103939=×××===×××==−−b b a a E εσE εσ偏心拉伸问题，正应力沿截面高度线性变化，据此即可绘出横截面上的正应力分布图，如图10-3所示。

图10-32．求和F e 将F 平移至杆轴线，得Fe M F F ==，N 于是有 a za E εW Fe A F σ=+=E εW Fe AF σzb =−=代入相关数据后，上述方程分别成为26250240=+Fe F 10500240=−Fe F 经联立求解，于是得mm 786.1m 10786.1kN 38.18N 183753=×=≈=−e F ，10-6 图示直径为d 的圆截面铸铁杆，承受偏心距为e 的载荷F 作用。

材料力学柴国钟答案【篇一：材料力学(柴国钟、梁利华)第5章】mmax10?10610?106（a）?1??y1??90?15.4mpa；?2??y2??60?10.3mpa120?1803120?1803iziz12126m10?10?3??maxy3???90??15.4mpa120?1803iz123120?18045?1203（b）iz??2??45360000mm412126mmaxmmax10?1010?106?1??y1??90?19.8mpa；?2??y2??60?13.2mpaiz45360000iz45360000mmax10?106?3??y3???90??19.8mpaiz45360000（c）yc?30?150?75?120?30?165?115mm30?150?120?3030?1503120?30322iz??30?150??115?75???120?30??165?115??24907500mm4 1212mmaxmmax10?10610?106?1??y1??65?26.1mpa；?2??y2??35?14.1mpaiz24907500iz24907500mmax10?106?3??y3???115??46.2mpaiz249075005.2 如图所示，圆截面梁的外伸部分系空心圆截面，轴承a和d可视为铰支座。

试求该轴横截面上的最大正应力。

解：剪力图和弯矩图如下：fsm1.344mb?1.344kn?m，md?0.9kn?m?b,maxmb32mb32?1.344?106????63.4mpa wz?d3??60348?d,maxmd32md32?0.9?106????62.1mpa wz?d31??4??603?1?0.754故，?max?63.4mpa5.3 图示简支梁受均布载荷作用。

已知材料的许用应力[?]=160mpa。

（1）设计实心圆截面的直径d；（2）设计宽度与高度之比b/h=2/3的矩形截面；（3）设计内径与外径之比d/d=3/4的空心圆截面；（4）选择工字形截面的型钢；（5）分析以上4种截面的合理性。

第10章 疲劳强度的概念思考题10-1 什么是交变应力？举例说明。

答 随时间作周期性变化的应力称交变应力。

如下图所示的圆轴以角速度ω匀速转动，轴上一点A 的位置随时间变化，从A 到A ′，再到A ′′，再到A ′′′，又到A 处，如此循环往复。

轴上该点的正应力A σ也从0到，再到0，再到，又到0，产生拉压应力循环。

该点的应力即为交变应力。

+max σ−max σ10-2 疲劳失效有何特点？疲劳失效与静载失效有什么区别？疲劳失效时其断口分成几个区域？是如何形成的？答 （1）疲劳失效时的应力σ远低于危险应力u σ（静载荷下的强度指标）；需要经过一定的应力循环次数；构件（即使是塑性很好的材料）破坏前和破坏时无显著的塑性变形，呈现脆性断裂破坏特征。

（2）疲劳失效的最大工作应力σ远低于危险应力u σ；静载失效的最大工作应力σ为危险应力u σ。

（3）疲劳失效时其断口分成2个区域：光滑区域和颗粒状粗糙区域。

（4）构件在微观上，其内部组织是不均匀的。

在足够大的交变应力下，金属中受力较大或强度较弱的晶粒与晶界上将出现滑移带。

随着应力变化次数的增加，滑移加剧，滑移带开裂形成微观裂纹，简称“微裂纹”。

另外，构件内部初始缺陷或表面刻痕以及应力集中处，都可能最先产生微裂纹。

这些微裂纹便是疲劳失效的起源，简称“疲劳源”。

微裂纹随着应力交变次数的继续增加而不断扩展，形成了裸眼可见的宏观裂纹。

在裂纹的扩展过程中，由于应力交替变化，裂纹两表面的材料时而互相挤压、时而分离，这样就形成了断口表面的光滑区。

宏观裂纹继续扩展，致使构件的承载截面不断被削弱，类似在构件上形成尖锐的“切口”。

这种切口造成的应力集中，使局部区域内的应力达到很大数值。

最终在较低的应力水平下，由于累积损伤，致使构件在某一次载荷作用时突然断裂。

断口表面的颗粒状区域就是这种突然断裂造成的，所以疲劳失效的过程可以理解为裂纹产生、扩展直至构件断裂的一个过程。

10-3 什么是对称循环？什么是脉冲循环？ 答 对称循环是指最大应力与最小应力大小相等，正负号相反的应力循环。

10.1 一端固定一端铰支的工字形截面细长压杆，已知弹性模量GPa 208=E ，截面尺寸200mm×100mm ×7mm ，杆长m l 10=，试确定压杆的临界压力。

解：4337.16796532121869312200100mm I x =⨯-⨯=4332.11719831271861210072mm I y =⨯+⨯=因为x y I I <，故y I I =()()kN N l EI F cr 1.49101.49100007.02.117198310208323222=⨯=⨯⨯⨯⨯==πμπ10.2 两端固定的圆截面钢质压杆，直径为50mm ，受轴向压力F 作用。

已知GPa 210=E 和MPa 200=p σ，试确定能够使用欧拉公式的最短压杆长度l 。

解：8.10120010210505.044322=⨯⨯==≥⨯⨯===πσπλμμλp p E l d l i l可得：mm l 2545≥10.3 截面为矩形h b ⨯的压杆，两端用柱销联接（在y x -平面内弯曲时，可视为两端铰支；在zx -平面内弯曲时，可视为两端固定）。

已知GPa 200=E ，MPa 200=p σ，试求：（1）当mm 30=b ，mm50=h 时，压杆的临界压力；（2）若使压杆在两个平面（y x -和z x -面）内失稳的可能性相同时，求b 和h 的比值。

解：43331250012503012mm bh I z =⨯==，1=z μ，故()()kNN l EI F z z cr 1171011723001312500102003232221=⨯=⨯⨯⨯⨯==πμπ43311250012305012mm hb I y =⨯==，5.0=y μ，故()()kN N l EI F y y cr 1681016823005.0112500102003232222=⨯=⨯⨯⨯⨯==πμπ故kN F cr 117=。

湖北汽车工业学院
材料力学
主讲教师：马迅
第9+10章习题-1、9-2、9-3、9-4、10-2、10-4
附加习题9-2: 1、2杆均为圆截面，直径相同，d=8mm， 材料的E=120GPa，适用欧拉公式的临界柔度为90，规定 稳定性安全系数nst=1.8，求结构的许可载荷P。 解： 应用平衡条件有
PL P l 1
解： yc = ∆ st = 0.0125m
Kd = 1+ 1+
σ st max
M = max = 37.5MPa W
HAII MAXUN
2 × 50 ＝4 ∆ st
( yc ) d = K d ∆ st = 0.05m (σ max ) d = K d σ max = 150MPa
湖北汽车工业学院
材料力学
主讲教师：马迅
在xy平面内弯曲时连杆的柔度
λz = µl 1 × 3.1 = = 59.2 ≈ λ S i z 0.0524
在xz平面内弯曲时连杆的柔度
λy = µl 0.5 × 3.1 = = 61.8 < λ P iy 0.0251
中柔度杆，
Pcr = (a − bλ y ) A = (304 − 1.12 × 61.8) ×106 × 0.00647N = 1520kN
2 9
(
)
P 44500 n = cr = = 2.36 < nst = 2.5 P 18867
工作安全系数小于规定的稳定安全系数，不安全。
HAII MAXUN
附加习题10-2：已知P=300N，L=1m,h=40mm，b=30mm, E=200GPa，计算截面C的冲击挠度和刚架内的最大冲击正 应力（刚架的质量略而不计，不计轴力对变形的影响）。

第十章组合变形的强度计算10-1图示为了梁的各种截面形状,设横向力P的作用线如图示虚线位置,试问哪些为了平面弯曲哪些为了斜弯曲并指出截面上危险点的位置O(a) (b) (c) (d)斜弯曲平面弯曲平面弯曲斜弯曲斜弯曲弯扭组合平面弯曲斜弯曲“x〞为了危险点位置.10-2矩形截面木制简支梁AE 在跨度中点 C 承受一与垂直方向成 =15.的集中力P=10 kN 作用如图示,木材的弹性模量E 1.0 104MPa .试确定①截面上中性轴的解：P y Pcos 10 cos15 9.66 KNP z Psin 10 sin 152.59KN___3750 cm 3W y一_ 3 一 7.25 1031.94甘MPa中性轴:tan 1- tan J y1104tan ------------ tan 155625 25.47f yPyK 339.66 10 348EJ z___ 9 _ 4_ 848 10 10 101020.5434 10 2m位置；②危险截面上的最大正应力；③C 点的总挠度的大小和方向.J z3也竺104 cm 412 W z3310 cmJy1235625 3cmP y l 9.66 3z max44P z l 2.59 3y max44M zmaxM y max103 750 10 61039.84 W y7.25 KN-MM 1.94 KN-MM maxW zf . 0.54342 0.25920.602 cm10-3矩形截面木材悬臂梁受力如图示,P1 = 800 N , P2 = 1600 N . [b ]=10MPa,弹性模量E= 10GPa 设梁截面的宽度 b 与高度h 之比为了1: 2 截面尺寸；②求自由端总挠度的大小和方向.解：(I) M zmaxP 2 1 1.6 KN M ymaxP 0 21.6 KNf zP z l 3 33 2.59 10 348EJ y__一 9_ __ 848 10 105625 10_ 20.259 10 mW zbh 2_2b(2b)2b 33W ybh 2 2b 3材料许用应力O ①试选择梁的方向 中性轴： 25.47max b = 9 cm(II ) ftan M zmax M y maxW z W Y,h = 18 cmP I23 23EJ yf z 1.95匚0.30531.6 102 a-3b31.6 1013bP2 13P2 133EJ z 2EJ z81.11.9710 106._ 210 m 1.97 cm10-4简支梁的受力及横截面尺寸如图示.钢材的许用应力]=160 MPa,试确定梁危险截面中性轴的方向与校核此梁的强度.P=14kN题10-4图解：J z32d4 bh312 321044 6312909.7484cm中性轴:d32bh312 321046 4312949.748 4cmtan 1里tanJ ytan909.748 x _---------- t an 45949.74843.77(mm 的等边角钢,假设 P =25kN,试求最大弯矩截面上 A 、宙日C 点的弯曲正应力.z 10 sin 43.77 6.918 cm y10 cos43.77 7.221cmMmax14 1 14 KNmM y Mmaxcos 45 9.9M zMmaxsin 45 9.9危险点:9.9max103 6.918 10 9.9 8949.748 102107.221 10150.69 MPa8909.748 10J y0 1180.04cm4JZ044554.55cmW z0 322.06cm 3 W y0146.55cm 3pl M max25 KN 4 M y M z M cos45 M zM yA — y A— J zOJ y °146.2MPaM zM yC —V AzJZ OJ y °解: mZ AA 17.68 KN m3317.68 10141.42 10.一 84554.55 1036.42 MPa3317.68 1060.95 1041180.04 1010-5图示简支梁的截面为了精品资料，欢迎大家下载！317.68 103----------------- 8 80.47 10 120.561180.04 1010-6旋臂 式吊车 梁为了16号工字钢,尺寸 如下图,允许 吊重[]=160MPa .试校核吊车梁的强度.解：B 点:No16 工字钢：A 26.1cm 2, J z 1130cm 4H 10-6 图H N H HP 1.08 1.941.94 1.940.8 15.57 KN1.94 - 15.57 37.76 KN 0.8max337.76 10310 1.08 10 A W 26.1 10141 1091.1MPa 压M y L BMPaP =10kN ,材料的,W z 141cm 3[P ],并作危险截面上的应力分布图,指出最大应力发生在哪一点 解：N = P2A 2.5 10 25cm 2N MA WP 120 106?1 60 10 225 10 4 41.667 10d,♦府制I题 10-72M max 60P 10 2, W.22.5 1026_____ 341.667 cm8108N 8.108KN10-8 悬重构架如下图,立柱AB系用No25a的工字钢制成.许用应力[]=160 MPa ③列式表示顶点B的水平位移.解:'一图(II ) max_ _ _3M 20 103W 48.5 10 4153.42MPa一_360 103 6------------------------- 6 153.42 10 Pa401.883 10(III) f B P 9 P 6 --------- 3 9 63EJ 6EJ 117PEJ在构架C点承受载荷A 20kN.①绘立柱AB的内力图；②找出危险截面,校核立柱强度;—图精品资料，欢迎大家下载！B面为了20cm 30cm 的矩形.试求其危险截面上的最大正应力.解： R A 25 2.4/3.6 16.6667 KNN = 25 KN0 10-9 IH10-9图示起重结构,A 及B 处可作皎链支承看待, G D 与E 均用销钉连结.AB 柱的截M max 25 1 03 2.4i^^^x16.667 2.4 10320 KN mA 0.2 0.3 0.06 M 26 0.2 0.32 W ----- 0.003M 2杆的总重 P 及倾角 .试确定自A 点至由于杆自重产生最3斗~ 7.0830.003M Pa10-10有一等直实心圆杆, 其B 端为了皎支承,A 端靠在光滑 的竖直墙面上（摩擦力可略如图示.杆长L,杆截面直径d,N M A W325 10 0.06K 10-8 ffl240c EDm精品资料，欢迎大家下载！大压应力的横截面之距离 S .解：设杆的自重为了 q (N/M) 轴向分量：q sin 横向分量： q cos R A q l cos 2sin1 ql cot在S 截面：NR A cos sin M(s)(R A sin2(qd dscos q sin1 2q cot sinl_ 28 cot 0 l _ 2i tanIql cot cos q 2 S 21 2qsin1ql cot sin cos sincos sin10-11某厂房柱子,受到吊车梁的铅垂轮压 P= 220 kN,屋架传给柱顶的水平力 Q =8 kN ,及风载荷 q= 1kN/m 的作用.P 力作用线离柱的轴线距离 e=,柱子底部截面为了矩形,尺寸为了 试计算柱子底部危险点的应力. N P 220 KN … 1 9 52M max 220 0.4 8 9.5 57.129 2N M 220 103 57.129 103 6A W 1 0.3 0.3 12解： KN m 0.41 1.876MPa2s1q cos S 2■ lO'll RP=22QkN度.解:P Peb A bh26 103一 - _ 3 _ _ 26 6 103 6 10 2_ 42 3 102 32 10 6130 106 Pa 130MPa尺寸单位十mm期10-12图LW 一, ■ ■:A 10-13 图10-13轮船上救生艇的吊杆尺寸及受力情况如图示, 图中载荷班包含救生艇自重及被解：N 18 KNM 18 1.5 27 KN mN M 318 103_ _ 3 27 103A WW 10 4Q160. 7 5救人员重量在内.试求其固定端A-A截面上的最大应力.MPa3210-14正方形截面拉杆受拉力P= 90kN作用,a = 5cm,如在杆的根部挖去1 /4如图示.试求杆内最大拉应力之值.解:2 .2a ——a2形心位置：e --------------2—— 1.179 cm3 a4a 2 2J z 2 a e12 122 2a ——a2364.6 4cm解:1 旦 6Pe E E bh bh 2211 P 6Pe ~ 2- EE bh bh1 2P E bh 1 12Pe E bh 12Pe bh2 6 2P h bhP Pe (V e )90 103maxA —J —3 52 10 4322 5(90 1031.179 10 2)( ------------- 1.179) 10364.6 10 825.72 106Pa 25.72MPa10-15承受偏心拉伸的矩形截面杆如图示, 今用电测法测得该杆上、下两侧面的纵向应变1和2.试证明偏心距e 在与应变1, 2在弹性范围内满足以下关系式10-16图示正方形截面折杆： 外力P 通过A 和B 截面的形心.假设P= 10kN,正方形 截面边长a =60 mm .试求杆内横截面上的最大正应力.解: BC 杆C 截面:AC 杆C 截面:cos8KNM (P cos )0.6 10 0.8——0.6 4.8KN m1N6Mmax3 A a 3N P sin 10 10 M (P cos )0.63 016KN 110 08 0.6 4.8KN m1 max36 1034103------ . ----- 135 106Pa 135MPa 216 10iV10-17试确定图示T字形截面的核心边界.图中y、z两轴为了截面形心主惯轴.解:e yz.i z e zz.i za z a z zi y 60 403 340 9012 1260 40 一 - 一一290 40 458.33cmz .i z _ _ _340 603122302 (40 60)_ _ _ 390 40312_ 2202 (40 90) 60 40 90 40(4)(5)2800cm800e ye ye ze ze ye z2040800cm a z60458.3345458.334580013.33 cm108458.334510.18510.1857.410.185cmcma ze ye ye z 0e y 7.4e z 10.185解:y z y 1 J y 10-18材料为了灰铸铁 HT15— 33的压力机框架如图示.许用拉应力 []=30MPa 许用压应力[]=80 MPa .试校核框架立柱的强度. (2 10) 1 (2 6) 5 (2 5) 9 ------- ------ ------ ------- ------ ---- 4.05cm10 5.95cm 10 23 12(2 ____ 4487.9cmMZ 2T y M z_____Z1云2 A 42cm 10) 3.052312 1042 10 42.86 1062.893 2 6 0.952 12 210 4.05 10 487.9 10 8322.89 10 5.95 108487.9 10已J 10 4.9521226.85MPa32.38MPa10-19电动机功率 4,转速n =800r/m .皮带轮直径 A 250mm 重量 E 700N,皮带拉fig 10-19 图力为了T i, T2 (T i = 2T2),轴的外伸端长L=120mm轴材料的许用应力[ 100MPa试按第四强度理论设计电动机轴的直径d.解:M n T1 T2 D 竺9.55 N n 9.55 8830.1054 KN800T2 2 0.1054 0.843KN0.252 2 3?2cos45 G 3T2 cos45, 3.3 84370023 3432xd3064N3.064KNR l 3.064 0.12M 2 0.75M n2W z2 2M 0.75M n3 3.79 323------------- 3.38cm0.368KN m,'0.3682 0.75 0.10542 106100 1060.379 1010-20直径为了60cm的两个相同皮带轮,n= 100 r /m时传递功率N=, C轮上皮带是水[]=80MPa,试平的,D轮上是铅垂方向的.皮带拉力T2= kN , T1>T2,设轴材料许用应力® 10^20 图根据第三强度理论选择轴的直径,皮带轮的自重略去不计.M B T 1 T 20.25 5.343 0.25 1.336KN m_ 22M D .1.4252 0.4452 1.493KN m一 2_ _ 2 - 226 M D M n . 1.49320.7032 106320.63cm 解:M n R 色 5 0.15 0.75KN mN 7.36M n 9.559.55 —n 100T 1_ D _ T 2 M n20.7029KN m1.52 0.70290.63.843KN80 106 d 3 32W z 3 32 20.635.95cm10-21图示钢制圆轴上有两个齿轮,齿轮 C 上作用着铅垂切向力 P = 5kN,齿轮D 上作解用着水平切向力 P 2 = 10 kN .假设］ :=100 MPa,齿轮C 的节圆直径 d C =30cm 齿轮D 的节圆直径d D= 15cmo 试用第四强度理论选择轴的直径..1.1252 0.187序0.75 0.752 1063 v13125cm3100 106ch 3 32W z 32 13.1255.11cmW z 2 .0.56252 0.3752 0.75 0.752 1 06100 106____ 39.375cm34.57 cm10-22某型水轮机主轴的示意图如下图. 水轮机的输出功率为了NH 37500kW 转速n= 150r /作轴向推力R = 4800kN,转轮重W= 390kN;主轴的内径d= 34cm,外径 A 75cm,自重W=285kN.主轴材料为了45钢,其许用应力为了[]=80 MPa.试按第四强度理论校核主轴的强度.解：37500M n 9.55 2387.5KN m150N P y W c W 4800 390 285 5475KNd23 N 5475 10 15.6A 0.351.2 3 2.15.62 3 30.12 54.4MPa10-23图为了某精密磨床砂轮轴的示意图.电动机功率 4 3 kW转子转速n= 1400 r/m,转子重量Q= 101NL砂轮直径D= 250 mm砂轮重量Q= 275 kN.磨削力P y: P z3:1, 砂轮轴直径d= 50m,材料为了轴承钢,[]=60MPa (1)试用单元体表示出危险点的应力解:M n9.55N9.55 0.02046 KN m 20.46N mn 1400DP z M n2P z 2M n 2 20.46163.68NW pD2 d20.7520.342 2------------------ 0.351m2£l a41630~^ 1 0.4534 0.0793m316M nw p32387.5 100.079330.1MPaxd4题10-23图状态,并求出主应力和最大剪应力；( 2)试用第三强度理论校核轴的强度.砂轮P y 3P z 491.04N显然：P y 、P z 、Q i 和Q 2相较均可以忽略不计. 故 M 275 1000 0.13 35750N m11 ax35750 35750 32 - 2913MPa 0.05解：m-m M n P 0.17 50 0.17 8.5KN mM P(160 90) 10 3 12.5KN mn-n: M n P 90 10 3 4.5KN m7KN mmax题10«24图及臂矩形截面 32 .. M n 2 M 2xd 33d328.52 12.52 1060.12389.1MPa10-24曲柄臂尺寸如图示,假设 P= 50 kN, [ : = 90 MPa,试按第三强度理论对 mmn - n 截面进行校核.h 150 a 0.2492.14(b 700.793虹 0 794^__ ab 2h0.249 15 72 10,26.6672 4 19.422 47.11MPa10-25图示传动轴左端伞形齿轮C 上所受的轴向力 R=kN ,周向力P 2=,径向力 R=.右端齿轮D 上所受的周向力P 2' 144.9kN ,径向力P 3' 52.8kN ,假设d =8cm, [ ]=300MPa, 试按第四强度理论对轴进行校核.M W Z7 103 7 15226.667MPa10解:19.42MPaxd 3M max12.17162 N M max_24.43522316.5 10312.95KN m 312.59 103maxA W z20.082 一一30.083432M n M p3.283 257.63 260.92MPa4xd3.913 103 —0.083 1638.92MPa260.922 3 38.922 269.48MPa10-26正方形截面的半圆形杆,一端固定一端自由,作用力垂直干半圆平面.其受力和尺寸如下图.试按第三强度理论求 B 、C 截面上危险点的相当应力.以上资料仅供参考，如有侵权，留言删除！B 0_l /\l t 7cxl t n cxl r cxl CXI e p xS I A I CXI r:OL9E LD寸£君.6008 N pxE 09L 9ln r co 80CXI .0%艺SIAI 91000OL9L9IO 乜cxll .o osdlAI寸寸寸05SIAI9N §E N X CXI O CXI Ob-E Nxz.0 BO10, 6 64 133.3 10 135.6 10 Pa 135.6MPa36 10 4以上资料仅供参考，如有侵权，留言删除！。

材料力学王博马红艳第十章答案详解1.什么是疲劳极限？试件的疲劳极限与构件的疲劳极限有什么区别和联系？答：疲劳极限（也叫持久极限）是指对光滑小试件进行交变应力循环试验，经过无穷多次应力循环而不发生破坏的最大应力值的最高限值。

试件的疲劳极限是用光滑小试件在实验室条件下，排除工程构件中的应力集中、构件尺寸以及表面加工质量等因素的影响后得到的。

要确定工程实际构件的疲劳极限，必须考虑这些实际因素的影响。

2.影响疲劳极限的主要因素是什么？答（1）构件外形（应力集中）（2）构件尺寸；（3）表面加工（包括表面处理）质量：3.“疲劳失效是材料长期使用后，因疲劳而引起材质脆化的结果。

”这种说法对吗？为什么？答：疲劳失效不是材料长期使用疲劳而引起材质脆化的结果。

疲劳失效的过程可以理解为裂纹产生、扩展直至构件断裂的一个过程。

4.柴油发动机连杆大头螺钉在工作时受到的最大拉力kN=F，最小拉力。

螺纹处内径。

求其平均应力kN =F mm =d m o，应力幅a o，循环特征r。

解最大应力MPa 561Pa1T466232max max max =×=××××===?d F AFo最小应力MPa 537PaTT466232min min min =x=××××===?d F AFo平均应力()()MPa121min max m =+×=+=5ao应力幅度()()MPa121min max a =?x=?=oao循环特征537max min ===oor其t ?o曲线如图所示。