动力学中的简谐振动与振幅频率关系

高二物理简谐振动 振幅、周期、频率 知识精讲 人教版一. 本周教学内容：第九章 第一节 简谐振动 第二节 振幅、周期、频率二. 知识要点：知道什么是简谐运动以与物体做简谐运动回复力特点，理解位移和回复力的概念，理解简谐运动在一次全振动中位移、回复力、加速度和速度的变化情况。

理解弹簧振子概念与实际物体运动抽象为弹簧振子的条件。

理解回复力kx F -=的意义。

知道振幅、周期、频率是描述振动整体特征的物理量，知道它们的物理意义，理解振幅和位移的区别，理解周期和频率的关系，知道什么是固有周期和固有频率。

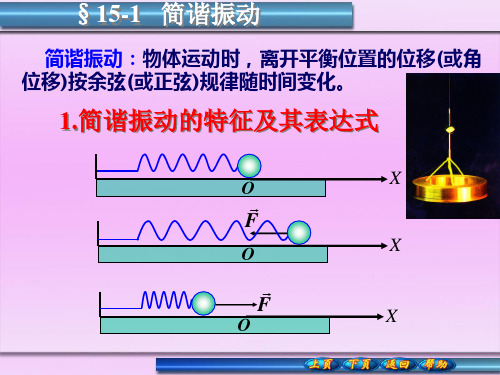
三. 重点、难点解析： 1. 机械振动：物体〔或物体的一局部〕在某一位置附近做往复运动，叫做机械振动，简称振动。

物体受力满足2条才能做振动①是每当物体离开振动的中心位置就受到回复力作用力；②是运动中其它阻力足够小。

描述振动的名词。

① 平衡位置：物体振动停止时的位置也就是静止平衡的位置。

② 回复力：振动物体离开平衡位置就受到一个指向平衡位置的力，叫回复力。

回复力是力的作用效果命名的。

它可以是一个力，也可以是某个力的分力或者几个力的合力。

只要物体离开平衡位置回复力就不为零，方向指向平衡位置。

③ 振动位移：以平衡位置为原点〔起点〕的位移。

数值为从平衡到振动物体达到的位置的直线距离方向由平衡位置指向物体位置。

④ 一次全振动：物体以一样的速度经某位置，又以一样的速度回到同一位置，叫完成一次全振动。

2. 简谐振动：① 弹簧振子：一轻弹簧连接一质点，质点运动时不受摩擦阻力。

这样的装置叫弹簧振子。

弹簧振子沿水平方向运动过程分析，取水平坐标轴，平衡位置为原点。

弹簧处原长状③ 回复力：kx F -=。

④ 简谐运动的定义：质点在跟偏离平衡位置的位移成正比，并总指向平衡位置的回复力作用下的振动叫简谐运动。

⑤ 简谐运动的动力学特征：kx F -=。

⑥ 运动学特征：x mka -=是变加速运动。

⑦ 整体特征与运动学量变化规律：位移、加速度、速度都按周期性变化。

简谐运动、简谐波一、基本概念原理1、振幅：物体离开平衡位置的最大距离，叫做振动的振幅。

用字母A 表示。

振幅是标量。

振幅是表示振动强弱的物理量。

2、周期：做简谐运动的物体完成一次全振动所需要的时间，叫做振动的周期。

用字母T 表示。

频率：单位时间内完成全振动的次数，叫做振动的频率，用字母f 表示。

周期和频率都是表示振动快慢的物理量，周期越短，频率越大，表示振动越快。

周期与频率的关系：T f 1，频率的单位是赫兹，符号是Hz 。

3、简谐运动的对称性在图中，O 点为振动的平衡位置，M 、N 点为最大位移处，OA=OB ，即A 与B 关于O 点对称。

讨论得出以下结论： （1）物体通过A 、B 点时的速率相等。

在A 、B 点弹簧的形变量相等，弹簧的弹性势能相等，则振子的动能相等。

（2）振子运动过程中，A →O 、O →B 、B →O 、O →A 时间相等；M →A 、B →N 、N →B 、A →M 时间相等。

因此，A →O →B →N →B 的运动时间等于半个周期。

（3）在一个周期内，振子通过的路程等于4A ，振子的位移为0。

在半个周期内，振子通过的路程等于2A ，振子的位移大小在0～2A 间。

在1/4周期内，振子通过的路程可能大于A ，也可能小于A 。

讨论：如图，D 为ON 的中点，由于在OD 段的速度大于在DN段的速度，因此，t OD > t DN ，即t OD <T/8，t DN > T/8。

D →N →D 的时间大于T/4，路程等于A ，D →O →C 的时间小于T/4，路程等于A 。

这就说明，在1/4周期内，振子通过的路程可能大于A ，也可能小于A 。

4、运动过程分析确定图中小球在各个位置所受的合外力和位移（已知：OB=BC=5cm ；OA=OD=10cm ，小球与一弹簧连在一起，k=100N ／m ， O 点为弹簧原长）位移和力的关系分析：小结：简谐运动的受力特点：回复力的大小与位移成正比，回复力的方向指向平衡位置。

机械振动和机械波考点例析一、夯实基础知识1、深刻理解简谐运动、振幅、周期和频率的概念（1）简谐运动：物体在跟偏离平衡位置的位移大小成正比，并且总指向平衡位置的回复力的作用下的振动。

特征是：F=-kx,a=-kx/m（2）简谐运动的规律：○1在平衡位置： 速度最大、动能最大、动量最大；位移最小、回复力最小、加速度最小。

○2在离开平衡位置最远时： 速度最小、动能最小、动量最小；位移最大、回复力最大、加速度最大。

○3振动中的位移x 都是以平衡位置为起点的，方向从平衡位置指向末位置，大小为这两位置间的直线距离。

加速度与回复力、位移的变化一致,在两个“端点”最大，在平衡位置为零，方向总是指向平衡位置。

（3）振幅A ：振动物体离开平衡位置的最大距离称为振幅。

它是描述振动强弱的物理量。

它是标量。

（4）周期T 和频率f ：振动物体完成一次全振动所需的时间称为周期T,它是标量，单位是秒；单位时间内完成的全振动的次数称为振动频率，单位是赫兹（Hz ）。

周期和频率都是描述振动快慢的物理量，它们的关系是：T=1/f.2、深刻理解单摆的概念(1)单摆的概念：在细线的一端拴一个小球，另一端固定在悬点上，线的伸缩和质量可忽略，线长远大于球的直径，这样的装置叫单摆。

(2)单摆的特点：○1单摆是实际摆的理想化，是一个理想模型; ○2单摆的等时性，在振幅很小的情况下，单摆的振动周期与振幅、摆球的质量等无关; ○3单摆的回复力由重力沿圆弧方向的分力提供，当最大摆角α<100时，单摆的振动是简谐运动，其振动周期T=gL π2。

(3)单摆的应用：○1计时器；○2测定重力加速度g=224TL π.3、深刻理解受迫振动和共振(1)受迫振动：物体在周期性驱动力作用下的振动，其振动频率和固有频率无关，等于驱动力的频率；受迫振动是等幅振动，振动物体因克服摩擦或其它阻力做功而消耗振动能量刚好由周期性的驱动力做功给予补充，维持其做等幅振动。

(2)共振：○1共振现象：在受迫振动中，驱动力的频率和物体的固有频率相等时，振幅最大，这种现象称为共振。