工程测量第四章角度与距离测量

--角度、距离测量与全站仪的使用方法课件(二)1. 角度测量的方法- 使用经纬仪或者全站仪可以进行角度测量。

- 角度测量需要先进行基准线的设置，然后通过望远镜观察目标点并记录下角度数值。

- 在进行角度测量时，需要注意仪器的稳定性，避免因为仪器晃动或者不平稳导致测量结果不准确。

2. 距离测量的方法- 距离测量可以使用测距仪或者全站仪进行。

- 在使用测距仪进行测量时，需要先设置基准线，然后通过测距仪测量目标点与基准线的距离，并记录下数值。

- 在使用全站仪进行测量时，可以通过激光测距的方式进行，需要先设置基准线，然后通过激光测距仪测量目标点与基准线的距离，并记录下数值。

3. 全站仪的使用方法- 全站仪可以同时进行角度和距离的测量，具有高精度和高效率的优点。

- 在使用全站仪进行测量时，需要先进行基准线的设置，然后通过望远镜观察目标点并记录下角度数值，同时通过激光测距仪测量目标点与基准线的距离。

- 在进行全站仪测量时，需要注意仪器的稳定性和准确性，避免因为仪器晃动或者误差导致测量结果不准确。

4. 角度、距离测量的应用- 角度、距离测量在建筑、道路、桥梁等工程领域中具有广泛的应用。

- 通过角度、距离测量可以确定地面的高度、长度、宽度等参数，帮助工程师进行规划和设计。

- 在地理勘探和地图制作中，角度、距离测量也是必不可少的工具。

5. 注意事项- 在进行角度、距离测量时，需要保持仪器的稳定性和准确性，避免因为误差导致测量结果不准确。

- 在进行测量前，需要进行基准线的设置，避免因为基准线的不准确导致测量结果不准确。

- 在进行全站仪测量时，需要注意仪器的校准和维护，避免因为仪器的故障导致测量结果不准确。

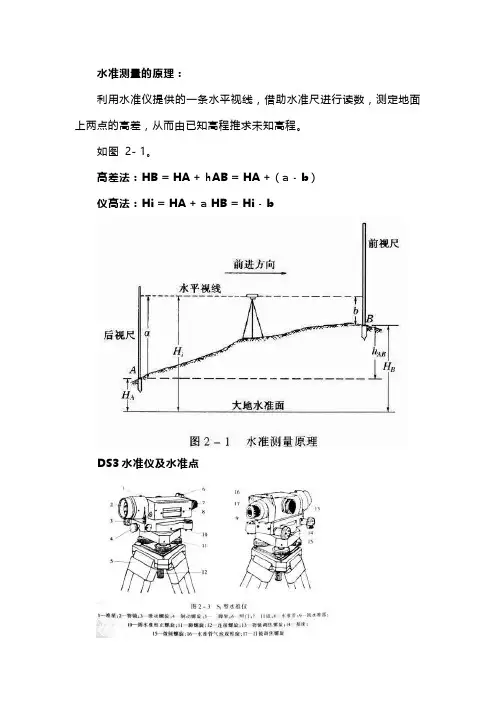
水准测量的原理：利用水准仪提供的一条水平视线，借助水准尺进行读数，测定地面上两点的高差，从而由已知高程推求未知高程。

如图2- 1。

高差法：HB = HA + hAB = HA + ( a - b )仪高法：Hi = HA + a HB = Hi - bDS3水准仪及水准点水平角测量原理（一）定义：水平角就是地面上某点到两目标的方向线铅垂投影到水平面上所成的角度，其取值范围为0 ~ 360。

（二）测角原理：如图3-1测回法测回法是测水平角的基本方法，用于两个目标方向之间的水平角的观测。

如图，设O为测站点，A、B为观测目标，用测回法观测OA与OB两方向之间的水平角β。

竖直角测量原理：（一）定义地面某点至目标的方向线与水平面之间的夹角，取值范围为–90~90。

仰角为正，俯角为负。

（二）测角原理：如图距离：两标志点之间的水平直线长度。

直线定线：把多根标杆标定在已知直线的工作。

方法有目估定线和经纬仪定线。

钢尺量距：精密钢尺量距时必须对所量距离施加尺长改正、温度改正，倾斜，即用钢尺的实际长度。

其实际长度用尺长方程式表示，它的一般形式为：l t = l + Δl + a ×l（t - t0 ）视距测量：利用望远镜的视距丝装置，根据几何光学原理同时测定距离和高差的方法。

视线水平时：距离：D = k·l 高差：h = i –v斜距情况下：距离：D = kl cos2α高差：h = ( 1 / 2 ) kl sin2α+ i –v式中：l为上下丝读数之差；α为竖直角；i为仪器高；v为目标高（中丝读数）；k = 100光电测距：原理：通过测定光波在两点间传播的时间计算距离的方法。

公式：D′= ( 1 / 2 )* c* t式中：c为空气中的光速；t为光波在两点间往返的时间。

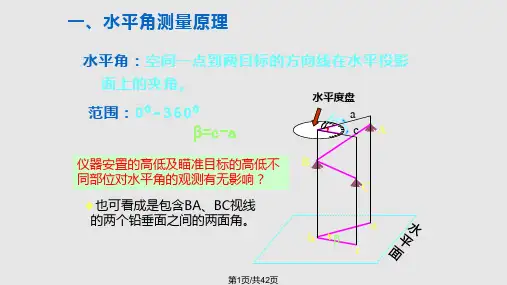
第四章全站仪角度测量、距离测量、高程测量第一节角度测量3.1 角度测量原理水平角测量原理水平角：是指地面上一点到两个目标点的连线在水平面上投影的夹角，或者说水平角是过两条方向线的铅垂面所夹的两面角。

如图，β角就是从地面点B到目标点A、C所形成水平角，B点也称为测站点。

水平角的取值范围是从的闭区间。

那么我们如何测得水平角β的大小呢？我们可以想象，在B点的上方水平安置一个有分划（或者说有刻度）的圆盘，圆盘的中心刚好在过B点的铅垂线上。

然后在圆盘的上方安装一个望远镜，望远镜能够在水平面内和铅垂面内旋转，这样就可以瞄准不同方向和不同高度的目标。

另外为了测出水平角的大小，因此还要有一个用于读数的指标，当望远镜转动的时候指标也一起转动。

当望远镜瞄准A点的时候，指标就指向水平圆盘上的分划a，当望远镜瞄准C点的时候，指标就指向水平圆盘上的分划c，假如圆盘的分划是顺时针的，则水平角β＝c-a竖直角测量原理竖直角：在同一竖直平面内，目标方向线与水平方向线之间的夹角成为竖直角。

当目标方向线高于水平方向线时，称仰角，取正号，反之为俯角，取负号。

竖直角取值范围。

那么如何测竖直角呢？我们可以想象在过测站与目标的方向线的竖直面内竖直安置一个有分划的圆盘，同样为了瞄准目标也需要一个望远镜，望远镜与竖直的圆盘固连在一起，当望远镜在竖直面内转动时，也会带动圆盘一起转动。

为了能够读数还需要一个指标，指标并不随望远镜转动。

当望远镜视线水平的时候，指标会指向竖直圆盘上某一个固定的分划，如90 （如小图）。

当望远镜瞄准目标时，竖直圆盘随望远镜一起转动，指标指向圆盘上的另一个分划。

则这两个分划之间的差值就是我们要测量的竖直角。

根据水平角和竖直角测量原理，要制造一台既能够观测水平角又能观测竖直角的仪器，它必须要满足几个必要条件：1.仪器的中心必须位于过测站点的铅垂线上。

2.照准部设备（望远镜）要能上下、左右转动，上下转动时所形成的是竖直面。

3.要具有能安臵成水平位臵和竖直位臵并有刻划的圆盘。

第四章角度测量与距离测量第一节角度测量原理地面点的平面位置，往往通过测定水平角度和丈量距离来计算坐标。

该点的高程，除了用水准测量方法确定外，还可以通过测定竖直角用三角高程测量方法确定。

因此，测定水平角和竖直角都是测量的基本工作，统称为角度测量。

一、水平角测量原理水平角是指过空间两条相交方向线所作的铅垂面间所夹的二面角，角值为0°~360°，水平角也可是理解为过空间两条相交方向线在水平面内的投影之间的夹角。

如图4—1所示，空间两直线OA和OB相交于点O，将点O、A、B沿铅垂方向投影到水平面上，得相应的投影点O1、A1、B1，水平线O1A1和O1B1的夹角β就是过两方向线所作的铅垂面间的夹角，即水平角。

在图4—1中，空间二面角β的测量方法是在与两个铅垂面的交线OO1垂直的平面上安置一水平度盘，使得交线OO1经过度盘中心，并且度盘处于水平状态，对以交点O为中心的水平方向线的方向值能方便地进行度量，通过望远镜瞄准远处的目标A和B，进而给出OA和OB方向线，在水平度盘上的读数分别为a和b，水平角β为两个方向读数之差：β（4—1）=ab-图4—1 水平角测量原理二、竖直角测量原理竖直角是指在同一铅垂面内，某目标方向的视线与水平线间的夹角α，也称高度角，竖直角的角值为-90°~+90°，竖直角也可以理解为某目标方向与其在水平面内投影的夹角。

视线与铅垂线的夹角称为天顶距，天顶距z 的角值范围为0~180°。

图4—2中，Z 为A 方向视线的天顶距读数。

图4—2 竖直角测量原理当视线在水平线以上时竖直角称为仰角，角值规定为正值；视线在水平线以下时为俯角，角值规定为负值。

为了测得竖直角，在经纬仪上还须安置一个竖直度盘，要使得该度盘位于铅垂面内，且该度盘中心要投影到测点上。

竖直角的大小为视线在竖盘上的读数与水平线读数之差。

通常情况下，当视线水平时，竖直度盘上的读数为90°或270°。