高二数学循环结构(201911整理)

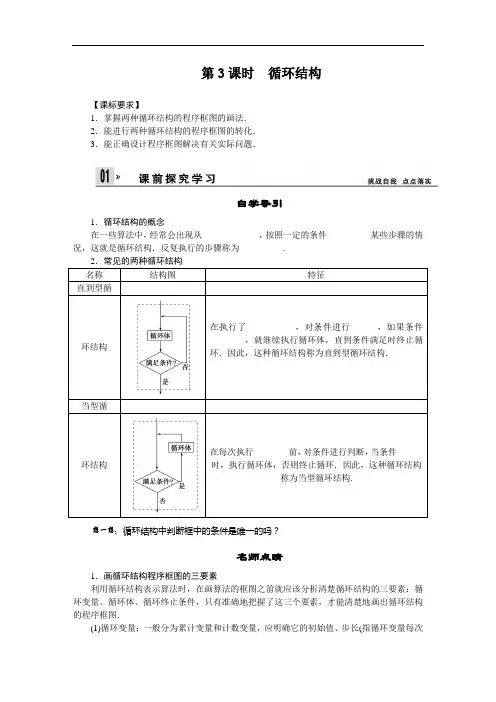
第3课时循环结构【课标要求】1．掌握两种循环结构的程序框图的画法．2．能进行两种循环结构的程序框图的转化．3．能正确设计程序框图解决有关实际问题．自学导引1．循环结构的概念在一些算法中，经常会出现从_____________，按照一定的条件__________某些步骤的情况，这就是循环结构．反复执行的步骤称为__________.：循环结构中判断框中的条件是唯一的吗？名师点睛1．画循环结构程序框图的三要素利用循环结构表示算法时，在画算法的框图之前就应该分析清楚循环结构的三要素：循环变量、循环体、循环终止条件，只有准确地把握了这三个要素，才能清楚地画出循环结构的程序框图．(1)循环变量：一般分为累计变量和计数变量，应明确它的初始值、步长(指循环变量每次增加的量)、终值．(2)循环体：也称循环表达式，它是算法中反复执行的部分．(3)循环的中止条件：程序框图中用一个判断框来表示，用它判断是否继续执行循环体．2．当型循环结构与直到型循环结构的联系和区别(1)联系①当型循环结构与直到型循环结构可以相互转化；②循环结构中必然包含条件结构，以保证在适当的时候终止循环；③循环结构只有一个入口和一个出口；④循环结构内不存在死循环，即不存在无终止的循环．(2)区别直到型循环结构是先执行一次循环体，然后再判断是否继续执行循环体，当型循环结构是先判断是否执行循环体；直到型循环结构是在条件不满足时执行循环体，当型循环结构是在条件满足时执行循环体．要掌握这两种循环结构，必须抓住它们的区别．3．计数变量与累计变量的有关理解一般地，循环结构中都有一个计数变量和累加变量：计数变量用于记录循环次数，同时它的取值还用于判断循环是否终止；累加变量用于表示每一步的计算结果．计数变量和累加变量一般是同步执行的，累加一次，计数一次．①变量i是一个计数变量，它可以统计执行的循环次数，它控制着循环的开始和结束；算法在执行循环结构时，就赋予计数变量初始值，预示循环的开始，每执行一次循环结构，计数变量的值就发生变化，并在每一次重复执行完循环体时或重新开始执行循环体时，要判断循环体的条件是否已达到终止循环的要求．②变量S是一个累加变量，它是我们编写算法中至关重要的量，我们根据要求制定它的变化情况，通常情况下与计数变量有相应关系．每执行一次循环结构，累加变量的值就发生一次变化，并在每一次重复执行完循环体时或重新开始执行循环体时，观察累加变量值的情况，并根据题意对累加变量的要求设置循环结构、终止循环的条件．题型一用循环结构解决累加、累乘问题【例1】画出求1×2×3×4×…×2 009×2 010的算法的程序框图．规律方法如果算法问题里涉及的运算进行多次重复的操作，且先后参与运算的各数之间有相同的变化规律，就可以引入循环变量参与运算，构成循环结构．在循环结构中，要根据条件设置合理的计数变量，累加(乘)变量，同时条件的表述要恰当，精确．累加变量的初值一般为0，而累乘变量的初值一般为1.【变式1】画出求3×9×27×81×…×323的算法的程序框图题型二利用循环结构寻找特定的数【例2】写出求1＋2＋3＋…＋n＞20 000的最小正整数n的算法，并画出相应的算法框图．[思路探索] 解答本题可利用累加求和的循环结构解决。

高二数学算法循环语句知识点归纳高二数学算法循环语句知识点高二数学知识点一、不等式的性质1.两个实数a与b之间的大小关系2.不等式的性质(4) (乘法单调性)3.绝对值不等式的性质(2)如果a0，那么(3)|ab|=|a||b|.(5)|a|-|b||ab||a|+|b|.(6)|a1+a2++an||a1|+|a2|++|an|.二、不等式的证明1.不等式证明的依据(2)不等式的性质(略)(3)重要不等式：①|a|0;a20;(a-b)20(a、bR)②a2+b22ab(a、bR，当且仅当a=b时取=号)2.不等式的证明方法(1)比较法：要证明ab(a0(a-b0)，这种证明不等式的方法叫做比较法.用比较法证明不等式的步骤是：作差变形判断符号.(2)综合法：从已知条件出发，依据不等式的性质和已证明过的不等式，推导出所要证明的不等式成立，这种证明不等式的方法叫做综合法.(3)分析法：从欲证的不等式出发，逐步分析使这不等式成立的充分条件，直到所需条件已判断为正确时，从而断定原不等式成立，这种证明不等式的方法叫做分析法.证明不等式除以上三种基本方法外，还有反证法、数学归纳法等.三、解不等式1.解不等式问题的分类(1)解一元一次不等式.(2)解一元二次不等式.(3)可以化为一元一次或一元二次不等式的不等式.①解一元高次不等式;②解分式不等式;③解无理不等式;④解指数不等式;⑤解对数不等式;⑥解带绝对值的不等式;⑦解不等式组.2.解不等式时应特别注意下列几点：(1)正确应用不等式的基本性质.(2)正确应用幂函数、指数函数和对数函数的增、减性.(3)注意代数式中未知数的取值范围.3.不等式的同解性(5)|f(x)|0)(6)|f(x)|g(x)①与f(x)g(x)或f(x)-g(x)(其中g(x)0)同解;②与g(x)0同解.(9)当a1时，af(x)ag(x)与f(x)g(x)同解，当0ag(x)与f(x)平方关系：sin +cos =11+tan =sec +cot =csc积的关系：sin=tancos cos=cotsin tan=sinsec cot=coscsc sec=tancsc csc=seccot 倒数关系：tan cot=1sin csc=1cos sec=1商的关系：sin/cos=tan=sec/csccos/sin=cot=csc/sec高二数学学习方法抓好基础是关键数学习题无非就是数学概念和数学思想的组合应用，弄清数学基本概念、基本定理、基本方法是判断题目类型、知识范围的前提，是正确把握解题方法的依据。

《高二数学知识点总结_高二数学算法循环语句知识点归纳》摘要：(5)|||b||b|||+|b|，(6)|(x)|g(x)①与(x)g(x)或(x)g(x)(其g(x)0);②与g(x)0，(9)当(x)g(x)与(x)g(x)当0g(x)与(x)高数学必修3课循环语句主要用实现算法循环结构若想了相关知识下面编给高二学生带数学算法循环语句知识希望对你有助高二数学算法循环语句知识高二数学知识、不等式性质两实数与b关系不等式性质() (乘法单调性)3绝对值不等式性质()如0那么(3)|b||||b|(5)|||b||b|||+|b|(6)|+++|||+||++||二、不等式证明不等式证明依据()不等式性质(略)(3)重要不等式①||0;0;(b)0(、bR)②+bb(、bR当且仅当b取)不等式证明方法()比较法要证明b(0(b0)这种证明不等式方法叫做比较法用比较法证明不等式步骤是作差变形判断()综合法从已知条件出发依据不等式性质和已证明不等式推导出所要证明不等式成立这种证明不等式方法叫做综合法(3)分析法从欲证不等式出发逐步分析使这不等式成立充分条件直到所条件已判断正确从而断定原不等式成立这种证明不等式方法叫做分析法证明不等式除以上三种基方法外还有反证法、数学归纳法等三、不等式不等式问题分类()元次不等式()元二次不等式(3)可以化元次或元二次不等式不等式①元高次不等式;②分式不等式;③无理不等式;④指数不等式;⑤对数不等式;⑥带绝对值不等式;⑦不等式组不等式应特别下列几()正确应用不等式基性质()正确应用幂函数、指数函数和对数函数增、减性(3)代数式知数取值围3不等式性(5)|(x)|0)(6)|(x)|g(x)①与(x)g(x)或(x)g(x)(其g(x)0);②与g(x)0(9)当(x)g(x)与(x)g(x)当0g(x)与(x)平方关系^+^+^^+^^积关系倒数关系商关系高二数学学习方法抓基础是关键数学习题无非就是数学概念和数学思想组合应用弄清数学基概念、基定理、基方法是判断题目类型、知识围前提是正确把握题方法依据只有概念清楚方法全面遇到题目就能很快得到题方法或者面对新习题就能想到我们平做习题方法达到迅速答弄清基定理是正确、快速答习题前提条件特别是立体几何等节复习对基定理熟悉和灵活掌握能使习题答条理清楚、逻辑推理严密反会使题速慢逻辑混乱、叙述不清严防题海战术做习题是了巩固知识、提高应变能力、思维能力、计算能力学数学要做定量习题但学数学并不等做题各种考试题有相当习题是靠简单知识堆积利用公理化知识体系演绎而就能这些习题是要通做定量习题达到对题方法展移而实现但随着高考改革高考已把考重放创造型、能力型考上因要精做习题知识理和灵活应用当你做完道习题不访问题考了什么知识?什么方法?我们从得到了题什么方法?这类习题有什么题通性?实现问题完全我应用了怎样题策略?只有这样才会培养己悟性与创造性开发其创造力也将遇到即将临期末考试和高考题目那些综合性强题目可以有科学方法它归纳数学思维数学学习其主要目是了培养我们创造性培养我们处理事情、问题能力因对处理数学问题策略、思维掌握显得特别重要平学习应重归纳它平听课明知学生应该听老师对该题目分析和归纳但还有不少学生不教师分析往往沉静老师讲每步计算、每步推证程听课是认真但费力听完是满脑子计算程支离破碎老师分析是引导学生思考启发学生己设计出处理这些问题策略、思维当教师答习题学生要用己计算和推理已知道老师要干什么另外当题目答案给出并不代表问题答完毕还要花定认真总结、归纳理记忆要把这些题策略全部纳入己脑海成永久地记忆变己这类型问题验和技能也了学生会听课而不会做题目坏毛病积累考试验学期每月初都有考试加每单元单元测验和模拟考试有十几次抓住这些机会积累定考试验掌握定考试技巧使己应有水平考试得到充分发挥其实考试是单兵作战它是考验人承受能力、接受能力、问题等综合能力战场这些能力只有平考试得到培养和训练猜你感兴趣高二数学统计知识总结高二数学知识总结全3高二上数学知识总结高二数学排列与组合知识总结5高二数学二项式定理知识梳理6高二数学函数知识总结。