《电工学》秦曾煌第六版上下册课后答案.......

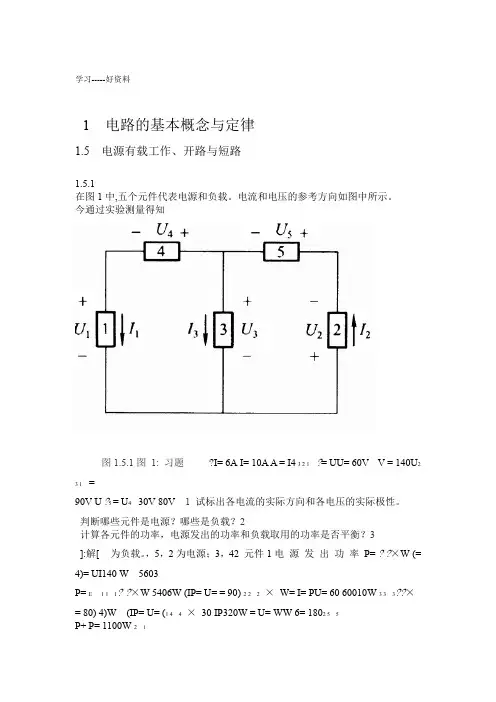
学习-----好资料1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。

电流和电压的参考方向如图中所示。

今通过实验测量得知图1.5.1图1: 习题?I= 6A I= 10A A = I43 2 1 ?= UU= 60V V = 140U23 1 =90V U?5 = U4 30V 80V 1 试标出各电流的实际方向和各电压的实际极性。

判断哪些元件是电源？哪些是负载？2计算各元件的功率，电源发出的功率和负载取用的功率是否平衡？3]:解[为负载。

，5，2为电源；3，42 元件1电源发出功率P= ??×W (=4)= UI140 W 5603P= E 1 1 1??×W 5406W (IP= U= = 90) 2 2 2×W= I= PU= 60 60010W 3 3 3??×= 80) 4)W (IP= U= (1 4 4×30 IP320W = U= WW 6= 1802 5 5P+ P= 1100W 2 1负载取用功率P = P+ P+ P= 1100W 5 4 3两者平衡1.5.2在图2中，已知I和其两端I中的电流试确定电路元件mA= ImA= 3,1.33 12更多精品文档．学习-----好资料电压U，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

3更多精品文档．学习-----好资料[解] 首先根据基尔霍夫电流定律列出图2: 习题1.5.2图?? = 0 + III 2 1 3?? = 0 I1 3 + 3可求得I的实际方向与图中的参考方向相反。

?I2mA, = 33根据基尔霍夫电流定律可得?3 3 ×××)10V = 60V = U(30 + 10 103 3其次确定电源还是负载：从电压和电流的实际方向判定：1电路元件3 电流I从“+”端流出,故为电源; 3电流I从“+”端流出，故为电源；80V元件2电流I从“+”端流出，故为负载。

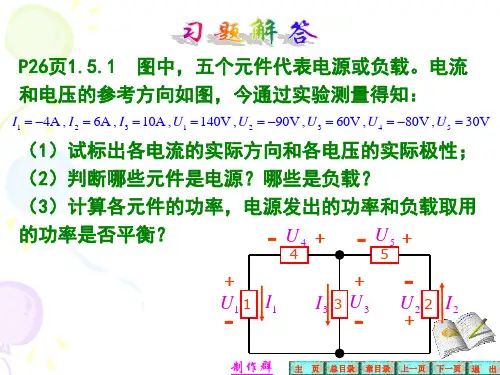
1 电路的基本概念与定律电源有载工作、开路与短路电源发出功率P E =在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

[解] 首先根据基尔霍夫电流定律列出图 2: 习题图−I1 + I2 −I3=−3 + 1 −I3=可求得I3= −2mA, I3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V= 60V其次确定电源还是负载：1 从电压和电流的实际方向判定：电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出，故为电源；电流I1从“+”端流出，故为负载。

2 从电压和电流的参考方向判别：电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(−2) ×10−3W =−120 ×10−3W （负值），故为电源；80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×10−3W =80 ×10−3W （正值），故为电源；30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×10−3 W =90 ×10−3W （正值），故为负载。

两者结果一致。

最后校验功率平衡：电阻消耗功率:2 2P R= R1I= 10 ×3 mW = 90mW12 2P R= R2I= 20 ×1 mW = 20mW2电源发出功率:P E = U2I2 + U3I3 = (80 + 120)mW =200mW负载取用和电阻损耗功率:P = U1I1 + R1 I2 + R2I2 = (90 + 90 + 20)mW =200mW1 2两者平衡基尔霍夫定律试求图6所示部分电路中电流I、I1和电阻R，设U ab = 0。

第14章晶体管起放大作用的外部条件，发射结必须正向偏置，集电结反向偏置。

晶体管放大作用的实质是利用晶体管工作在放大区的电流分配关系实现能量转换。

2．晶体管的电流分配关系晶体管工作在放大区时，其各极电流关系如下：C B I I β≈(1)E B C B I I I I β=+=+C C BB I I I I ββ∆==∆3．晶体管的特性曲线和三个工作区域 （1）晶体管的输入特性曲线：晶体管的输入特性曲线反映了当UCE 等于某个电压时，B I 和BEU 之间的关系。

晶体管的输入特性也存在一个死区电压。

当发射结处于的正向偏压大于死区电压时，晶体管才会出现B I ，且B I 随BE U 线性变化。

（2）晶体管的输出特性曲线：晶体管的输出特性曲线反映当B I 为某个值时，C I 随CE U 变化的关系曲线。

在不同的B I 下，输出特性曲线是一组曲线。

B I =0以下区域为截止区，当CE U 比较小的区域为饱和区。

输出特性曲线近于水平部分为放大区。

（3）晶体管的三个区域：晶体管的发射结正偏，集电结反偏，晶体管工作在放大区。

此时，C I =b I β，C I 与b I 成线性正比关系，对应于曲线簇平行等距的部分。

晶体管发射结正偏压小于开启电压，或者反偏压，集电结反偏压，晶体管处于截止工作状态，对应输出特性曲线的截止区。

此时，B I =0，C I =CEO I 。

晶体管发射结和集电结都处于正向偏置，即CE U 很小时，晶体管工作在饱和区。

此时，C I 虽然很大，但C I ≠b I β。

即晶体管处于失控状态，集电极电流C I 不受输入基极电流B I 的控制。

14．3 典型例题例14．1 二极管电路如例14．1图所示，试判断二极管是导通还是截止，并确定各电路的输出电压值。

设二极管导通电压D U =。

25610VD1(a)(b)(c)(d)例图解：○1图（a ）电路中的二极管所加正偏压为2V ，大于D U =，二极管处于导通状态，则输出电压0U =A U —D U =2V —=。

图3-1t rad f /3145014.322=⨯⨯==πωA t i V t u )90314sin(2)45314sin(310︒-=︒+=︒=︒--︒=-=135)90(45i u ψψϕs T x 0075.0501360135360135=⨯︒︒=︒︒=25A t i i t A t t i f ）（，时，）（︒+=∴︒=∴===+=+⨯===3040sin 10305sin 10040sin 10)40sin(225402πψψψπψπππω︒∠=∠︒∠=︒∠=︒∠⨯︒∠=⋅+=+-+=-+=+++=+1.877.145657.51.53101.9857.5645657.51.531042)44()86(1210)44()86(21212121A A A A j j j A A j j j A A 2121)2(;)60sin(10,)sin(5)1(i i i A t i A t i +=︒+==ωω︒∠=︒∠+︒∠=+=︒∠=︒∠=∙∙∙∙∙89.4023.13601005)2(;6010,05)1(2121m m m m m I I I A I A I A I A I V U 25,10,22021===第3-1 已知正弦电压和正弦电流的波形如图3-1所示,频率为50Hz ，试指出它们的最大值、初相位以及它们之间的相位差，并说明哪个正弦量超前，超前多少度？超前多少时间？ 解：u 、i 的表达式为即：u 比i 超前135°，超前2-1 某正弦电流的频率为20Hz ，有效值为 A ，在t =0时，电流的瞬时值为5A ，且此时刻电流在增加，求该电流的瞬时值表达式。

解：3-3 已知复数A 1=6+j8Ω，A 2=4+j4Ω，试求它们的和、差、积、商。

解：3-4 试将下列各时间函数用对应的相量来表示。

解：3-5 在图3-2所示的相量图中，已知 ，它们的角频率是ω，试写出各正弦量的瞬时值表达式及其相量。

目录第21章触发器和时序逻辑电路4第21.1节双稳态触发器 (4)第21.1.7题 (4)第21.1.8题 (4)第21.1.9题 (5)第21.1.10题 (5)第21.1.11题 (7)第21.2节寄存器 (8)第21.2.1题 (8)第21.3节计数器 (8)第21.3.1题 (8)第21.3.4题 (11)第21.3.5题 (11)第21.3.6题 (12)第21.3.8题 (12)第21.3.9题 (13)第21.6节应用举例 (13)第21.6.1题 (13)第21.6.3题 (15)第21.6.4题 (16)第21.6.5题 (16)1状态表 (5)2移位(右移)状态表 (9)34位二进制减法计算器的状态表 (10)4状态表 (12)5状态表 (13)6状态表 (14)7六拍通电环形分配器的状态表 (15)8状态表 (17)1习题21.1.7图 (4)2习题21.1.8图 (4)3习题21.1.9图 (5)4习题21.1.9图 (6)5习题21.1.10图 (6)6习题21.1.10图 (6)7习题21.1.11图 (7)8习题21.1.11图 (7)9习题21.1.11图 (8)10习题21.2.1图 (8)11习题21.3.1图 (9)12习题21.3.4图 (11)13习题21.3.5图 (11)14习题21.3.6图 (12)15习题21.3.8图 (13)16习题21.3.9图 (14)17习题21.6.1图 (15)18习题21.6.3图 (16)19习题21.6.4图 (16)20习题21.6.4图 (17)21习题21.6.5图 (18)21触发器和时序逻辑电路21.1双稳态触发器21.1.7根据图1(a)的逻辑图及图1(b)所示相应的CP，R D和D的波形，试画出Q1端和Q2端的输出波形，设初始状态Q1=Q2=0。

[解]Q1和Q2的波形如图1(b)所示。

图1:习题21.1.7图21.1.8电路如图2(a)所示，试画出Q1和Q2的波形。

第14章晶体管起放大作用的外部条件，发射结必须正向偏置，集电结反向偏置。

晶体管放大作用的实质是利用晶体管工作在放大区的电流分配关系实现能量转换。

2．晶体管的电流分配关系晶体管工作在放大区时，其各极电流关系如下：C B I I β≈(1)E B C B I I I I β=+=+C C BB I I I I ββ∆==∆3．晶体管的特性曲线和三个工作区域 （1）晶体管的输入特性曲线：晶体管的输入特性曲线反映了当UCE 等于某个电压时，B I 和BE U 之间的关系。

晶体管的输入特性也存在一个死区电压。

当发射结处于的正向偏压大于死区电压时，晶体管才会出现B I ，且B I 随BE U 线性变化。

（2）晶体管的输出特性曲线：晶体管的输出特性曲线反映当B I 为某个值时，C I 随CE U 变化的关系曲线。

在不同的B I 下，输出特性曲线是一组曲线。

B I =0以下区域为截止区，当CE U 比较小的区域为饱和区。

输出特性曲线近于水平部分为放大区。

（3）晶体管的三个区域：晶体管的发射结正偏，集电结反偏，晶体管工作在放大区。

此时，C I =b I β，C I 与b I 成线性正比关系，对应于曲线簇平行等距的部分。

晶体管发射结正偏压小于开启电压，或者反偏压，集电结反偏压，晶体管处于截止工作状态，对应输出特性曲线的截止区。

此时，B I =0，C I =CEO I 。

晶体管发射结和集电结都处于正向偏置，即CE U 很小时，晶体管工作在饱和区。

此时，C I 虽然很大，但C I ≠b I β。

即晶体管处于失控状态，集电极电流C I 不受输入基极电流B I 的控制。

14．3 典型例题例14．1 二极管电路如例14．1图所示，试判断二极管是导通还是截止，并确定各电路的输出电压值。

设二极管导通电压D U =0.7V 。

25610VD1(a)(b)(c)(d)例14.1图解：○1图（a ）电路中的二极管所加正偏压为2V ，大于DU =0.7V ，二极管处于导通状态，则输出电压0U =A U —D U =2V —0.7V=1.3V 。

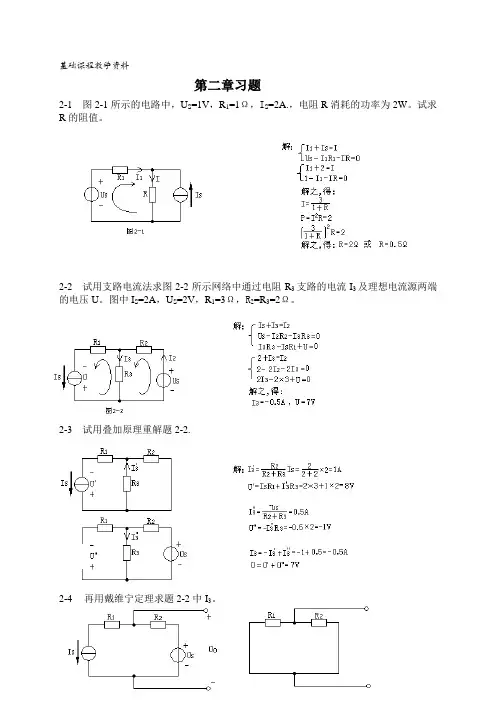
基础课程教学资料第二章习题2-1 图2-1所示的电路中，U S=1V，R1=1Ω，I S=2A.，电阻R消耗的功率为2W。

试求R的阻值。

2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。

图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。

2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。

2-5 图2-3所示电路中,已知U S1=6V，R1=2Ω，I S=5A，U S2=5V，R2=1Ω，求电流I。

2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。

求开关S在位置1和位置2两种情况下，电流I分别为多少？2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。

2-8 电路如图2-6所示，试用叠加原理求电流I。

2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。

2-10电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。

2-11 画出图2-9所示电路的戴维宁等效电路。

2-12 图2-10所示的电路接线性负载时，U 的最大值和I的最大值分别是多少？2-13 电路如图2-11所示，假定电压表的内阻无穷大，电流表的内阻为零。

当开关S处于位置1时，电压表的读数为10V，当S处于位置2时，电流表的读数为5mA。

试问当S处于位置3SHI 4，电压表和电流表的读数各为多少？2-14 图2-12所示电路中，各电源的大小和方向均未知，只知每个电阻均为6Ω，又知当R=6Ω时，电流I=5A。

今欲使R支路电流I=3A，则R应该多大？2-15 图2-13所示电路中，N为线性有源二端网络，测得AB之间电压为9V，见图（a）；若连接如图（b）所示，可测得电流I=1A。

现连接如图（c）所示形式，问电流I为多少？2-16 电路如图2-14所示，已知R1=5Ω时获得的功率最大，试问电阻R是多大？本章小结1、支路电流法是分析和计算电路的基本方法，适用于任何电路。

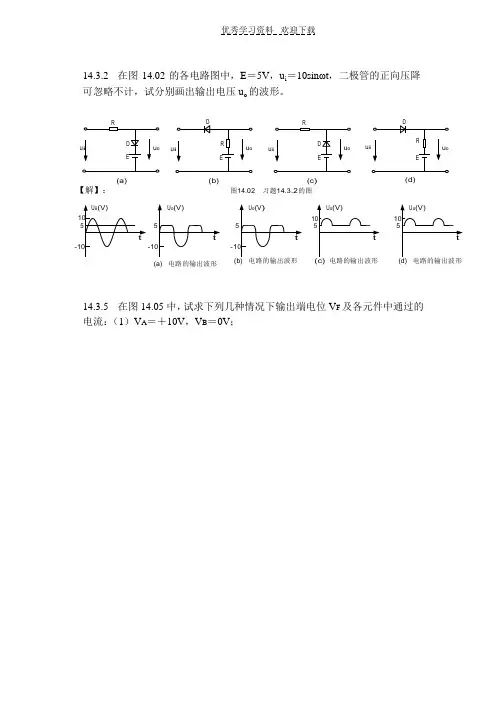
优秀学习资料欢迎下载14.3.2 在图14.02 的各电路图中，E＝5V，u i＝10si nωt，二极管的正向压降可忽略不计，试分别画出输出电压u o 的波形。

u u(a)(b)(c)(d)【解】：图14.02 习题14.3.2的图(a) 电路的输出波形14.3.5 在图14.05 中，试求下列几种情况下输出端电位V F 及各元件中通过的电流：（1）V A＝＋10V，V B＝0V；优秀学习资料欢迎下载3（2）V A＝＋6V，V B＝＋5.8V；（3）V A＝V B＝＋5V，设二极管的正向电阻为零，反向电阻无穷大。

【解】：（1）D A 优先导通9V AVF=1+ 9×10VV= 9V9V B FIDA= IR= F =R9 ×103A = 1mA图14.05 习题14.3.5的图D B 截止，I DB＝0（2）设D A 和D B 两管都导通，应用节点电压法计算V F6+5.81 1，V F = 1 1++1 11V = 5.59V < 5.8V9可见D B 管的确都导通。

IDA=6 −5.591×103A = 0.41mA，IDB= 5.8 −5.91×103A = 0.21mA，IR= 5.599×10A = 0.62mA（3）D A 和D B 两管都能导通5+5V = 1 1 V= 4.47V , I=VF =4.47A = 0.53mAF 1 1 1++1 1 9R R 9 ×10 3IDA= IDB=IR2=0.53mA = 0.26mA214.4.2 有两个稳压管D Z1 和D Z2，其稳定电压分别为5.5V 和8.5V，正向压降都是0.5V。

如果要得到0.5V、3V、6V、9V 和14V 几种稳定电压，这两个稳压管（还有限流电阻）应该如何联结？画出各个电路。

【解】：＋＋5V＋6V－－－＋＋9V6V－14.3.2在图1所示的各电路图中，E = 5V ，u i = 10 sin ωtV ，二极管D的正向压降可忽略不计，试分别画出输出电压u0 的波形。

图1: 习题1.5.1图I1 = −4A U1 = 140V U4 = −80V I2 = 6AU2 = −90V U5 =30VI3 = 10AU3 = 60V1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。

电流和电压的参考方向如图中所示。

今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。

2 判断哪些元件是电源？哪些是负载？3 计算各元件的功率，电源发出的功率和负载取用的功率是否平衡？[解]:2 元件1，2为电源；3，4，5为负载。

3 P1 = U1I1 = 140 ×(−4)W = −560W P2 = U2I2 = (−90) ×6W =−540W P3 = U3I3 = 60 ×10W =600WP4 = U4I1 = (−80) ×(−4)W =320W P5 = U5I2 = 30 ×6W =180WP1 + P2 =1100W负载取用功率P = P3 + P4 + P5 =1100W两者平衡电源发出功率P E = 1.5.21。

1欢迎下载在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

22欢迎下载。

[解] 首先根据基尔霍夫电流定律列出图 2: 习题1.5.2图−I1 + I2 −I3=−3 + 1 −I3=可求得I3= −2mA, I3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V= 60V其次确定电源还是负载：1 从电压和电流的实际方向判定：电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出，故为电源；电流I1从“+”端流出，故为负载。

第一章习题1－1 指出图1－1所示电路中A 、B 、C 三点的电位。

图1－1 题 1－1 的电路解：图（a ）中，电流 mAI 51226.=+=, 各点电位 V C = 0V B = 2×1.5 = 3V V A = (2+2)×1.5 = 6V图（b ）中，电流mAI 1246=+=， 各点电位 V B = 0V A = 4×1 = 4VV C =－ 2×1 = －2V图（c ）中，因S 断开，电流I = 0， 各点电位 V A = 6V V B = 6VV C = 0 图（d ）中，电流mAI 24212=+=， 各点电位 V A = 2×(4+2) =12VV B = 2×2 = 4V V C = 0图（e ）的电路按一般电路画法如图，电流mAI 12466=++=，各点电位 V A = E 1 = 6VV B = (－1×4)+6 = 2V V C = －6V1－2 图1－2所示电路元件P 产生功率为10W ，则电流I 应为多少? 解：由图1－2可知电压U 和电流I 参考方向不一致，P = －10W ＝UI 因为U ＝10V , 所以电流I ＝－1A图 1－2 题 1－2 的电路1－3 额定值为1W 、10Ω的电阻器，使用时通过电流的限额是多少？ 解：根据功率P = I 2 R A R P I 3160101.===1－4 在图1－3所示三个电路中，已知电珠EL 的额定值都是6V 、50mA ，试问哪个电珠能正常发光？图 1－3 题 1－4 的电路解：图（a ）电路，恒压源输出的12V 电压加在电珠EL 两端，其值超过电珠额定值，不能正常发光。

图（b ）电路电珠的电阻Ω=Ω==120120506K R .，其值与120Ω电阻相同，因此电珠EL 的电压为6V ，可以正常工作。

图（c ）电路，电珠与120Ω电阻并联后，电阻为60Ω，再与120Ω电阻串联，电珠两端的电压为V4126012060＝＋⨯小于额定值，电珠不能正常发光。

14.3.8在图14.29所示电路，试求：下列几种情况下输出端Y的电位VY及各元件（R，DA，DB）中通过的电流：（1）VA=VB=0V；（2）VA=+3V，VB=0V；（3）VA=VB=+3V。

二极管的正向压降可忽略不计。

VA=VB=0时，即DA，DB均导通，由欧姆定律IR= E/R=12/3.9=3.08mAIA，IB是两个二极管中电流，于是IA=IB=0.5IR=1.54mA，VY=0VA=3V，VB=0时，VB较低，DB先导通，使VY=0， DA截止，IA=0，于是IR =IB =12/3.9=3.08mA，IA=0VA=VB =+3V，两个二极管同时导通，使VY=+3V，IR=（12-3)/3.9=2.30mAIA=IB=0.5IR=0.5（12-3）/3.9=1.15mA14.3.9在图14.30所示电路中，试求下列几种情况下输出端电位VY及各元件中通过的电流：（1）VA=+10V，VB=0V;（2）VA=+6V，VB=+5.8V；（3）VA=VB=+5V。

设二极管的正向电阻为零，反向电阻无穷大。

VA=+10V，VB=0时，DA导通，VA导通 VY=10*9/（1+9）=9VDB截止，于是由欧姆定律IA=VA/（1+9）=10/10=1mAIB =IA = 1mA，IB=0（2） VA=6V，VB=5.8V时，DA先导通，使VY=6*9/（1+9）=5.4V，DB=端电压VBY=VB-VY=5.8-5.4=0.4V设二极管正向电阻为0，于是DB导通，由支路电流法IA+9(IA+IB)=VAIB+9(IA+IB)=VB所以(IA+IB)(1+9+9)=VA+VB由KCL定律IR=IA+IB所以IR=(VA+VB)/19=(6+5.8)/19=0.62mA所以，由欧姆定律VY=IR*R=0.62*9=5.59V于是IA=(6-5.59)/1=0.41mAIB=(5.8-5.59)/1=0.21mA（3）VA=VB=5V，两个二极管同时导通。

14二极管和晶体管14.3二极管14.3.2在图1所示的各电路图中，E = 5V , U i = 10 sin ®tV ,二极管D的正向压降可忽略不计，试分别画出输出电压U o的波形。

［解］(町(b)图1:习题14.3.2图(a)U i为正半周时，U i > E，D导通；U i < E，D截止。

U i为负半周时，D截止。

D导通时，U o = E； D截止时，U o = U i。

(b)U i为正半周时；U i > E, D导通；U i < E, D截止。

U i为负半周时，D截止。

D导通时，U o = U i ； D截止时，U o = E。

U0的波形分别如图2(a)和(b)所示。

图2:习题14.3.2图14.3.5在图3中，试求下列几种情况下输出端电位V Y 及各元件中通过的电流。

(1)V A = +10V ，V B = 0V ； (2)V A = +6V ,V B = +5.8V ;(3)V A = V B = +5V .设二极管的正 向 电阻为零，反向电阻为无穷大。

［解］图3:习题14.3.5图(1) 二极管D A 优先导通，则D B 反向偏置，截止，I D B = 0⑵ 设D A 和D B 两管都导通，应用结点电压法计算V Y :11.8 X 9V = 5.59V < 5.8V19 可见D B 管也确能导通I D A= A = 0.41 X 10?3A = 0.41mADA1 X 1035.8 ?5.59八 cc, ,c?3I D B = T A = 0.21 X 10 A = 0.21mA B1 X 103叫 1 kQ y™ 斤t —J —1—V Y I D A10 9 X K = 9VI R =V Y~R 9 9 X 103X10?3 A = 1mAV Y = 1 1 1 1 + +5.59 ?3I R = 3A = 0.62 X 10'3A = 0.62mA9 X 103⑶ D A 和D B 两管都能导通5 5 + —V Y = [ 1 [ 1 [ V = 4.74V+ + - 1 1 9 I R = _ V Y - ■ - 4.74 八 A =0.53 X10?3A = 0.53mAI RD A I D BmA = 0.26mA2 214.4 稳压二极管 14.4.2有两个稳压二极管 是0.5V 。