网格中的三角函数

1网格中的锐角三角函数网格是同学们从小就熟悉的图形，在网格中隐含的条件有：1.直角；2.单位长度。

所以在网格中可以求一个锐角的三角函数，是近几年中考的热点，下面举例说明。

一、在网格中与勾股定理现结合求一个锐角的三角函数。

【例1】 三角形在正方形网格纸中的位如图1，则sin α的值是( ).[解析] 本题在网格中考查锐角的正弦的意义，首先要用勾股定理计算直角三角形斜边的长．一般情况下，为了减小计算量，把小正方形的边长设为1．选C ．练习1（广州市2014）如图2，在边长为1的小正方形组成的网格中，的三个顶点均在格点上，则（ ）．（A ） （B ） （C ） （D ）练习2 （2014年福州）如图3，在边长为1个单位长度的小正方形所组成的网格中，△ABC 的顶点均在格点上，344543B .； C .35；D .A. 35图3图22sinB 的值是 .3.（2011四川）如图4，在4×4的正方形网格中， tanα= .A ．1B ．2C ．12D4.（2011甘肃兰州）如图5，A 、B 、C 三点在正方形网格线的交点处，若将△ACB 绕着点A 逆时针旋转得到△AC’B’，则tanB’的值为 .A ．12B ．13C ．14 D3. （2011江苏连云港）如图6，△ABC 的顶点都在方格纸的格点上，则sin A =_______.在网格中求一个锐角的三角函数时，根据图中角的位置。

充分利用网格中的直角和边，然后根据勾股定理求出相应的边长，最后利用三角函数公式进行计算，达到解决问题的目的。

二、在网格中与辅助线相结合求一个锐角的三角函数。

【例2】 （2014•贺州）如图7-1网格中的每个小正方形的边长都是1，△ABC 每个顶点都在网格的交点处，则sinA= ．[解析] 虽然网格中隐含直角，但是∠A 是△ABC中图7-1图7-2图4图6图5的一个锐角，而△ABC不是直角三角形，不能直接运用三角函数公式进行计算，必须先做辅助线构造直角三角形，使∠A在一个直角三角形中，然后求出所对应的斜边和对边，而后解决问题。

锐角三角函数值的求解攻略浙江嘉善县泗洲中学（314100）杨晓霞［摘要］锐角三角函数是历年中考数学的重点和热点内容，研究锐角三角函数对中考应用题的复习备考乃至中考数学命题模式的把握都有非常重要的指导意义.［关键词］三角函数；锐角；求解［中图分类号］G633.6［文献标识码］A［文章编号］1674-6058（2021）08-0020-02一、定义法［例1］如图1，在Rt△ABC中，∠ACB=90°，BC=3，AC=15，AB的垂直平分线DE交BC的延长线于点D，垂足为E，求sin∠CAD的值.分析：在图1中，∠CAD为直角三角形CAD的一个内角，根据锐角的正弦的定义，可知sin∠CAD=CDAD.因此，本题的解题关键是求出∠CAD的对边CD和斜边AD的长度.根据线段的垂直平分线的性质易知AD=BD.已知条件BC=3，可表示出CD长.在Rt△CAD中运用勾股定理求解.当然，这里最好引入一个未知数，以简便表示相关线段长度.解：因为AB的垂直平分线DE交BC的延长线于点D，所以有AD=BD.不妨设AD=BD=x，又BC=3，则CD=x-3，而AC=15，在Rt△CAD中，根据勾股定理知AC2+CD2=AD2，即15+()x-32=x2，解得x=4.即AD=4，CD=1，所以sin∠CAD=CDAD=14.点评：本题主要考查锐角三角函数中正弦的定义，并检测学生对一元二次方程的求解的掌握程度，勾股定理在解题中起了关键作用.二、参数法［例2］如图2，在△ABC中，∠C=90°，sin A=25，求sin B的值.分析：根据已知条件中的sin A=25，可以结合锐角三角函数中正弦的定义，引入一个参数，设出角A的对边CB和斜边AB的长度，再运用勾股定理求得角A的邻边AC的长度后，问题得解.解：因为∠C=90°，sin A=25，根据此比值可设CB=2x，AB=5x，其中x>0，再由勾股定理得AC2=AB2-CB2=21x2，即AC=21x，结合锐角三角函数中正弦的定义可知，sin B=ACAB=21x5x=点评：熟练掌握锐角三角函数中正弦的定义是解决本题的关键所在，若已知条件中给出具体角的比值，通常的做法是引入一个大于0的参数，根据比值设出相应边的长度，然后根据勾股定理求解.三、构造法1.三角形中的构造［例3］如图3，在直角△BAD中，延长斜边BD到点C，使得DC=12BD，连接AC，若tan B=53，求tan∠CAD的值.分析：本题要求tan∠CAD，但由于∠CAD不在图中已知的直角三角形中，需要另外构造直角三角形，使得∠CAD置于其中.可以过点D作边AD的垂线，构造出直角三角形ADH来解决.解：过点D作边AD的垂线DH交AC于H，垂足为D，如图4所示，根据△BAD为直角三角形可知，∠BAD=∠ADH=90°，所以AB∥DH，易证得△CDH∽△CBA，进而得到DH AB=CD CB，因为已知条件中有DC=12BD，则DH AB=CD CB=13，又在Rt△BAD中，tan B=53，不妨设AD=5k，AB=3k，这样DH=k，故在Rt△ADH中，有tan∠CAD=DHAD=k5k=15.点评：如果在三角形中求相关角的三角函数值时，所求角并不在已知直角三角形中，这时我们就需要通过作垂线段来构造直角三角形，从而将所求角置于直角三角形中，再结合三角函数值的定义求解.本题还运用了相似三角形的相关性质.此外，本题亦可图1图2图3图4［基金项目］本文系全国教育科学“十三五”规划2017年度教育部重点课题“核心素养视角下的中学数学命题模式研究”（批准号：DHA17035）成果.数学·解题研究过点C 作直线AD 的垂线，通过构造出两个相似的直角三角形，利用相似比计算出相应的边长求解.2.圆中的构造［例4］如图5，在半径为3的圆O 中，直径AB 与弦CD 相交于点E ，连接AC ，BD ，若AC =2，求tan D 的值.分析：题中已知条件提及直径AB ，又要求角D 的正切值，自然联想到这里应该是要借助“直径AB 所对的圆周角为直角”这一性质来构造直角三角形，然后将角D 置于其中求解.解：连接BC ，如图6所示，因为AB 为直径，则∠ACB =90°，这样在直角三角形ACB 中，有tan A =BCAC，根据圆周角的性质，不难发现∠A =∠D ，故tan D =BCAC，又圆O 的半径为3，AC =2，那么BC =AB 2-AC 2=36-4=42，所以tan D =BCAC=422=22.点评：在圆中求锐角三角函数值时，利用直径来构造直角三角形是最常用的构造方法，一般还会利用“同弧（或等弧）所对的圆周角相等”这一性质，将目标角进行等量转化.3.网格中的构造［例5］如图7所示，已知△ABC 的三个顶点均在格点上，则cos A 的值为.图7图8分析：因为网格中无直角三角形，所以需要借助网格格点构造直角三角形，不妨通过点B 来构造，连接格点B 、D ，如图8所示，易知△ABD 为直角三角形.解：如图8所示，连接格点B 、D ，根据正方形的对角线的特征，易知△ABD 为直角三角形，可设小正方形的边长为1，则AB =10，AD =22，所以cos A =AD AB =2210=255.点评：在网格中求锐角三角函数值，一般都是借助网格中的格点去构造直角三角形，通常构造的方法也不是唯一的，本题也可以通过补网格，利用格点C 来构造直角三角形.四、等量转化法1.网格中的转化［例6］如图9，在边长相同的小正方形网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB 、CD 相交于点P，则tan∠APD 的值为.图9图10分析：本题可将∠APD 转化为∠BPC ，然后通过小正方形的对角线构造直角三角形解决.解析：连接格点B 、Q ，交DC 于点H ，如图10所示，则BH ⊥DC ，所以tan∠APD =tan∠BPH =BHPH ，若设小正方形的边长为1，那么BH=易知△BDP ∽△ACP ，则DP PC =BD AC =13，所以DP =14DC=那么PH =DH -DP 故tan∠APD =BH PH =22=2.点评：在网格中，若对所求角直接构造直角三角形较困难，可以进行适当的等量转化.本题将∠APD 等量转化为∠BPC 是解题的关键.2.折叠中的转化［例7］如图11，在△ABC 中，∠ACB =90°，AC =BC =4，将△ABC 折叠，使点A 落在BC边上的点D 处，EF 为折痕，若AE =3，则sin∠BFD =.分析：根据折叠的性质，∠A =∠EDF =45°，注意到∠BFD =180°-∠B -∠BDF =135°-∠BDF ，∠CDE =180°-∠EDF -∠BDF =135°-∠BDF .这样将∠BFD 等量转化成∠CDE ，再在Rt△CDE 中求解.解析：由题意知，∠A =∠EDF =∠B =45°，在△BFD 中，∠BFD =180°-∠B -∠BDF =135°-∠BDF ，又因为∠CDE =180°-∠EDF -∠BDF =135°-∠BDF ，所以∠BFD =∠CDE ，易知CE =1，DE =3，故sin∠BFD =sin∠CDE =CE DE =13.点评：折叠问题中，要紧扣相关角、边之间的等量关系.将∠BFD 等量转化成∠CDE 是成功解决本题的关键一步.锐角三角函数值的求解是中考数学的必考题型，其涉及的题目类型多变，可采用的解题策略也较多，在平时的教学过程中，教师要注意归纳、小结各种解题方法，以便学生在解题时可以信手拈来.（责任编辑黄桂坚）图5图6图11数学·解题研究。

选填分类汇编-网格中的三角函数
1.如图，点,,A B O 是正方形网格上的三个格点，O 的半径为OA ，点P 是优弧AmB 上的一点，则tan APB ∠的值是( )
A.1
B.2
C.3 2.如图，将AOB ∠放置在55⨯的正方形网格中，则cos AOB ∠的值是( )
A.23
B.32 3.如图，ABC 的顶点都在方格纸的格点上，则sin A =__________．
4.如图所示，网格中的每个小正方形的边长都是1，ABC 每个顶点都在网格的交点处，则sin A =__________．
5.如图，ABC 的顶点都在正方形网格的格点上，则cos C =__________．
答案
1.A
2.C
3.答案：5
解析：过点C 作CD AB ⊥交AB 的延长线于点D ．
设小正方形的边长为1，
在Rt ACD 中，2CD =，AC =，
sin
5CD A AC ∴=
==． 4.答案：35
解析：由已知可得111162422246222
ABC S =-⨯⨯-⨯⨯-⨯⨯=． 过点C 作AB 的垂线交AB 于点H .
勾股定理可得AB AC ==
162
ABC S AB CH ∴=⋅=．
解得CH =
3sin 5A ∴∠=
．
5.解析：过A 作AD 垂直CB 的延长线于点D
在格点三角形ADC 中，2AD =，4CD =，
所以AC =
=，
所以cos
CD C AC
===。

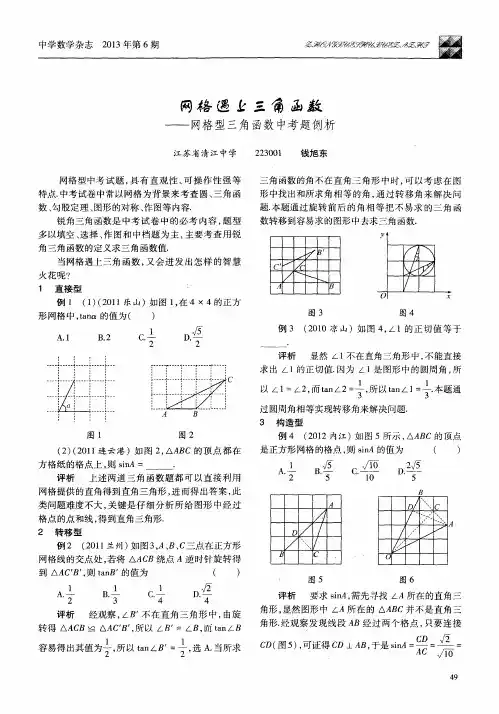
网格线中的三角函数问题作者：周宏伟来源：《初中生世界·九年级》2016年第12期在我们常见的网格线中，有很多三角函数求值问题，题中蕴含着很多思想方法，为便于大家复习，现归纳如下，供大家在学习过程中参考.一、补形的策略例1 （2015·山西）如图1，在网格中，小正方形的边长均为1，点A、B、C都在格点上，则∠ABC的正切值是（）.A.2B.[255]C.[55]D.[12]【方法探究】如何把∠ABC放在某个直角三角形中是解决本题的关键，仔细观察可以发现：AB在小正方形的对角线上，能联想到45°角，只要连接AC即可构造出直角，然后在直角三角形中运用三角函数的定义求解.【过程展示】如图2，连接AC，则∠CAB=90°，在Rt△ABC中，tan∠ABC=[ACAB]=[12].故选D.例2 （2016·福建福州）如图3，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点.已知菱形的一个角（∠O）为60°，A、B、C都在格点上，则tan∠ABC的值是 .【方法探究】观察网格的特点，首先考虑如何将∠ABC放到一个直角三角形中，这是解决问题的关键.【过程展示】如图4，连接DA，DC，则点B、C、D在同一直线上，设菱形的边长为a，由题意得∠ADF=30°，∠BDF=60°，∴∠ADB=90°，AD=[3a]，DB=2a，tan∠ABC=[ADBD]=[3a2a]=[32]，故答案为[32].二、转化的思想例3 （2012·江苏泰州）如图5，在由边长相同的小正方形组成的网格中，点A、B、C、D 都在这些小正方形的顶点上，AB、CD相交于点P，则tan∠APD的值为 .【方法探究】直接求∠APD的正切值比较困难，可以考虑利用线段的平移对∠APD进行转化，找出它的“替身”，然后进行求解，以达到化难为易的目的.【过程展示】如图6，取小正方形的顶点E，连接AE、BE，由图可知CD∥BE，∴∠APD=∠ABE，在Rt△ABE中，tan∠ABE=2，∴tan∠APD=2.例4 （2016·山东淄博）图7是由边长相同的小正方形组成的网格，A、B、P、Q四点均在正方形网格的格点上，线段AB、PQ相交于点M，则图中∠QMB的正切值是（）.A.[12]B.1C.[3]D.2【方法探究】如果直接求tan∠QMB可考虑连接AP、BQ，运用△APM∽△BQM求出AM或BM，然后在Rt△APM或Rt△BQM中求解；如果间接求解，应考虑对∠QMB进行转化，最好的思路是考虑线段的平移.①如图8，平移AB至A′Q，在Rt△A′PQ中求tan∠Q；②如图9，平移AB至PB′，在Rt△B′PQ中求tan∠P；③如图10，平移PQ使其经过线段AB中点D，然后在Rt△ACD中求tan∠ADC.【过程展示】以第①种平移为例，如图8，平移AB至A′Q后，∠Q=∠QMB，在Rt△A′PQ中，tan∠Q=[A′PA′Q]=2，所以tan∠QMB=2.故选D.三、等积法例5 （2015·四川乐山）如图11，已知△ABC的三个顶点均在格点上，则cosA的值为（）.A.[33]B.[55]C.[233]D.[255]【方法探究】通过作三角形的高构造直角三角形，先利用等积法（或勾股定理）求出高，然后运用余弦的定义解答.【过程展示】如图11，设小正方形的边长为1，过点B作AC边上的高BD.由勾股定理得：AC=[32]，AB=[10]，由等积法可得：[12]BC∙h=[12]∙AC∙BD，即[12]×2×3=[12]×[32]∙BD，解得BD=[2]，由勾股定理，得AD=[AB2-BD2]=[22]，∴cosA=[ADAB]=[2210]=[255].故选D.例6 （2014·广西贺州）如图12，网格中的每个小正方形的边长都是1，△ABC每个顶点都在网格的交点处，则sinA= .【方法探究】在替换与∠A相等的角比较困难的情况下，可以考虑通过作高进行构造，把∠A放在某个直角三角形中进行求解.【过程展示】如图12，过点C作CE⊥AB，垂足为E，连接AD，则AD⊥BC，从不同的角度把△ABC的面积计算两次得：S△ABC=[12]AB∙CE=[12]BC∙AD，所以[12]×[25]×CE=[12]×[22]×[32]，所以CE=[655]，在Rt△ACE中，sin∠CAE=[CEAC]=[65525]=[35].由此可见，遇到网格中的锐角三角函数求值问题，我们通常有两种思路：一是原地不动，想办法构造直角三角形求解；二是转移该角，如利用平行线进行转化.一般情况下，遇到求三角函数问题优先考虑转化，在没有好的转化思路的情况下再考虑如何构造.（作者单位：江苏省东台市新街镇中学）。

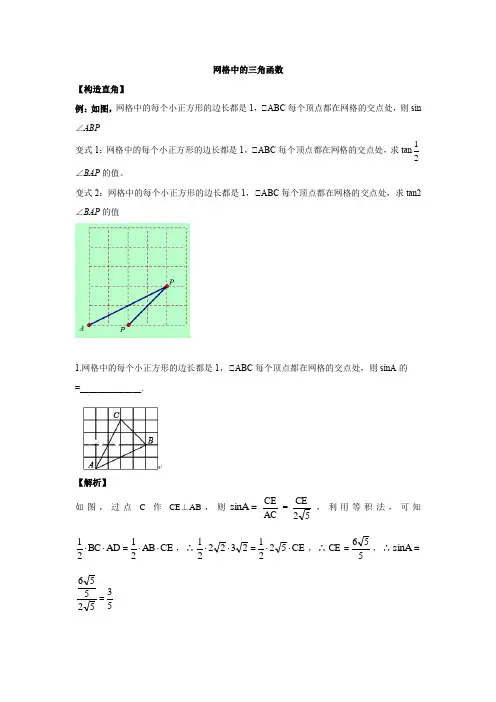
网格中的三角函数【构造直角】例：如图，网格中的每个小正方形的边长都是1，△ABC 每个顶点都在网格的交点处，则sin ∠ABP变式1：网格中的每个小正方形的边长都是1，△ABC 每个顶点都在网格的交点处，求tan 12∠BAP 的值。

变式2：网格中的每个小正方形的边长都是1，△ABC 每个顶点都在网格的交点处，求tan2∠BAP 的值1.网格中的每个小正方形的边长都是1，△ABC 每个顶点都在网格的交点处，则sinA 的=______________.【解析】如图，过点C 作CE ⊥AB ，则=A sin AC CE =52CE ，利用等积法，可知CE AB 21AD BC 21⋅⋅=⋅⋅，∴CE 5221232221⋅⋅=⋅⋅，∴556CE =，∴=A sin 5352556=【等角转换】 2.如图，在边长相同的小正方形组成的网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB 、CD 相交于点P ，则tan ∠APD 的值是 ．【解析】思路一：构造直角连接BE ，由四边形EDBC 为正方形可知，CD ⊥BE ，∴tan△APD=tan△BPF=PFBF，设小正方形边长为2（可自己思考一下为什么？），可得BF=1，CD=2，由△APC ∽△BPD ，且相似比为3：1可得3DP PC =，∴43CD PC =，∴PC=432⋅=23，∴PF=PC —CF=21，∴tan△BPF=2211=思路二：角度转换连接BE ，可知BE ∥CD ，∴△APD=△BPF=△ABE ，连接AE ，∵AE 和BE 均为正方形对角线，易得AE ⊥BE ，∴tan△ABE=2BEAE=3.如图，在边长相同的小正方形网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB ，CD 相交于点P ， 则PBAP的值= ，tan ∠APD 的值= ．4.如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC 的顶点都在格点上，则图中△ABC 的余弦值是_________.5.如图，在网格中，小正方形的边长均为1，点A ，B ，C 都在格点上，则△ABC 的正切值是________.6.如图，在正方形网格中，△ABC 的顶点都在格点上，则tan ∠ACB 的值为 ．7.如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点．已知菱形的一个角（∠O ）为60°，A ，B ，C 都在格点上，则tan ∠ABC 的值是 ．8.如图，网格中的四个格点组成菱形ABCD ，则tan ∠DBC 的值为_________．9.如图1是由边长为1的小正方形组成的网格，点A 、B 、C 、D 都在网格的格点上，AC 、BD 相交于点O ．10.（一）探索发现（1）如图1，当AB=2时，连接AD ，则∠ADO=90°，BO=2DO ，AD=2，BO=232，tan ∠AOD=_________．如图2，当AB=3时，画AH ⊥BD 交BD 的延长线于H ，则AH=223， BO=________，tan ∠AOD=________． 如图3，当AB=4时，tan ∠AOD=__________．（2）猜想：当AB=n （n ＞0）时，tan ∠AOD=______________．（结果用含n 的代数式表示），请证明你的猜想． （二）解决问题（3）如图，两个正方形的一边CD 、CG 在同一直线上，连接CF 、DE 相交于点O ，若tan ∠COE=1317，求正方形ABCD 和正方形CEFG 的边长之比．【解析】（一）探索发现（1）如图1，当AB=2时，∵BO=2DO ，BO=232， ∴OD=32，又∵∠ADO=90°，AD=2，∴tan ∠AOD=322ODAD==3，即tan ∠AOD=3． 如图2，设DCBE 为正方形，连接CE ，交BD 于F ． ∵四边形BCDE 是正方形， ∴DF=CF=BF=21BD=21CE ，BD ⊥CE ． 根据题意得：AB ∥DC ，∴△AOB ∽△COD ，∴DO ：BO=CD ：AB ．当AB=3时，DO ：BO=1：3，∴BO=423． ∵S △ABD =21BD •AH=21AB •ED ，∴BD •AH=AB •ED ， ∴AH=22323BD ED AB ==⋅， DO ：BO=CD ：AB=1：3，∴DO ：DF=1：2，∴OF ：DF=1：2，即OF ：CF=1：2． 在Rt △OCF 中，tan ∠COF=OFCF=2， ∵∠AOD=∠COF ，∴tan ∠AOD=2；如图3，当AB=4时，DO ：BO=CD ：AB=1：4， ∴DO ：DF=1：2.5=2：5，∴OF ：DF=3：5，即OF ：CF=3：5． 在Rt △OCF 中，tan ∠COF=35OF CF =， ∵∠AOD=∠COF ，∴tan ∠AOD=35；故答案是：3；423；2；35；（2）猜想：当AB=n （n ＞0）时，tan ∠AOD=1-n 1n +（结果用含n 的代数式表示）． 证明：过点A 作AH ⊥BH 于点H ，则AH=BH=22n ． ∵AB ∥OD ，∴△AOB ∽△COD ，∴1nCD AB OD OB ==， ∴OB=1n n 2+．∴OH=BH ﹣OB=22n ﹣1n n 2+．∴tan ∠AOD=1-n 1n +； 故答案是：1-n 1n +；（二）解决问题（3）解：如图4，过点D 作DH ⊥CF 于点H ，则tan ∠DOH=HODH． ∵∠DOH=∠COE ， ∴tan ∠DOH=1317， 又由（一）结论得：13171-n 1n =+， ∴n=215 ∴正方形ABCD 和正方形CEFG 的边长之比为215． 强化训练11.阅读下面的材料：某数学学习小组遇到这样一个问题： 如果α，β都为锐角，且tan α=，tan β=，求α+β的度数．该数学课外小组最后是这样解决问题的：如图1，把α，β放在正方形网格中，使得∠ABD=α，∠CBE=β，且BA ，BC 在直线BD 的两侧，连接AC ． （1）观察图象可知：α+β= °；（2）请参考该数学小组的方法解决问题：如果α，β都为锐角，当tan α=3，tan β=时，在图2的正方形网格中，画出∠MON=α﹣β，并求∠MON 的度数．12.问题呈现如图1，在边长为1的正方形网格中，连接格点D ，N 和E ，C ，DN 和EC 相交于点P ，求tan ∠CPN 的值． 方法归纳求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形．观察发现问题中∠CPN不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题，比如连接格点M，N，可得MN∥EC，则∠DNM=∠CPN，连接DM，那么∠CPN就变换到Rt△DMN中．问题解决（1）直接写出图1中tan∠CPN的值为；（2）如图2，在边长为1的正方形网格中，AN与CM相交于点P，求cos∠CPN 的值；思维拓展（3）如图3，AB⊥BC，AB=4BC，点M在AB上，且AM=BC，延长CB到N，使BN=2BC，连接AN交CM的延长线于点P，用上述方法构造网格求∠CPN 的度数．13．（1）在△ABC中，AB、BC、AC三边的长分别为、、，求这个三角形的面积．如图1，某同学在解答这道题时，先建立一个每个小正方形的边长都是1的网格，再在网格中画出边长符合要求的格点三角形ABC（即△ABC三个顶点都在小正方形的顶点处），这样不需要求△ABC的高，而借用网格就能就算出它的面积．请你将△ABC的面积直接填写在横线上．思维拓展：（2）已知△ABC三边的长分别为a（a＞0），求这个三角形的面积．我们把上述求△ABC面积的方法叫做构图法．如图2，网格中每个小正方形的边长都是a，请在网格中画出相应的△ABC，并求出它的面积．类比创新：（3）若△ABC三边的长分别为（m＞0，n ＞0，且m≠n），求出这个三角形的面积．如图3，网格中每个小长方形长、宽都是m，n，请在网格中画出相应的△ABC，用网格计算这个三角形的面积．14．如图，在每个小正方形的边长为1的网格中，点A，B，C均在格点上．（1）AB的长等于；（2）在△ABC的内部有一点P，满足S△PAB ：S△PBC：S△PCA=1：2：3，请在如图所示的网格中，用无刻度的直尺，画出点P，并简要说明点P的位置是如何找到的（不要求证明）．15．如图，在由完全相同的小正方形组成的网格中，△ABC的三个顶点都在格点上．（1）请在网格中找一个格点P，连接PB、PC，使∠BPC=∠BAC，并简要说明理由；（2）直接写出此时tan∠BPC的值．16．如图，在正方形网格中，每个小正方形的边长都为1，点A点B在网格中的位置如图所示．（1）建立适当的平面直角坐标系，使点A点B的坐标分别为（1，2）（4，3）；（2）点C的坐标为（3，6），在平面直角坐标系中找到点C的位置，连接AB、BC、CA，则∠ACB=°；（3）将点A、B、C的横坐标都乘以﹣1，纵坐标不变，分别得到点A1、B1、C1，在图中找到点A1、B1、C1并顺次连接点A1、B1、C1，得到△A1B1C1，则这两个三角形关于对称．17．如图，在正方形网格中建立平面直角坐标系，格点O为原点，格点A的坐标为（﹣1，3）．（1）画出点A关于y轴对称的格点B，并写出点B的坐标（，）；（2）将线段OA绕着原点O顺时针旋转90°，点A落在格点C处，画出线段OA扫过的平面区域（用阴影表示），则AC的长为；（3）过点C作AC的切线CD，D为格点，设直线CD的解析式为y=kx+b，y 随x的增大而；（填“增大”或“减小”）（4）连接BC，则tan∠BCD的值等于．。

初中网格中的数学问题赏析在正方形的网格中，每个小正方形的边长都是相等的，每个小正方形的顶点叫做格点，我们把以格点的连线为边的图形叫格点图形.近年来，各地的中考试卷中频频出现这类与格点有关的数学问题，由于这类与网格有关的中考题大部分具有开放性，设计又新颖，能很好地考查学生的思维水平和思维能力，故很受命题者的青睐.但课本、作业本中这类问题的例题和习题却并不多见，在此，特作梳理，与大家一起赏析.一、网格中的三角形1. （2010·湖南）如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（）.A． 6 B． 7 C． 8 D． 9分析根据题意，结合图形，分两种情况讨论（如下图）：① AB为等腰△ABC 底边，符合条件的C点有4个；② AB为等腰△ABC其中的一条腰，符合条件的C点有4个.故选C.本题考查了等腰三角形的判定，解答本题关键是根据题意，画出符合实际条件的图形，再利用数学知识来求解.数形结合的思想是数学解题中很重要的解题思想.本题是利用网格提供的相等线段来构图.2. 在如图的方格纸中，每个小方格都是边长为1的正方形，点A、B是方格纸中的两个格点（即正方形的顶点），在这个5×5的方格纸中，找出格点C使△ABC 的面积为2个平方单位，则满足条件的格点C的个数是（）.A. 5B. 4C. 3D. 2分析 A、B两点的垂直距离为2，那么，只要保证水平距离为2即可使△ABC的面积为2个平方单位；A、B两点的水平距离为1，那么，只要保证垂直距离为4，即可使△ABC的面积为2个平方单位.符合条件的点坐标分别为：C（3，1），C（0，3），C（4，3），C（1，5）.本题考查三角形面积的求法，注意分水平距离和垂直距离两种情况，数学分类思想是一种重要的数学思想.二、网格与三角函数1. （2010·贵州）在正方形网格中，△ABC的位置如图所示，则cos∠B的值为 .分析过点C向上作垂线与AB相交于点D，则∠B是Rt△BCD的一个内角，邻边和斜边均由图可知，所以很容易求出cos∠B的值.或是过点A作垂线交BC的延长线于D，也可求出.本题主要考查了余弦函数的定义，正确理解定义是解题的关键.本题是利用网格提供的垂线，构建直角三角形.2. （2010·四川）如图，∠D的正切值等于 .分析根据同弧所对的圆周角相等，可以把求三角函数的问题，转化为直角三角形边的比的问题.先利用同弧所对圆周角相等，得出∠D=∠A，然后利用正切等于对边比上邻边即可求出.本题考查圆周角的性质及锐角三角函数的概念：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边.从网格中很容易找到相关的直角三角形.三、网格与面积1. （2006·苏州）如图，直角坐标系中，△ABC的顶点都在网格点上，其中A点坐标为（2，－1），则△ABC的面积为平方单位.分析根据图形，可以直接写出点A的坐标是（2，-1）.分别过A、B、C三点作垂线，形成一个大矩形，求出大矩形的面积，用大矩形的面积减去三个直角三角形的面积，剩余的面积即为△ABC的面积.此类题要求学生要能够把不规则图形的面积转化为规则图形的面积.有关面积的割补法是解决不规则图形面积的常用方法.本题充分利用网格的特点，构建规则图形.2. （2009·吉林）如图，小正方形边长为1，连接小正方形的三个顶点，可得△ABC，则AC边上的高是 .分析先用大正方形的面积减去三个直角三角形的面积得到△ABC的面积，△ABC的面积又等于AC乘以AC边上的高的一半，按这一等量关系列出方程，解出方程即可得出AC边上的高.四、网格与相似如图，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在方格纸的格点上.（1）?摇判断△ABC和△DEF是否相似，并说明理由；（2）?摇P，P，P，P，P，D，F是△DEF边上的7个格点，请在这7个格点中选取3个点作为三角形的顶点，使构成的三角形与△ABC相似（要求写出2个符合条件的三角形，并在图中连结相应线段，不必说明理由）.分析答案为：△DPP、△DPP、△DPP.本题主要考查学生识图、构图能力和对三角形相似判定知识的理解，对学生的观察力有一定的挑战性.网格中的相等线段以及相等的角对构图起到关键性的作用.五、网格与圆1. （2010· 河北）如图，在5×5正方形网格中，一条圆弧经过A、B、C三点，那么这条圆弧所在圆的圆心是 .分析连接BC，弦AB、BC垂直平分线的交点即为圆心.本题主要考察学生对垂径定理的理解，和残圆确定圆心的方法.本题是由网格特点直接看出线段的垂直平分线.2. （2010·江苏）．如图，在4×4的方格纸中（共有16个小方格），每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点，则扇形OAB的弧长等于（结果保留根号及π）.分析连接AB、AC，分别作它们的垂直平分线，两线交点即为圆心.利用勾股定理求出圆的半径，由图可知扇形OAB圆心角为90°，利用弧长公式即可求出弧长.本题考查了勾股定理及弧长公式的应用.解题的关键是正确地求出扇形的圆心角及半径.3. 如图所示，△ABC的三个顶点的坐标分别为A（-1,3）、B（-2,-2）、C（4,-2），则△ABC外接圆半径的长度为 .分析先求出线段AB、 AC、 BC的长度，再利用余弦定理求角A的余弦值，从而得到角A的正弦值.再利用正弦定理，即可求得直径.半径为2.连接OC因为C（4，-2），利用勾股定理得半径的长等于根号下，等于，化简为2.六、网格中的运动（2010·江苏）如图在网格图中，⊙A的半径为2个单位长度，⊙B的半径为1个单位长度，要使运动的⊙B与静止的⊙A相内切，应将⊙B由图示位置向左平移个单位长度.分析⊙B与⊙A可以在右边相内切，也可以在左边相内切.当⊙B与⊙A在右边相内切，移动距离为4个单位长度，当⊙B与⊙A在左边相内切，移动距离为6个单位长度.故答案为：4或6.本题主要通过圆的移动来考查圆与圆的位置关系；题目中小圆向左移动，通过观察，可知两圆内切的两种情况，分别求出移动的距离.七、网格与图形的变换1. （2010·辽宁）如图，在边长为1的小正方形组成的网格中，△ABC的顶点均在格点上，请按要求完成下列各题：（1）以直线BC为对称轴作△ABC的轴对称图形，得到△ABC，再将△ABC绕着点B逆时针旋转90°得到△ABC，请依此画出△ABC、△ABC；（2）求线段BC旋转到BC过程中所扫过的面积（计算结果用π表示）；（3）求点C旋转过程所经过的路径长.分析（1）根据对称的性质，画出图形；（2）BC旋转到BC的过程中，旋转角为90°，半径为4，由弧长公式计算即可.所以B点所经过的路线长度是2π.本题考查了学生画一个图形的对称图形以及弧长公式的应用的能力.2. （2010·湖北）如图，在方格纸上△DEF是由△ABC绕定点P顺时针旋转得到的.如果用（2，1）表示方格纸上A点的位置，（1，2）表示B点的位置，那么点P的位置为（）.A. （5，2）B. （2，5）C. （2，1）D. （1，2）分析连接AD、CF，再做这两线段的垂直平分线，交点就是点P.根据点A、点B 的坐标建立平面直角坐标系，然后写出点P的坐标.此题属于中等难度题，主要考查的知识点是旋转及其相关的性质，旋转的中心在连接对应点的垂直平分线上，做出两条垂直平分线，它们的交点就是旋转的中心点.3. （2010· 甘肃）如图均为7×6的正方形网格，点A、B、C在格点（小正方形的顶点）上.（1）在图中确定格点D，并画出一个以A、B、C、D为顶点的四边形，使其为轴对称图形；（2）在图中确定格点E，并画出一个以A、B、C、E为顶点的四边形，使其为中心对称图形.分析第（1）题可以将点A向下平移四格得到点D，或是将点A向右平移两格得到点D.第（2）题可以将点A向右平移一格得到点E，两题方法均不唯一，此题比较灵活地考查了等腰梯形、平行四边形、矩形的对称性，是道好题.八、网格与概率一只蚂蚁在如图所示的图案内任意爬动一段时间后停下，蚂蚁停在阴影内的概率为 .分析先确定黑色区域的面积与总面积的比值，此比值即为所求的概率.本题主要考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率.网格对化不规则图形为规则图形提供了帮助，方便学生求出阴影部分的面积.九、网格与规律（2006·温州）在边长为l的正方形网格中，按下列方式得到“L”形图形，第1个“L”形图形的周长是8，第2个“L”形图形的周长是，第三个“L”形图形的周长是，则第n个“L”形图形的周长是 .分析第1个“L”形图形的周长是8＝4＋4，第2个“L”形图形的周长是12＝4＋2×4，第3个“L”形图形的周长是16＝4＋3×4，……，第n个“L”形图形的周长是4＋n×4，即4n＋4．本题也可以这样来分析：平移“L”形的上面和右下的两边，第1个“L”形图形周长变成一个正方形周长加上4，即4＋4，第2个“L”形图形周长为4＋2×4，第3个“L”形图形周长为4＋3×4，第n个“L”形图形的周长是4＋n×4.用整式描述几何图形的规律在近几年的中考题中经常出现，这类题目把几何和整式结合起来考查，使试题难度增大.它既考查学生的识图能力，又考查学生的判断推理能力.通过以上分析，我们不难发现：网格中的数学问题，往往是把网格的特点与数学问题有机结合起来.网格可以提供相等的线段、相等的角、垂线、平行线、化不规则图形为规则图形等.还能够很方便地进行图形的翻折、平移、旋转等.同学们在解决这类问题时，既要有札实的数学基础，灵活运用相关数学知识，还要注意结合网格的特点来分析和解决问题.。

一、网格题型在中考数学中的10大考点梳理网格问题，近年来在一些省市的中考试卷中频频出现，这类问题虽然出现在小网格中，却隐藏着大智慧，从中可以开发智力，发展思维．笔者以中考试题为例，说明小网格中的大智慧．一、正方形网格（一）全网格形全网格形是指有完整的网格的题型．1．网格中求坐标例1：如图1，在一单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…都是斜边在x轴上、斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A t(2，0)，A2（1，－1），A3(0，0)，则依图中所示规律，A2012的坐标为________．分析：由于2012是4的倍数，故A1~A4；A5～A8；…每4个为一组，可见，A2012在x轴上方，横坐标为2，再根据纵坐标变化找到规律即求得纵坐标为1006．答案：(2，1006)2．网格与等腰三角形例2：如图2所示的正方形网格中，网格线的交点称为格点°已知A、B是两格点，如果C 也是图中的格点，且使得△ABC为等腰三角形，则点G的个数是()(A)6(B)7(C)8(D)9分析：有两种情况：①AB为等腰△ABC底边，C在A B的中垂线上，因此，符合条件的C点有4个；②AB为等腰ABC其中的一条腰，符合条件的C点有4个，应选C．本题考查了等腰三角形的判定，解答本题关键是根据题意，画出符合实际条件的图形．3．网格与直角三角形例3：如图3，在网格中有一个直角三角形（网格中的每个小正方形的边长均为1个单位长度）．若以该三角形一边为公共边画一个新三角形与原来的直角三角形一起组成一个等腰三角形，要求新三角形与原来的直角三角形除了有一条公共边外，没有其它的公共点，新三角形的顶点不一定在格点上．那么符合要求的新三角形有()(A)4个(B)6个(C)7个(D)9个分析：根据题意可知：如图4，以原三角形AB边为公共边的三角形有4个，分别如图上D1，D2，D3，D4；以原三角形BC边为公共边的三角形有2个，分别如图上D5，D6；以原三角形AC边为公共边的三角形只有1个，如图上D．符合要求新三角形有7个，选C例4：如图5是5×5的正方形网格，△ABC的顶点都在小正方形的顶点上，像△ABC这样的三角形叫格点三角形．画与△ABC有一条公共边且全等的格点三角形，这样的格点三角形最多可以画出_______个．分析：如图6，以BC为公共边可画出△BDC，△BEC，△BFC三个三角形和原三角形全等；以AB为公共边可画出三个三角形△ABC、△ABM、△AB H和原三角形全等，所以可画出6个．5．网格与相似例5：图7所示4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是()[来源学*科*网][来源学科网Z XX K]分析：根据勾股定理，得BC＝，AB，AC；根据勾股定理的逆定理可判断△ABC为直角三角形，∠ABC＝90°，BC：AB＝1：2．在四个图形中，显然答案B中的三角形为直角三角形且两条直角边的比为1：2，选B．例6：如图8，在3×5的正方形网格中，每个小正方形的边长为1，求图中点A到P Q的距离A H的长．分析：连结A P，AQ组成一个三角形．你可以用长方形面积减去三个直角三角形求得[来源学科网]出△A P Q的面积，而S△A P Q＝12P Q×A H，P Q的长用勾股定理计算，求得答案为755．7．网格中求三角函数[来源:Z xx k.C o m]例7：如图9，在正方形网格中有△ABC，则s i n∠ABC的值等于()（A）31010（B）1010（C）13（D）10分析：首先利用勾股定理分别算出AB、BC、AC的长度，再利用勾股定理的逆定理得出∠ACB＝90°，最后根据锐角三角函数的定义求出s i n∠ABC的值，选B．8．网格与圆例8：如图10，边长为1的小正方形构成的网格中，半径为1的⊙O 的圆心O 在格点上，点A 、B 、C 、E 也都在格点上，CB 与⊙O 相交于点D ，连结ED ，则∠AED 的正切值等于_______．分析：本题是锐角三角函数的定义和圆周角的运用，解答本题的关键是利用同弧所对的圆周角相等把求∠AED 的正切值转化成求∠ACB 的正切值．tan ∠AED ＝tan ∠ABC ＝12AC AB ．（二）局部网格形局部网格形指是网格图案的一部分，需要通过添线补全网格的题型．例9：如图11(1)，每个小正方形的边长为1，A 、B 、C 是小正方形的顶点，则∠ABC 的度数为()(A )90°(B )60°(C )45°(D )30°分析：先把局部网格补全成如图11(2)所示，易见△ACD 与△CBE 全等，可得出AC ＝BC ，∠ACB ＝90°，所以∠ABC ＝45°．选C ．二、长方形网格例10：如图12，在长方形网格中，每个小长方形的长为2，宽为1，A、B两点在网格格点上，若点C也在网格格点上，以A、B、C为顶点的三角形面积为2，则满足条件的点C 个数是()(A)2(B)3(C)4(D)5[来源学科网]分析：底和高分别是4和1的有两个，底和高分别是2和2的有两个，选C．二、中考网格型试题赏析近几年中考中，网格型试题可谓大放异彩，这类试题构思精巧、形式活泼，能很好地考查图形变换、勾股定理、相似等数学知识，体现分类讨论、数形结合等重要的数学思想，当网格作为背景与双曲线、抛物线、圆、三角形结合时，更会出现许多让人意想不到的思路、方法，使我们在解题中感受到无穷的乐趣，本文撷取其中的几例进行解析，供参考．一、网格与双曲线结合例1：在边长为1的4×4方格上建立直角坐标系（如图1），在第一象限内画出反比例函数16y x =、6y x =、4y x=的图象，它们分别经过方格中的一个格点、二个格点、三个格点；在边长为1的10×10方格上建立直角坐标系（如图2），在第一象限内画出反比例函数的图象，使它们经过方格中的三个或四个格点，则最多可画出()条．(A )12(B )13(C )25(D )50分析：易知系数k 为合数，且能分解成两个均不超过10的正整数的乘积的形式．如4＝1×4＝2×2，则反比例函数4y x=的图象经过以下3个格点：(1，4)，(2，2)，(4，1)．6＝1×6＝2×3，则反比例函数6y x =的图象经过以下4个格点：(1，6)，(2，3)，(3，2)，(6，1)．经过尝试，符合条件的k 值共有13个，分别为：4，6，8，9，10，12，16，18，20，24，30，36，40．所以，经过方格中的三个或四个格点的反比例函数的图象最多可以画出13条．故选B ．二、网格与抛物线结合例2：已知图3中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点，请你在图中任意画一条抛物线，问所画的抛物线最多能经过81个格点中的多少个？()(A )6(B )7(C )8(D )9分析：我们先解决如下问题：对于抛物线y ＝ax 2＋bx ＋c ，当a 、b 、c 满足什么条件时，当x 取任意整数时，函数值y 都是整数？（为叙述方便，不妨假设抛物线开口向上．）当x ＝0时，y ＝c ；当x ＝l 时，y ＝a ＋b ＋c ．∴c 为整数，a ＋b ＋c 为整数，∴a ＋b 必为整数，又∵当x ＝2时，y ＝4a ＋2b ＋c ＝2a ＋2(a ＋b )＋c 是整数，∴2a 必为整数，∴a 应为12的整数倍，即a ＝12，1，32，2，…从对称的角度考虑，建立如图4所示的平面直角坐标系．(1)若抛物线的顶点在格点上，要使抛物线尽可能多地经过格点，显然应使抛物线过原点．所画抛物线y ＝ax 2（n ＝12，1，32，2，…）最多能经过5个格点．(2)若抛物线的顶点不在格点上，要使抛物线尽可能多地经过格点，显然应使抛物线），＝ax 2＋bx ＋c 过原点和(1，0)．所画抛物线y ＝ax (x －1)（a ＝12，1，32，2，…）最多能经过8个格点．此时a ＝12，这8个格点分别为：(－3，6)，（－2，3），（－1，1），(0，0)，(1，0)，(2，1)，(3，3)，(4，6)．[来源学&科&网Z&X &X &K]综上所述，抛物线最多能经过81个格点中的8个，故选C ．三、网格与圆结合例3：请你在12×12的网格图形中任意画一个圆，则所画的圆最多能经过169个格点中的____个格点．分析：从对称的角度考虑，建立如图5所示的平面直角坐标系．(1)如图5，若圆心在格点上，要使圆尽可能多地经过格点，显然应使圆心过原点，所画圆最多能经过12个格点，此时圆的半径为5．这12个格点分别为：(0，5)，(3，4)，(4，3)，(5，0)，[来源学§科§网](4，－3)，（3，－4），（0，－5），（－3，－4），(－4，－3)，（－5，0），（－4，3），（－3，4）．(2)如图6，若圆心不在格点上，要使圆尽可能多地经过格点，显然应使圆心过（12，12），所画圆最多能经过16个格点，此时圆的半径为2，这16个格点分别为：(2，6)，(4，5)，(5，4)，(6，2)，（6，－1），（5，－3），（4，－4），（2，－5），（－1，－5），（－3，－4），（－4，－3），(－5，－1)，（－5，2），（－4，4），（－3，5），（－1，6）．综上所述，所画的圆最多能经过169个格点中的16个格点．四、网格与三角形结合例4：如图7，将△ABC 放在每个小正方形的边长为1网格中，点A 、B 、C 均落在格点上．(1)△ABC 的面积等于____；(2)若四边形DEF G 是△ABC 中所能包含的面积最大的正方形，请你在如图7所示的网格中，用直尺和三角尺画出该正方形，并简要说明画图的方法．分析：(1)S △ABC ＝12×4×3＝6；(2)如果正方形的一边落在三角形的一边上，其余两个顶点分别在三角形的另外两条边上，则这样的正方形面积是最大的．如图8，在△ABC 中，AB ＝c ，AB 边上的高CN ＝h c ，△ABC 的面积为S ，正方形的一边DE 落在AB 上，其余两个顶点F 、G 分别在BC 、AC 上．设正方形DEF G 的边长是x．所以，图8中正方形一边落在AB 边上，另两个顶点落在其他两边上时，121212744x ==+；图8中正方形一边落在BC边上，另两个顶点落在其他两边上时，图8中正方形一边落在AC 边上，另两个顶点落在其他两边上时，[来源学科网Z|X X|K]∴当正方形一边落在BC边上时，正方形DEF G的面积最大．画法一：如图9，在AB上任取一点P，作P Q⊥BC于点Q，以P Q为一边在△ABC内部画正方形P QMN；作射线BN交AC于点D，过点D作D G⊥BC于点G，作DE⊥D G交AB 于点E，过点E作EF⊥BC于点F，则四边形DEF G即为所求．证明：由画图过程易得四边形DEF G为矩形，∵D G⊥BC，NM⊥BC，∴D G//NM，画法二：如图10，取格点P，连结P C，过点A画P C的平行线，与BC交于点Q，连结P Q 与AC相交得点D；过点D画CB的平行线，与AB相交得点E，分别过点D、E画P C的平行线，与CB相交得点G、F，则四边形DEF G即为所求．证明：由画图过程易得四边形DEF G为平行四边形，[来源学科网]由格点P的位置易判断P C＝CB，且P C⊥CB，∴D G⊥CB，∴平行四边形DEF G为矩形。

格点图中的锐角三角函数正在正方形网格中，我们把水平线与竖直线相交的点称为格点。

如果在网格中，一个三角形的三个顶点在格点上，那么我们称这个三角形为格点三角形。

格点三角形有锐角三角形、直角三角形和钝角三角形三类。

在初中阶段，锐角三角函数值的求解经常作为一个考点来考查学生的观察、分析和计算能力。

由于此类题灵活多变，内容丰富，经常将其在中考试卷中作为考点进行考查，其考查学生能力的作用不言而喻。

下面择其中的中考题作个例析。

例1.如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，E为BC中点，则sin∠AEB的值是（）A．B．C．D．例1例2例2.（2017•无锡）在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A，B，C，D都在格点处，AB与CD相交于O，则tan∠BOD的值等于．练习：1.如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点．已知菱形的一个角（∠O）为120°，A，B，C都在格点上，则tan∠ABC的值是．第1题第2题2.如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点，已知菱形的一个角（如∠O）为60°，A，B，C，D都在格点上，且线段AB、CD相交于点P，则tan∠APC 的值是．3.仿照例题完成任务：例：如图1，在网格中，小正方形的边长均为1，点A，B，C，D都在格点上，AB与CD相交于点O，求tan∠BOD的值．解析：连接AE，EF，导出∠BOD＝∠FAE，再根据勾股定理求得三角形各边长，然后利用三角函数解决问题．具体解法如下：连接AE，EF，则AE∥CD，∴∠FAE＝∠BOD，根据勾股定理可得：AE＝，AF＝2，EF＝3，∵，∴△FAE是直角三角形，∠FEA＝90°，∴tan∠FAE＝＝3，即tan∠BOD＝3．任务：（1）如图2，M，N，G，H四点均在边长为1的正方形网格的格点上，线段MN，GH相交于点P，求图中∠HPN的正切值；（2）如图3，A，B，C均在边长为1的正方形网格的格点上，请你直接写出tan∠BAC的值．4.如图，在边长都为1的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点P，（1）sin∠BAC＝，PC＝．（2）求tan∠DPA的值．参考答案：例1.【考点】直角三角形斜边上的中线；勾股定理；勾股定理的逆定理；锐角三角函数的定义。