材力题解第8章

同学们自己总结的11材料力学考研重点我总结一下第四版的材料力学的重点，希望对大家能有一个导向的作用，注意这是第四版的，用第五版教材的每章都差不多，也有一定的借鉴价值。

第一章看第一章第三节简称1-3（以后都这样表示，单独列出的数字表示的章节都要看）,1-4（即第一章第四节要仔细看）,1-5。

第二章看2-1,2-2，例题2-1,2-3，公式的推导过程，就是关于积分的那部分不用看，只记住最后的公式就行了，例题2-2，例题2-3（这个题和专业课笔记上的那个很相似，是应该记住的题型），2-4，例题2-5关于变形的协调关系是重点，2-5,2-6这一节容易出选择，例题2-7,2-7，例题2-8,2-9,2-10.2-8不看。

思考题不做，以后的思考题如果没有特殊情况都不做。

习题2-21和2-22只写步骤，不查表。

其他习题第一遍复习时全做。

第三章看3-1，3-2，3-3例题3-1,3-4介绍的几何方面，物理方面，静力学方面是做材力题的三大步骤，要有这个概念，这一节开始接触应力状态，要看会那个框框上扎个箭头是什么意思，而且自己会画，以后到第七章的时候会大量用到。

看例题3-2，例题3-3不看，例题3-4看。

3-5，例题3-5，例题3-6,3-6，例题3-7记住里面的公式。

3-7记住那个切应力变化的示意图，图3-16，其他不看，例题3-18不做。

3-8不看。

思考题只看3-9，习题3-21到3-26不做。

第四章看4-1，例题4-1,4-2，例题4-2到例题4-9全看，例题4-10不看，例题4-11例题4-12看，4-3，例题4-13是10年真题的基础图形，看，例题4-14这个图形也考过，看，4-4，例题4-15到例题4-19,4-5，记住那四个弯曲最大切应力的公式就好，例题4-20和例题4-21看一下切应力流的变化，这点09真题考过，例题4-22看，4-6。

思考题看4-13,4-14,4-17,4-18。

习题4-4全做，其他那些画图的每题可以自己选择性的删除四分之一左右，只要练会了就行，习题4-9选做，4-10也选做吧，但是这个要记住结果，习题4-16，4-17，4-18，4-20，4-34，4-35，4-43，都不做，其余遇到选择工字钢号码的也不查表，对照答案得到最后数据，不查表，其他全做。

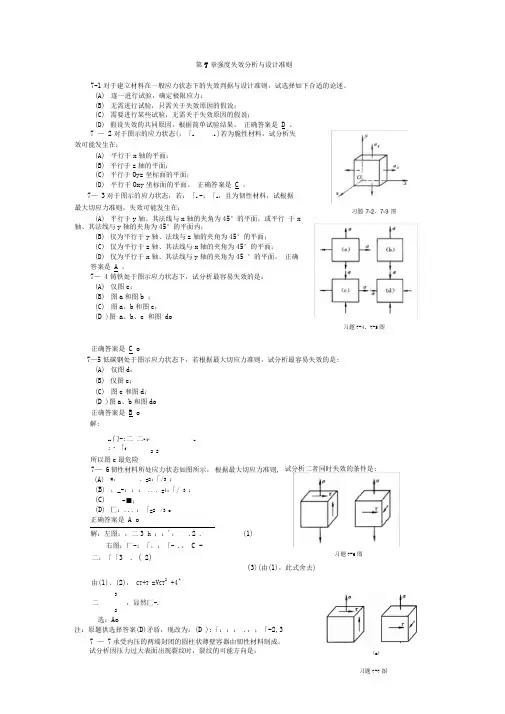
第7章强度失效分析与设计准则7-1对于建立材料在一般应力状态下的失效判据与设计准则，试选择如下合适的论述。

(A) 逐一进行试验，确定极限应力； (B) 无需进行试验，只需关于失效原因的假说； (C) 需要进行某些试验，无需关于失效原因的假说； (D) 假设失效的共同原因，根据简单试验结果。

正确答案是 D 。

7 — 2对于图示的应力状态(；「x ,y )若为脆性材料，试分析失 效可能发生在： (A) 平行于x 轴的平面； (B) 平行于z 轴的平面； (C) 平行于Oyz 坐标面的平面；(D) 平行于Oxy 坐标面的平面。

正确答案是 C 。

7— 3对于图示的应力状态，若：「y -；「x ，且为韧性材料，试根据 最大切应力准则，失效可能发生在： (A) 平行于y 轴、其法线与x 轴的夹角为45°的平面，或平行 于x 轴、其法线与y 轴的夹角为45°的平面内； (B) 仅为平行于y 轴、法线与z 轴的夹角为45°的平面； (C) 仅为平行于z 轴、其法线与x 轴的夹角为45°的平面；(D) 仅为平行于x 轴、其法线与y 轴的夹角为45 °的平面。

正确答案是 A 。

7— 4铸铁处于图示应力状态下，试分析最容易失效的是： (A) 仅图c ；(B) 图a 和图b ； (C) 图a 、b 和图c ； (D )图 a 、b 、c 和图 do习题7-4、7-5图正确答案是 C o7—5低碳钢处于图示应力状态下，若根据最大切应力准则，试分析最容易失效的是: (A) 仅图d ； (B) 仅图c ；(C) 图c 和图d ； (D )图a 、b 和图do 正确答案是 B o解:7— 6韧性材料所处应力状态如图所示， 根据最大切应力准则, (A ) W ，. =2;「/3 ；(B ) ；_-：：： .，. =4;「/ 3 ；(C ) -■；(D ) 匚：..，；「=2 /3 o正确答案是 A o解：左图：；二3 h ；：'： .2 . (1)_c门-:二 二-(Y) _:・「32 2所以图c 最危险右图：厂-；「，；「- .， C -二；「「3 . ( 2)试分析二者同时失效的条件是: 习题7-6图(3)(由(1)，此式舍去) 由(1)、(2)， CT +T =V CT 2+4^ 3二 ，显然匚-. 2选：Ao注：原题供选择答案(D )矛盾，现改为：(D );「：：： .，；「-2,3 7 — 7承受内压的两端封闭的圆柱状薄壁容器由韧性材料制成。

∴ = 0，
MPa，
MPa
MPa
2． = 248 MPa；
∴ = 0，
MPa，
MPa
MPa 3． = 290 MPa。
∴ = 0，
MPa，
MPa
MPa
7-13 铝合金制成的零件上某一点处的平面应力状态如图所示，其屈服应力 = 280MPa。试按最大切应 力准则确定。
1．屈服时的 的代数值； 2．安全因数为 1.2 时的 值。 1．解：
1．（a）
（b）
，
2．（a）
（b） 用形状改变比能，相当应力相同。
7-17 薄壁圆柱形锅炉容器的平均直径为 1250mm，最大内压强为 23 个大气压（1 个大气压 0.1MPa）， 在高温下工作时材料的屈服应力 = 182.5MPa。若规定安全因数为 1.8，试按最大切应力准则设计容器的 壁厚。
解：
，
，
习题 7-17 解图
壁厚：
mm
7-18 平均直径 D = 1.8m、壁厚 = 14mm 的圆柱形容器，承受内压作用。若已知容器为钢制，其屈服应力 = 400MPa，要求安全因数 ns = 6.0。试分别应用以下准则确定此容器所能承受的最大内压力。
1．用最大切应力准则； 2．用形状改变比能准则。
①设：
习题 7-13 图
=0
得
= 230 MPa
②设： =0
得
MPa
∴
= 230 MPa 或
MPa
2．解：
， = 168 MPa
或
，
MPa
∴
= 168 MPa 或
MPa
7-16 两种应力状态分别如图 a 和 b 所示，若二者的 、 数值分别相等，且

不相同----------应力的面的概念。
应力
指明
哪一个面上？ 哪一点？
哪一点？ 哪个方位面？
过一点不同方向面上应力的集合，
称为这一点的应力状态 State of the
Stresses of a Given Point
三、一点应力状态的描述
1. 微 元体
Element
dz
（又称应力单元体）
特点： （1）正六面体；
yx dAsin sin
y dAsin cos
yx t
y
0
整理后得到
x
y
2
x
y
2
cos 2
xy
sin
2
x
y
2
sin
2
xy
cos 2
y
有界、周期函数
x
xy
一定存在极值
求主应力的极值
d—— = 0 d
x
2
y
sin
2
xy
cos
2
0
即在=0的平面，记为0平面
x
2
y
sin
20
xy
x
n
x
yx t
y
Fn 0
dA
dA x d Acos cos xy
n
xy d Acos sin
x
α
α
x
yx dAsin cos
y dAsin sin
yx t
y
0
Ft 0
dA
n
dA x d Acos sin xy d Acos cos
xy
x
α
α
x
Principal planes

第一章绪论一、是非判断题材料力学的研究方法与理论力学的研究方法完全相同。

( × ) 内力只作用在杆件截面的形心处。

( × )杆件某截面上的内力是该截面上应力的代数和。

( × )确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ∨ )根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ∨ )根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ∨ )同一截面上正应力σ与切应力τ必相互垂直。

( ∨ )同一截面上各点的正应力σ必定大小相等，方向相同。

( × )同一截面上各点的切应力τ必相互平行。

( × )应变分为正应变ε和切应变γ。

( ∨ )应变为无量纲量。

( ∨ )若物体各部分均无变形，则物体内各点的应变均为零。

( ∨ )若物体内各点的应变均为零，则物体无位移。

( × )平衡状态弹性体的任意部分的内力都与外力保持平衡。

( ∨ )题图所示结构中，AD杆发生的变形为弯曲与压缩的组合变形。

( ∨ )题图所示结构中，AB杆将发生弯曲与压缩的组合变形。

( × )B题图题图二、填空题材料力学主要研究 受力后发生的，以及由此产生的 。

拉伸或压缩的受力特征是 ，变形特征是 。

剪切的受力特征是 ，变形特征是。

扭转的受力特征是 ，变形特征是 。

弯曲的受力特征是 ，变形特征是 。

组合受力与变形是指 。

构件的承载能力包括 ， 和 三个方面。

所谓 ，是指材料或构件抵抗破坏的能力。

所谓 ，是指构件抵抗变形的能力。

所谓 ，是指材料或构件保持其原有平衡形式的能力。

根据固体材料的性能作如下三个基本假设 ， ， 。

认为固体在其整个几何空间内无间隙地充满了组成该物体的物质，这样的假设称为 。

根据这一假设构件的 、 和 就可以用坐标的连续函数来表示。

填题图所示结构中，杆1发生 变形， 杆2发生 变形，杆3发生 变形。

材料力学性能课后习题第一章1.解释下列名词①滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

②弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

③循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

④包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

⑤塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。

⑥韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

⑦加工硬化：金属材料在再结晶温度以下塑性变形时,由于晶粒发生滑移,出现位错的缠结,使晶粒拉长、破碎和纤维化,使金属的强度和硬度升高,塑性和韧性降低的现象。

⑧解理断裂：解理断裂是在正应力达到一定的数值后沿一定的晶体学平面产生的晶体学断裂。

2.解释下列力学性能指标的意义（1）E( 弹性模量）；（2）σp（规定非比例伸长应力）、σe（弹性极限）、σs（屈服强度）、σ0.2（规定残余伸长率为0.2%的应力）；（3）σb（抗拉强度）；（4）n（加工硬化指数）;（5）δ（断后伸长率）、ψ（断面收缩率）3.金属的弹性模量取决于什么？为什么说他是一个对结构不敏感的力学性能？取决于金属原子本性和晶格类型。

因为合金化、热处理、冷塑性变形对弹性模量的影响较小。

4.常用的标准试样有5倍和10倍，其延伸率分别用δ5和δ10表示，说明为什么δ5>δ10。

答：对于韧性金属材料，它的塑性变形量大于均匀塑性变形量，所以对于它的式样的比例，尺寸越短，它的断后伸长率越大。

5.某汽车弹簧，在未装满时已变形到最大位置，卸载后可完全恢复到原来状态；另一汽车弹簧，使用一段时间后，发现弹簧弓形越来越小，即产生了塑性变形，而且塑性变形量越来越大。

试分析这两种故障的本质及改变措施。

向力 Fz = 10 kN；在齿轮 2 上，作用有切向力 F'y = 5 kN、径向力 F'z = 1.82 kN。若许用应力 [ ]=100 MPa，试根据第四强度理论确定轴径。
题 10-13 图 解：将各力向该轴轴线简化，得其受力图如图 10-13a 所示。内力图（ M z , M y 和 T ）分 别示如图 b,c 和 d。
其相当应力为 (b)
比较式(a)和(b)可知，该轴真正的危险点是截面 A-A 上水平直径的左端点，其相当应力如 式(b)所示。 顺便指出，本题计算相当应力的另一种方法是先求 ( ) 与 τ ( ) ，再求 σ r3 ( ) 。这里的
5
从截面 A-A 上左边水平半径量起，以顺钟向为正。将 σ r3 ( ) 对 求导，寻找其极值位置，找 到的极值位置是 0 ，由此确定的危险点同上述真正的危险点，相当应力当然也同式(b)。
5.19 102 m 51.9 mm
10-16
图示钢质拐轴，承受铅垂载荷 F1 与水平载荷 F2 作用。已知轴 AB 的直径为
d，轴与拐臂的长度分别为 l 与 a，许用应力为[]，试按第四强度理论建立轴 AB 的强度条件。
题 10-16 图 解：将载荷 F1 与 F2 平移到截面 B 的形心，得轴 AB 的受力如图 b 所示。 显然，固定端处的横截面 A 为危险截面，该截面的轴力、扭矩与弯矩分别为
试求偏心距 a 的许用值。
题 10-8 图 解：1.确定内力
FN 250kN，M y Fa 2.50 105 a (N m) M z 0.050F 0.050 250103 N m 1.25104 N m
2．计算 Iz，Iy 及 A
0.100 0.1203 0.080 0.0803 4 )m 1.099105 m 4 12 12 3 0.020 0.100 0.080 0.0203 4 Iy ( 2 )m 3.39 106 m 4 12 12 A (0.100 0.020 2 0.080 0.020)m2 5.60 103 m 2 Iz (

第一章绪论判断题１、根据均匀性假设，可认为构件的应力在各点处相同。

（）２、根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（）３、固体材料在各个方向具有相同力学性能的假设，称为各向同性假设。

所有工程材料都可应用这一假设。

（）４、在小变形条件下，研究构件的应力和变形时，可用构件的原始尺寸代替其变形后的尺寸。

（）5、任何物体都是变形固体，在外力作用下，都将发生变形。

当物体变形很小时，就可视其为刚体。

填空题１、材料力学的任务是。

２、为保证机械或工程结构的正常工作，其中各构件一般应满足、和三方面的要求。

3、物体受力后产生的外效应是，内效应是；材料力学研究的是效应问题。

4、认为固体在其整个几何空间毫无空隙地充满了物质，这样的假设称为假设。

根据这一假设，构件的就可用坐标的连续函数表示。

5、受外力而发生变形的构件，在外力解除够后具有消除变形的这种性质称为；而外力除去后具有保留变形的这种性质为。

选择题1、根据均匀性假设，可认为构件的（）在各点处相同。

A 应力B 应变C 材料的弹性常数D 位移2、根据各向同性假设，可认为构件的（）在各方向都相同。

A 应力B 应变C 材料的弹性常数D 位移3、确定截面的内力的截面法，适用于（）。

A 等截面直杆B 直杆承受基本变形C 直杆任意变形D 任意杆件4、构件的强度、刚度和稳定性( )。

A 只与材料的力学性质有关B 只与构件的形状尺寸有关C 与A、B都有关D 与A、B都无关5、各向同性假设认为，材料沿各个方向具有相同的( )。

A 外力B 变形C 位移D 力学性能6、材料力学主要研究( )。

A 各种材料的力学问题B 各种材料的力学性能C 杆件受力后变形与破坏的规律D 各类杆中力与材料的关系7、构件的外力包括( )。

A 集中载荷和分布载荷B 静载荷和动载荷C 载荷与约束反力D 作用在物体上的全部载荷第二章杆件的内力分析判断题1、材料力学中的内力是指由外力作用引起的某一截面两侧各质点间相互作用力的合力的改变量。

《工程材料力学性能》（第二版） 《工程材料力学性能》（第二版） 课后答案
第一章
一、 解释下列名词
材料单向静拉伸载荷下的力学性能
滞弹性：在外加载荷作用下，应变落后于应力现象。 静力韧度：材料在静拉伸时单位体积材科从变形到断裂所消耗的功。 弹性极限：试样加载后再卸裁，以不出现残留的永久变形为标准，材料 能够完全弹性恢复的最高应力。 比例极限：应力—应变曲线上符合线性关系的最高应力。 包申格效应：指原先经过少量塑性变形，卸载后同向加载，弹性极限 (ζ P)或屈服强度(ζ S)增加；反向加载时弹性极限(ζ P)或屈服 强度(ζ S)降低的现象。
二、 金属的弹性模量主要取决于什么?为什么说它是一个对结构不敏感的力学 姓能? 答案：金属的弹性模量主要取决于金属键的本性和原子间的结合力，而 材料的成分和组织对它的影响不大，所以说它是一个对组织不敏感的性能指
1
《工程材料力学性能》（第二版）
标，这是弹性模量在性能上的主要特点。改变材料的成分和组织会对材料的 强度(如屈服强度、抗拉强度)有显著影响，但对材料的刚度影响不大。 三、什么是包辛格效应，如何解释，它有什么实际意义? 答案：包辛格效应就是指原先经过变形，然后在反向加载时弹性极限或 屈服强度降低的现象。特别是弹性极限在反向加载时几乎下降到零，这说明 在反向加载时塑性变形立即开始了。 包辛格效应可以用位错理论解释。第一，在原先加载变形时，位错源在 滑移面上产生的位错遇到障碍，塞积后便产生了背应力，这背应力反作用于 位错源，当背应力(取决于塞积时产生的应力集中)足够大时，可使位错源停 止开动。背应力是一种长程(晶粒或位错胞尺寸范围)内应力，是金属基体平 均内应力的度量。因为预变形时位错运动的方向和背应力的方向相反，而当 反向加载时位错运动的方向与原来的方向相反了，和背应力方向一致，背应 力帮助位错运动，塑性变形容易了，于是，经过预变形再反向加载，其屈服 强度就降低了。这一般被认为是产生包辛格效应的主要原因。其次，在反向 加载时， 在滑移面上产生的位错与预变形的位错异号，要引起异号位错消毁， 这也会引起材料的软化，屈服强度的降低。 实际意义：在工程应用上，首先是材料加工成型工艺需要考虑包辛格效 应。其次，包辛格效应大的材料，内应力较大。另外包辛格效应和材料的疲 劳强度也有密切关系，在高周疲劳中，包辛格效应小的疲劳寿命高，而包辛 格效应大的，由于疲劳软化也较严重，对高周疲劳寿命不利。 可以从河流花样的反“河流”方向去寻找裂纹源。 解理断裂是典型的脆性断裂的代表，微孔聚集断裂是典型的塑性断裂。

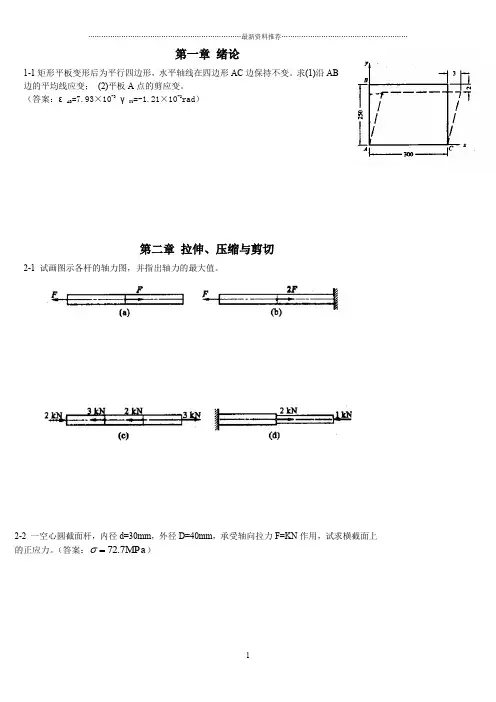
第一章 绪论1-1矩形平板变形后为平行四边形，水平轴线在四边形AC 边保持不变。

求(1)沿AB边的平均线应变； (2)平板A 点的剪应变。

（答案：εAB =7.93×10-3 γXY =-1.21×10-2rad ）第二章 拉伸、压缩与剪切2-1 试画图示各杆的轴力图，并指出轴力的最大值。

2-2 一空心圆截面杆，内径d=30mm ，外径D=40mm ，承受轴向拉力F=KN 作用，试求横截面上的正应力。

（答案：MPa 7.72=σ）2-3 题2－1 c 所示杆，若该杆的横截面面积A=502mm ，试计算杆内的最大拉应力与最大压应力（答案：MPa t 60max ,=σ MPa c 40max ,=σ）2.4图示轴向受拉等截面杆，横截面面积A=5002mm ，载荷F=50KN 。

试求图示截面m-m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。

（答案：MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα）2.6 等直杆受力如图所示，试求各杆段中截面上的轴力，并绘出轴力图。

2.8某材料的应力－应变曲线如图所示，试根据该曲线确定： （1）材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; （2）当应力增加到MPa 350=σ时，材料的正应变ε， 以及相应的弹性应变e ε与塑性应变p ε 2.9图示桁架，杆1与杆2的横截面均为圆形，直径分别为d1=30mm 与d2＝20mm ，两杆材料相2.10图示桁架，杆1为圆截面钢杆，杆2为方截面木杆，在节点A处承受铅垂方向的载荷F作用，试确定钢杆的直径d与木杆截面的边宽b。

已知载荷F=50KN,钢的许用应力[]σ＝160MPa木杆的许用应力[]wσ＝10MPa（答案：d≥20mm，b≥84.1mm）2.11 题2.9所述桁架，试确定载荷F的许用值[]F。

（答案：[]F=97.1KN ）2.12某钢的拉伸试件，直径d=10mm ，标距mm l 500=。

1.自我评价：让学生回顾本节课所学内容，自我评估对知识点的理解和掌握程度。
2.同伴评价：鼓励学生相互评价，分享彼此的学习心得和经验。
3.教师反馈：我会根据学生的表现和作业情况，提供具体的反馈和建议，指出学生的优点和需要改进的地方。
4.改进计划：与学生一起制定个性化的学习计划，帮助他们克服学习中的困难，提高学习效果。
1.通过生活中的实例和实验结果来帮助学生形象地理解抽象概念。
2.指导学生进行实验操作，强调实验数据的准确记录和分析。
3.设计互动环节，提问和讨论，提高学生的参与度。
课后，我将通过学生的作业、实验报告和课堂表现来评估教学效果。具体的反思和改进措施包括：
1.分析学生的作业和报告，找出普遍存在的问题，针对性地进行讲解和辅导。
4.视觉辅助：使用多媒体资源，如动画演示和视频，帮助学生形象地理解摩擦力的作用和变化。
5.互动讨论：在讲解过程中，我会提问并引导学生讨论，以便检查他们对知识的理解和掌握程度。
（三）巩固练习
为了帮助学生巩固所学知识并提升应用能力，我计划设计以下巩固练习和实践活动：
1.实验操作：让学生亲自进行摩擦力实验，记录数据并分析实验结果。
2.根据学生的反馈调整教学方法和内容，以满足不同学生的学习需求。
3.定期进行自我反思，总结教学经验，不断优化教学设计和实施。
3.探究式教学法：引导学生通过提问、假设、验证等步骤，自主探究摩擦力的相关知识，培养科学探究能力。
4.互动讨论法：通过小组讨论，促进学生之间的思维碰撞，提高学生的合作能力和解决问题的能力。
选择这些方法的理论依据是，它们能够充分调动学生的主观能动性，符合学生的认知规律，有助于激发学生的学习兴趣，促进知识的内化和迁移。
（二）教学目标

第一章绪论一、选择题1．根据均匀性假设，可认为构件的（C）在各处相同。

A．应力B．应变C．材料的弹性系数D．位移2．构件的强度是指（C），刚度是指（A），稳定性是指（B）。

A．在外力作用下构件抵抗变形的能力B．在外力作用下构件保持原有平衡状态的能力C．在外力作用下构件抵抗强度破坏的能力3．单元体变形后的形状如下图虚线所示，则A点剪应变依次为图(a) （A），图(b) （C），图(c) （B）。

A．0B．r2C．r D．1.5r4.下列结论中( C )是正确的。

A．内力是应力的代数和；B．应力是内力的平均值；C．应力是内力的集度；D．内力必大于应力；5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力，它们的应力是否相等（B）。

A．不相等；B．相等；C．不能确定；6．为把变形固体抽象为力学模型，材料力学课程对变形固体作出一些假设，其中均匀性假设是指（C）。

A. 认为组成固体的物质不留空隙地充满了固体的体积；B. 认为沿任何方向固体的力学性能都是相同的；C. 认为在固体内到处都有相同的力学性能；D. 认为固体内到处的应力都是相同的。

二、填空题1.材料力学对变形固体的基本假设是连续性假设，均匀性假设，各向同性假设。

2．材料力学的任务是满足强度，刚度，稳定性的要求下，为设计经济安全的构件提供必要的理论基础和计算方法。

3．外力按其作用的方式可以分为 表面力 和 体积力 ，按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。

4．度量一点处变形程度的两个基本量是 （正）应变ε 和 切应变γ。

三、判断题1．因为构件是变形固体，在研究构件平衡时，应按变形后的尺寸进行计算。

（ × ） 2．外力就是构件所承受的载荷。

（ × ） 3．用截面法求内力时，可以保留截开后构件的任一部分进行平衡计算。

（ √ ） 4．应力是横截面上的平均内力。

（ × ） 5．杆件的基本变形只是拉(压)、剪、扭和弯四种，如果还有另一种变形，必定是这四种变形的某种组合。

Microsoft Corporation孙训方材料力学课后答案[键入文档副标题]lenovo[选取日期]第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d)解：。

返回2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：返回2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：返回2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）返回2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此返回2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

′ 的单位是（ B 6．进行轴的刚度计算时，单位轴长的最大扭转角 ϕ max
程中单位轴长的许用扭转角 [ϕ ′] 的单位是（ A ）。 A．（ ° ）/m B．rad/m C．（ ° ） D．rad
），而实际工
7．长度相同、横截面积相同、材料和所受转矩均相同的两根轴，一根为实心轴，一根 为空心轴， ϕ实 和 ϕ空 分别表示实心轴和空心轴的扭转角，则（ B ）。
1
7．当拉（压）杆是等截面时，最大应力必发生在（ B ）的这段杆件内；阶梯形截面 杆某段轴力相同时，最大应力发生在（ A ）的这段杆件内；大截面上作用大轴力、 小截面作用小轴力时，需（ C ）确定最大应力。 A．截面最小 B．最大轴力 C．分别计算 D．不能确定 8．截面相同、轴力相同、材料不同的两拉杆，它们的应力（ C ），强度（ A ）。 A．不相同 B．不一定相同 C．相同 D．无法判断 9．图示两个圆截面杆件的材料相同，受 F 力作用如图，弹 性范围内杆 I 的变形（ C ）。 A．是杆Ⅱ变形的 2 倍 B．小于杆Ⅱ的变形 C．是杆Ⅱ变形的 2.5 倍 D．等于杆Ⅱ的变形 10．低碳钢试件试验中，卸载后重新加载出现冷作硬化的 阶段是（ C ）。 A．弹性阶段；B．屈服阶段；C．强化阶段；D．颈缩阶段。 11．材料呈塑性或脆性是依据（ C ）划分的。 A．比例极限 B．屈服点 C．延伸率 D．强度极限 12．用铸铁制作机器底座、变速箱体等是因为它具有（A、B、C）的优点，适宜制作受 压构件是因为（ D ）。 A．价格低廉、易浇铸成形 B．坚硬耐磨 C．有较好的吸振性 D．抗压性能优良 13．安全因数选取的太小，会使许用应力（ B ），这样会使杆件（ D ）；安全 因数选取的太大，会使许用应力（ A ），这样会使杆件（ C ）。 A．偏低 B．偏高 C．用料多、偏安全 D．用料少、偏危险 14．低碳钢材料拉伸时在屈服阶段沿 45° 斜截面出现滑移线，是由 45° 斜截面上的最大 （ B ）引起的；铸铁材料拉伸时从横截面断裂，是由横截面上的最大（ A ）引起 的；铸铁材料压缩时沿 45° 斜截面断裂，是由 45° 斜截面上的最大（ B ）引起的。 A．正应力 B．切应力 C．相对变形 D．绝对变形 15．两个拉杆轴力相等、截面积相等但截面形状不同，杆件材料不同，则以下结论正确 的是（ C ）。 A．变形相同，应力相同；B．变形相同，应力不同； C．变形不同，应力相同；D．变形不同，应力不同。 16．由①和②两杆组成的支架，从材料性能和经济性两方面考虑，现有低碳钢 和铸铁两种材料可供选择，合理的选择是（ B ）。 A、①杆为铸铁，②杆为铸铁； B、①杆为铸铁，②杆为低碳钢； C、①杆为低碳钢，②杆为铸铁； D、①杆为低 碳钢，②杆为低碳钢。 F 17．图示阶梯形杆， AB 段为钢，BD 段为铝，在外 D 力 F 作用下（ D ）。 A B C Ａ、AB 段轴力最大；Ｂ、BC 段轴力最大； Ｃ、CD 段轴力最大；Ｄ、三段轴力一样大。 18．以下关于图示 AC 杆的结论中，正确的是（ B ）。 A．BC 段有变形，没有位移； B．BC 段没有变形，有位移； C．BC 段没有变形，没有位移；D．BC 段有变形，有位移。

《材料力学性能》课程习题集材料力学性能第一章习题1．解释下列名词：（1）弹性比功；（2）包申格效应；（3）解理面；（4）塑性、脆性和韧性；（5）解理台阶；（6）河流花样；（7）穿晶断裂和沿晶断裂。

2．常用的标准试样有5倍试样和10倍试样，其延伸率分别用σ5和σ10表示，说明为什么σ5>σ10。

3．某汽车弹簧，在未装满载时已变形到最大位置，缺载后可完全恢复到原来状态；另一汽车弹簧，使用一段时间后，发现弹簧弓形越来越小，即产生了塑性变形，而且塑性变形量越来越大。

试分析这两种故障的本质及改变措施。

4、金属的弹性模量主要取决于什么为什么说它是一个对结构不敏感的力学性能5、今有45、40Cr、35CrMo钢和灰铸铁几种材料，你选择那种材料作为机床机身？为什么？6、什么是包辛格效应，如何解释，它有什么实际意义7、产生颈缩的应力条件是什么要抑制颈缩的发生有哪些方法8、为什么材料的塑性要以延伸率这两个指标来度量它们在工程上各有什么实际意义9、试用位错理论解释：粗晶粒不仅屈服强度低，断裂塑性也低；而细晶粒不仅使材料的屈服强度提高，断裂塑性也提高。

10、延性断口有几部分组成？其形成过程如何？11、板材宏观脆性断口的主要特征是什么？如何根据断口特征寻找断裂源？12、简述延性断裂过程中基体和第二相的作用，其形态对材料韧性水平有何关系。

13、由Hall-Petch关系式和解理断裂表达式讨论晶粒尺寸细化在强韧化中的作用。

14、为什么材料发生脆断要先有局部的塑性变形试从理论上给予解释，并从试验上举出一两个实验结果证明上述的论点是正确的。

n15．试证明对可用Hollmon关系S=Kε描述其真应力－真应变关系的材料，其条件抗拉强n度σb＝Ke式中e＝2.71816．一直径为2.5mm，长为200mm的杆，在载荷2000N作用下，直径缩小为2.2mm,试计算：(1)杆的最终长度；(2)在该载荷作用下的真应力S与真应变εe；(3)在该载荷作用下的条件应力σ与条件应变δ。

选择题1.构件在外力作用下（B ）的能力称为稳定性。

A .不发生断裂B .保持原有平衡状态C .不产生变形D.保持静止3 .小变形指的是（C ）二、判断题（正确的打“错的打“X”）1 .材料力学的任务是在保证安全的原则下设计构件。

（X ）2 .构件的强度、刚度和稳定性与所用材料的力学性质有关。

（V ）3 •要使结构安全正常地工作，就必须要求组成它的大部分构件能安全正常地工作。

（X ）4 .任何物体在外力作用下，都会产生变形。

（V ）5 .自然界中的物体分为两类：绝对刚体和变形固体。

（X ）6 .设计构件时，强度越高越好。

（X ）、填空题2.物体受力作用而发生变形,当外力去掉后又能恢复原来形状和尺寸的性质称为A.弹性 B .塑性C .刚性D .稳定性A .构件的变形很小B .刚体的变形C .构件的变形比其尺寸小得多4 .材料力学主要研究（D ）。

A .材料的机械性能 D .构件的变形可以忽略不计B .材料的力学问题C .构件中力与材料的关系D .构件受力后的变形与破坏的规律1•材料力学的任务是研究构件在外力作用下的（变形、受力与破坏或失效）的规律，为合理设计构建提供有关（强度、刚度、稳定性）分析的基本理论和计算方法。

2•构件的强度表示构件（抵抗破坏的）能力；刚度表示构件（抵抗变形的）能力；稳定性表示构件（保持原有平衡形式的）能力。

3•杆件在外力作用下的四种基本变形分别是：（拉压），（剪切），（弯曲），（扭转）。

拉伸与压缩一、选择题（有4个备选答案选出其中一个正确答案。

）1 •若两等直杆的横截面面积为A，长度为I，两端所受轴向拉力均相同，但材料不同，那么下列结论正确的是（B ）。

A•两者轴力不相同 B •两者应变不同C.两者变形不相同 D •两者伸长量相同2.设和!分别表示拉压杆的轴向线应变和横向线应变, 确的是（B）。

A. —B. —C.3.图I-2I表示四种材料的应力一应变曲线，则:（1）弹性模量最大的材料是（A ）;（2）强度最高的材料是（B ）;（3）塑性性能最好的材料是（D ）。

魔术师就能准确地说出推力的作用线落在某两个相邻的小球之间。
魔术师让观众撤去小球后继续表演，观众类似前面方式在任意位置推动木条，只
要说出刚好能推动木条时的推力 F2 ，魔术师就能准确地指出推力位置。
（1）简单说明该魔术可能涉及的力学原理（4 分）。
（2）如何根据滚动小球的号码知道推力作用在哪两个相邻小球之间（12 分）？
（1）求组合截面中性轴的位置（6 分）。
（2）求使梁 B 端下表面刚好接触 D 台面所需的力 FP （8 分）。
（3）求此时粘接面无相对滑动情况下的剪力（6 分）。 （4）计算梁的剪应力值并画出其沿梁截面高度的分布图（10 分）。
四、令人惊讶的魔术师（20 分）
一根均质细长木条 AB 放在水平桌面上，已知沿着 AB 方向推力为 F1 时刚好能
（1－8）
2 分，可以带入 角度。如果坐 标系选取不 同，或符号不 同，只要正确 即可。下面类 似处理
2分
同时根据系统水平动量守恒，有
u
=
v+n x'y'
cosϕ
−
v+τ x'y'
sin ϕ
联立（1－7），（1－8），（1－9），解出
（1－9） 1 分
v+n x'y'
=
v0
sinϕ(e − cos2 1+ cos2 ϕ
作用。
（1）求作用于圆柱上的扭矩 MT （6 分）。 （2）应用第三强度理论（最大剪应力理论），求在圆柱 B 端同时施加多大的轴向
拉伸应力而不产生屈服（6 分）。 （3）求问题（2）情况下圆柱体的体积改变量（8 分）。
三、顶部增强的悬臂梁（30 分）
有一模量为 E1 的矩形截面悬臂梁 AB ， A 端固定， B 端自由。梁长为 L ，截面 高度为 h1 ，宽度为 b 。梁上表面粘着模量为 E2 = 2E1 的增强材料层，该层高度 h2 = 0.1h1 ，长度和宽度与梁 AB 相同。工作台面 D 距离 B 端下表面高度为 Δ 。在 B 端作用垂直向下的载荷 FP 。不考虑各部分的自重。