资料分析比例化分法

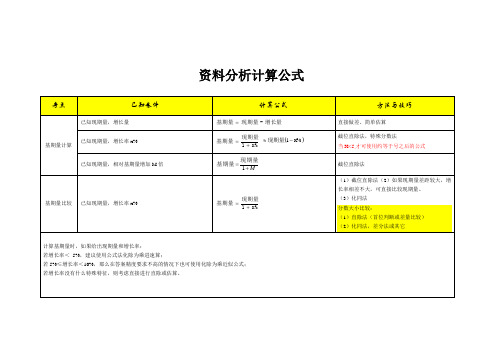
资料分析计算公式
基本概念：
基期：统计中计算指数或变化情况等动态指标时，作为参照标准的时期。

（参照物）现期：相对基期而言，是与基期相比较的后一时期。

同比增长：与上一年同一时期相比的增长情况。

环比增长：与之紧紧相邻的上一个统计周期相比较的增长情况。

贸易顺差与贸易逆差
贸易顺差：进口额< 出口额
贸易顺差= 出口额—进口额
贸易逆差：进口额> 出口额
贸易逆差= 进口额—出口额
年均增长率、年均增长量：
现期量= 基期量()N
⨯，其中n为相差年数；
+
1年均增长率
年均增长量= ()n÷
现期量，其中n为相差年数；
-基期量。

资料分析估算方法 第一节文字资料分析出题方式是：给出一段文字，文字里面含有很多数据，下提出5个问题，考察对文字数据的分析。

文字分析的估算方法有： 1、 多年增长：两个增长率：第一个增长率为r1，第二个增长率为r2，共同的增长率为r1+r2+r1×r2。

比如：第一年的增长率为r1,第二年的增长率为r2，这两年共同的增长率为r1+r2+r1×r2。

再比如：前五年增长率为r1，后五年增长率为r2，这十年的增长率为r1+r2+r1×r2。

多年持续增长：新量＝原量×（1＋r ）年数>原量×（1＋r ×年数），其中r 为增长率，年数表示经过的年份的数量。

（注意：翻几番是原量×2番数，2着区别很大。

）2、三角上溯：增加得快是速率，增长得多是数量，三角上溯是增长率的增量，比如2008年到2009年的增长率为50％，2009年到2010年的增长率为60％，增长率的增长量为10个百分点。

3、总量不同：乘法估算，总量1×比例1－总量2×比例24、定性分析：分子乘以M 大于分母，则此分数>1/M ，反之小于。

比如19/37，有19×2>37，则19/37>1/2。

5、除法估算：资料分析中最重要的估算。

提问有分总（分量和总量）和增减，选项有百分比（％）和数字，按照这4个特征可以把除法分成4个部分：1除估算法：首数法，除出商的前两位数字（最多除到商的第三位），选择答案。

在国考的资料分析中，选项的差异在前两位（最多第三位）就会体现，所以通过判断选项的前两位（最多第三位）就能选出答案。

2除估算法：可以除2次、使用两次首数估算法；也可以把其中的1除化为3除估算法：3除化1除，3除的格式是BA ÷DC ，我们把其中的BA 或者DC 估算成一个简单的分数比如1/2，3/4等等，此时3除就相当于1除了。

资料分析
“细心+速度”
一、分数比大小（分子分母分开比较）
一大一小直接看分子；同大同小看速度
二、运算技巧
1、计算类：看选项截位。

选项差距大（首尾不同或者次位差大于首位）四舍五入留前
两位；选项差距小（其他情况）四舍五入保留前三位。

2、截谁：少步计算一般只截分母；多步计算建议上下都截；
三、增长量的问题：
现期增长量=基期增长量*（1+r）r为增长率
基期增长量=现期增长量/（1+r）r可正可负，当r绝对值<5% 时
r为正值时，则基期增长量=现期增长量*（1-r）（增长）
r为负值时，则基期增长量=现期增长量*（1+r）（降低）
间隔增长率:
隔一年：r=R1+R2+R1*R2
知识点链接：
1、十二五：2011年---2015年；
2、是n倍与增长r倍n=r+1 r=n-1
3、基尼系数：基于0-1之间，系数越大，说明年收入分配越不平均；
4、恩格尔系数：食品支出占总支出的比例，比例越低，反应人民生活水平越高；
5、成数：成数相当于十分之几，
6、翻番：翻一番为2倍，翻两番为4倍，翻n番为原来的2的n次方倍；
7、顺差=出口-进口=出超逆差=进口-出口=入超
1。

增长率一般增长率题型特征……的增长率/增速/增幅是……增长最快/最慢的是……增长+百分数基础公式1--基期现期基期基期现期增长率==解题方法：计算：代入公式（截位直除） 比较：直接比较：基期现期混合增长率题型特征 资料给出各部分的增长率与现期量，求总体增长率解题方法：口诀：混合之后居中，偏向基数更大的一边。

（线段法计算）间隔增长率题型特征求间隔一年的增长率解题方法：代入公式：2121r r r r r ⨯++=间隔年均增长率题型特征求一段时间内的年均增长率基础公式：末期值=年均增长均+1初期值n）（⨯解题方法：计算：代入公式；计算量大时，可居中代入比较：只需比较末期值与初期值的比值增长量题型特征增长了……+单位增长最多/最少的是……基本公式增长量=现期-基期增长率增长率现期增长量⨯+=1解题方法计算：代入公式（尾数法，百分数化分数法）比较：直接比较“现期*增长率”基期与现期普通基期公式：基期=现期-增长量 r 1+=现期基期计算方法：r 大，截位直除r 小，化除为乘间隔基期 公式：间隔现期基期r 1+=2121r r r r r ⨯++=间隔 计算方法：r 间隔大，截位直除r 间隔小，化除为乘基期和差在求基期的基础上进心出差和求和常用方法：截位直除法，估算法，排除选项法现期计算增长量不变：n 基期⨯+=增长量现期增长率不变：n r 1）（基期现期+⨯=比例关系现期比例 公式：BA现期倍数A 是B 的多少倍，A 与B 的比值是多少区别：A 比B 多多少倍（A 比B 增长了多少倍）现期比重A 占B 的比重是多少现期平均数问题中常含有“平均”“均”“每”等关键词基期比例注意与现期比例的区别：基期比例所求比例时间在资料所给数据之间 公式：a 1b 1++⨯B A 基期倍数/比重/平均数两期比例 公式：a 1b -a +⨯B A 两期比重增长量（一般小于|a-b|） 两期平均数增长量（一般情况下，若a>b,比例上升；若a<b ，比例下降；若a=b ，比例不变） 公式：b 1b-a + 两期平均数增长率。

其实从解题角度看，做一道材料分析题分三段，第一段是读懂题目，第二是在文章中找到对应的地方，第三列式计算。

就这三段！其中在很多问题上都需要注意的！读题目上：1.要看清楚年份月份，千万要看清楚，不仅是题目的年份要注意，材料里的年份也要注意，例如，表是5年一格的，你当了一年一格，明明是第二季度的，你不能算第一季度的。

一定要看清楚，我的建议是，题目中看到年份月份，圈出来，让自己重视，（下面很多要圈出来的）。

2就是主体要看清楚，是纺织品、纺织品服装、还是纺织品和服装，这是几个概念，主体不一样，答案就完全不一样的，建议划出来，默念。

3。

就是问题的问法，注意“不”字，或下面“错误”的是，请也圈出来，因为考试紧张，经常会慌乱。

我计算的时候很吝啬笔墨的，但这中地方，我喜欢直观，一目了然。

4。

注意提问的单位！经常出现要算千人的，你算出来的确是人。

当然错了，所以，三个字圈出来5。

读题目的时候，扫一下答案，心中有数，算出来大概是什么！也可以判断是不是需要认真计算。

读题目一般10秒到15秒！大家应尽量控制在10秒内，最好是5秒哦。

下面我们讲讲如何在文章中找到题目对应的地方，这个是一个熟练活！我的经验是扫，几段文字一扫就可以。

但如果文章很乱，心情又非常紧张很难扫出来，要镇静！一行一行过，用笔指着，其实这个用笔过一边也是很快的，决得不会超过15秒的，大家要放心，千万不能乱。

扫到了马上就圈出来！读相关资料，读懂后，就进入到最后一个程序，列式计算。

其实上两个都是准备阶段，很多人在上面两个阶段比较乱，漏洞百出，直接导致后面的计算做了无用功，所以基础工作已经一定要做好！！如何真正的基础工作，我觉得你们需要加强练习，我指的加强练习不是你们原来的简单的做题目模式，而是一定要认真的，放好手表，一套一做，然后强迫自己按照我的方法进行练习，准确快速得读懂题目、找到定位！现在时间紧迫了，但还是来得及的！不需要太多套的，做个20*5，也就两、三个小时就够了，每次做完总结下自己出了什么问题。

公事员资料分析常考题型——比重华图教育 蒲婷婷在资料分析试题中，关于“比重”这一概念的考察每一年都有，这种题往往需要通过复杂的计算才能得出准确的答案，这无形中成为广大考生快速做题的“拦路虎”。

因此，本文通过对资料分析这一部份中“比重”这一概念的讲解和不同类型题目做题思路的归纳，来帮忙大伙儿有效的解决这种难题。

关于“比重”这一概念的概念不难明白得，即部份在整体中所占的比例。

可是，围绕这一概念所出的试题类型却比较多，本文要紧介绍一下几种常见题型。

一、现期比重计算及比较【例题1】（2021-北京-131）2020年世界液化天然气贸易量为亿立方米，天然气贸易量为亿立方米。

那么世界液化天然气贸易量占天然气贸易总量的比重为( )。

这道题是一道典型的计算现期比重的题目，文中已知了整体量，又已知了部分量，要计算部份占整体的比例，那么这两个量直接相较就能够够了，即，依照直除法可知首位商2，排除A 、D ，然后利用插值法插入25%，5.87685.242797105.242745.24275.242741<=⨯=，因此，选择C 选项。

【例题2】（2021-山东-109）下表是某市2020年旅行部门要紧财务情形：问以下哪一类旅行部门2020年的经营利润占昔时营业收入的比重最高?( ) A.宾馆、酒店 B.景点 C.旅行社D.其他旅游企业这道题是一道典型的比较比重大小的题目，题中别离已知了四类指标的营业收入和经营利润，第一将这四类依次表示出来：关于A 选项：722581214594，关于B 选项：65931325735，关于C 选项：239717101714，关于D 选项：6342445。

咱们先排除D 选项，因为D 明显是最小的；第二，再排除B ，因为B 选项的分子只有5位，而分母有6位，相较较于A 和C 明显很小。

在A 和C 中，依照直除法取得商的首位，A 选项商的首位是2，C 选项商的首位是4，因此最大值选择C 选项。

★【速算技巧一：估算法】简称约分法★【速算技巧二：直除法】“直除法”是指在比较或者计算较复杂分数时，通过“直接相除”的方式得到商的首位（首一位或首两位），从而得出正确答案的速算方式。

“直除法”在资料分析的速算当中有非常广泛的用途，并且由于其“方式简单”而具有“极易操作”性。

“直除法”从题型上一般包括两种形式：一、比较多个分数时，在量级相当的情况下，首位最大/小的数为最大/小数；二、计算一个分数时，在选项首位不同的情况下，通过计算首位便可选出正确答案。

“直除法”从难度深浅上来讲一般分为三种梯度：一、简单直接能看出商的首位；二、通过动手计算能看出商的首位；三、某些比较复杂的分数，需要计算分数的第二位是否进位答案。

【例1】32409/4103、32895/4701、23955/3413、12894/1831中最小的数是（）。

【解析】32409/4103、23955/3413、12894/1831都比7大，而32895/4701比7小，因此四个数当中最小的数是32895/4701。

【例2】6874.32/760.31、3052.18/341.02、4013.98/447.13、2304.83/259.74中最大的数是（）。

在本节及以后的计算当中由于涉及到大量的估算，因此我们用a+表示一个比a大的数，用a-表示一个比a小的数。

【解析】只有6874.32/760.31比9大，所以四个数当中最大的数是6874.32/760.31。

【例4】5794.1/27591.43、3482.2/15130.87、4988.7/20788.33、6881.3/26458.46中最大的数是（）。

【解析】本题直接用“直除法”很难直接看出结果，我们考虑这四个数的倒数：27591.43/5794.1、15130.87/3482.2、20788.33/4988.7、26458.46/6881.3，利用直除法，它们的首位分别为“4”、“4”、“4”、“3”，所以四个倒数当中26458.46/6881.3最小，因此原来四个数当中6881.3/26458.46最大。

资料分析常见名词与干货：基期和本期基期，表示的是在比较两个时期的变化的时候，用来作比较值（基准值）的时期，该时期的数值通常作为计算过程中的除数或者减数。

本期，相对于基期而言，是当前所处的时期，该时期的数值通常作为计算过程中的被除数或者被减数。

【注】和谁相比，谁做基期。

增长量、增长率（增长速度、增长幅度）增长量，表示的是本期与基期之间的绝对值差异，是一绝对值。

增长率，表示的是末期也基期之间的相对差异，是一相对值。

增长率=增长速度（增速）=增长幅度（增幅）【注】增加（长）最多比较的是增长量增加（长）最快比较的是增长率多少是量；快慢是率同比、环比同比和环比均表示的是两个时期变化情况，但是这两个概念啊比较的基期不同。

同比，指的是本期发展水平与历史同期大发展水平的变化情况，其基期对应的是历史同期。

环比，指的是本期发展水平与上一个统计周期的发展水平的变化情况，其基期对应的是上一个统计周期。

【注】环比经常出现在月份、季度相关问题。

百分数、百分点百分数，表示的是将相比较的基期的数值抽象为100，然后计算出来的数值，用%表示，一般通过数值相除得到，在资料分析题目中通常用在以下情况：①部分在整体中所占的比重；②表示某个指标的增长率或者减少率百分点，表示的是增长率、比例等用百分数表示的指标的变化情况，一般通过百分数相减得到，在资料分析题目中通常用在以下情况：①两个增长率、比例等以百分数表示的数值的差值；②在A拉动B增长几个百分点，这样的表述中。

倍数、翻番倍数，指将对比的基数抽象为1，从而计算出的数值。

翻番，指数量的加倍，如：如果某指标是原来的2倍，则意味着翻了一番；是原来的4倍，则意味着翻了两番，以此类推。

所用的公式为：末期/基期=2N,即翻了N番。

【注】注意，“比XX多N倍”和“是XX的N倍”两种说法的区别。

比XX多N倍，说明是XX的N+1倍。

比重、比值、平均比重：某事物在整体中所占的分量，计算公式为比重=部分/整体*100%比值：两数相比所得的值。

在学习前复习常用的公式： 1.同比增加量 Aa/1+a 2.隔年求增长率 r1+r2+r1r2 3.比重公式模型 A/B *(1+b)/(1+a) 4.乘除转换A/(1+a)=A*(1-a)，a的绝对值<10% 5.比重变化量：A/B* (a-b)/(1+a) 6.比重变化率 (a-b)/(1+b) 问题分类击破 一、资料分析抓年份 去年今年和明年 年份问题是个小问题，但是，千里之堤毁于蚁穴，小细节上更容易出大问题，首先用笔画出年份，务必不要搞错，费了精力和时间，最后由于年份而功亏一篑，实不应该，公考的1分可能决定太多。

二、选项差距看难易 该放弃时就放弃 这是山东2013题目，较之往年，简单很多，一般用选项差距来衡量难易程度。

因为说到怎么算，大家都知道步骤，重要的还是如何很快的选出答案。

选项差距： 1 和2 差距很大，其实1.1和1.2，选项差距也接近10%呢，所以遇到这样的选项是很容易选出的。

比如101题，属于秒杀的题目。

而当遇到161 163 这样的恶心选项是，有时间就算，没时间就选一个走人。

比重问题：求比重、比重变化率、比重变化趋势、 比重变化趋势常考：口诀： 部分>整体，比重上升。

部分<整体，比重下降。

(这里的部分和整体分别指的部分和整体的增长率) 推导过程： 去年：部分A/(1+a) 整体：B/(1+b) 今年：部分A 整体B 去年比重：A(1+b)/B(1+a) 今年比重：A/B ---》到这里就很明显啦解题妙招 1、比较大小： 常规通分 例题：11793/1.302 9848/1.053比较大小 1053----1302 250 9848+250*9=2XXXX>11793 所以右边大于左边 差分法：(应用前提：分子分母都比另一个数小) 3.3 3.8 0.5 --------- ------- -------- (口诀：大就大值大 小就大值小) 1.092 1.163 0.7多 截位法、倍数法不赘述 补充：资料分析中的经典比较大小问题： 1150.9*7.8%/(1+7.8%) 1067.12*15%/(1+15%) 1246.97*10.9%/(1+10.9%) 1067.67*13%/(1+13%) 典型的A*a/(1+a)的形式，首先考虑A*a 2、乘除转换的应用： a=b/(1+X)=b*(1-x) x的绝对值要小于10%才适用 a=b*(1+x)=b/(1-x) 应用乘除转化时，绝对误差和选项误差比较，如果小于选项误差，则可以使用，绝对误差可以以-b*x2来近似估算(x的平方) 举例： 3772÷(1+3.4%)=( )。

资料分析四大速算技巧（一）作者：华图公务员考试研究员李委明李委明提示：“差分法”是在比较两个分数大小时，用“直除法”或者“化同法”等其他速算方式难以解决时可以采取的一种速算方式。

适用形式：两个分数作比较时，若其中一个分数的分子与分母都比另外一个分数的分子与分母分别仅仅大一点，这时候使用“直除法”、“化同法”经常很难比较出大小关系，而使用“差分法”却可以很好地解决这样的问题。

基础定义：在满足“适用形式”的两个分数中，我们定义分子与分母都比较大的分数叫“大分数”，分子与分母都比较小的分数叫“小分数”，而这两个分数的分子、分母分别做差得到的新的分数我们定义为“差分数”。

例如：324/53.1与313/51.7比较大小，其中324/53.1就是“大分数”，313/51.7就是“小分数”，而324-313/53.1-51.7=11/1.4就是“差分数”。

“差分法”使用基本准则——“差分数．．．：．．．”作比较．．．”与．“小分数．．“大分数．．．”代替1、若差分数比小分数大，则大分数比小分数大；2、若差分数比小分数小，则大分数比小分数小；3、若差分数与小分数相等，则大分数与小分数相等。

比如上文中就是“11/1.4代替324/53.1与313/51.7作比较”，因为11/1.4＞313/51.7（可以通过“直除法”或者“化同法”简单得到），所以324/53.1＞313/51.7。

特别注意：一、“差分法”本身是一种“精算法”而非“估算法”，得出来的大小关系是精确的关系而非粗略的关系；二、“差分法”与“化同法”经常联系在一起使用，“化同法紧接差分法”与“差分法紧接化同法”是资料分析速算当中经常遇到的两种情形。

三、“差分法”得到“差分数”与“小分数”做比较的时候，还经常需要用到“直除法”。

四、如果两个分数相隔非常近，我们甚至需要反复运用两次“差分法”，这种情况相对比较复杂，但如果运用熟练，同样可以大幅度简化计算。

202０国考资料分析之比例增长量技巧资料分析一个备受喜爱的科目,喜爱它的原因一方面它共有2０道题目,占的分值比较高，另一方面题目难度较数量关系会简单一些,所以越来越多的小伙伴加入到了争霸资料分析的大军中来.但就算是简单的科目里也有让大家觉得傻傻分不清的模块，那就是比例增长量和比例增长率.多少人多少次在这个题型中迷失了方向,而作为近几年重点考题的它我们怎能放弃让我们一起来揭开它的神秘面纱，看看到底是什么样的题目难住了我们这些高智商。

熟悉概念弯路少一、比例增长量比例增长量,又因其考察的多为平均数形式，又被称之为平均数增长率.脱离不开典型题目特征,即增长量问题,只不过多了一层比例关系在里面.所以想要盘下这个题型，首先就要熟悉题目特征:本题求的是增长量问题求增长量的时候通常都会已知现期量、基期量来进行求解，但是如果此时没有直接给出这些量。

求解为比例形式现期量是一个比例形式,例如若我国GＤP现期量为Ａ,增长率a％,为Ｂ，增长率为b％,则我国人均GDP的增长量为( )公式推导：现期平均数－基期平均数=不仅仅是平均数,只要是比例形式的增长量都可以应用此公式,实际考试中，应用此公式最多的是两期比重升降问题。

二、比例增长率比例增长率,又因其考察的多为平均数形式，又被称之为平均数增长率。

其实还是脱离不开它带有的典型题目特征,即增长率问题,只不过多了一层比例关系在里面.所以想要盘下这个题型，首先就要熟悉题目特征：本题求的是增长率问题求增长率的时候通常都会已知现期量、基期量或者增长量来进行求解,但是如果此时没有直接给出这些量。

求解为比例形式现期量是一个比例形式，例如若我国GDP现期量为Ａ,增长率ａ%，为Ｂ,增长率为b%，则我国人均GＤP的增长率为（）通过上述公式，我们能看出两者的根本区别在于本质上为比例增长量的计算和增长率的计算，所以大家一定要分清题目特征，知识点清晰。

经典例题对比讲解两期比重比较（比例增长量）经典例题【例题1】2021年，我国贸易总额为297２7．6亿美元，同比增长3４．7％。

资料分析百分数估算技巧实例分析百分数的估算是资料分析经常考查的计算核心考点，值得各位考生着重练习。

下面笔者就和同学们一起来探讨下几道国考和联考中常考的资料分析百分数估算问题的快速思路。

【2010年国考题】中国汽车工业协会发布的2009年4月份中国汽车产销数据显示，在其他国家汽车销售进一步疲软的情况下，国内乘用车销量却持续上升，当月销量已达83.1万辆，比3月份增长7.59%，同比增长37.37%。

乘车用细分为基本型乘用车（轿车）、多功能车（MPV）、运动型多用途车（SUN）和交叉型乘用车。

其中，轿车销量比3月份增长8.3%，同比增长33.04%；MPV销量比3月份下降3.54%，同比下降4.05%，SUV销量比3月份19.27%，同比增长速度22.55%；交叉型乘用车销量比3月份增长 3.62%，同比增长70.66%。

轿车、MPV、SUV和交叉型用业销量占4月份乘用车销量占4月份乘用车总销量的比重分别为71%、2%、6%和20%。

【例1】与上年同期相比，2009年4月份乘用车销量约增长了多少万辆？（）A．13．2 B．22．6C．33．1 D．40．4【答案】B【唐颖老师解析】与上年同期相比，2009年4月份乘用车销量增长了83.1-83.1/(1+37.37%)，将37.37%看作1/3，原式化为83.1×1/4，约为20多一点，选B。

遇到37.37%，22.1%，16.4%等这些常见的大于等于10%的百分数时，我们常常将其转化为简单分数参与计算，会大大化简运算式，大幅提高计算的速度和正确率。

我将其命名为“比例转化法”。

下面是常见的百分数与其转化为分数的对照表：常见百分数与分数转化对照表百分数分数百分数分数10% 1/10 23-27% 1/411% 1/9 33.3%左右1/312-13% 1/8 40%左右2/514-15% 1/7 50%左右1/216-18% 1/6 60%左右3/519-22% 1/5 66.7%左右2/3 【例2】2009年3月份轿车销量均为多少万辆？（）A．50 B．54C．59 D．64【答案】B【唐颖老师解析】2009年4月份轿车销量为83.1×71%，约等于80×75%=60。

资料分析四大速算技巧“差分法”是在比较两个分数大小时，用“直除法”或者“化同法”等其他速算方式难以解决时可以采取地一种速算方式.适用形式：两个分数作比较时，若其中一个分数地分子与分母都比另外一个分数地分子与分母分别仅仅大一点，这时候使用“直除法”、“化同法”经常很难比较出大小关系，而使用“差分法”却可以很好地解决这样地问题.基础定义：在满足“适用形式”地两个分数中，我们定义分子与分母都比较大地分数叫“大分数”，分子与分母都比较小地分数叫“小分数”，而这两个分数地分子、分母分别做差得到地新地分数我们定义为“差分数”.例如：与比较大小，其中就是“大分数”，就是“小分数”，而就是“差分数”.“差分法”使用基本准则——“差分数”代替“大分数”与“小分数”作比较：、若差分数比小分数大，则大分数比小分数大；、若差分数比小分数小，则大分数比小分数小；、若差分数与小分数相等，则大分数与小分数相等.文档来自于网络搜索比如上文中就是“代替与作比较”，因为＞（可以通过“直除法”或者“化同法”简单得到），所以＞.特别注意：一、“差分法”本身是一种“精算法”而非“估算法”，得出来地大小关系是精确地关系而非粗略地关系；二、“差分法”与“化同法”经常联系在一起使用，“化同法紧接差分法”与“差分法紧接化同法”是资料分析速算当中经常遇到地两种情形.三、“差分法”得到“差分数”与“小分数”做比较地时候，还经常需要用到“直除法”.四、如果两个分数相隔非常近，我们甚至需要反复运用两次“差分法”，这种情况相对比较复杂，但如果运用熟练，同样可以大幅度简化计算.【例】比较和地大小【解析】运用“差分法”来比较这两个分数地大小关系：大分数小分数－－(差分数)根据：差分数＞小分数因此：大分数＞小分数李委明提示：使用“差分法”地时候，牢记将“差分数”写在“大分数”地一侧，因为它代替地是“大分数”，然后再跟“小分数”做比较.【例】比较和地大小【解析】运用“差分法”来比较这两个分数地大小关系：小分数大分数－－(差分数)根据：差分数＜小分数（此处运用了“化同法”）因此：大分数＜小分数［注释］本题比较差分数和小分数大小时，还可采用直除法，读者不妨自己试试.李委明提示（“差分法”原理）：以例为例，我们来阐述一下“差分法”到底是怎样一种原理，先看下图：上图显示了一个简单地过程：将Ⅱ号溶液倒入Ⅰ号溶液当中，变成Ⅲ号溶液.其中Ⅰ号溶液地浓度为“小分数”，Ⅲ号溶液地浓度为“大分数”，而Ⅱ号溶液地浓度为“差分数”.显然，要比较Ⅰ号溶液与Ⅲ号溶液地浓度哪个大，只需要知道这个倒入地过程是“稀释”还是“变浓”了，所以只需要比较Ⅱ号溶液与Ⅰ号溶液地浓度哪个大即可.【例】比较和地大小【解析】运用“差分法”来比较这两个分数地大小关系：根据：很明显，差分数＜＜小分数因此：大分数＜小分数［注释］本题比较差分数和小分数大小时，还可以采用“直除法”（本质上与插一个“2”是等价地）.【例】下表显示了三个省份地省会城市（分别为、、城）年及其增长情况，请根据表中所提供地数据回答：、两城年哪个更高？、两城所在地省份年量哪个更高？（亿元）增长率占全省地比例城城城【解析】一、、两城年地分别为：＋、＋；观察特征（分子与分母都相差一点点）我们使用“差分法”：＋＋运用直除法，很明显：差分数＝＞＞＋＝小分数，故大分数＞小分数所以、两城年量城更高.二、、两城所在地省份年量分别为：、；同样我们使用“差分法”进行比较：上述过程我们运用了两次“差分法”，很明显：＞，所以＞；因此年城所在地省份量更高.【例】比较×和×地大小【解析】与很相近，与也很相近，因此使用估算法或者截位法进行比较地时候，误差可能会比较大，因此我们可以考虑先变形，再使用“差分法”，即要比较×和×地大小，我们首先比较和地大小关系：根据：差分数＞＞小分数因此：大分数＞小分数变型：×＞×李委明提示（乘法型“差分法”）：要比较×与′×′地大小，如果ａ与ａ＇相差很小，并且ｂ与ｂ＇相差也很小，这时候可以将乘法×与′×′地比较转化为除法′与′地比较，这时候便可以运用“差分法”来解决我们类似地乘法型问题.我们在“化除为乘”地时候，遵循以下原则可以保证不等号方向地不变：“化除为乘”原则：相乘即交叉.直除法”是指在比较或者计算较复杂分数时，通过“直接相除”地方式得到商地首位（首一位或首两位），从而得出正确答案地速算方式.“直除法”在资料分析地速算当中有非常广泛地用途，并且由于其“方式简单”而具有“极易操作”性.“直除法”从题型上一般包括两种形式：一、比较多个分数时，在量级相当地情况下，首位最大小地数为最大小数；二、计算一个分数时，在选项首位不同地情况下，通过计算首位便可选出正确答案.“直除法”从难度深浅上来讲一般分为三种梯度：一、简单直接能看出商地首位；二、通过动手计算能看出商地首位；三、某些比较复杂地分数，需要计算分数地“倒数”地首位来判定答案.【例】中最大地数是（）.【解析】直接相除：＝＋，＝，＝，＝，明显为四个数当中最大地数.【例】、、、中最小地数是（）.【解析】、、都比大，而比小，因此四个数当中最小地数是.李委明提示：即使在使用速算技巧地情况下，少量却有必要地动手计算还是不可避免地.【例】、、、中最大地数是（）.【解析】只有比大，所以四个数当中最大地数是.【例】、、、中最大地数是（）.【解析】本题直接用“直除法”很难直接看出结果，我们考虑这四个数地倒数：、、、，利用直除法，它们地首位分别为“4”、“4”、“4”、“3”，所以四个倒数当中最小，因此原来四个数当中最大.【例】阅读下面饼状图，请问该季度第一车间比第二车间多生产多少？（）％【解析】＋，所以选.【例】某地区去年外贸出口额各季度统计如下，请问第二季度出口额占全年地比例为多少？（）第一季度第二季度第三季度第四季度全年出口额（亿元）％【解析】＝＋，其倒数＝＋，所以＝()，所以选.【例】根据下图资料，己村地粮食总产量为戊村粮食总产量地多少倍？（）【解析】直接通过直除法计算÷：根据首两位为*得到正确答案为.李委明提示：计算与增长率相关地数据是做资料分析题当中经常遇到地题型，而这类计算有一些常用地速算技巧，掌握这些速算技巧对于迅速解答资料分析题有着非常重要地辅助作用.两年混合增长率公式：如果第二期与第三期增长率分别为与，那么第三期相对于第一期地增长率为：＋＋×增长率化除为乘近似公式：如果第二期地值为，增长率为，则第一期地值′：′＝＋≈×（）（实际上左式略大于右式，越小，则误差越小，误差量级为）平均增长率近似公式：如果年间地增长率分别为、、……，则平均增长率：≈＋＋＋……（实际上左式略小于右式，增长率越接近，误差越小）求平均增长率时特别注意问题地表述方式，例如：.“从年到年地平均增长率”一般表示不包括年地增长率；.“、、、年地平均增长率”一般表示包括４年地增长率.“分子分母同时扩大缩小型分数”变化趋势判定：中若与同时扩大，则①若增长率大，则扩大②若增长率大，则缩小；中若与同时缩小，则①若减少得快，则缩小②若减少得快，则扩大.＋中若与同时扩大，则①若增长率大，则＋扩大②若增长率大，则＋缩小；＋中若与同时缩小，则①若减少得快，则＋缩小②若减少得快，则＋扩大.多部分平均增长率：如果量与量构成总量“＋”，量增长率为，量增长率为，量“＋”地增长率为，则，一般用“十字交叉法”来简单计算：：：注意几点问题：一定是介于、之间地，“十字交叉”相减地时候，一个在前，另一个在后；.算出来地是未增长之前地比例，如果要计算增长之后地比例，应该在这个比例上再乘以各自地增长率，即′′（）×（＋）（）×（＋）.等速率增长结论：如果某一个量按照一个固定地速率增长，那么其增长量将越来越大，并且这个量地数值成“等比数列”，中间一项地平方等于两边两项地乘积.【例】年某市房价上涨，年房价上涨了，则年地房价比年上涨了（）.【解析】＋＋×≈＋＋×≈，选择.【例】年第一季度，某市汽车销量为台，第二季度比第一季度增长了，第三季度比第二季度增长了，则第三季度汽车地销售量为（）.【解析】＋＋×≈＋＋×＝，×(＋)＝，选择.【例】设年某市经济增长率为，年经济增长率为.则、年，该市地平均经济增长率为多少？（）【解析】≈＋＋，选择.【例】假设国经济增长率维持在％地水平上，要想明年达到亿美元地水平，则今年至少需要达到约多少亿美元？（）【解析】＋≈×（），所以选.［注释］本题速算误差量级在()≈，亿地大约为亿元.【例】如果某国外汇储备先增长％，后减少％，请问最后是增长了还是减少了？（）.增长了.减少了.不变.不确定【解析】×（＋％）×（－％）＝0.99A，所以选.李委明提示：例中虽然增加和减少了一个相同地比率，但最后结果却是减少了，我们一般把这种现象总结叫做“同增同减，最后降低”.即使我们把增减调换一个顺序，最后结果仍然是下降了.李委明提示：“综合速算法”包含了我们资料分析试题当中众多体系性不如前面九大速算技巧地速算方式，但这些速算方式仍然是提高计算速度地有效手段.平方数速算：牢记常用平方数，特别是以内数地平方，可以很好地提高计算速度：、、、、、、、、、、、、、、、、、、尾数法速算：因为资料分析试题当中牵涉到地数据几乎都是通过近似后得到地结果，所以一般我们计算地时候多强调首位估算，而尾数往往是微不足道地.因此资料分析当中地尾数法只适用于未经近似或者不需要近似地计算之中.历史数据证明，国考试题资料分析基本上不能用到尾数法，但在地方考题地资料分析当中，尾数法仍然可以有效地简化计算.错位相加减：×型速算技巧：××；如：××型速算技巧：××÷；如：××型速算技巧：××；如：××型速算技巧：××；如：×乘除以、、地速算技巧：×型速算技巧：×10A÷；÷型速算技巧：÷0.1A×例×÷÷×× 型速算技巧：×100A÷；÷ 型速算技巧：÷0.01A×例×÷÷××型速算技巧：×1000A÷；÷型速算技巧：÷0.001A×例×÷÷×减半相加：×型速算技巧：×÷；例×＋÷＋＝“首数相同尾数互补”型两数乘积速算技巧：积地头＝头×（头）；积地尾尾×尾例：“×27”，首数均为“2”，尾数“3”与“7”地和是“10”，互补所以乘积地首数为×(＋)，尾数为×，即×【例】假设某国外汇汇率以％地平均速度增长，预计年之后地外汇汇率大约为现在地多少倍？（）【解析】（＋％）＝≈＝（）＝≈＝≈＝，选择［注释］本题速算反复运用了常用平方数，并且中间进行了多次近似，这些近似各自只忽略了非常小地量，并且三次近似方向也不相同，因此可以有效地抵消误差，达到选项所要求地精度.【例】根据材料，～月地销售额为（）万元.【解析】－－－－－地尾数为“4”，排除、，又从图像上明显得到，月份地销售额低于月份，选择.［注释］这是地方考题经常出现地考查类型，即使存在近似地误差，本题当中地简单减法得出地尾数仍然是非常接近真实值地尾数地，至少不会离“4”很远.文档来自于网络搜索【行测资料集】：。

第二部分资料分析一、熟记数字转换1∕2=50%=0.51∕3=33%=0.33（2∕3=4∕6=6∕9=0.66）1∕4=25%=0.251∕5=20%=0.21∕6=16%=0.161∕7=14.28%=0.142857 2∕7=28.57%=0.2857143∕7=42.85%=0.428571 4∕7=57.14%=0.5714285∕7=71.42%=0.714285 6∕7=85.71%=0.8571421∕8=12.5%=0.125 3∕8=37.5%=0.3755∕8=62.5%=0.625 7∕8=87.5%=0.8751∕9=11%=0.11 2∕9=22%=0.22 4∕9=44%=0.441∕10=10%=0.11∕11=9%=0.0909 4∕11=36%=0.3636二、熟记公式（1）百分数①去年的产量为a，今年的产量为b，今年的产量比去年高10%，则b－a=10%a（以去年的产量为基准）②去年的产量为a，今年的产量为b，去年的产量比今年低10%，则b－a=10%b（以今年的产量为基准）例：（07国考）2005 年全国专利审查与专利代理业务研讨会宣布，1985 年4 月 1 日至2005 年8 月31 日，我国受理的三类专利申请总量达到258 .5万件，其中前100万件历时15年整，而第二个100 万件历时仅4 年零2 个月：至2005 年8 月31 日．三种专利的授予总量达到140 . 38 万件．1．与1985年4月1日至2000年4月1日间专利申请平均受理时间相比，2000年4月 1 日至2004 年6月1日间专利申请的平均受理时间下降了（）A．64％B．68％C．72％D．82％（2）百分点①两个百分数之差（比重之差）②拉动（经济）增长几个百分点拉动……增长几个百分点=————————×100现期某部分增加值=——————————×基期值例：（08北京）2007年前三季度，A市工业生产保持稳步增长的良好态势。

第一部分基本术语“◆”表示“掌握型术语”。

要求考生对其定义、性质、用法及其变形都能有比较熟练的掌握。

“◇”表示“了解型术语”。

只要求考生对其定义有一个基本的认识与了解即可。

◆百分数量A 占量B的百分比例：A÷B×100%【例】某城市有30 万人口，其中老年人有6万，则老年人占总人口的百分之几？【解】【例】某城市有老年人6 万，占总人口的比例为20%，请问这个城市共有多少人？【解】◆成数几成相当于十分之几【例】某单位有300名员工，其中有60人是党员，则党员占总人数的几成？【解】◆折数几折相当于十分之几【例】某服装原件400 元，现价280 元，则该服装打了几折？【解】【注】◆倍数A 是B 的N 倍，则A＝B×N◆基期（基础时期）、现期（现在时期）如果研究“和2006 年相比较，2007 年的某量发生某种变化”，则年为基期，年为现期；如果研究“和2007 年8 月相比较，2007年9月的某量发生某种变化”，则为基期，为现期。

◆增长量（增量）、减少量（减量）增长量＝现期量－基期量减少量＝基期量－现期量◆增长率（增长幅度、增长速度）增长率＝增长量÷基期量×100%【例】某校去年招生人数2000 人，今年招生人数为2400 人，则今年的增幅为？【解】2400－2000＝400，400÷2000×100%＝25%◆减少率（减少幅度、减少速度）减少率＝减少量÷基期量×100%【例】某校去年招生人数2400人，今年招生人数为1800 人，则今年的减幅为？【解】2400－1800＝600，600÷2400×100%＝25%【注】很明显，“减少率”本质上就是一种未带负号的“增长率”◆百分点和百分数基本类似，但百分点不带百分号！【例】某地去年汽车销售总额比前年增加了8%，今年汽车销售总额比去年增加了13%，则今年汽车销售总额增幅提高了多少个百分点？【解】13%－8%＝5%，增幅提高了5%，即提高了5个百分点。

资料分析第一节：速算技巧1速算技巧1.1加法：高位叠加二位数：55+32：十位5+3=8，个位5+2=7，55+32=87三位数：692+516：在十位、个位中间划线，69+51=120，2+6=8，692+516=12081.2划线减法（1）临界值：314-289：中间插入300，314-300=14，300-289=11，314-289=14+11=25。

（2）划线减法：692-516：百位、十位中间划线，6-5=1，92-16=76，692-516=176。

926-532：如果在百位、十位中间划线，26-32是负数，以不借位为前提，在十位、个位中间划线，92-53=39，6-2=4，926-532=394。

（结果为负，用大数减小数）1.3乘法（1）依托两位数*个位数。

（2）口算：两位数*个位数。

97*2：9*2=18，7*2=14，97*2=194。

2截位直除2.1截谁（1）一步除法：只截分母。

如84364/41763、42864/（1+21%）。

（2）多步除法：分子、分母都截（截完约分）。

如（71774/35881）÷ （12482/47620）。

2.2截几位（1）选项差距大，四舍五入保留两位(+1、-1进行微调，将奇数变为偶数，方便约分)①首位均不同。

例：6762/127.36≈（）。

A.65 B.53 C.47 D.38 答：选项首位均不相同，选项差距大，截两位，转化为6762/13，首位商5，对应 B 项。

②首位相同，但次位差＞首位。

例：6762/127.36≈（）。

A.65 B.53 C.59 D.47 答：B、C 项首位相同，次位差是第二位的差，B、C 项次位差9-3=6＞首位5，选项差距大，截两位，转化为6762/13，首位商5，次位商2，B项最接近。

（2）选项差距小，四舍五入保留三位。

首位相同，且次位差≤首位。

(老老实实算吧)例：6762/127.36≈（）。

A.65 B.53 C.58 D.47 答：B、C 项首位相同，次位差8-3=5=首位5，选项差距小，截三位，转化为6762/127，首位商5，次位商3，对应B项。

资料分析四大速算技巧“差分法”是在比较两个分数大小时，用“直除法”或者“化同法”等其他速算方式难以解决时可以采取的一种速算方式。

适用形式：两个分数作比较时，若其中一个分数的分子与分母都比另外一个分数的分子与分母分别仅仅大一点，这时候使用“直除法”、“化同法”经常很难比较出大小关系，而使用“差分法”却可以很好地解决这样的问题。

基础定义：在满足“适用形式”的两个分数中，我们定义分子与分母都比较大的分数叫“大分数”，分子与分母都比较小的分数叫“小分数”，而这两个分数的分子、分母分别做差得到的新的分数我们定义为“差分数”。

例如：324/53.1与313/51.7比较大小，其中324/53.1就是“大分数”，313/51.7就是“小分数”，而324-313/53.1-51.7=11/1.4就是“差分数”。

“差分法”使用基本准则——“差分数”代替“大分数”与“小分数”作比较：1、若差分数比小分数大，则大分数比小分数大；2、若差分数比小分数小，则大分数比小分数小；3、若差分数与小分数相等，则大分数与小分数相等。

比如上文中就是“11/1.4代替324/53.1与313/51.7作比较”，因为11/1.4＞313/51.7（可以通过“直除法”或者“化同法”简单得到），所以324/53.1＞313/51.7。

特别注意：一、“差分法”本身是一种“精算法”而非“估算法”，得出来的大小关系是精确的关系而非粗略的关系；二、“差分法”与“化同法”经常联系在一起使用，“化同法紧接差分法”与“差分法紧接化同法”是资料分析速算当中经常遇到的两种情形。

三、“差分法”得到“差分数”与“小分数”做比较的时候，还经常需要用到“直除法”。

四、如果两个分数相隔非常近，我们甚至需要反复运用两次“差分法”，这种情况相对比较复杂，但如果运用熟练，同样可以大幅度简化计算。

【例1】比较7/4和9/5的大小【解析】运用“差分法”来比较这两个分数的大小关系：大分数小分数9/5 7/49－7/5－1=2/1(差分数)根据：差分数=2/1＞7/4=小分数因此：大分数=9/5＞7/4=小分数李委明提示：使用“差分法”的时候，牢记将“差分数”写在“大分数”的一侧，因为它代替的是“大分数”，然后再跟“小分数”做比较。