2014小学六年级奥数秋季班
- 格式:docx
- 大小:222.35 KB
- 文档页数:8

鹏程学校2014年秋季班六年级奥数测试题姓名: 得分:一. 计算:(每题3分,共8小题)1、0.142857+x=1.52、4141×54+3751×65+5061×763、211++3211+++43211++++……+2008....43211+++++4、0.1+0.2+0.3+.04+0.5+0.6+0.7+0.85、(1+20021+20041+20061)×(20021+20041+20061+20081)—(1+20021+20041+2006120081)×(20021+20041+20061)6、9.08.07.06.05.04.03.02.01.0911811)(711)(611)(511)(411)(311)(211(++++++++--------))(7、35.12.0433⨯×5.4 8、7.625-631+5.75-183二、填空题(每小题3分,共10小题)1、找规律填空:0.987654,0.98765,0.9877,0.988,____,1.0。
2、在21,52,83,114,115,…这一列数中的第8个数是____。
3、如果A*B=BA AB ⨯-那么1*2-2*3-3*4-….-2002*2003-2003*2004=____。
4、若3a=4b ,5b=6c ,那么a 是c 的____倍。
5、今年,妈妈的年龄是小明年龄的6倍,明年小明的年龄将是妈妈年龄的51,则小明今年____岁。
6、将一个长方形,画一笔最多可画出2部分,画两笔最多可画出四部分,那么画2014笔可将长方形最多分成____部分。
7、一种细菌一天生长一倍,第一天1cm ,第二天2cm ,第三天4cm ,第100天760cm ,问第99天这个细菌____cm 。
8、用20cm 长的铁丝弯成边长是整数的长方形,这样的长方形不止一种,其中面积最大的是____c m²,最小的是____c m²。

(★★★)
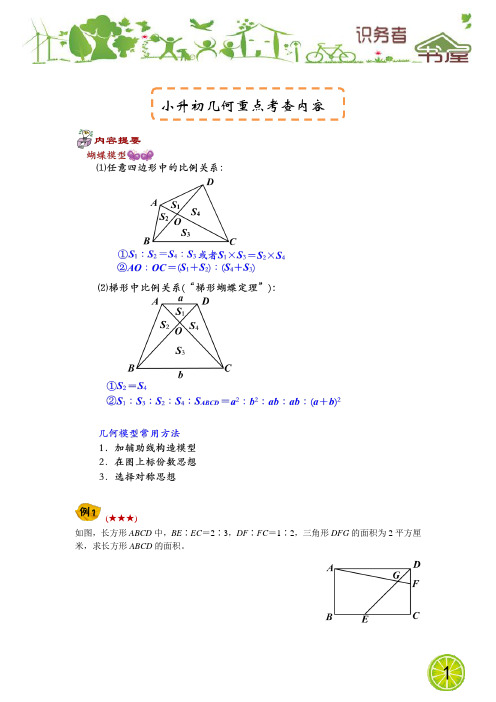
如图,长方形ABCD中,BE∶EC=2∶3,DF∶FC=1∶2,三角形DFG的面积为2平方厘米,求长方形ABCD的面积。
小升初几何重点考查内容
(★★★)
在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是多少平方厘米。
(★★★)
如图,在梯形ABCD中,AD∶BE=4∶3,BE∶EC=2∶3,且△BOE的面积比△AOD的面积小10平方厘米。
梯形ABCD的面积是多少平方厘米?
(★★★)
在三角形ABC中,三角形AEO的面积是1,三角形ABO的面积是2,三角形BOD的面积是3,则四边形DCEO的面积是多少?
(★★★★)
如图,E在AC上,D在BC上,且AE∶EC=2∶3,BD∶DC=1∶2,AD与BE交于点F。
四边形DFEC的面积等于22cm2,则三角形ABC的面积是______。

设数法解题专题简析:在小学数学竞赛中,常常会遇到一些看起来缺少条件的题目,按常规解法似乎无解,但仔细分析就会发现,题目中缺少的条件对于答案并无影响,这时就可以采用“设数代入法”,即对题目中“缺少”的条件,随便假设一个数代入(当然假设的这个数要尽量的方便计算),然后求出解答。
例题1。
如果△△=□□□,△☆=□□□□,那么☆☆□=( )个△。
解: 由第一个等式可以设△=3,□=2,代入第二式得☆=5,再代入第三式左边是12,所以右边括号内应填4。
说明:本题如果不用设数代入法,直接用图形互相代换,显然要多费周折。
练习1已知△=○○□□,△○=□□,☆=□□□,问△□☆=( )个○。
答案 : =8例题2。
足球门票15元一张,降价后观众增加一倍,收入增加15 ,问一张门票降价多少元?【思路导航】初看似乎缺少观众人数这个条件,实际上观众人数于答案无关,我们可以随便假 设一个观众数。
为了方便,假设原来只有一个观众,收入为15元,那么降价后有两个观众,收入为15×(1+15 )=18元,则降价后每张票价为18÷2=9元,每张票降价15-9=6元。
即:15-15×(1+15 )÷2=6(元)说明:如果设原来有a 名观众,则每张票降价:15-15a ×(1+15 )÷2a =6(元)练习2某班一次考试,平均分为70分,其中34 及格,及格的同学平均分为80分,那么不及格的同学平均分是多少分?答案:设考试总人数为4人,70×4-80×3=40(分)小王在一个小山坡来回运动。
先从山下跑上山,每分钟跑200米,再从原路下山,每分钟跑240米,又从原路上山,每分钟跑150米,再从原路下山,每分钟跑200米,求小王的平均速度。
【思路导航】题中四个速度的最小公倍数是1200,设一个单程是1200米。
则(1) 四个单程的和:1200×4=4800(米)(2) 四个单程的时间分别是;1200÷200=6(分)1200÷240=5(分)1200÷150=8(分)1200÷200=6(分)(3) 小王的平均速度为:4800÷(6+5+8+6)=192(米)答:小王的平均速度是每分钟192米。

复习课姓名:日期:【分数应用题篇】1甲数是乙数的23,乙数是丙数的34,甲、乙、丙的和是216,甲、乙、丙各是多少?(找老大型)2 甲数是乙数的23,乙数是丙数的34,丙比甲多16,甲、乙、丙各是多少?(找老大型)3 小黄和大黄同时做180个零件,小黄做的零件数的25等于大黄所做零件的12,求小黄和大黄各做多少个零件?(陈水扁型)4 甲数的23等于乙数的56,丙数是甲数的51,甲、乙、丙三数的和是150,甲、乙、丙三数各是多少?(陈水扁型)5 数学课外兴趣小组,上学期男生占59,这学期增加21名女生后,男生就只占25了,这个小组现有女生多少人?(不变量型)6 有两筐梨,乙筐是甲筐的35,从甲筐取出5千克梨放入乙筐后,乙筐的梨是甲筐的79。
甲、乙两筐梨共重多少千克?(不变量型)7 修一条路,第一天修了全长的25多60米,第二天修的长度比全长的34多35米,已知两天共修555米,这条路全长多少米?(修路型)8 甲、乙、丙、丁四个筑路队共筑1200米长的一段公路,甲队筑的路是其他三个队的13,乙队筑的路是其他三个队的14,丙队筑的路是其他三个队的15,丁队筑了多少米?(修路型)9 钟哲先生从飞机的舷窗向外看去,看见了部分海岛、部分白云以及不大的一块海域,假定白云占窗口画面的一半,它遮住了岛的41,因此岛在窗口画面上只占41。
问:被白云遮住的那部分海洋占画面的多少?10 有一批书,小明9天可装订34,小丽20天可装订56。
小明和小丽两个人合作几天可以装完?(普通型)11 师、徒二人合做一批零件,12天可以完成。
师傅先做了3天,因事外出,由徒弟接着做1天,共完成任务的320。
如果让师傅单独做,多少天可以完成?(分干合想型)12 某工程先由甲单独做45天,再由乙做20天可以完成。
现在甲乙合做30天,就完成了。
如果先由乙单独做30天,再由甲接着做,甲还要工作多少天才能完成?(分干合想型)13 一批零件,甲独做8天完成,乙独做10天完成。

文化教育培训学校小学六年级秋季奥数专题训练十二09年月日学生姓名:家长签字:第一课时一、某车间生产甲、乙两种零件,生产的甲种零件比乙种零件多12个,乙种零件全部合格,甲种零件只有4/5合格,两种零件合格的共有42个,两种零件各生产了多少个?二、某校参加数学竞赛的女生比男生多28人,男生全部得优,女生的3/4得优,男、女生得优的一共有42人,男、女生参加的各有多少人?第二课时一、阅览室看书的学生中,男生比女生多10人,后来男生减少1/4,女生减少1/6,剩下的男、女生人数相等,原来一共有多少名学生在阅览室看书?二、某小学去年参加无线电小组的同学比参加航模小组的同学多5人。
今年参加无线电小组的同学减少1/5,参加航模小组的人数减少1/10,这样,两个组的同学一样多。
去年两个小组各有多少人?第三课时一、甲、乙两个学校共有22人参加竞赛,甲校参加人数的1/5比乙校参加人数的1/4少1人,甲、乙两校各有多少人参加?二、学校图书馆买来文艺书和连环画共126本,文艺书的1/6比连环画的2/9少7本,图书馆买来的文艺书和连环画各是多少本?家庭作业一、有两盒球,第一盒比第二盒多15只,第二盒中全部是红球,第一盒中的2/5是红球,已知红球一共有69个,两盒球共有多少个?二、原来甲、乙两个书架上共有图书900本,将甲书架上的书增加5/8,乙书架上的书增加3/10,这样,两个书架上的书就一样多。
原来甲、乙两个书架上各有图书多少本?三、某校有学生465人,其中女生的2/3比男生的4/5少20人,男女生各多少人?六年级数学上册测试题一、填一填.(28分)1.10:36,读作()。
2.():5=9/15=27÷()=()%=()成。
3.一个正方形的边长为a,边长与周长的比是():(),边长与面积的比是():()。
4.A是8.4,B比A少3.6,A:B=():(),比值是()。
5.一个三角形三个内角度数的比是4:3:2,这三个内角的度数分别是(),(),(),它是()三角形。
第一讲比较分数的大小 (2)第二讲分数运算的技巧 (8)第三讲圆与扇形 (11)第四讲:巧用单位“1” (22)第五讲百分数的应用(一般的百分数问题) (26)第六讲百分数的应用(浓度问题) (30)第七讲百分数的应用(利润问题) (32)第八讲工程问题(一) (36)第九讲工程问题(二) (39)第十讲时钟问题 (42)第十一讲时间问题(二) (45)第十二讲最大最小问题 (48)第十三讲最值问题(二) (50)第十四讲比和比例 (53)第十五讲工程问题(三) (58)第十六讲工程问题(四) (62)第十七讲牛吃草问题 (64)第十八讲加法原理 (67)第十九讲乘法原理 (69)第二十讲立体图形(一) (72)第二十一讲立体图形(二) (76)第二十二讲圆柱与圆锥 (80)第二十三讲不定方程 (85)第一讲比较分数的大小同学们从一开始接触数学,就有比较数的大小问题。
比较整数、小数的大小的方法比较简单,而比较分数的大小就不那么简单了,因此也就产生了多种多样的方法。
对于两个不同的分数,有分母相同,分子相同以及分子、分母都不相同三种情况,其中前两种情况判别大小的方法是:分母相同的两个分数,分子大的那个分数比较大;分子相同的两个分数,分母大的那个分数比较小。
第三种情况,即分子、分母都不同的两个分数,通常是采用通分的方法,使它们的分母相同,化为第一种情况,再比较大小。
由于要比较的分数千差万别,所以通分的方法不一定是最简捷的。
下面我们介绍另外几种方法。
1.“通分子”。
当两个已知分数的分母的最小公倍数比较大,而分子的最小公倍数比较小时,可以把它们化成同分子的分数,再比较大小,这种方法比通分的方法简便。
2、等差比较法如果两个分数的分子分别比各自的分母小相同的数,分子、分母稍大的那个分数比较大。
例如:如果两个分数是假分数,而且分子、分母的差分别相同,那么,分母大的那个分数比较小。
3、相减比较法如果一个分数的分子和分母都比另一个分数的分子和分母大,可把分子的差做分子、分母的差做分母,得到一个新的分数。
刘老师奥数六年级秋季讲义第5讲分数应用题之统一单位“1”在解分数应用题时,常常会出现题中有几个不同的单位“1”,这时需要经过分析将它们转化成统一的单位“1”,然后进行解答。
例题精选例1、庆丰文具店运来的毛笔比钢笔多1000支,其中毛笔的37与钢笔的12支数相同,问庆丰文具店共运来多少支笔?例2、六年级三个班向灾区捐款,六(1)班捐款数是六(2)班和六(3)班捐款总数的23,六(2)班捐款数是六(1)班和六(3)班捐款总数的35,已知六(3)班共捐了180元,求这三个班共捐款多少钱?例3、一棵大树上落着一群鸟,第一次飞走的只数是余下的25,第二次飞走28只,两次飞走的只数比原来的914少2只,这棵树上原来有多少只鸟?例4、有甲、乙两个粮库,原来甲粮库存粮的吨数是乙粮库的57。
如果从乙粮库调6吨粮食到甲粮库,甲粮库存粮的吨数是乙粮库的45。
原来甲、乙粮库各存粮多少吨?例5、有红、黄两种颜色的小球共140个,拿出红球的14,再拿出7个黄球,剩下的红球和黄球正好一样多。
原来红球和黄球各有多少个?例6、某装订车间的三个工人要将一批书打包后送往邮局(要求每包内所装书的本数一样多)。
第一次他们领来这批书的712,结果打了14包还多35本。
第二次他们把剩下的书全部领来了,连同第一次多出来的一起,刚好打了11包。
这批书共有多少本?1、甲、乙两个数之和为180,甲数的14 等于乙数的15 ,甲、乙两个数各是多少?2、兄弟四人合修一条路,结果老大修了另外三人总数的12 ,老二修了另外三人总数的13 ,老三修了另外三人总数的14 ,老四修了91米。
这条路全长多少米?3、某粮店运回一批大米,第一天售出大米总数的42%,第二天售出的大米是第一天的56 ,剩下的大米比第二天售出的大米少324千克,这批大米一共有多少千克?4、甲、乙两桶油共重180千克,把甲桶油的20%倒入乙桶后,甲桶是乙桶的27 ,求甲、乙两桶油原来各有多少千克?5、光明村修一条公路,第一周修了全长的310,如果再修6米,这时已修的米数是未修米数的23 ,这条路全长多少米?6、菜园里西红柿大丰收,收下全部的38 时,装满6筐还多25千克,收完剩余部分后,又刚好装满12筐,这个菜园共收西红柿多少千克?1、食堂原来有的大米和面粉袋数相等,吃掉18袋大米和6袋面粉后,食堂里所剩的大米袋数是面粉的58 ,食堂里原有大米和面粉各多少袋?2、王师傅计划做一批零件,第一天做了计划的47 ,第二天做了余下的35 ,这时还剩下42个零件没做,王师傅计划做多少个零件?3、甲、乙、丙三人共同购买一辆汽车,甲支付的钱是其余两人的411,乙支付的钱是其余两人的23 ,丙支付的钱恰好是10000元。
六年级上册奥数培训教程班级:姓名:【知识要点】1.基本平面图形特征及面积公式2.基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先根据图形的基本关系,再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。
【典型例题】【例1】已知平行四边形的面积是28平方厘米,求阴影部分的面积。
【练一练】如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)特征面积公式正方形①四条边都相等。
②四个角都是直角。
③有四条对称轴。
长方形①对边相等。
②四个角都是直角。
③有二条对称轴。
平行四边形①两组对边平行且相等。
②对角相等,相邻的两个角之和为180°③平行四边形容易变形。
三角形①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是180°。
④有三条边和三个角,具有稳定性。
形①只有一组对边平行。
②中位线等于上下底和的一半。
第一讲巧求图形面积【例2】下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)【练一练】求图中阴影部分的面积。
(单位:厘米)【例3】如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE 的长度。
【练一练】平行四边形ABCD 的边长 BC=10厘米,直角三角形BCE 的直角 边EC 长8厘米,已知阴影部分的面积比 三角形EFG 的面积大10平方厘米。
求CF 的长。
【例4】两条对角线把梯形ABCD 分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:厘米)【练一练】下面的梯形ABCD 中,下底是 上底的2倍,E 是AB 的中点,求梯形ABCD 的面积是三角形EDB 面积的多少倍?【牛刀小试】 1.2.求图中阴影部分的面积。
单位:厘米 B下面的梯形中,阴影部分面积是150平方厘米,求梯形的面积。
3.5.4.梯形ABCD 的面积是45平方厘米,高6厘米。
江西省南昌市2015-2016学年度第一学期期末试卷(江西师大附中使用)高三理科数学分析一、整体解读试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。
试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。
包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。
这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
二、亮点试题分析1.【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点,且满足AB AC →→=,则AB AC →→⋅的最小值为( )A .14-B .12-C .34-D .1-【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识,是向量与三角的典型综合题。
解法较多,属于较难题,得分率较低。
【易错点】1.不能正确用OA ,OB ,OC 表示其它向量。
2.找不出OB 与OA 的夹角和OB 与OC 的夹角的倍数关系。
【解题思路】1.把向量用OA ,OB ,OC 表示出来。
2.把求最值问题转化为三角函数的最值求解。
【解析】设单位圆的圆心为O ,由AB AC →→=得,22()()OB OA OC OA -=-,因为1OA OB OC ===,所以有,OB OA OC OA ⋅=⋅则()()AB AC OB OA OC OA ⋅=-⋅-2OB OC OB OA OA OC OA =⋅-⋅-⋅+ 21OB OC OB OA =⋅-⋅+设OB 与OA 的夹角为α,则OB 与OC 的夹角为2α所以,cos 22cos 1AB AC αα⋅=-+2112(cos )22α=--即,AB AC ⋅的最小值为12-,故选B 。
【举一反三】【相似较难试题】【2015高考天津,理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==则AE AF ⋅的最小值为 .【试题分析】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求,AE AF ,体现了数形结合的基本思想,再运用向量数量积的定义计算AE AF ⋅,体现了数学定义的运用,再利用基本不等式求最小值,体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现. 【答案】2918【解析】因为1,9DF DC λ=12DC AB =,119199918CF DF DC DC DC DC AB λλλλλ--=-=-==, AE AB BE AB BC λ=+=+,19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+,()221919191181818AE AF AB BC AB BC AB BC AB BCλλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥+= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918. 2.【试卷原题】20. (本小题满分12分)已知抛物线C 的焦点()1,0F ,其准线与x 轴的交点为K ,过点K 的直线l 与C 交于,A B 两点,点A 关于x 轴的对称点为D . (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设89FA FB →→⋅=,求BDK ∆内切圆M 的方程. 【考查方向】本题主要考查抛物线的标准方程和性质,直线与抛物线的位置关系,圆的标准方程,韦达定理,点到直线距离公式等知识,考查了解析几何设而不求和化归与转化的数学思想方法,是直线与圆锥曲线的综合问题,属于较难题。
【易错点】1.设直线l 的方程为(1)y m x =+,致使解法不严密。
2.不能正确运用韦达定理,设而不求,使得运算繁琐,最后得不到正确答案。
【解题思路】1.设出点的坐标,列出方程。
2.利用韦达定理,设而不求,简化运算过程。
3.根据圆的性质,巧用点到直线的距离公式求解。
【解析】(Ⅰ)由题可知()1,0K -,抛物线的方程为24y x =则可设直线l 的方程为1x my =-,()()()112211,,,,,A x y B x y D x y -,故214x my y x =-⎧⎨=⎩整理得2440y my -+=,故121244y y m y y +=⎧⎨=⎩则直线BD 的方程为()212221y y y y x x x x +-=--即2222144y y y x y y ⎛⎫-=- ⎪-⎝⎭令0y =,得1214y yx ==,所以()1,0F 在直线BD 上.(Ⅱ)由(Ⅰ)可知121244y y m y y +=⎧⎨=⎩,所以()()212121142x x my my m +=-+-=-,()()1211111x x my my =--= 又()111,FA x y →=-,()221,FB x y →=-故()()()21212121211584FA FB x x y y x x x x m →→⋅=--+=-++=-,则28484,93m m -=∴=±,故直线l 的方程为3430x y ++=或3430x y -+=213y y -===±,故直线BD 的方程330x -=或330x -=,又KF 为BKD ∠的平分线,故可设圆心()(),011M t t -<<,(),0M t 到直线l 及BD 的距离分别为3131,54t t +--------------10分 由313154t t +-=得19t =或9t =(舍去).故圆M 的半径为31253t r +== 所以圆M 的方程为221499x y ⎛⎫-+= ⎪⎝⎭【举一反三】【相似较难试题】【2014高考全国,22】 已知抛物线C :y 2=2px(p>0)的焦点为F ,直线y =4与y 轴的交点为P ,与C 的交点为Q ,且|QF|=54|PQ|.(1)求C 的方程;(2)过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l′与C 相交于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.【试题分析】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,弦长公式的应用,解法及所涉及的知识和上题基本相同. 【答案】(1)y 2=4x. (2)x -y -1=0或x +y -1=0. 【解析】(1)设Q(x 0,4),代入y 2=2px ,得x 0=8p,所以|PQ|=8p ,|QF|=p 2+x 0=p 2+8p.由题设得p 2+8p =54×8p ,解得p =-2(舍去)或p =2,所以C 的方程为y 2=4x.(2)依题意知l 与坐标轴不垂直,故可设l 的方程为x =my +1(m≠0). 代入y 2=4x ,得y 2-4my -4=0. 设A(x 1,y 1),B(x 2,y 2), 则y 1+y 2=4m ,y 1y 2=-4.故线段的AB 的中点为D(2m 2+1,2m), |AB|=m 2+1|y 1-y 2|=4(m 2+1).又直线l ′的斜率为-m ,所以l ′的方程为x =-1m y +2m 2+3.将上式代入y 2=4x ,并整理得y 2+4m y -4(2m 2+3)=0.设M(x 3,y 3),N(x 4,y 4),则y 3+y 4=-4m,y 3y 4=-4(2m 2+3).故线段MN 的中点为E ⎝ ⎛⎭⎪⎫2m2+2m 2+3,-2m ,|MN|=1+1m 2|y 3-y 4|=4(m 2+1)2m 2+1m 2.由于线段MN 垂直平分线段AB ,故A ,M ,B ,N 四点在同一圆上等价于|AE|=|BE|=12|MN|,从而14|AB|2+|DE|2=14|MN|2,即 4(m 2+1)2+⎝ ⎛⎭⎪⎫2m +2m 2+⎝ ⎛⎭⎪⎫2m 2+22=4(m 2+1)2(2m 2+1)m 4,化简得m 2-1=0,解得m =1或m =-1, 故所求直线l 的方程为x -y -1=0或x +y -1=0.三、考卷比较本试卷新课标全国卷Ⅰ相比较,基本相似,具体表现在以下方面: 1. 对学生的考查要求上完全一致。
即在考查基础知识的同时,注重考查能力的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养,既考查了考生对中学数学的基础知识、基本技能的掌握程度,又考查了对数学思想方法和数学本质的理解水平,符合考试大纲所提倡的“高考应有较高的信度、效度、必要的区分度和适当的难度”的原则. 2. 试题结构形式大体相同,即选择题12个,每题5分,填空题4 个,每题5分,解答题8个(必做题5个),其中第22,23,24题是三选一题。
题型分值完全一样。
选择题、填空题考查了复数、三角函数、简易逻辑、概率、解析几何、向量、框图、二项式定理、线性规划等知识点,大部分属于常规题型,是学生在平时训练中常见的类型.解答题中仍涵盖了数列,三角函数,立体何,解析几何,导数等重点内容。
3. 在考查范围上略有不同,如本试卷第3题,是一个积分题,尽管简单,但全国卷已经不考查了。
四、本考试卷考点分析表(考点/知识点,难易程度、分值、解题方式、易错点、是否区分度题)。