求椭圆方程专题练习

椭圆方程与轨迹问题 〖1〗如图,斜线段ΑΒ与平面α所成的角为60,Β为斜足,平面α上的动点Ρ满足30ΡΑΒ∠=,则点Ρ的轨迹是( )A.直线B.抛物线C.椭圆D.双曲线的一支〖2〗如图AB 是长度为定值的平面α的斜线段,点A 为斜足,若点P 在平面α内运动,使得ABP ∆的面积为定值,则动点P 的轨迹是 A.圆 B.椭圆 C 一条直线 D 两条平行线〖3〗已知椭圆C 的方程为22221(0)x y a b a b +=>>,右焦点为(2,0)F ,且离心率为63. 求椭圆C 的方程.〖4〗已知椭圆2222:1(0)x y C a b a b+=>>的离心率为22,且过点(2,1)A .求C 的方程.〖5〗已知椭圆2222:1x y E a b+=(0a b >>)的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线:l 3y x =-+与椭圆E 有且只有一个公共点T .求椭圆E 的方程.〖6〗如图,椭圆2222:1x y E a b+=(0a b >>)的离心率是22,点(0,1)P 在短轴CD 上,且1PC PD ⋅=-.求椭圆E 的方程.〖7〗已知动点(,)M x y 到直线:4l x =的距离是它到点(1,0)N 的距离的2倍. 求动点M 的轨迹C 的方程.〖8〗已知动点P 到直线334-=x的距离是到定点(0,3-)的距离的332倍.求动点P 的轨迹方程.〖9〗动点(,)P x y 满足22(1)(2)|3410|a x y x y -+-=+-，且P 点的轨迹是椭圆，则a 的取值范围是___________________．〖10〗*空间点到平面的距离定义如下:过空间一点作平面的垂线,这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面,,两两互相垂直,点A ∈,点A 到,的距离都是3,点P 是上的动点,满足P 到的距离是P 到点A 距离的2倍,则点P 的轨迹上的点到的距离的最大值是( ) (A) (B) (C)33+ (D)6αβγαβγαβγ33-3〖11〗已知点(2,0)A -,(2,0)B ,动点(,)M x y 满足直线AM 与BM 的斜率之积为12- .记M 的轨迹为曲线C .求C 的方程,并说明C 是什么曲线.〖12〗在平面直角坐标系xOy 中,点B 与点(1,1)A -关于原点O 对称,P 是动点,且直线AP与BP 的斜率之积等于13-.求动点P 的轨迹方程. 〖13〗已知(4,0)M 、(1,0)N ，若动点P 满足||6PN MP MN =⋅.求动点P 的轨迹方程. 〖14〗已知向量(,3),(1,0)a x y b ==，且(3)(3)a b a b +⊥-．求点(,)Q x y 的轨迹C 的方程．〖13〗设Q 、G 分别为ABC ∆的外心和重心,已知)0,1(-A ,)0,1(B ,AB QG //.求点C 的轨迹E .〖14〗在ABC ∆中，两个定点)0,3()0,3(B A -，ABC ∆的垂心H （三角形三条高线的交点）是AB 边上高线CD 的中点.求动点C 的轨迹方程.〖15〗在ABC ∆中,顶点(1,0)B -、(1,0)C ,G 、I 分别是ABC ∆的重心和内心,且IG ∥BC .求顶点A 的轨迹M 的方程.〖16〗已知点(3,0),(3,0)A B -,动圆222:(5)()(0)M x y a a a -+-=≠，分别过A 、B 作动圆M 的切线,两切线（非x 轴）交于点P .求动点P 的轨迹方程.〖17〗设P 是圆2225x y +=上的动点,点D 是P 在x 轴上的投影,M 为线段PD 上一点,且4||||5MD PD =.当P 在圆上运动时,求点M 的轨迹C 的方程. 〖18〗点P 为圆229x y +=上任意一点，过P 作x 轴的垂线，垂足为Q ，点M 在PQ 上，且2PM MQ =，则点M 的轨迹方程为_______________.〖19〗设O 为坐标原点,动点M 在椭圆C 上,过M 作x 轴的垂线,垂足为N ,点P 满足2NP NM =.求点P 的轨迹方程.〖20〗已知B A 、分别是x 轴和y 轴上的两个动点，满足2=AB ，点P 在线段AB 上且PB AP 2=，设点P 的轨迹方程为C ．求曲线C 的方程．〖21〗已知动点A 、B 分别在x 轴、y 轴上，且满足||2AB =，点P 在线段AB 上，且(AP tPB t =是不为零的常数),设点P 的轨迹方程为C .求点P 的轨迹方程C .〖22〗一种画椭圆的工具如图1所示.O 是滑槽AB 的中点,短杆ON 可绕O 转动,长杆MN通过N 处铰链与ON 连接,MN 上的栓子D 可沿滑槽AB 滑动,且1DN ON ==,3MN =.当栓子D 在滑槽AB 内作往复运动时,带动．．N 绕O 转动,M 处的笔尖画出的椭圆记为C .以O 为原点,AB 所在的直线为x 轴建立如图2所示的平面直角坐标系.求椭圆C 的方程.〖23〗△ABC 的两个顶点为(4,0),(4,0)A B -,△ABC 周长为18,则C 点轨迹为( )A.221(0)259x y y +=≠ B. 221(0)259y x y +=≠ C.221(0)169x y y +=≠ D. 221(0)169y x y +=≠ 〖24〗已知A 、B 为坐标平面上的两个定点，且||2AB =，动点P 到A 、B 两点距离之和为常数2，则点P 的轨迹是A.椭圆B.双曲线C.抛物线D. 线段〖25〗已知两个定点1(4,0)F -,2(4,0)F ,且12MF MF +=6, 则点M 的轨迹方程是________.〖26〗已知,sin sin 2sin A B C +=,若点的坐标分别为.求顶点的轨迹的方程. 〖27〗平面直角坐标系中,过椭圆的右焦点作直交于两点,为的中点,且的斜率为.求的方程.〖28〗已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ,过点F 的直线交椭圆于,A B 两点.若AB 的中点坐标为(1,1)-,则E 的方程为 ( ) A.2214536x y += B.2213627x y += C.2212718x y += D.221189x y += 〖29〗已知圆221:(1)16F x y ++=，定点2(1,0)F .动圆M 过点2F ，且与圆1F 相内切.求点M 的轨迹C 的方程.ABC ∆,A B (1,0),(1,0)-C W〖30〗一动圆与圆22650x y x +++=外切,同时与圆226910x y x +--=内切,则动圆圆心的轨迹方程为__________________________. 〖31〗已知圆:,圆:,动圆与外切并且与圆内切,圆心的轨迹为曲线 C.求C 的方程.〖32〗一圆形纸片的半径为10cm ，圆心为,O F 为圆内一定点，6OF cm =，M 为圆周上任意一点，把圆纸片折叠，使M 与F 重合，然后抹平纸片， 这样就得到一条折痕CD ，设CD 与OM 交于P 点(如图)， 建立适当的直角坐标系，求点P 的轨迹方程.〖33〗已知O 为坐标原点，点E 、F 的坐标分别为（2-，0）、（2，0），点A 、N 满足23AE =，12ON OA OF =+（），过点N 且垂直于AF 的直线交线段AE 于点M ，设点M 的轨迹为C ．求轨迹C 的方程．〖34〗如图，在平面直角坐标系中，N 为圆A 16)1(:22=++y x 上的一动点，点(1,0)B ，点M 是BN 中点，点P 在线段AN 上，且.0=⋅BN MP 求动点P 的轨迹方程.〖35〗在周长为定值的△ABC 中,已知||6AB =,且当顶点C 位于定点P 时,cos C 有最小值为.建立适当的坐标系,求顶点C 的轨迹方程. 〖36〗在平面直角坐标系中,长度为6的线段PQ 的一个端点P 在射线0(y x =≤0)上滑动,另一端点Q 在射线0(x y =≤0)上滑动,点M 在线段PQ 上,且.21=MQ PM 求点M 的轨迹方程.〖37〗已知点M ,N 分别在直线y mx =和(0)y mx m =->上运动,点P 是线段MN 的中点,且2,MN =动点P 的轨迹是曲线C .求曲线C 的方程,并讨论C 所表示的曲线类型.〖38〗设A ，B 分别是直线255y x =和255y x =-上的两个动点，并且||20AB =，动点P 满足OP OA OB =+．记动点P 的轨迹为C ．求轨迹C 的方程．257〖39〗过两定点)0,(),0,(a A a A -'，)0(>a 分别作两动直线l l ',，此两动直线在y 轴上的截距分别为t t ',，且2b t t ='（b b ,0>为常数）.求两动直线交点的轨迹C 的方程.〖40〗已知椭圆)0(12222>>=+b a by a x 的左、右焦点分别是1(,0)F c -、2(,0)F c ，Q 是椭圆外的动点，满足.2||1a Q F =点P 是线段1F Q 与该椭圆的交 点，点T 在线段2F Q 上，并且满足.0||,022≠=⋅TF TF PT求点T 的轨迹C 的方程．〖41〗在ABC ∆中，已知(0,1)A ，(0,1)B -，,AC BC 两边所在的直线分别与x 轴交于,E F两点，且OF OE ·＝4．求点C 的轨迹方程． 〖42〗θ取一切实数时，连接(4sin ,6cos )A θθ和(4cos ,6sin )B θθ-两点的线段的中点为M ，点M 的轨迹为______________．〖43〗椭圆141622=+y x 上有两点P 、Q ，若O 为原点，斜率41-=⋅OQ OP K K ，求线段PQ 中点M 的轨迹方程。

椭圆曲线基础练习题本文档将为您提供一些关于椭圆曲线基础知识的练题。

1. 椭圆曲线方程假设给定一个椭圆曲线方程：y^2 = x^3 + ax + b请回答以下问题：a) 比较两个椭圆曲线的方程：y^2 = x^3 + 3x + 2 和 y^2 = x^3 + 2x + 3，它们是否相同？- 是相同的。

两个方程只是常数项 a 和 b 不同，对于椭圆曲线来说，常数项的改变不会影响曲线的形状。

b) 对于方程 y^2 = x^3 + 5x + 7，找出一个曲线上的点。

- 我们需要找到一个满足方程的 (x, y) 值。

可以通过尝试一些整数值来找到一个合适的点，或者使用计算工具辅助计算。

c) 给定一个椭圆曲线方程 y^2 = x^3 + 4x + 5 和一个点 P(2, 3)，求出 P 的相反点 -P。

- 首先，我们需要计算点 P 的 y 坐标的相反数，得到 -y。

然后，将 -y 和 P 的 x 坐标代入原方程计算出 -P 的 x 坐标。

最后，将 -P 的x 和 -y 坐标组合成一个点即可。

2. 点的加法对于椭圆曲线上的点加法，我们使用以下规则：- 如果 P 和 Q 是椭圆曲线上的两个点，它们的和是另一个点 R。

- R 是通过连接 P 和 Q 的直线与椭圆曲线的交点确定的。

请回答以下问题：a) 对于椭圆曲线 y^2 = x^3 + 2x + 3，给定点 P(1, 2) 和 Q(4, 5)，计算出它们的和 R。

- 首先，将 P 和 Q 的坐标代入椭圆曲线方程，求出两个点在曲线上是否成立。

如果两个点在曲线上，我们可以利用点的加法规则进行计算。

b) 如果椭圆曲线上的点 P 和 Q 相同，计算它们的和 R。

- 当两个点相同的时候，我们需要使用椭圆曲线上点的切线与椭圆曲线的交点的方法来计算它们的和。

3. 椭圆曲线的群结构椭圆曲线上的点满足群的结构，有以下特性：- 封闭性：椭圆曲线上的点加法运算结果是椭圆曲线上的点。

- 单位元：椭圆曲线上的点O 是加法的单位元，对于任意点P，P + O = O + P = P。

求椭圆方程真题及答案解析椭圆是数学中一种非常有趣的几何形状，它有着独特的性质和方程表示。

在数学考试中，椭圆方程的求解和解析是一个重要的知识点。

本文将对椭圆方程的真题进行解析，帮助读者更好地理解和掌握这一知识。

在解析椭圆方程之前，我们先来了解一下什么是椭圆方程。

椭圆方程是一种二次方程，一般由以下形式表示：$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$其中，$a$和$b$是椭圆的半长轴和半短轴的长度。

通过调整$a$和$b$的数值，我们可以得到各种不同形状和大小的椭圆。

现在，我们来看一个真实的椭圆方程问题，并进行解析。

题目：已知椭圆$\frac{x^2}{36} + \frac{y^2}{25} = 1$，求解椭圆的焦点坐标和离心率。

解析：首先，我们需要确定椭圆的半长轴和半短轴长度。

根据给定的椭圆方程，可以看出$a=6$和$b=5$，因此半长轴的长度为6，半短轴的长度为5。

然后，我们可以根据椭圆方程的定义来求解焦点坐标。

椭圆的焦点位于椭圆的长轴上，离圆心的距离分别为$c$和$-c$。

根据焦点的性质，我们可以得到以下关系式：$c^2 = a^2 - b^2$将$a=6$和$b=5$代入上述关系式，可以得到$c = \sqrt{6^2 - 5^2} = \sqrt{11}$。

因此，椭圆的焦点坐标为$(\sqrt{11}, 0)$和$(-\sqrt{11}, 0)$。

最后，我们来求解椭圆的离心率。

椭圆的离心率定义为焦点到圆心的距离与半长轴的比值。

根据焦点和半长轴的长度，我们可以得到以下关系式：$e = \frac{c}{a}$将$c = \sqrt{11}$和$a = 6$代入上述关系式，可以得到离心率$e = \frac{\sqrt{11}}{6}$。

至此，我们成功求解了椭圆方程的焦点坐标和离心率。

通过以上的解析过程，我们可以看出，对于椭圆方程的求解和解析，我们需要熟练掌握椭圆的基本性质和方程表示，了解如何根据已知信息求解未知参数，以及如何应用椭圆的定义和性质来解答问题。

(完整word版)椭圆的方程练习题椭圆的方程练题
1. 根据椭圆的定义，椭圆是平面上到两个定点距离之和等于常数的点的集合。

椭圆的标准方程可以表示为：
其中，(h, k)是椭圆的中心坐标，a是椭圆长半轴的长度，b是椭圆短半轴的长度。

2. 练题一：
已知椭圆的中心坐标为(2, 3)，长半轴的长度为4，短半轴的长度为2。

求解该椭圆的方程。

解答：
根据标准椭圆方程的形式，代入已知条件可以得到方程：
即：
3. 练题二：
已知椭圆的方程为:
求解该椭圆的中心坐标以及长半轴和短半轴的长度。

解答：
根据标准椭圆方程的形式，可以得到椭圆的中心坐标为(1, 4)，长半轴的长度为3，短半轴的长度为4。

4. 练题三：
已知椭圆的中心坐标为(-2, 5)，长半轴与短半轴的比值为2。

求解该椭圆的方程。

解答：
假设长半轴的长度为a，短半轴的长度为b，则b/a=1/2。

代入标准椭圆方程可以得到方程：
即：。

椭圆专题（含答案）一、选择题（题型注释）1．椭圆)0(12222>>=+b a by a x 的中心、右焦点、右顶点、右准线与x 轴的交点依次为H A F O ,,,，则OHFA 的最大值为（ ）A ．21 B ．31 C ．41 D ．12．过抛物线24y x =的焦点作直线l 交抛物线于,A B 两点，若线段AB 中点的横坐标为3，则||AB =（ ）A ．10B ．8C ．6D ．43．方程my x ++16m -2522=1表示焦点在y 轴上的椭圆，则m 的取值范围是（ ）A ．-16<m<25B ．-16<m<29 C ．29<m<25 D ．m>29 4．已知点(1,1)A --．若曲线G 上存在两点,B C ，使ABC △为正三角形，则称G 为Γ型曲线．给定下列三条曲线：①3(03)y x x =-+≤≤；②0)y x =≤≤；③1(0)y x x=->．其中，Γ型曲线的个数是（ ）A ．0B ．1C ．2D ．35．过点()1,1M 的直线与椭圆22143x y +=交于,A B 两点, 且点M 平分弦AB ,则直线AB 的方程为（ ）A ．4370x y +-=B ．3470x y +-=C ．3410x y -+=D ．4310x y --=6．已知直线mx ﹣y+1=0交抛物线y=x 2于A 、B 两点，则△AOB （ ）A ．为直角三角形B ．为锐角三角形C ．为钝角三角形D ．前三种形状都有可能 7．与双曲线2222xy -=有共同的渐近线，且过点M （2,-2）的双曲线方程为 .8．已知焦点在x 轴上的椭圆的离心率为,且它的长轴长等于圆C:x 2+y 2-2x-15=0的半径,则椭圆的标准方程是( )(A)+=1 (B)+=1(C)+y 2=1 (D)+=19．已知直线l 交椭圆4x2＋5y2＝80于M ，N 两点，椭圆与y 轴的正半轴交于B 点，若△BMN 的重心恰好落在椭圆的右焦点上，则直线l 的方程是 ( )．A ．6x －5y －28＝0B ．6x ＋5y －28＝0C ．5x ＋6y －28＝0D ．5x －6y －28＝010．已知双曲线C ：22145x y -=的左、右焦点分别为F 1，F 2，P 为C的右支上一点，且|PF 2|＝|F 1F 2|，则12PF PF ⋅等于（ ）A ．24B ．48C ．50D ．5611．在平面坐标系xOy 中，抛物线22y px =的焦点F 与椭圆22162x y +=的左焦点重合，点A 在抛物线上，且||4AF =，若P 是抛物线准线上一动点，则||||PO PA +的最小值为（ ）A ．6B ．2+．．4+12．已知点A 、F 分别是椭圆C ：22221x y a b+=（0a b >>）的上顶点和左焦点，若AF 于圆O ：224x y +=相切于点T ，且点T 是线段AF 靠近点A 的三等分点，则椭圆C 的标准方程为 ． 13．已知双曲线422=-y x ，直线)1(:-=x k y l 与该双曲线只有一个公共点，则k = .(写出所有可能的取值) 14．.给出下列四个命题：（1）方程01222=--+x y x 表示的是圆；（2）动点到两个定点的距离之和为定长，则动点的轨迹为椭圆； （3）点M 与点F(0,-2)的距离比它到直线03:=-y l 的距离小1的 轨迹方程是y x 82-= （4）若双曲线1422=+ky x 的离心率为e ，且21<<e ，则k 的取值范围是()120k ∈-，其中正确命题的序号是__________15．已知双曲线x 2－32y ＝1，过P(2，1)点作一直线交双曲线于A 、B 两点，并使P 为AB 的中点，则直线AB 的斜率为______ 16．过点(0,2)A 可作条直线与双曲线2214y x -=有且只有一个公共点17．点P 在双曲线上•，是这条双曲线的两个焦点，，且的三条边长成等差数列，则此双曲线的离心率是18．已知椭圆的焦点三角形具有“ 椭圆22221x y a b += （0a b >>）的左右焦点分别为12,F F ，点P 为椭圆上任意一点12F PF γ∠=，则椭圆的焦点三角形的面积为122tan2F PF S b γ∆=”；利用由类比推理得出的双曲线的焦点三角形具有的结论，求已 知12,F F 分别是双曲线22221x y a b -=（0,0a b >>）的左、右焦点,过1F 的直线l 与双曲线的左、右两支分别交于,A B 两点．若2ABF 是等边三角形,且c =双曲线的焦点三角形的面积为12F BF S ∆ ．19．若抛物线22y px =的焦点与椭圆22162x y +=的焦点重合，则p 的值为20．给出下列命题：①椭圆12322=+y x 的离心率35=e ，长轴长为32；②抛物线22y x =的准线方程为;81-=x ③双曲线1254922-=-x y 的渐近线方程为x y 75±=；④方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率.其中所有正确命题的序号是21．（理）已知方程x 4+y 2=1，给出下列结论：①它的图形关于x 轴对称；②它的图形关于y 轴对称；③它的图形是一条封闭的曲线，且面积小于π；④它的图形是一条封闭的曲线，且面积大于π.真命题的序号是 .22．已知O 为坐标原点，椭圆C ：)0(12222>>=+b a by a x 的左、右焦点分别为21F F ，，右顶点为A ,上顶点为B , 若|||,||,|2AB OF OB 成等比数列，椭圆C 上的点到焦点2F 的最短距离为26-． （1）求椭圆C 的标准方程；（2）设T 为直线3-=x 上任意一点，过1F 的直线交椭圆C 于点Q P 、，且01=⋅TF ，求||||1PQ TF 的最小值．23．已知椭圆2222:1(0)x y C a b a b +=>>经过点(0,1)，离心率为2．（1）求椭圆C 的方程；（2）设直线:1l x my =+与椭圆C 交于A B 、，点A 关于x 轴的对称点'A （'A 与B 不重合），则直线'A B 与x 轴是否交于一定点？若是，请写出定点坐标，并证明你的结论；若不是，请说明理由． 24．已知椭圆的中心在原点，焦点为F 1()022，-，F 2（0，22），且离心率e =223。

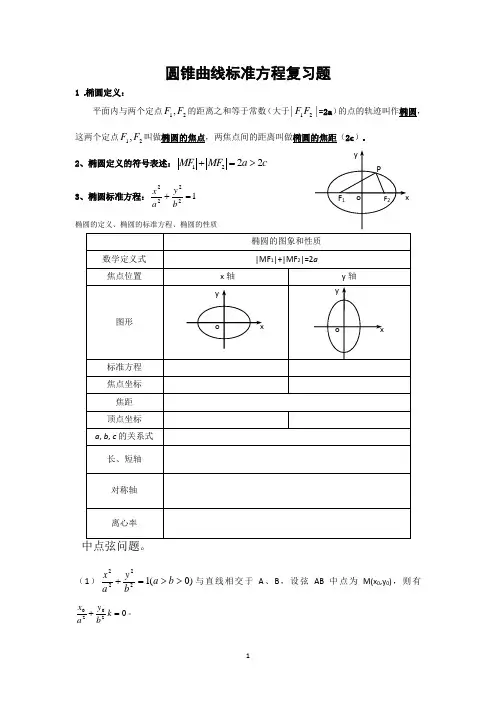
圆锥曲线标准方程复习题1 椭圆定义：平面内与两个定点21,F F 的距离之和等于常数（大于||21F F =2a ）的点的轨迹叫作椭圆，这两个定点21,F F 叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距（2c ）2、椭圆定义的符号表述：1222MF MF a c +=>3、椭圆标准方程：12222=+by a x椭圆的定义、椭圆的标准方程、椭圆的性质（1）)0(12222>>=+b a by a x 与直线相交于A 、B ，设弦AB 中点为M(x 0,y 0)，则有02020=+k by a x 。

（2）)0,0(12222>>=-b a by a x 与直线l 相交于A 、B ，设弦AB 中点为M(x 0,y 0)则有02020=-k by a x （3）y 2=2px （p>0）与直线l 相交于A 、B 设弦AB 中点为M(x 0,y 0),则有2y 0k=2p,即y 0k=p. 一．椭圆专题：1.椭圆两焦点为 1(4,0)F -，2(4,0)F ，P 在椭圆上，若 △12PF F 面积最大值为12，则椭圆方程为（ ）A.221169x y += B . 221259x y += C . 2212516x y += D . 221254x y += 2．焦点在y 轴上，与y 轴的一个交点为P(0，－10)，P 到它较近的一个焦点的距离等于2.求椭圆的标准方程.3.椭圆2214x y +=的两个焦点为12F F ，，过1F 作垂直于x 轴的直线与椭圆相交，一个交点为P ，则2PF 等于4.已知椭圆的方程为18222=+my x ，焦点在x 轴上，则其焦距为（ ） A.228m - B.2m -22 C.282-m D.222-m5.椭圆171622=+y x 的左右焦点为21,F F ，一直线过1F 交椭圆于A 、B 两点，则2ABF ∆的周长为 （ ）6.已知12F 、F p 为椭圆C 上一点，且7. 已知点P 在椭圆1244922=+y x 上，F 1、F 2是椭圆的焦点，且PF 1求（1）| PF 1 |·| PF 2 | （2）△PF 1F 2的面积8. 椭圆1244922=+x y 上一点P 与两个焦点1F 、2F 的连线互相垂直，则△21的面积为（ ）A. 20B. 22C. 28D. 24`9.椭圆1422=+y x 的左右焦点为1F 、2F ， P 是椭圆上一点，当△21PF F 的面积为1时，21PF PF ⋅的值为（ ）A. 0B. 1C. 3D. 610（2012新课标）设1F 、2F 是椭圆E ：2222x y a b +（0a b >>）的左、右焦点，P 为直线32ax =上一点，21F PF ∆是底角为30°的等腰三角形，则E 的离心率为（ ）A ．12 B ．23 C ．34 D ．4511.在ABC △中，AB BC =，7cos 18B =-．若以A B ，为焦点的椭圆经过点C ，则该椭圆的离心率e = ．（2013新课标）12设椭圆C ：12222=+by a x (a ＞b ＞0)的左、右焦点分别为F 1、F 2，P 是C上的点PF 2⊥F 1F 2，∠P F 1F 2=30。

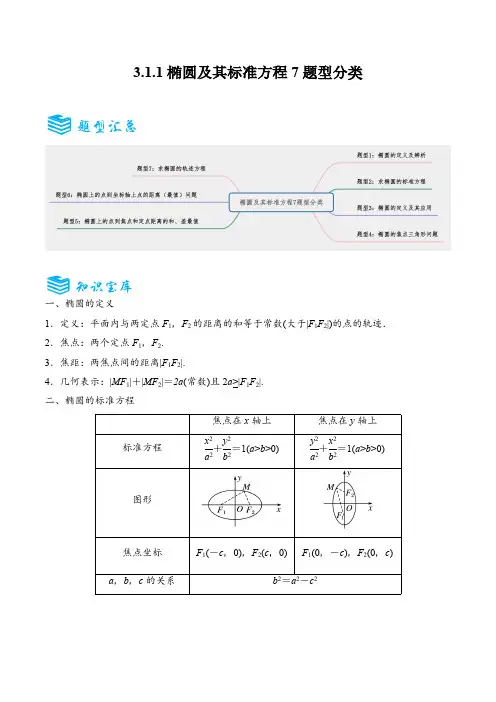
3.1.1椭圆及其标准方程7题型分类一、椭圆的定义1．定义：平面内与两定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹．2．焦点：两个定点F1，F2.3．焦距：两焦点间的距离|F1F2|.4．几何表示：|MF1|＋|MF2|＝2a(常数)且2a>|F1F2|.二、椭圆的标准方程焦点在x轴上焦点在y轴上标准方程x2a2＋y2b2＝1(a>b>0)y2a2＋x2b2＝1(a>b>0)图形焦点坐标F1(－c，0)，F2(c，0)F1(0，－c)，F2(0，c) a，b，c的关系b2＝a2－c2（一）求椭圆的标准方程1.椭圆的定义：平面内与两个定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹．2．椭圆的标准方程焦点在x轴上焦点在y轴上标准方程x2a2＋y2b2＝1(a>b>0)y2a2＋x2b2＝1(a>b>0)图形焦点坐标F1(－c，0)，F2(c，0)F1(0，－c)，F2(0，c) a，b，c的关系b2＝a2－c2（二）椭圆的定义及其应用椭圆定义的应用技巧(1)椭圆的定义能够对椭圆上的点到焦点的距离进行转化．(2)椭圆上一点P与椭圆的两个焦点F1，F2构成的△PF1F2，称为焦点三角形，可以利用椭圆的定义，结合正弦定理、余弦定理、三角形的面积公式等知识求解．(3)椭圆上一点P与椭圆的两焦点F1，F2构成的△F1PF2称为焦点三角形，解关于椭圆中的焦点三角形问题时要充分利用椭圆的定义、三角形中的正弦定理、余弦定理等知识．对于求焦点三角形的面积，若已知∠F1PF2，可利用S＝12ab sin C把|PF1|·|PF2|看成一个整体，利用定义|PF1|＋|PF2|＝2a及余弦定理求出|PF1|·|PF2|，这样可以减少运算量．焦点三角形的常用公式：(1)焦点三角形的周长L＝2a＋2c.(2)在△PF1F2中，由余弦定理可得|F1F2|2＝|PF1|2＋|PF2|2－2|PF1||PF2|cos∠F1PF2.(3)设P(x P，y P)，焦点三角形的面积S△F1PF2＝c|y P|＝12|PF1||PF2|·sin∠F1PF2＝b2tan∠F1PF22.（三）与椭圆有关的轨迹问题求轨迹方程的常用方法(1)直接法设出曲线上动点的坐标为(x，y)后，可根据几何条件直接转换成x，y间的关系式；(2)定义法若动点运动的几何条件满足某种已知曲线的定义，可用待定系数法求出轨迹方程；(3)相关点法(代入法)有些问题中的动点轨迹是由另一动点按照某种规律运动而形成的，只要把所求动点的坐标“转一、单选题1．（2024高二上·福建漳州·期末）点P 在椭圆22:416E x y +=上，12F F 、是E 的两个焦点，若13PF =，则2PF =（ ）A ．5B ．6C ．7D ．82．（2024高二上·福建福州·期中）已知圆()221:125C x y ++=，圆()222:11C x y -+=，动圆M 与圆2C 外切，同时与圆1C 内切，则动圆圆心M 的轨迹方程为（ ）A ．2213x y +=B ．22132x y +=C ．2219x y +=D ．22198x y +=3．（2024高二上·新疆伊犁·期末）如果点(),M x y 在运动过程中，总满足关系式=M 的轨迹是（ ）．A ．不存在B ．椭圆C ．线段D ．双曲线4．（2024高三·全国·专题练习）已知ABC V 的周长为20，且顶点(0,4),(0,4)B C -，则顶点A 的轨迹方程是（ ）A ．221(0)3620x y x +=¹B ．221(0)2036x y x +=¹C ．221(0)620x y x +=¹D ．2212036x y +=5．（2024高二上·四川南充·期末）设定点()10,2F -，()20,2F ，动点P 满足条件125PF PF +=，则点P 的轨迹是（ ）A ．椭圆B ．线段C ．不存在D ．椭圆或线段6．（2024·陕西西安·一模）已知点M 在椭圆221189x y +=上运动，点N 在圆()2211x y +-=上运动，则MN 的最大值为（ ）A ．1B ．1+C ．5D ．67．（2024高二上·全国·课后作业）已知点F 1，F 2是椭圆2222x y +=的左、右焦点，点P 是该椭圆上的一个动点，那么12PF PF +uuu r uuu u r的最小值是（ ）A ．0B ．1C ．2D ．8．（2024高二上·河南信阳·期末）已知1F ，2F 是椭圆C 的两个焦点，P 为C 上一点，122PF PF =，若C，则12F PF Ð=（ ）A ．150°B ．120°C ．90°D ．60°9．（2024高二上·全国·课后作业）设12,F F 分别为椭圆22164x y +=的左右焦点，过1F 的直线交椭圆于A 、B 两点，则2ABF △的周长为（ ）A ．12B ．24C ．D ．10．（2024高二下·河南开封·期末）直线()0R mx y m +=Î与椭圆2251162x y +=交于,A B 两点，则,A B 与椭圆的两个焦点构成的四边形的周长为（ ）A ．10B ．16C ．20D ．不能确定11．（2024·四川南充·一模）已知直线20kx y -+=与椭圆2219x y m+=恒有公共点，则实数m 的取值范围（ ）A ．(]4,9B ．[)4,+¥C ．[)()4,99,¥È+D ．()9,+¥12．（2024高二下·四川南充·阶段练习）方程22123x y m m +=-表示椭圆的一个充分不必要条件是（ ）A ．32m >且3m ¹B ．4m >C ．32m >D ．0m >13．（2024高二上·吉林松原·期末）已知A 为椭圆2212516x y +=上一点，F 为椭圆一焦点，AF 的中点为P ，O为坐标原点，若2OP =则AF =（ ）A ．8B ．6C ．4D ．214．（2024高二上·山东威海·期末）已知椭圆2212y mx +=的焦距为2，则实数m ＝（ ）A ．13B ．16C ．16或12D ．13或115．（2024高二上·吉林·期末）方程222x ky +=表示焦点在x 轴上的椭圆的一个充分但不必要条件是（ ）A ．0k >B ．12k <<C ．1k >D ．01k <<16．（2024高二上·陕西宝鸡·期末）已知椭圆2221(0)9x y C b b +=>：上的动点P 到右焦点距离的最大值为3+则b =（ ）A ．1B C D 17．（2024高三·全国·专题练习）已知椭圆2212516x y +=上一点P 到右准线的距离为10，则点P 到它的左焦点的距离为（ ）A ．4B ．6C ．8D ．1018．（2024·四川南充·模拟预测）已知焦点在y 轴上的椭圆22214x y m+=的焦距等于2，则实数m 的值为（ ）A ．3或5B ．C ．3D ．19．（2024高二上·上海嘉定·12=，化简的结果是（ ）A ．221364x y +=B ．2213632x y +=C ．2213616x y +=D ．2213616y x +=20．（2024高二上·山东·期中）已知椭圆222125x y m+=（0m >）的一个焦点为()10,4F -，则m =（ ）A B ．3C ．41D ．921．（2024高二下·广东汕头·期末）已知椭圆方程221,43x y F +=是其左焦点，点()1,1A 是椭圆内一点，点P是椭圆上任意一点，若PA PF +的最大值为max D ，最小值为min D ，那么max min D D +=（ ）A ．B ．4C ．8D ．22．（2024·辽宁沈阳·三模）已知动点(),P x y 在椭圆22:12516x y C +=上，F 为椭圆C 的右焦点，若点M 满足1MF =uuur 且0MP MF ×=uuu r uuur，则PM uuuu r 的最大值为（ ）A B ．C ．8D ．6323．（2024高三·广西钦州·开学考试）设椭圆C ：22221x y a b +=(a >0，b >0)的左､右焦点分别为1F ，2F ，离心率P 是C 上一点，且1F P ⊥2F P .若12PF F V 的面积为4，则a =A ．1B ．2C ．4D ．824．（2024高二上·河北唐山·期末）已知12,F F 是椭圆22:143x y C +=的左､右焦点，点P 在椭圆C 上.当12F PF Ð最大时，求12PF F S =△（ ）A ．12B C D 25．（2024高二下·四川德阳·阶段练习）椭圆2222:1(0)x y C a b a b +=>>的左，右焦点为12,F F ，且2122b F F a =，点P 是椭圆C 上异于左、右端点的一点，若M 是12PF F V 的内心，且1122MPF MF F MPF S mS S =-△△△，则实数m =（ ）A 2+B 2C ．2D ．226．（2024高二上·广东广州·期末）椭圆2212516x y +=的一个焦点是F ，过原点O 作直线(不经过焦点)与椭圆相交于A ，B 两点，则ABF △的周长的最小值是（ ）A ．14B ．15C ．18D ．2027．（2024高二上·江苏·期中）已知椭圆221167x y +=的右焦点为,F A 是椭圆上一点，点()0,4M ，则AMF V 的周长最大值为（）A ．14B ．16C ．18D ．2028．（2024高二上·河北石家庄·期中）设P 是椭圆2212516x y +=上一点，M ，N 分别是圆221:(3)1C x y ++=和222:(3)4C x y -+=上的点，则PM PN +的最大值为（ ）A ．13B ．10C ．8D ．7二、多选题29．（2024高二上·山东济南·期中）已知曲线22:1C mx ny +=（ ）A ．若0m n >>，则C 是椭圆，其焦点在y 轴上B ．若0m n >>，则C 是椭圆，其焦点在x 轴上C ．若0m n =>，则CD ．若0m =，0n >，则C 是两条直线30．（2024高三·北京·强基计划）已知点(1,1),(1,0)A Q ，P 为椭圆22143x y +=上的动点，则||||PA PQ +的（ ）A ．最大值为4B ．最大值为4C ．最小值为4D ．最小值为4三、填空题31．（2024高二上·全国·课后作业）椭圆221169x y +=上的一点M 到左焦点1F 的距离为2,N 是1MF 的中点，则ON 等于 .32．（2024高二·全国·课后作业）下列命题是真命题的是.(将所有真命题的序号都填上)①已知定点12(1,0),(1,0)F F -，则满足|PF 1|＋|PF 2|P 的轨迹为椭圆；②已知定点F 1(－2，0)，F 2(2，0)，则满足|PF 1|＋|PF 2|＝4的点P 的轨迹为线段；③到定点12(3,0),(3,0)F F -的距离相等的点的轨迹为椭圆.33．（天津市河西区2023-2024学年高二上学期期中数学试题）椭圆22110036x y +=上一点P 与它的一个焦点的距离等于6，那么点P 与另一个焦点的距离等于 .34．（2024·云南红河·模拟预测）已知12,F F 是椭圆2212y x +=的两个焦点，点P 在椭圆上，若12135PF F Ð=°，则点P 到焦点2F 的距离为 ．35．（2024高二下·上海静安·期中）已知P 为椭圆2211612x y +=上一动点，记原点为O ，若2OP OQ =uuu r uuu r ，则点Q 的轨迹方程为 ．36．（2024·上海普陀·二模）设椭圆22:184x y G +=的左、右两焦点分别为1F ，2F ，P 是G 上的点，则使得12PF F V 是直角三角形的点P 的个数为 .37．（2024高二上·陕西宝鸡·期末）已知1F ，2F 是椭圆22:14x C y +=的两个焦点，点M 在C 上，则12MF MF ×的最大值为 ．38．（2024高二下·上海黄浦·期中）设1F 和2F 为椭圆22421x y +=的两个焦点，点P 在椭圆上，且满足12OP =，则12F PF V 的面积是 .39．（2024高二下·江西·开学考试）椭圆2212516x y +=的左右焦点分别为1F ，2F ，P 为椭圆上一点，则12PF F V 面积与12PF F V 周长的比值的最大值为 .40．（2024·河南开封·模拟预测）已知椭圆22195x y +=的左焦点为F ，P 是椭圆上一点，若点()1,1A -，则PA PF +的最小值为 ．41．（2024高二上·天津和平·期中）椭圆2212516x y +=的左、右焦点为F 1､F 2，点P 在椭圆上，若Rt V F 1PF 2，则点P 到x 轴的距离为 .42．（2024高二上·北京朝阳·期中）如图，把椭圆221169x y +=的长轴AB 八等分，过每个分点作x 轴的垂线交椭圆的上半部分于1P ，2P ，L ，7P 七个点，F 是椭圆的一个焦点，则1237PF P F P F P F ++++L 的值为 ．43．（2024高二上·吉林白城·期中）若方程22212x y a a +=+表示焦点在x 轴上的椭圆，则实数a 的取值范围是 .44．（2024·上海静安·二模）已知(1,2)A ，)1B-两点在对称轴为坐标轴的椭圆上，则椭圆的标准方程为 .45．（2024高二·全国·课后作业）“17m <<”是“方程22171x y m m +=--表示的曲线为椭圆”的 条件．46．（2024高二·全国·课后作业）设方程8=；②2=．其中表示椭圆的方程是 ．47．（2024高二上·天津和平·期中）已知椭圆22143x y +=的左、右焦点分别为1F ，2F ，点P 为椭圆上一点，点(4,4)A -，则2||PA PF -的最小值为 ．48．（2024高三·广西柳州·阶段练习）已知F 是椭圆22:143x y C +=的右焦点，P 为椭圆C 上一点，(1,A ，则||||PA PF +的最大值为 ．49．（2024高二上·天津和平·期中）已知12,F F 是椭圆22195y x +=的两个焦点，P 为椭圆上一点，且112PF F F =，则点P 到y 轴的距离为 .50．（2024高二上·全国·课后作业）已知ABC V 的三边a ，b ，c 成等差数列，且a b c >>，A 、C 两点的坐标分别为(1,0),(1,0)-，则顶点B 的轨迹方程为 ．51．（2024高二上·上海宝山·期末）已知P 为椭圆2212516x y +=上的一点，若M N ､分别是圆22(3)3x y ++=和22(3)1x y -+=上的点，则PM PN +的最大值为.52．（2024高三·全国·专题练习）已知点)F ，动点(),M x y 到直线:l x =d ，且d =M 的轨迹为曲线C ．求C 的方程；53．（2024高二·全国·课后作业）已知P 是椭圆221436x y +=上一点，(0,5)A ，求||PA 的最小值与最大值．54．（2024高二·全国·课后作业）已知椭圆以原点为中心，长轴长是短轴长的2倍，且过点()2,4--，求此椭圆的标准方程．。

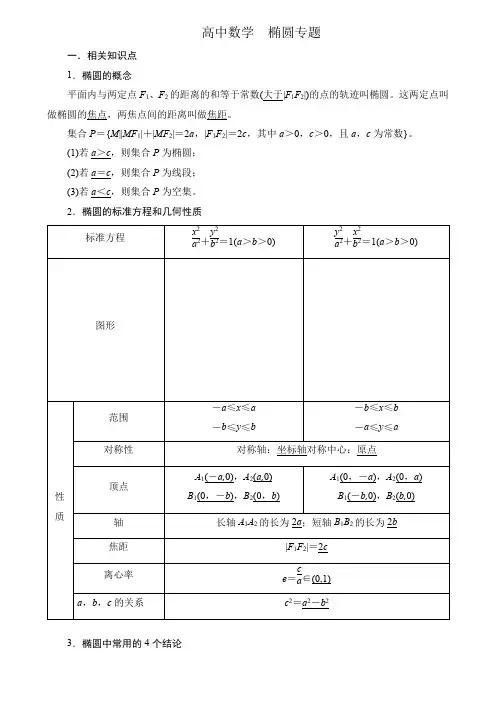
高中数学椭圆专题一．相关知识点1．椭圆的概念平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫椭圆。

这两定点叫做椭圆的焦点，两焦点间的距离叫做焦距。

集合P＝{M||MF1|＋|MF2|＝2a，|F1F2|＝2c，其中a＞0，c＞0，且a，c为常数}。

(1)若a＞c，则集合P为椭圆；(2)若a＝c，则集合P为线段；(3)若a＜c，则集合P为空集。

2．椭圆的标准方程和几何性质3．椭圆中常用的4个结论(1)设椭圆x2a2＋y2b2＝1(a＞b＞0)上任意一点P(x，y)，则当x＝0时，|OP|有最小值b，这时P在短轴端点处；当x＝±a时，|OP|有最大值a，这时P在长轴端点处。

(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形，其中a是斜边长，a2＝b2＋c2。

(3)已知过焦点F1的弦AB，则△ABF2的周长为4a。

(4)若P为椭圆上任一点，F为其焦点，则a－c≤|PF|≤a＋c。

一、细品教材1．(选修1－1P34例1改编)若F1(3,0)，F2(－3,0)，点P到F1，F2距离之和为10，则P点的轨迹方程是()A.x225＋y216＝1 B.x2100＋y29＝1 C.y225＋x216＝1 D.x225＋y216＝1或y225＋x216＝12．(选修1－1P42A组T6改编)设椭圆的两个焦点分别为F1，F2，过F2作椭圆长轴的垂线交椭圆于点P，若△F1PF2为等腰直角三角形，则椭圆的离心率是()A.22 B.2－12C．2－ 2 D.2－1走进教材答案1．A; 2．D 二、双基查验1．设P是椭圆x24＋y29＝1上的点，若F1，F2是椭圆的两个焦点，则|PF1|＋|PF2|等于()A．4B．8 C．6 D．182．方程x25－m＋y2m＋3＝1表示椭圆，则m的范围是()A．(－3,5) B．(－5,3) C．(－3,1)∪(1,5) D．(－5,1)∪(1,3)3．椭圆x 29＋y 24＋k ＝1的离心率为45，则k 的值为( )A ．－21B ．21C ．－1925或21 D.1925或214．已知椭圆的一个焦点为F (1,0)，离心率为12，则椭圆的标准方程为________。

椭圆的标准方程和几何性质练习题一1. 假设曲线ax 2＋by 2＝1为核心在x 轴上的椭圆，那么实数a ，b 知足( )A ．a 2>b 2B.1a <1bC ．0<a <bD ．0<b <a答案：C 由ax 2＋by 2＝1，得x 21a＋y 21b＝1，因为核心在x 轴上，因此1a >1b>0，因此0<a <b . 2. 一个椭圆中心在原点，核心F 1，F 2在x 轴上，P (2,3)是椭圆上一点,且|PF 1|，|F 1F 2|，|PF 2| 成等差数列，那么椭圆方程为( )A.2x 8+2y 6=1B.2x 16+2y 6=1C.2x 8+2y 4=1D.2x 16+2y 4=1 答案：A 设椭圆的标准方程为2222x y a b +=1(a>b>0)。

由点P(2,3)在椭圆上知2243a b+=1。

又|PF 1|，|F 1F 2|，PF 2|成等差数列，那么|PF 1|+|PF 2|=2|F 1F 2|，即2a=2×2c，c 1,a 2=又c 2=a 2-b 2，联立得a 2=8，b 2=6 3. 已知△ABC 的极点B 、C 在椭圆x 23＋y 2＝1上，极点A 是椭圆的一个核心，且椭圆的另外一个核心在BC 边上，那么△ABC 的周长是( )A ．23 B ．6 C ．43 D ．12答案：C 如图，设椭圆的另外一个核心为F ，那么△ABC 的周长为|AB |＋|AC |＋|BC |＝(|AB |＋|BF |)＋(|AC |＋|CF |)＝4a ＝43。

4. 已知椭圆x 2＋my 2＝1的离心率e ∈⎝ ⎛⎭⎪⎫12，1，那么实数m 的取值范围是( )A. ⎝⎛⎭⎫0，34B. ⎝⎛⎭⎫43，＋∞C. ⎝⎛⎭⎫0，34∪⎝⎛⎭⎫43，＋∞ D. ⎝⎛⎭⎫34，1∪⎝⎛⎭⎫1，43答案：C 在椭圆x 2＋my 2＝1中，当0＜m ＜1时，a 2＝1m ，b 2＝1，c 2＝a 2－b 2＝1m－1，∪e 2＝c 2a 2＝1m －11m＝1－m ，又12＜e ＜1，∪14＜1－m ＜1，解得0＜m ＜34，当m ＞1时，a 2＝1，b 2＝1m ，c 2＝1－1m ， e 2＝c 2a 2＝1－1m 1＝1－1m ，又12＜e ＜1，∪14＜1－1m ＜1，解得m ＞43，综上可知实数m 的取值范围是⎝⎛⎭⎫0，34∪⎝⎛⎭⎫43，＋∞。

05椭圆一、典例精析拓思维（名师点拨）核心问题1椭圆的方程例1．（2021·河北·武安市第三中学高二阶段练习）曲线C 的方程是4=，则曲线C 的形状是（）A．圆B．椭圆C．线段D．直线练习1-1．（2021·江西赣州·高二阶段练习（理））已知()()4,0,4,0B C -，且ABC 的周长等于20，求顶点A 的轨迹方程_______.例2．（2021·重庆复旦中学高二期中）（1）已知曲线222()8(:5())C m x m y m R -+-=∈.若曲线C 是焦点在x 轴上的椭圆，求m 的取值范围；（2）求满足下列条件的椭圆的标准方程：经过两点(2,，1,2⎛- ⎝⎭.练习2-1．（2021·全国·高二课时练习）求适合下列条件的椭圆标准方程：（1）经过点()30A -,,()0,2B -；（2）长轴长等于20,焦距等于12.核心问题2椭圆的离心率例1．（2021·北京市第三十五中学高二阶段练习）椭圆()222210x y a b a b +=>>的两顶点为(),0A a ，()0,B b ，左焦点为F ，在FAB 中，90B ∠=︒，则椭圆的离心率为（）C．14练习1-1．（2021·江苏·高二单元测试）已知1F ，2F 分别是椭圆22221(0)x ya b a b+=>>的左，右焦点，若椭圆上存在点P ，使1290F PF ∠=，则椭圆的离心率e 的取值范围为（）A．2⎛ ⎝⎦B．2⎫⎪⎪⎣⎭C．0,2⎛ ⎝⎦D．2⎫⎪⎪⎣⎭练习1-2．（2021·北京医学院附属中学高二期末）椭圆22221(0)x y a b a b+=>>中，点2F 为椭圆的右焦点，点A 为椭圆的左顶点，点B 为椭圆的短轴上的顶点，若2F B AB ⊥，此椭圆称为“黄金椭圆”，“黄金椭圆”的离心率为（）A．2B．12核心问题3焦点三角形例1．（2022·全国·高三专题练习）设12,F F 是椭圆2211224x y +=的两个焦点，P 是椭圆上一点，且1213cos F PF ∠=.则12PF F ∆的面积为（）A．6B．C．8D．练习1-1．（2021·重庆·模拟预测）已知椭圆2222:1(0)x y C a b a b +=>>的右焦点2F 的坐标为()12,0,F 为椭圆C 的左焦点，P 为椭圆上一点，若12124tan ,63PF F F PF S ∠== ，则椭圆C 方程为__________.练习1-2．（2021·黑龙江·哈师大附中高三期中（理））已知点P 是椭圆C ：22221(0)x y a b a b +=>>上一点，点1F ､2F 是椭圆C 的左､右焦点，若12PF F ∆的内切圆半径的最大值为a c -，则椭圆C 的离心率为_________．核心问题4点差法例1．（2022·全国·高三专题练习）已知AB 是椭圆()222210x y a b a b+=>>不垂直于x 轴的任意一条弦，P 是AB 的中点，O 为椭圆的中心.求证：直线AB 和直线OP 的斜率之积是定值.练习1-1．（2022·全国·高三专题练习）过椭圆221164x y +=内的一点(21)M ，引一条弦，使弦被M 点平分，求这条弦所在的直线方程.练习1-2．（2021·浙江省杭州第二中学高二期中）已知椭圆C ：22142x y +=，直线l 与椭圆C 交于,A B 两点，O 为坐标原点.若线段AB 的中点坐标为()1,1，求直线l 的方程：核心问题5椭圆的弦长例1．（2021·全国·高二专题练习）已知点()11,0F -，()21,0F ，动点P 到点1F ，2F 的距离和等于4.（1）试判断点P 的轨迹C 的形状，并写出其方程；（2）若曲线C 与直线:1m y x =-相交于A 、B 两点，求弦AB 的长.练习1-1．（2021·西藏·拉萨那曲第二高级中学高二期末（理））已知椭圆2222:1(0)x y M a b a b +=>>1的直线l 与椭圆M 有两个不同的交点,A B .（1）求椭圆M 的方程；（2）求AB 的最大值.核心问题6椭圆中的面积问题例1．（2021·福建省厦门集美中学高三阶段练习）椭圆2222:1(0)>>x y E a b a b+=的左右焦点分别为1F ，2F ，焦距为O 为原点.椭圆E 上任意一点到1F ，2F 距离之和为（1）求椭圆E 的标准方程；（2）过点(02)P ，的斜率为2的直线l 交椭圆E 于A ､B 两点，求OAB ∆的面积.练习1-1．（2021·江西·南城县第二中学高二阶段练习（理））若椭圆E ：22221(0)x y a b a b+=>>过抛物线24x y =的焦点，且与双曲线221x y -=有相同的焦点.（1）求椭圆E 的方程；（2）不过原点O 的直线l ：y x m =+与椭圆E 交于A ，B 两点，求OAB ∆面积的最大值以及此时直线l 的方程.核心问题7直线与椭圆例1．（2021·江西·南昌大学附属中学高二期中（理））不论k 为何值，直线1y kx =+与椭圆2216x y m+=有公共点，则实数m 的取值范围是（）A．(]0,1B．[)1,+∞C．[)()1,6+∞D．()[)–,01,∞+∞ 例2．（2021·新疆·乌苏市第一中学高二阶段练习）已知点(),P x y 是椭圆22194x y +=上任意一点，则点P 到直线l :5y x =+的最大距离为（）A．2B．2C．D．例3．（2021·陕西·西安高级中学高二期中（理））已知点M 在椭圆C ：2222+=1x y a b ，0a b >>，且椭圆的离心率为3．（1）求椭圆C 的方程：（2）若直线:l y x m =+与椭圆C 交于A ，B 两点，求实数m 的取值范围．二、厚积薄发勤演练（题型归类练）一、单选题1．（2022·重庆·模拟预测）已知椭圆22:15x y C m+=的一个焦点坐标为()2,0，则m =（）A．1B．2C．5D．92．（2022·全国·高三专题练习）如果方程222x ky +=表示焦点在y 轴上的椭圆，那么实数k 的取值范围是（）A．()1,+∞B．()1,2C．1(2，1)D．()0,13．（2022·全国·高三专题练习）已知ABC 的顶点B ，C 在椭圆2213x y +=上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC 边上，则ABC 的周长是（）A．B．6C．4D．4．（2022·全国·高三专题练习（文））如果方程22216x y a a +=+表示焦点在x 轴上的椭圆，则实数a 的取值范围是（）A．()2-∞-，B．(6)(3)-∞-+∞ ，，C．(62)(3)--+∞ ，，D．(3)+∞，5．（2022·全国·高三专题练习）过椭圆22221x y a b+=(0)a b >>的左焦点1F 作x 轴的垂线交椭圆于点P ，2F 为右焦点，若1245F PF ∠=︒，则椭圆的离心率为()A．21-C．16．（2022·全国·高三专题练习）设F 1、F 2是椭圆E ：22221(0)x y a b a b+=>>的左、右焦点，P 为直线32ax =上一点，△F 2PF 1是底角为30°的等腰三角形，则E 的离心率为（）A．14B．2C．34D．127．（2022·全国·高三专题练习）椭圆与双曲线2213y x -=有相同的焦点1F ，2F ，离心率互为倒数，P 为椭圆上任意一点，则角12F PF ∠的最大值为（）A．5π6B．2π3C．π2D．π38．（2022·全国·高三专题练习）已知F 1，F 2分别是椭圆22x a +22y b=1(a >b >0)的左、右焦点，若椭圆上存在点P ，使∠F 1PF 2=90°，则椭圆的离心率e 的取值范围为（）A．0⎛ ⎝⎦B．12⎫⎪⎪⎣⎭C．0⎛ ⎝⎦D．1⎫⎪⎪⎣⎭二、填空题9．（2022·全国·高三专题练习）已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12、F F ，若椭圆上的点P 满足2PF x ⊥轴，122PF PF =，则该椭圆的离心率为___________．10．（2022·全国·高三专题练习）经过椭圆2212x y +=的左焦点1F 作倾斜角为60︒的直线l ，直线l 与椭圆相交于,A B 两点，则线段AB 的长为___________.11．（2022·全国·高三专题练习）已知椭圆22221(0)x y a b a b +=>>的左、右焦点分别为1F 、2F ，关于原点对称的点A 、B 在椭圆上，且满足12||AB F F =，若令1F AB θ∠=且,124ππθ⎡⎤∈⎢⎥⎣⎦，12．（2022·全国·高三专题练习）已知双曲线()2222:10,0x y C a b a b-=>>与椭圆221259x y +=有公共的左､右焦点分别为1F ，2F ，以线段12F F 为直径的圆与双曲线C 及其渐近线在第一象限内分别交于M ，N 两点，且线段1NF 的中点在另一条渐近线上，则2OMF △的面积为___________.三、解答题13．（2022·全国·高三专题练习）已知椭圆C ：22221x y a b+=(a ＞b ＞0)的右焦点F 2与抛物线24y x =的焦点重合，且其离心率为12．（1）求椭圆C 的方程．（2）已知与坐标轴不垂直的直线l 与C 交于M ，N 两点，线段MN 中点为P ，问：MN OP k k ⋅(O 为坐标原点)是否为定值？请说明理由．14．（2022·全国·高三专题练习）已知()()122,0,2,0F F -是椭圆()222210x y a b a b+=>>两个焦点，且2259a b =.（1）求此椭圆的方程；（2）设点P 在椭圆上，且123F PF π∠=，求12F PF △的面积.。

椭圆练习题1A 组 基础过关一、选择题(每小题5分，共25分)1．(2012·厦门模拟)已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率等于 ( )．A.12B.22C. 2D.32解析 由题意得2a ＝22b ⇒a ＝2b ，又a 2＝b 2＋c 2⇒b ＝c ⇒a ＝2c ⇒e ＝22. 答案 B2．(2012·长沙调研)中心在原点，焦点在x 轴上，若长轴长为18，且两个焦点恰好将长轴三等分，则此椭圆的方程是( )． A.x 281＋y 272＝1B.x 281＋y 29＝1C.x 281＋y 245＝1D.x 281＋y 236＝1解析 依题意知：2a ＝18，∴a ＝9,2c ＝13×2a ，∴c ＝3， ∴b 2＝a 2－c 2＝81－9＝72，∴椭圆方程为x 281＋y 272＝1.答案 A3．(2012·长春模拟)椭圆x 2＋4y 2＝1的离心率为( )． A.32 B.34 C.22 D.23解析 先将x 2＋4y 2＝1化为标准方程x 21＋y 214＝1，则a ＝1，b ＝12，c ＝a 2－b 2＝32.离心率e ＝c a ＝32. 答案 A4．(2012·佛山月考)设F 1、F 2分别是椭圆x 24＋y 2＝1的左、右焦点，P 是第一象限内该椭圆上的一点，且PF 1⊥PF 2，则点P 的横坐标为( )． A ．1 B.83 C ．2 2 D.263解析 由题意知，点P 即为圆x 2＋y 2＝3与椭圆x 24＋y 2＝1在第一象限的交点，解方程组⎩⎪⎨⎪⎧x 2＋y 2＝3，x 24＋y 2＝1，得点P 的横坐标为263.答案 D5．(2011·惠州模拟)已知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为32，且椭圆G 上一点到其两个焦点的距离之和为12，则椭圆G 的方程为( )． A.x 24＋y 29＝1 B.x 29＋y 24＝1 C.x 236＋y 29＝1 D.x 29＋y 236＝1解析 依题意设椭圆G 的方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，∵椭圆上一点到其两个焦点的距离之和为12， ∴2a ＝12，∴a ＝6， ∵椭圆的离心率为32. ∴a 2－b 2a ＝32， ∴36－b 26＝32.解得b 2＝9，∴椭圆G 的方程为：x 236＋y 29＝1. 答案 C二、填空题(每小题4分，共12分)6．若椭圆x 225＋y 216＝1上一点P 到焦点F 1的距离为6，则点P 到另一个焦点F 2的距离是________．解析 由椭圆的定义可知，|PF 1|＋|PF 2|＝2a ，所以点P 到其另一个焦点F 2的距离为|PF 2|＝2a －|PF 1|＝10－6＝4. 答案 47．(2011·皖南八校联考)已知F 1、F 2是椭圆C 的左、右焦点，点P 在椭圆上，且满足|PF 1|＝2|PF 2|，∠PF 1F 2＝30°，则椭圆的离心率为________． 解析 在三角形PF 1F 2中，由正弦定理得 sin ∠PF 2F 1＝1，即∠PF 2F 1＝π2，设|PF 2|＝1，则|PF 1|＝2，|F 2F 1|＝3， ∴离心率e ＝2c 2a ＝33. 答案 338．(2011·江西)若椭圆x 2a 2＋y 2b 2＝1的焦点在x 轴上，过点⎝ ⎛⎭⎪⎫1，12作圆x 2＋y 2＝1的切线，切点分别为A ，B ，直线AB 恰好经过椭圆的右焦点和上顶点，则椭圆方程是________．解析 由题可设斜率存在的切线的方程为y －12＝k (x －1)(k 为切线的斜率)， 即2k x －2y －2k ＋1＝0， 由|－2k ＋1|4k 2＋4＝1，解得k ＝－34， 所以圆x 2＋y 2＝1的一条切线方程为3x ＋4y －5＝0， 求得切点A ⎝ ⎛⎭⎪⎫35，45，易知另一切点B (1,0)，则直线AB 的方程为y ＝－2x ＋2. 令y ＝0得右焦点为(1,0)，令x ＝0得上顶点为(0,2)．∴a 2＝b 2＋c 2＝5， 故得所求椭圆方程为x 25＋y 24＝1. 答案 x 25＋y 24＝1 三、解答题(共23分)9．(11分)已知点P (3,4)是椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)上的一点，F 1，F 2是椭圆的两焦点，若PF 1⊥PF 2.试求：(1)椭圆的方程；(2)△PF 1F 2的面积． 解 (1)∵P 点在椭圆上， ∴9a 2＋16b 2＝1.① 又PF 1⊥PF 2，∴43＋c ·43－c ＝－1，得：c 2＝25，②又a 2＝b 2＋c 2，③由①②③得a 2＝45，b 2＝20. 椭圆方程为x 245＋y 220＝1.(2)S △PF 1F 2＝12|F 1F 2|×4＝5×4＝20.10．(12分)(2011·陕西)如图，设P 是圆x 2＋y 2＝25上的动点，点D 是P 在x 轴上的投影，M 为PD 上一点，且|MD |＝45|PD |.(1)当P 在圆上运动时，求点M 的轨迹C 的方程； (2)求过点(3,0)且斜率为45的直线被C 所截线段的长度． 解 (1)设M 的坐标为(x ，y )，P 的坐标为(x P ，y P )， 由已知得⎩⎪⎨⎪⎧x P＝x ，y P ＝54y ，∵P 在圆上，∴x 2＋⎝ ⎛⎭⎪⎫54y 2＝25，即C 的方程为x 225＋y 216＝1.(2)过点(3,0)且斜率为45的直线方程为y ＝45(x －3)， 设直线与C 的交点为A (x 1，y 1)，B (x 2，y 2)， 将直线方程y ＝45(x －3)代入C 的方程，得 x 225＋(x －3)225＝1，即x 2－3x －8＝0. ∴x 1＝3－412，x 2＝3＋412.∴线段AB 的长度为|AB |＝(x 1－x 2)2＋(y 1－y 2)2＝⎝ ⎛⎭⎪⎫1＋1625(x 1－x 2)2＝ 4125×41＝415.B 级 提高题一、选择题(每小题5分，共10分)1．(2012·丽水模拟)若P 是以F 1，F 2为焦点的椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)上的一点，且PF 1→·PF 2→＝0，tan ∠PF 1F 2＝12，则此椭圆的离心率为( )． A.53 B.23 C.13 D.12解析 在Rt △PF 1F 2中，设|PF 2|＝1，则|PF 2|＝2.|F 1F 2|＝5，∴e ＝2c 2a ＝53. 答案 A2．(2011·汕头一模)已知椭圆x 24＋y 22＝1上有一点P ，F 1，F 2是椭圆的左、右焦点，若△F 1PF 2为直角三角形，则这样的点P 有( )． A ．3个 B ．4个 C ．6个 D ．8个解析 当∠PF 1F 2为直角时，根据椭圆的对称性知，这样的点P 有2个；同理当∠PF 2F 1为直角时，这样的点P 有2个；当P 点为椭圆的短轴端点时，∠F 1PF 2最大，且为直角，此时这样的点P 有2个．故符合要求的点P 有6个． 答案 C二、填空题(每小题4分，共8分)3．(2011·镇江调研)已知F 1(－c,0)，F 2(c,0)为椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的两个焦点，P 为椭圆上一点且PF 1→·PF 2→＝c 2，则此椭圆离心率的取值范围是________． 解析 设P (x ，y )，则PF 1→·PF 2→＝(－c －x ，－y )· (c －x ，－y )＝x 2－c 2＋y 2＝c 2①将y 2＝b 2－b 2a 2x 2代入①式解得x 2＝(3c 2－a 2)a 2c 2，又x 2∈[0，a 2]，∴2c 2≤a 2≤3c 2，∴e ＝c a ∈⎣⎢⎡⎦⎥⎤33，22.答案 ⎣⎢⎡⎦⎥⎤33，224．(2011·浙江)设F 1，F 2分别为椭圆x 23＋y 2＝1的左，右焦点，点A ，B 在椭圆上，若F 1A →＝5F 2B →，则点A 的坐标是________．解析 根据题意设A 点坐标为(m ，n )，B 点坐标为(c ，d )．F 1、F 2分别为椭圆的左、右焦点，其坐标分别为(－2，0)、(2，0)，可得F 1A →＝(m ＋2，n )，F 2B →＝(c －2，d )，∵F 1A →＝5F 2B →，∴c ＝m ＋625，d ＝n 5.∵点A 、B 都在椭圆上，∴m 23＋n 2＝1，⎝ ⎛⎭⎪⎫m ＋62523＋⎝ ⎛⎭⎪⎫n 52＝1.解得m ＝0，n ＝±1，故点A 坐标为(0，±1)．答案 (0，±1) 三、解答题(共22分)5．(10分)(2011·大连模拟)设A ，B 分别为椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左，右顶点，⎝ ⎛⎭⎪⎫1，32为椭圆上一点，椭圆长半轴的长等于焦距． (1)求椭圆的方程；(2)设P (4，x )(x ≠0)，若直线AP ，BP 分别与椭圆相交异于A ，B 的点M ，N ，求证：∠MBN 为钝角．(1)解 (1)依题意，得a ＝2c ，b 2＝a 2－c 2＝3c 2，设椭圆方程为x 24c 2＋y 23c 2＝1，将⎝ ⎛⎭⎪⎫1，32代入，得c 2＝1，故椭圆方程为x 24＋y 23＝1.(2)证明 由(1)，知A (－2,0)，B (2,0)，设M (x 0，y 0)，则－2＜x 0＜2，y 20＝34(4－x 20)，由P ，A ，M 三点共线，得x ＝6y 0x 0＋2， BM →＝(x 0－2，y 0)，BP →＝⎝ ⎛⎭⎪⎫2，6y 0x 0＋2， BM →·BP →＝2x 0－4＋6y 20x 0＋2＝52(2－x 0)＞0，即∠MBP 为锐角，则∠MBN 为钝角．6．(★)(12分)(2011·西安五校一模)已知中心在原点，焦点在x 轴上的椭圆C 的离心率为12，且经过点M ⎝ ⎛⎭⎪⎫1，32.(1)求椭圆C 的方程；(2)是否存在过点P (2,1)的直线l 1与椭圆C 相交于不同的两点A ，B ，满足P A →·PB →＝PM →2若存在，求出直线l 1的方程；若不存在，请说明理由． 解 (1)设椭圆C 的方程为x 2a 2＋y2b 2＝1(a ＞b ＞0)，由题意得⎩⎪⎨⎪⎧1a 2＋94b 2＝1，c a ＝12，a 2＝b 2＋c 2，解得a 2＝4，b 2＝3.故椭圆C 的方程为x 24＋y 23＝1.(2)假设存在直线l 1且由题意得斜率存在，设满足条件的方程为y ＝k 1(x －2)＋1，代入椭圆C 的方程得，(3＋4k 21)x 2－8k 1(2k 1－1)x ＋16k 21－16k 1－8＝0.因为直线l 1与椭圆C 相交于不同的两点A ，B ，设A ，B 两点的坐标分别为(x 1，y 1)，(x 2，y 2)，所以Δ＝[－8k 1(2k 1－1)]2－4(3＋4k 21)(16k 21－16k 1－8)＝32(6k 1＋3)＞0，所以k 1＞－12.又x 1＋x 2＝8k 1(2k 1－1)3＋4k 21，x 1x 2＝16k 21－16k 1－83＋4k 21， 因为P A →·PB→＝PM →2，即(x 1－2)(x 2－2)＋(y 1－1)(y 2－1)＝54， 所以(x 1－2)·(x 2－2)(1＋k 21)＝|PM |2＝54. 即[x 1x 2－2(x 1＋x 2)＋4](1＋k 21)＝54.所以⎣⎢⎡⎦⎥⎤16k 21－16k 1－83＋4k 21－2·8k 1(2k 1－1)3＋4k 21＋4(1＋k 21)＝4＋4k 213＋4k 21＝54，解得k 1＝±12. 因为k 1＞－12，所以k 1＝12.于是存在直线l 1满足条件，其方程为y ＝12x .【点评】 解决解析几何中的探索性问题的一般步骤为：,第一步：假设结论成立.,第二步：以存在为条件，进行推理求解.,第三步：明确规范结论，若能推出合理结果，经验证成立即可肯定正确.若推出矛盾，即否定假设.,第四步：回顾检验本题若忽略Δ＞0这一隐含条件，结果会造成两解.椭圆练习题2一、填空题1．椭圆63222=+y x 的焦距为______________。

基础知识：1．椭圆的定义椭圆是平面上到两定点21F F 、距离之和等于常数（大于||21F F ）的点的轨迹，定点21F F 、叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。

若设动点M 到21F F 、距离之和为2a ，c F F 2||21=，则（1）当a>c>0时，动点M 的轨迹是椭圆；（2）当a=c>0时，动点M 的轨迹是线段21F F ；（3）当0<a<c 时，动点M 无轨迹。

2．椭圆的标准方程（1）方程的推导：注意根据图形的对称性建立恰当的坐标系，在化简过程中作变化222c a b -=，使方程更为简洁。

（2）两种基本形式：当焦点在x 轴上时，标准方程是)0(12222>>=+b a b y a x ，焦点坐标是)0()0(21，、，c F c F -； 当焦点在y 轴上时，标准方程是)0(12222>>=+b a b x a y ，焦点坐标是)0()0(21c F c F ，、，-。

（3）a 、b 、c 三者的关系：满足222c a b -=即222c b a +=，它们构成了一个直角三角形的三边，其中a 为斜边，b 、c 为直角边（如图1），因而有a>b>0，a>c>0，据此可由方程来确定椭圆的位置。

（4）方程的确定：根据条件确定椭圆标准方程时，常用待定系数法和定义法，首先应确定椭圆的中心和焦点位置，然后根据两个独立条件求出a 、b 的值。

例1（椭圆标准方程的推导）求平面内到点1F （-c,0）, ()2,0F c 的距离和等于2a （0a c >>）的点的轨迹方程。

令222a cb -=，其中0b >， ()222210x y a b a b+=>>例2．根据下列条件，求椭圆的标准方程。

1. 坐标轴为对称轴，并且经过两点A （0，2）和B （12）。

2. 坐标轴为对称轴，一焦点为(，且截直线32y x =-所得弦的中点的横坐标为0.5.3. 经过点（2，-3）且与椭圆229436x y +=有共同的焦点。

高三数学专题练习30 椭圆的定义、标准方程及性质小题基础练○30一、选择题1．椭圆x 24＋y 2＝1的离心率为( ) A.12 B.32C.52 D ．2 答案：B解析：由题意得a ＝2，b ＝1，则c ＝3，所以椭圆的离心率e ＝c a ＝32，故选B.2．[2019·佛山模拟]若椭圆mx 2＋ny 2＝1的离心率为12，则m n ＝( )A.34B.43C.32或233D.34或43 答案：D解析：若焦点在x 轴上，则方程化为x 21m ＋y 21n ＝1，依题意得1m －1n 1m＝14，所以m n ＝34；若焦点在y 轴上，则方程化为y 21n ＋x 21m＝1，同理可得m n ＝43.所以所求值为34或43.故选D.3．过椭圆4x 2＋y 2＝1的一个焦点F 1的直线与椭圆交于A ，B 两点，则A 与B 和椭圆的另一个焦点F 2构成的△ABF 2的周长为( )A ．2B ．4C ．8D ．2 2答案：B解析：因为椭圆方程为4x 2＋y 2＝1，所以a ＝1.根据椭圆的定义，知△ABF 2的周长为|AB |＋|AF 2|＋|BF 2|＝|AF 1|＋|BF 1|＋|AF 2|＋|BF 2|＝(|AF 1|＋|AF 2|)＋(|BF 1|＋|BF 2|)＝4a ＝4.故选B.4．[2018·全国卷Ⅱ]已知F 1，F 2是椭圆C 的两个焦点，P 是C 上的一点．若PF 1⊥PF 2，且∠PF 2F 1＝60°，则C 的离心率为( )A ．1－32 B ．2－ 3C.3－12 D.3－1 答案：D解析：在Rt △PF 1F 2中，∠PF 2F 1＝60°，不妨设椭圆焦点在x 轴上，且焦距|F 1F 2|＝2，则|PF 2|＝1，|PF 1|＝3，由椭圆的定义可知，方程x 2a 2＋y 2b 2＝1中，2a ＝1＋3，2c ＝2，得a ＝1＋32，c ＝1，所以离心率e ＝c a ＝21＋3＝3－1.故选D.5．[2019·河南豫北重点中学联考]已知点P ⎝⎛⎭⎪⎫1，22是椭圆x 2a 2＋y 2＝1(a >1)上的点，A ，B 是椭圆的左、右顶点，则△P AB 的面积为( )A ．2 B.24 C.12 D ．1 答案：D解析：由题可得1a 2＋12＝1，∴a 2＝2，解得a ＝2(负值舍去)，则S △P AB ＝12×2a ×22＝1，故选D.6．[2019·河南安阳模拟]已知F 1，F 2分别是椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，P 为椭圆上一点，且PF 1→·(OF1→＋OP →)＝0(O为坐标原点)．若|PF1→|＝2|PF 2→|，则椭圆的离心率为( ) A.6－ 3 B.6－32C.6－ 5D.6－52 答案：A解析：以OF 1，OP 为邻边作平行四边形，根据向量加法的平行四边形法则，由PF 1→·(OF 1→＋OP →)＝0知此平行四边形的对角线互相垂直，则此平行四边形为菱形，∴|OP |＝|OF 1|，∴△F 1PF 2是直角三角形，即PF 1⊥PF 2.设|PF 2|＝x ，则⎩⎪⎨⎪⎧2x ＋x ＝2a ，(2x )2＋x 2＝(2c )2，∴⎩⎪⎨⎪⎧a ＝2＋12x ，c ＝32x ，∴e ＝c a ＝32＋1＝6－3，故选A.7．若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则OP →·FP→的最大值为( ) A ．2 B ．3C ．6D ．8 答案：C解析：由椭圆x 24＋y 23＝1可得F (－1,0)，点O (0,0)，设P (x ，y )(－2≤x ≤2)，则OP →·FP →＝x 2＋x ＋y 2＝x 2＋x ＋3⎝ ⎛⎭⎪⎫1－x 24＝14x 2＋x＋3＝14(x ＋2)2＋2，－2≤x ≤2，当且仅当x ＝2时，OP →·FP →取得最大值6.故选C.8．[2019·黑龙江大庆模拟]已知直线l ：y ＝kx 与椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)交于A ，B 两点，其中右焦点F 的坐标为(c,0)，且AF 与BF 垂直，则椭圆C 的离心率的取值范围为( )A.⎣⎢⎡⎭⎪⎫22，1B.⎝⎛⎦⎥⎤0，22C.⎝⎛⎭⎪⎫22，1 D.⎝⎛⎭⎪⎫0，22 答案：C解析：由AF 与BF 垂直，运用直角三角形斜边的中线即为斜边的一半，可得|OA |＝|OF |＝c ，由|OA |>b ，即c >b ，可得c 2>b 2＝a 2－c 2，即c 2>12a 2，可得22<e <1.故选C.二、非选择题9．[2019·河南开封模拟]如图，已知圆E ：(x ＋3)2＋y 2＝16，点F (3，0)，P 是圆E 上任意一点．线段PF 的垂直平分线和半径PE 相交于Q .则动点Q 的轨迹Γ的方程为________．答案：x 24＋y 2＝1解析：连接QF ，因为Q 在线段PF 的垂直平分线上，所以|QP |＝|QF |，得|QE |＋|QF |＝|QE |＋|QP |＝|PE |＝4.又|EF |＝23<4，得Q 的轨迹是以E ，F 为焦点，长轴长为4的椭圆即x 24＋y 2＝1.10．[2019·金华模拟]如果方程x 2＋ky 2＝2表示焦点在x 轴上，且焦距为3的椭圆，则椭圆的短轴长为________．答案： 5解析：方程x 2＋ky 2＝2可化为x 22＋y 22k＝1，则⎝ ⎛⎭⎪⎫322＋2k ＝2⇒2k ＝54，∴短轴长为2×52＝ 5.11．[2019·陕西检测]已知P 为椭圆x 2a 2＋y 2b 2＝1(a >b >0)上一点，F 1，F 2是其左、右焦点，∠F 1PF 2取最大值时cos ∠F 1PF 2＝13，则椭圆的离心率为________．答案：33解析：易知∠F 1PF 2取最大值时，点P 为椭圆x 2a 2＋y 2b 2＝1与y轴的交点，由余弦定理及椭圆的定义得2a 2－2a23＝4c 2，即a ＝3c ，所以椭圆的离心率e ＝c a ＝33.12．[2019·“超级全能生”联考]已知椭圆C ：x 28＋y 22＝1与圆M ：x 2＋y 2＋22x ＋2－r 2＝0(0<r <2)，过椭圆C 的上顶点P 作圆M 的两条切线分别与椭圆C 相交于A ，B 两点(不同于P 点)，则直线P A 与直线PB 的斜率之积等于________．答案：1解析：由题可得，圆心为M (－2，0)，P (0，2)．设切线方程为y ＝kx ＋ 2.由点到直线的距离公式得，d ＝|－2k ＋2|1＋k2＝r ，化简得(2－r 2)k 2－4k ＋(2－r 2)＝0，则k 1k 2＝1.课时增分练○30一、选择题 1．[2019·河北省五校联考]以椭圆上一点和两个焦点为顶点的三角形的面积的最大值为1，则椭圆长轴长的最小值为( )A ．1 B. 2 C ．2 D ．2 2 答案：D解析：设a ，b ，c 分别为椭圆的长半轴长、短半轴长、半焦距，依题意知，12×2cb ＝1⇒bc ＝1,2a ＝2b 2＋c 2≥22bc ＝22，当且仅当b ＝c ＝1时，等号成立．故选D.2．[2019·深圳模拟]过点(3,2)且与椭圆3x 2＋8y 2＝24有相同焦点的椭圆方程为( )A.x 25＋y 210＝1B.x 210＋y 215＝1 C.x 215＋y 210＝1 D.x 210＋y 25＝1答案：C解析：椭圆3x 2＋8y 2＝24的焦点为(±5，0)，可得c ＝5，设所求椭圆的方程为x 2a 2＋y 2b 2＝1，可得9a 2＋4b 2＝1，又a 2－b 2＝5，得b 2＝10，a 2＝15，所以所求的椭圆方程为x 215＋y210＝1.故选C.3．一个椭圆的中心在原点，焦点F 1，F 2在x 轴上，P (2，3)是椭圆上一点，且|PF 1|，|F 1F 2|，|PF 2|成等差数列，则椭圆的方程为( )A.x 28＋y 26＝1B.x 216＋y 26＝1 C.x 24＋y 22＝1 D.x 28＋y 24＝1 答案：A解析：设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)．由点P (2，3)在椭圆上知4a 2＋3b 2＝1.又|PF 1|，|F 1F 2|，|PF 2|成等差数列，则|PF 1|＋|PF 2|＝2|F 1F 2|，即2a ＝2×2c ，c a ＝12， 又c 2＝a 2－b 2，联立⎩⎪⎨⎪⎧4a 2＋3b 2＝1，c 2＝a 2－b 2，c a ＝12得a 2＝8，b 2＝6，故椭圆方程为x 28＋y26＝1.故选A.4．[2018·全国卷Ⅱ]已知F 1，F 2是椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，A 是C 的左顶点，点P 在过A 且斜率为36的直线上，△PF 1F 2为等腰三角形，∠F 1F 2P ＝120°，则C 的离心率为( )A.23B.12C.13D.14 答案：D解析：如图，作PB ⊥x 轴于点B .由题意可设|F 1F 2|＝|PF 2|＝2，则c ＝1， 由∠F 1F 2P ＝120°，可得|PB |＝3，|BF 2|＝1， 故|AB |＝a ＋1＋1＝a ＋2，tan ∠P AB ＝|PB ||AB |＝3a ＋2＝36，解得a ＝4，所以e ＝c a ＝14. 故选D. 5．[2019·广西桂林柳州联考]已知点P 是以F 1，F 2为焦点的椭圆x 2a 2＋y 2b 2＝1(a >b >0)上一点．若PF 1⊥PF 2，tan ∠PF 2F 1＝2，则椭圆的离心率e 为( )A.53B.13C.23D.12 答案：A解析：∵点P 是以F 1，F 2为焦点的椭圆x 2a 2＋y 2b 2＝1(a >b >0)上一点，PF 1⊥PF 2，tan ∠PF 2F 1＝2，∴|PF 1||PF 2|＝2.设|PF 2|＝x ，则|PF 1|＝2x ，由椭圆定义知x ＋2x ＝2a ，∴x ＝2a 3，∴|PF 2|＝2a3，则|PF 1|＝4a 3.由勾股定理知|PF 2|2＋|PF 1|2＝|F 1F 2|2，解得c ＝53a ，∴e ＝c a ＝53.故选A.6．已知F 1，F 2是椭圆x 216＋y 29＝1的两焦点，过点F 2的直线交椭圆于A ，B 两点．在△AF 1B 中，若有两边之和是10，则第三边的长度为 ( )A ．6B ．5C ．4D ．3 答案：A解析：根据椭圆定义，知△AF 1B 的周长为4a ＝16，故所求的第三边的长度为16－10＝6.故选A.7．[2019·贵州遵义联考]已知m 是两个数2,8的等比中项，则圆锥曲线x 2＋y2m ＝1的离心率为( )A.32或52B.32或 5C.32 D. 5 答案：B解析：由题意得m 2＝16，解得m ＝4或m ＝－4.当m ＝4时，曲线方程为x 2＋y 24＝1，故其离心率e 1＝c a ＝ 1－b 2a 2＝ 1－14＝32；当m ＝－4时，曲线方程为x 2－y 24＝1，故其离心率e 2＝c a ＝ 1＋b 2a 2＝ 1＋4＝ 5.所以曲线的离心率为32或 5.故选B.8．若椭圆b 2x 2＋a 2y 2＝a 2b 2(a >b >0)和圆x 2＋y 2＝⎝ ⎛⎭⎪⎫b 2＋c 2有四个交点，其中c 为椭圆的半焦距，则椭圆的离心率e 的取值范围为( )A.⎝ ⎛⎭⎪⎫55，35B.⎝⎛⎭⎪⎫0，25C.⎝ ⎛⎭⎪⎫25，35D.⎝ ⎛⎭⎪⎫35，55答案：A解析：由题意可知，椭圆的上、下顶点在圆内，左、右顶点在圆外，则⎩⎨⎧a >b2＋c ，b <b2＋c ，整理得⎩⎪⎨⎪⎧(a －c )2>14(a 2－c 2)，a 2－c 2<2c ，解得55<e <35.故选A.二、非选择题9．[2019·铜川模拟]已知椭圆x 24＋y 23＝1的左焦点为F ，直线x ＝m 与椭圆交于点A 、B ，当△F AB 的周长最大时，△F AB 的面积是________．答案：3 解析：如图，设椭圆的右焦点为E ，连接AE 、BE .由椭圆的定义得，△F AB 的周长为|AB |＋|AF |＋|BF |＝|AB |＋(2a －|AE |)＋(2a －|BE |)＝4a ＋|AB |－|AE |－|BE |.∵|AE |＋|BE |≥|AB |，∴|AB |－|AE |－|BE |≤0，∴|AB |＋|AF |＋|BF |＝4a ＋|AB |－|AE |－|BE |≤4a .当直线AB 过点E 时取等号，此时直线x ＝m ＝c ＝1，把x ＝1代入椭圆x 24＋y 23＝1得y ＝±32，∴|AB |＝3.∴当△F AB 的周长最大时，△F AB的面积是12×3×|EF |＝12×3×2＝3.10．[2019·辽宁沈阳东北育才学校月考]已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)，A ，B 是C 的长轴的两个端点，点M 是C 上的一点，满足∠MAB ＝30°，∠MBA ＝45°.设椭圆C 的离心率为e ，则e 2＝________.答案：1－33 解析：由椭圆的对称性，设M (x 0，y 0)，y 0>0，A (－a,0)，B (a,0)．因为∠MAB ＝30°，∠MBA ＝45°，所以k BM ＝y 0x 0－a ＝－1，k AM ＝y 0x 0＋a＝33.又因为x 20a 2＋y 20b 2＝1，三等式联立消去x 0，y 0可得b 2a 2＝33＝1－e 2，所以e 2＝1－33.11．[2019·云南昆明一中月考]已知中心在原点O ，焦点在x轴上的椭圆E 过点C (0,1)，离心率为22.(1)求椭圆E 的方程；(2)直线l 过椭圆E 的左焦点F ，且与椭圆E 交于A ，B 两点，若△OAB 的面积为23，求直线l 的方程．解析：(1)设椭圆E 的方程为x 2a 2＋y 2b 2＝1(a >b >0)，由已知得⎩⎪⎨⎪⎧b ＝1，c a ＝22，a 2＝b 2＋c 2，解得a 2＝2，b 2＝1，所以椭圆E 的方程为x 22＋y 2＝1.(2)由已知，直线l 过左焦点F (－1,0)．当直线l 与x 轴垂直时，A ⎝ ⎛⎭⎪⎫－1，－22，B ⎝⎛⎭⎪⎫－1，22，此时|AB |＝2，则S △OAB ＝12×2×1＝22，不满足条件． 当直线l 与x 轴不垂直时，设直线l 的方程为y ＝k (x ＋1)，A (x 1，y 2)，B (x 2，y 2)．由⎩⎪⎨⎪⎧y ＝k (x ＋1)，x 22＋y 2＝1得(1＋2k 2)x 2＋4k 2x ＋2k 2－2＝0， 所以x 1＋x 2＝－4k 21＋2k 2，x 1x 2＝2k 2－21＋2k 2.因为S △OAB ＝12|OF |·|y 1－y 2|＝12|y 1－y 2|，由已知S △OAB ＝23得|y 1－y 2|＝43.11因为y 1＋y 2＝k (x 1＋1)＋k (x 2＋1)＝k (x 1＋x 2)＋2k ＝k ·－4k 21＋2k 2＋2k ＝2k 1＋2k 2， y 1y 2＝k (x 1＋1)·k (x 2＋1)＝k 2(x 1x 2＋x 1＋x 2＋1)＝－k 21＋2k 2， 所以|y 1－y 2|＝(y 1＋y 2)2－4y 1y 2＝4k 2(1＋2k 2)2＋4k 21＋2k 2＝43，所以k 4＋k 2－2＝0，解得k ＝±1，所以直线l 的方程为x －y ＋1＝0或x ＋y ＋1＝0.。

椭圆 大题习题及答案解析1已知椭圆()2222:10x y C a b a b +=>>过点()2,0A，且离心率为2．(I)求椭圆C 的方程；(Ⅱ)设直线y kx =+与椭圆C 交于,M N 两点．若直线3x =上存在点P ，使得四边形PAMN 是平行四边形，求k 的值． （（（由题意得 2a =（2c e a ==（ 所以c = 因为 222a b c =+（ 所以 1b =所以 椭圆C 的方程为 2214x y +=（（（（若四边形PAMN 是平行四边形，则 //PA MN ，且 PA MN =. 所以 直线PA 的方程为()2y k x =-，所以 ()3,P k，PA =（设()11,M x y ，()22,N x y （由2244,y kx x y ⎧=+⎪⎨+=⎪⎩ 得()224180k x +++=， 由0∆>，得 212k >（且12241x x k +=-+，122841x x k =+（ 所以MN ==因为 PA MN =， 所以=整理得 421656330k k -+=， 解得k =±，或 k =±经检验均符合0∆>，但2k =-时不满足PAMN 是平行四边形，舍去（所以 k =k =± 2已知椭圆()2222:10x y C a b a b =>>+的左、右焦点分别为12,F F ，124F F =，过2F的直线l 与椭圆C 交于,P Q 两点，1PQF ∆的周长为（1）求椭圆C 的方程；（2）如图，点A ,1F 分别是椭圆C 的左顶点、左焦点，直线m 与椭圆C 交于不同的两点M 、N （M 、N 都在x 轴上方）．且11AF M OF N ∠=∠．证明：直线m 过定点，并求出该定点的坐标.】（1）设椭圆C 的焦距为2c ，由题意，知1224F F c ==，可知2c =，由椭圆的定义知,1PQF ∆的周长为4a =，∴a =24b =∴椭圆C 的方程为22184x y += （2）由题意知，直线的斜率存在且不为0．设直线:l y kx m =+ 设()()1122,,,M x y N x y ，把直线l 代入椭圆方程，整理可得()222124280k x kmx m +++-=,()228840k m ∆=-+>，即22840k m -+>∴122412km x x k +=-+，21222812m x x k -=+，∵111212,22F M F N y y k k x x ==++， ∵M 、N 都x 轴上方．且11AF M OF N ∠=∠，∴11F M F N k k =-，∴121222y y x x =-++，即()()122122y x y x +=-+,代入1122,y kx m y kx m =+=+ 整理可得()()12122240kx x k m x x m ++++=，2121222284,1212m kmx x x x k k -=+=-++ 即222241684840km k k m km k m m ---++=，整理可得4m k =， ∴直线l ()44y kx m kx k k x =+=+=+，∴直线l 过定点()4,0-3已知椭圆C ：22221(0)x y a b a b+=>>的左、右焦点分别为1F 、2F ，点P 、Q 、R分别是椭圆C 的上、右、左顶点，且3PQ PR ⋅=-，点S 是2PF 的中点，且1OS =. （Ⅰ）求椭圆C 的标准方程；（Ⅱ）过点()1,0T -的直线与椭圆C 相交于点M 、N ，若QMN △的面积是125，求直线MN 的方程.解：（Ⅰ）由题意知(),PQ a b =-，(),PR a b =--，∴223PQ PR a b ⋅=-+=-， ∵点S 是2PF 的中点，且1OS =，∴211122OS PF a ===，∴2a =，1b =， 故所求椭圆方程为2214x y +=.（Ⅱ）设()11,M x y ，()22,N x y ，直线MN ：1x ty =-，联立方程组22114x ty x y =-⎧⎪⎨+=⎪⎩，得()224230t y ty +--=， ∴12224t y y t +=+，12234y y t=-+，12y y -==24t =+，∴1211123225QMNS TQ y y =⋅⋅-=⨯=△， ∴1t =±.∴直线MN 的方程为1y x =+或1y x =--.（解法2：求出弦长12N M y =-=点Q 到直线MN 的距离d =11225QMNS MN d ===△， ∴1t =±.∴直线MN 的方程为1y x =+或1y x =--.4如图，椭圆E ：22221(0)x y a b a b+=>>内切于矩形ABCD ，其中AB ，CD 与x 轴平行，直线AC ，BD 的斜率之积为12-，椭圆的焦距为2.（1）求椭圆E 的标准方程；（2）椭圆上的点P ，Q 满足直线OP ，OQ 的斜率之积为12-，其中O 为坐标原点.若M 为线段PQ 的中点，则22MO MQ +是否为定值？如果是，求出该定值；如果不是，说明理由. 【小问1详解】由题意，1c =，则()()()(),,,,,,,A a b B a b C a b D a b ----，所以22AC b bk a a==，22BDb b k a a ==--，所以B AC D k k ⋅=2212b a -=-，解得：a =1=，（椭圆的标准方程为2212x y +=.【小问2详解】（方法一）设()11,P x y ，()22,Q x y ，则1212,22x x y y M ++⎛⎫⎪⎝⎭. 设直线PQ ：y kx t =+，由2212y kx tx y =+⎧⎪⎨+=⎪⎩，得：()222124220k x ktx t +++-=， 12221224122212kt x x k t x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩， 由12OP OQ k k ⋅=-，得()()2212121212212220x x y y k x x kt x x t +=++++=，代入化简得：22212t k =+.（22221212121211222222x x y y x x y y x MO M y Q ++++⎛⎫⎛⎫⎛⎫⎛⎫=++-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭+2222121222x x y y ++=+， 又点P ，Q 在椭圆上，（221112x y +=，222212x y +=，即22221212142x x y y +++=，（()222221212122242222222kt t x x x x x x t t --⎛⎫+=+-=-⋅= ⎪⎝⎭， （2212142x x +=.（2222222212121234242x x y y x x MO MQ ⎛⎫++++=++= ⎪⎝⎭.即2232MO MQ +=为定值. （方法二）由P ，Q 是椭圆C 上的点，可得221122222222x y x y ⎧+=⎨+=⎩， 把12122x x y y =-代入上式，化简22122x y =，得22121y y +=，22122x x +=， ()22221222121322x x y y MO MQ ++==++. 5已知椭圆()2222:10x y C a b a b+=>>的中心是坐标原点O ，左右焦点分别为12,F F ，设P 是椭圆C 上一点，满足2PF x ⊥轴，212PF =，椭圆C的离心率为2（1）求椭圆C 的标准方程；（2）过椭圆C 左焦点1F 且不与x 轴重合的直线l 与椭圆相交于,A B 两点，求2ABF 内切圆半径的最大值.【小问1详解】以2214x y +=．【小问2详解】解：由（1）可知()1F ，222112248ABF CAB AF BF AF BF AF BF a =++=+++==，设直线l为x my =-2214x my x y ⎧=-⎪⎨+=⎪⎩，消去x 得()22410m y +--=，设()11,A x y ，()22,B x y，则1224y y m +=+，12214y y m -=+ 所以1224y y m -===+所以2121212ABF SF F y y =⋅-=，令内切圆的半径为R ，则2182ABF SR =⨯⨯，即24R m =+，令t =，则12t R t==≤=+，当且仅当3t t=，t =，即m =时等号成立，所以当m =R 取得最大值12； 6已知直线220x y 经过椭圆2222:1(0)x y C a b a b+=>>的左顶点A 和上顶点D ，椭圆C 的右顶点为B ，点S 是椭圆C 上位于x 轴上方的动点，直线,AS BS 与直线10:3l x =分别交于,M N 两点．（1）求椭圆C 的方程；（2）求线段MN 的长度的最小值；（3）当线段MN 的长度最小时，在椭圆C 上是否存在这样的点T ，使得TSB △的面积为15，若存在，确定点T 的个数，若不存在，说明理由．【小问1详解】220x y ，令0x =得：1y =，令0y =得：2x =-，所以椭圆C 的左顶点为()2,0A -，上顶点为()0,1D ，所以2,1a b ==，故椭圆方程为2214x y +=.【小问2详解】直线AS 的斜率k 显然存在，且k >0，故可设直线AS 的方程为()2y k x =+，从而1016,33k M ⎛⎫ ⎪⎝⎭，由()22214y k x x y ⎧=+⎪⎨+=⎪⎩，联立得：()222214161640k x k x k +++-=，设()11,S x y ，则212164214k x k --=+，解得：2122814k x k -=+，从而12414k y k =+，即222284,1414k k S k k ⎛⎫- ⎪++⎝⎭，又()2,0B ，由()124103y x k x ⎧=--⎪⎪⎨⎪=⎪⎩，解得：13103y kx ⎧=-⎪⎪⎨⎪=⎪⎩，所以101,33N k ⎛⎫- ⎪⎝⎭，故16133k MN k =+，又0k >，所以1618333k MN k =+≥=，当且仅当16133k k =即14k =时等号成立，故线段MN 的长度的最小值为83.【小问3详解】由第二问得：14k =，此时64,55S ⎛⎫ ⎪⎝⎭，故5SB ==， 要使椭圆C 上存在点T ，使得TSB △的面积等于15，只须T 到直线BS的距离等于24S SB =．其中直线SB ：4056225y x -=--，即20x y +-=，设平行于AB 的直线为0x y t ++=4=解得：32t =-或52t =-，当32t =-时，302x y +-=，联立椭圆方程2214x y +=得：275304y y --=，由9350∆=+>得：302x y +-=与椭圆方程有两个交点；当52t =-时，502x y +-=，联立椭圆方程2214x y +=得：295504y y -+=，由25450∆=-<，此时直线与椭圆方程无交点，综上：点T 的个数为2．满足题意. 所以原题得证，即直线2l 过定点10,03⎛⎫- ⎪⎝⎭7己知椭圆2222:1(0)x y C a b a b+=>>的左､右顶点分别为,A B ，点31,2⎛⎫ ⎪⎝⎭该椭圆上，且该椭圆的右焦点F 与抛物线24y x =的焦点重合. （1）求椭圆C 的标准方程；（2）如图，过点F 且斜率为k 的直线l 与椭圆交于,M N 两点，记直线AM 的斜率为k ，直线BN 的斜率为2k ，直线AN 的斜率3k ，求证：_____________.在以下三个结论中选择一个填在横线处进行证明. （直线AM 与BN 的交点在定直线4x =上；（1213k k =； （1314k k =-..解（因为抛物线24y x =的焦点为(1,0).所以椭圆的右焦点用(1,0)又点31,2⎛⎫ ⎪⎝⎭在该椭圆上，所以221914a b += 又22221a b c b =+=+，所以224,3a b ==椭圆C 的标准方程为22143x y +=（2）选（设()()1122,,,M x y N x y 22(1)143y k x x y =-⎧⎪⎨+=⎪⎩ 联立得：()22223484120k x k x k +-+-=法一：直线11(2),(2)y k x y k x =+=+的交点的横坐标为()12212k k x k k +=-()2121212122212112162442233422481234234k x k k x x x x k x k k k x x x k --+-++==⋅=⋅=--+--+所以直线AM 与BN 的交点在定直线4x =上法二：要证直线AM 与BN 的交点在定直线4x =上，即()122124k k k k +=-，即证1213k k =即证12121232y y x x =+-，即证2212121292y y x x ⎛⎫⎛⎫= ⎪ ⎪+-⎝⎭⎝⎭，即证1212221292x x x x -+=+- 即证()12122580x x x x -++=因为()2212122282482585803434k k x x x x k k ⎛⎫--++=-+= ⎪++⎝⎭所以直线AM 与BN 的交点在定直线4x =上.选（设()()1122,,,M x y N x y ，22(1)143y k x x y =-⎧⎪⎨+=⎪⎩联立得：()22223484120k x k x k +-+-=所以221212228412,3434k k x x x x k k -+==++ 法一：()()()()()()1212112122121212122122222122y x x x k x x x x k x y x x x x x x -----+===++--+- 222112212222221122412846223434134121834128322343434k k k x x x k k k k k k x x x k k k ⎛⎫-----+ ⎪-++⎝⎭+===-⎛⎫---+-- ⎪+++⎝⎭法二：()()12121222y x k k x y -=+ 所以()()()()()()()()222121212121222121212122222422242y x x x x x x x k k x x x x x x x y ----++⎛⎫=== ⎪++++++⎝⎭22222222224121644134344121636943434k k k k k k k k k k--+++===-++++因为12,k k 也同号，所以1213k k =法三：要证1213k k =，即证12121232y y x x =+-，即证2212121292y y x x ⎛⎫⎛⎫= ⎪ ⎪+-⎝⎭⎝⎭即证1212221292x x x x -+=+-，即证()12122580x x x x -++= 因为()2212122282482585803434k k x x x x k k ⎛⎫--++=-+= ⎪++⎝⎭ 所以1213k k =法四：由122(2)143y k x x y =+⎧⎪⎨+=⎪⎩得()2222111341616120k x k x k +++-=得21122116812,3434k k M k k ⎛⎫- ⎪++⎝⎭ 同理22222228612,3434k k N k k ⎛⎫-- ⎪++⎝⎭ 因为,,M N F 为三点共线，所以12221222122212121234346886113434k k k k k k k k -++=----++即()()12214330k k k k +-= 因为12,k k 同号，所以1213k k = 选（设()()1122,,,M x y N x y ，22(1)143y k x x y =-⎧⎪⎨+=⎪⎩联立得：()22223484120k x k x k +-+-=所以221212228412,3434k k x x x x k k -+==++.()()21212121312121212224k x x x x y y k k x x x x x x ⎡⎤-++⎣⎦=⋅=+++++ ()2222222222222222412814128343434141241216121641634434k k k k k k k k k k k k k k k k ⎛⎫--+ ⎪--++++⎝⎭===---+++++++.所以1314k k =-8设椭圆()222210x y a b a b +=>>的离心率为A ，B ，AB 4=．过点(0,1)E ，且斜率为k 的直线l 与x 轴相交于点F ，与椭圆相交于C ，D 两点．（1）求椭圆的方程； （2）若FC DE =，求k 的值；（3）是否存在实数k ，使直线AC 平行于直线BD ？证明你的结论． 【小问1详解】由题意22224b c e a a b c =⎧⎪⎪==⎨⎪-=⎪⎩，解得2a b ⎧=⎪⎨=⎪⎩22164x y +=； 【小问2详解】由题意知，0k ≠，直线l 的方程为1y kx =+，则1(,0)F k -，联立221641x y y kx ⎧+=⎪⎨⎪=+⎩，可得()2223690k x kx ++-=，()223636230k k ∆=++>，设1122(,),(,)C x y D x y ，有12122269,2323k x x x x k k --+==++，则CD 中点横坐标为1223223x x kk+-=+， 又,(0,1),1(0)F k E -，则EF 中点横坐标为12k-，又因为FC DE =，且,,,C E F D 四点共线，取EF 中点H ，则FH HE =，所以H F HE C DE F =--，即HC DH =，所以H 是CD 的中点，即,CD EF 的中点重合，即231232k k k -=-+，解得k = 【小问3详解】不存在实数k ，使直线AC 平行于直线BD ，证明如下：由题意，(0,2),(0,2)A B -，则()()1122,2,,2AC x y BD x y =-=+，若AC BD ，则AC BD ∥，所以()()122122x y x y +=-，即()12211220x y x y x x -++=，即()()()1221121120x kx x kx x x +-+++=， 化简得()121220x x x x -++=，213x x =-，由（2）得，12112266,32323k k x x x x k k --+=-=++，解得12323kx k=+， ()12112299,32323x x x x k k --=⋅-=++解得212323x k =+，所以222332323k k k ⎛⎫= ⎪++⎝⎭，整理得22233k k +=，无解，所以不存实数k ，使直线AC 平行于直线BD .9已知12,F F 分别是椭圆2222:1(0)x y C a b a b+=>>的左、右焦点，过2F 且不与x 轴垂直的动直线l 与椭圆交于,M N 两点，点P 是椭圆C 右准线上一点，连结,PM PN ，当点P 为右准线与x 轴交点时，有2122PF F F =.（1）求椭圆C 的离心率；（2）当点P 的坐标为(2,1)时，求直线PM 与直线PN 的斜率之和. 【详解】解（1）由已知当P 为右准线与x 轴交点时，有2122PF F F =∴222a c c c ⎛⎫-= ⎪⎝⎭∴222c a =∴212e =又(0,1)e ∈，∴2e =. （2）∵(2,1)P ，∴22a c =又222a c =，∴2221a c ⎧=⎨=⎩，∴21b =∴椭圆22:12x C y +=.设直线l ：(1)y k x =-，()()1122,,,M x y N x y联立22(1)22y k x x y =-⎧⎨+=⎩，得()2222124220k x k x k +-+-= 则22121222422,1212k k x x x x k k-+==++， ∴()()121212121111112222PM PN k x k x y y k k x x x x ------++=+----=()()1212212122k x k k x k x x --+--+=+--121211112(1)2222k k k k k k x x x x ⎛⎫--=+++=+-+ ⎪----⎝⎭()()121242(1)22x x k k x x ⎛⎫+-=+- ⎪ ⎪--⎝⎭()12121242(1)24x x k k x x x x ⎛⎫+-=+- ⎪ ⎪-++⎝⎭将22121222422,1212k k x x x x k k-+==++代入得 ()12121242(1)2(1)(2)224PM PN x x k k k k k k x x x x ⎛⎫+-+=+-=+-⨯-= ⎪ ⎪-++⎝⎭.∴直线PM 与直线PN 的斜率之和为2.10已知椭圆22143x y +=，动直线l 与椭圆交于B ，C 两点（B 在第一象限）． （1）若点B 的坐标为31,2⎛⎫ ⎪⎝⎭，求△OBC 面积的最大值；（2）设B （x 1，y 1），C （x 2，y 2），且3y 1+y 2=0，求当△OBC 面积最大时，直线l 的方程． 【小问1详解】 直线OB 的方程为32y x =，即3x -2y =0，设过点C 且平行于OB 的直线l '的方程为32y x b =+， 则当l '与椭圆只有一个公共点时，△OBC 的面积最大．联立221,433,2x y y x b ⎧+=⎪⎪⎨⎪=+⎪⎩消去y 并整理，得3x 2+3bx +b 2-3=0，此时Δ=9b 2-12（b 2-3），令Δ=0，解得b =±当b =C ⎛ ⎝⎭；当b =-时，C ⎭，∴ △OBC=． 【小问2详解】显然可知直线l 与y 轴不垂直，设直线l 的方程为x =my +n ，联立221,43,x y x my n ⎧+=⎪⎨⎪=+⎩消去x 并整理，得（3m 2+4）y 2+6mnx +3n 2-12=0， ∴12221226,34312,34nm y y m n y y m ⎧+=-⎪⎪+⎨-⎪=⎪+⎩∵ 3y 1+y 2=0，∴ 1222123,344,34nm y m n y m ⎧=⎪⎪+⎨-⎪=⎪+⎩ 从而()222222943434n m n m m -=++，即2223431m n m +=+， ∴21212216||6||||2||23431OBCm n m Sn y y n y m m =⋅-=⋅==++． ∵ B 在第一象限，∴ 21123034m nx my n n m =+=+>+，∴ n ＞0．∵ y 1＞0，∴ m ＞0，∴2661313OBCm Sm m m==≤=++当且仅当31m m =，即m =时取等号），此时2n =，∴ 直线l的方程为x y =+，即20y -=．11椭圆2222:1(0)x y C a b a b+=>>的左右焦点为1F ，2F ，过椭圆右焦点2F 的直线l和椭圆C 相交于E 、F 两点，1EFF △的周长为8，若P 是椭圆上一个动点，且12PF PF ⋅的最大值为3． （1）求椭圆C 的方程；（2）四边形MNAB 的四个顶点均在椭圆C 上，且//MB NA ，MB x ⊥轴，若直线MN 和直线AB 交于点()4,0S ，问：四边形MNAB 的对角线交点D 是否是定点？若是，求出定点坐标；若不是，请说明理由． 【详解】（1）解：1EFF △的周长为48a =∴2a =，令222c a b =-设()00,p x y ，1(,0)F c -，2(,0)F c()()20000,,PF PF c x y c x y ⋅=---⋅--2220x c y =-+2222021b x b c a ⎛⎫=-+- ⎪⎝⎭当220x a =时，()22212max3PF PF a c b ⋅=-==∴21c =，∴23b =∴方程为22143x y += （2）解：设 :AM y kx b =+（k 一定存在） 与椭圆联知：()2223484120kxkbx b +++-=设()11,A x y ，()22,M x y ，()11,N x y -，()22,B x y -，122834kb x x k +=-+，212241234b x x k -=+ ，∵M 、N 、S 共线∴2121044y y x x +=-- 得()12122(4)80kx x b k x x b +-+-=，即()222412824803434b kb k b k b k k--⋅+-⋅-=++， 整理可得0k b +=∴:(1)AM y k x =-过点()1,0Q 下证：BN 也过()1,0Q 212111BQ NQ y y k k x x -=---()()()()()()2112211111011k x x k x x x x ----=--=-∴BN 和AM 相交于()1,0()1,0即为定点D .。

椭圆标准方程典型例题例1已知P 点在以坐标轴为对称轴的椭圆上，点P 到两焦点的距离分别为354和352，过P 点作焦点所在轴的垂线，它恰好过椭圆的一个焦点，求椭圆方程． 解：设两焦点为1F 、2F ，且3541=PF ，3522=PF ．从椭圆定义知52221=+=PF PF a ．即5=a ．从21PF PF >知2PF 垂直焦点所在的对称轴，所以在12F PF Rt ∆中，21sin 1221==∠PF PF F PF ，可求出621π=∠F PF ，3526cos21=⋅=πPF c ，从而310222=-=c a b ．∴所求椭圆方程为1103522=+y x 或1510322=+y x ．例2 已知椭圆方程()012222>>=+b a b y a x ，长轴端点为1A ，2A ，焦点为1F ，2F ，P 是椭圆上一点，θ=∠21PA A ，α=∠21PF F ．求：21PF F ∆的面积（用a 、b 、α表示）．分析：求面积要结合余弦定理及定义求角α的两邻边，从而利用C ab S sin 21=∆求面积．解：如图，设()y x P ，，由椭圆的对称性，不妨设()y x P ，，由椭圆的对称性，不妨设P 在第一象限．由余弦定理知：221F F 2221PF PF +=12PF -·224cos c PF =α．①由椭圆定义知： a PF PF 221=+ ②，则－①②2得αcos 12221+=⋅b PF PF ． 故αsin 212121PF PF S PF F ⋅=∆ ααsin cos 12212+=b2tan 2αb =．例3 已知动圆P 过定点()03，-A ，且在定圆()64322=+-y x B ：的内部与其相内切，求动圆圆心P 的轨迹方程．分析：关键是根据题意，列出点P 满足的关系式．解：如图所示，设动圆P 和定圆B 内切于点M ．动点P 到两定点，即定点()03，-A 和定圆圆心()03，B 距离之和恰好等于定圆半径， 即8==+=+BM PB PM PB PA ．∴点P 的轨迹是以A ，B 为两焦点，半长轴为4，半短轴长为73422=-=b 的椭圆的方程：171622=+y x ．说明：本题是先根据椭圆的定义，判定轨迹是椭圆，然后根据椭圆的标准方程，求轨迹的方程．这是求轨迹方程的一种重要思想方法．例4 已知椭圆1222=+y x ，（1）求过点⎪⎭⎫ ⎝⎛2121，P 且被P 平分的弦所在直线的方程；（2）求斜率为2的平行弦的中点轨迹方程；（3）过()12，A 引椭圆的割线，求截得的弦的中点的轨迹方程； （4）椭圆上有两点P 、Q ，O 为原点，且有直线OP 、OQ 斜率满足21-=⋅OQ OP k k ，求线段PQ 中点M 的轨迹方程．分析：此题中四问都跟弦中点有关，因此可考虑设弦端坐标的方法．解：设弦两端点分别为()11y x M ，，()22y x N ，，线段MN 的中点()y x R ，，则⎪⎪⎩⎪⎪⎨⎧=+=+=+=+④，③，②，①，y y y x x x y x y x 222222212122222121①－②得()()()()022*******=-++-+y y y y x x x x ．由题意知21x x ≠，则上式两端同除以21x x -，有()()0221212121=-+++x x y y y y x x ，将③④代入得022121=--+x x y y yx ．⑤（1）将21=x ，21=y 代入⑤，得212121-=--x x y y ，故所求直线方程为： 0342=-+y x ． ⑥ 将⑥代入椭圆方程2222=+y x 得041662=--y y ，0416436>⨯⨯-=∆符合题意，0342=-+y x 为所求．（2）将22121=--x x y y 代入⑤得所求轨迹方程为： 04=+y x ．（椭圆内部分） （3）将212121--=--x y x x y y 代入⑤得所求轨迹方程为： 022222=--+y x y x ．（椭圆内部分）（4）由①＋②得 ： ()2222212221=+++y y x x ， ⑦，将③④平方并整理得212222124x x x x x -=+， ⑧， 212222124y y y y y -=+， ⑨将⑧⑨代入⑦得：()224424212212=-+-y y y x x x ， ⑩再将212121x x y y -=代入⑩式得： 221242212212=⎪⎭⎫ ⎝⎛--+-x x y x x x ， 即 12122=+y x ．此即为所求轨迹方程．当然，此题除了设弦端坐标的方法，还可用其它方法解决．例5 已知椭圆1422=+y x 及直线m x y +=． （1）当m 为何值时，直线与椭圆有公共点？（2）若直线被椭圆截得的弦长为5102，求直线的方程．解：（1）把直线方程m x y +=代入椭圆方程1422=+y x 得()1422=++m x x ， 即012522=-++m mx x ．()()020*********≥+-=-⨯⨯-=∆m m m ，解得2525≤≤-m ．（2）设直线与椭圆的两个交点的横坐标为1x ，2x ，由（1）得5221mx x -=+，51221-=m x x ． 根据弦长公式得 ：51025145211222=-⨯-⎪⎭⎫⎝⎛-⋅+m m ．解得0=m ．方程为x y =．说明：处理有关直线与椭圆的位置关系问题及有关弦长问题，采用的方法与处理直线和圆的有所区别．这里解决直线与椭圆的交点问题，一般考虑判别式∆；解决弦长问题，一般应用弦长公式． 用弦长公式，若能合理运用韦达定理（即根与系数的关系），可大大简化运算过程．例6 以椭圆131222=+y x 的焦点为焦点，过直线09=+-y x l ：上一点M 作椭圆，要使所作椭圆的长轴最短，点M 应在何处？并求出此时的椭圆方程．解：如图所示，椭圆131222=+y x 的焦点为()031，-F ，()032，F ． 点1F 关于直线09=+-y x l ：的对称点F 的坐标为（－9，6），直线2FF 的方程为032=-+y x ．解方程组⎩⎨⎧=+-=-+09032y x y x 得交点M 的坐标为（－5，4）．此时21MF MF +最小．所求椭圆的长轴：562221==+=FF MF MF a ，∴53=a ，又3=c ，∴()3635322222=-=-=c a b ．因此，所求椭圆的方程为1364522=+y x ．例7 求中心在原点，对称轴为坐标轴，且经过)2,3(-A 和)1,32(-B 两点的椭圆方程．解：设所求椭圆方程为122=+ny mx (0>m ，0>n )．由)2,3(-A 和)1,32(-B 两点在椭圆上可得 ⎪⎩⎪⎨⎧=⋅+-⋅=-⋅+⋅,11)32(,1)2()3(2222n m n m 即⎩⎨⎧=+=+,112,143n m n m 所以151=m ，51=n ．故所求的椭圆方程为151522=+y x ．例8 已知长轴为12，短轴长为6，焦点在x 轴上的椭圆，过它对的左焦点1F 作倾斜解为3π的直线交椭圆于A ，B 两点，求弦AB 的长．分析：可以利用弦长公式]4))[(1(1212212212x x x x k x x k AB -++=-+=求得，也可以利用椭圆定义及余弦定理，还可以利用焦点半径来求． 解：(法1)利用直线与椭圆相交的弦长公式求解．2121x x k AB -+=]4))[(1(212212x x x x k -++=．因为6=a ，3=b ，所以33=c ．因为焦点在x 轴上，所以椭圆方程为193622=+y x ，左焦点)0,33(-F ，从而直线方程为93+=x y ．由直线方程与椭圆方程联立得：0836372132=⨯++x x ．设1x ，2x 为方程两根，所以1337221-=+x x ，1383621⨯=x x ，3=k ， 从而1348]4))[(1(1212212212=-++=-+=x x x x k x x k AB(法2)利用椭圆的定义及余弦定理求解．由题意可知椭圆方程为193622=+y x ，设m AF =1，n BF =1，则m AF -=122，n BF -=122．在21F AF ∆中，3cos22112212122πF F AF F F AF AF -+=，即21362336)12(22⋅⋅⋅-⋅+=-m m m ；所以346-=m ．同理在21F BF ∆中，用余弦定理得346+=n ，所以1348=+=n m AB ．(法3)利用焦半径求解．先根据直线与椭圆联立的方程0836372132=⨯++x x 求出方程的两根1x ，2x ，它们分别是A ，B 的横坐标．再根据焦半径11ex a AF +=，21ex a BF +=，从而求出11BF AF AB +=．例9 椭圆192522=+y x 上的点M 到焦点1F 的距离为2，N 为1MF 的中点，则ON （O 为坐标原点）的值为A ．4B ．2C ．8D ．23说明：(1)椭圆定义：平面内与两定点的距离之和等于常数（大于21F F ）的点的轨迹叫做椭圆．(2)椭圆上的点必定适合椭圆的这一定义，即aMF MF 221=+，利用这个等式可以解决椭圆上的点与焦点的有关距离例10 已知椭圆13422=+y x C ：，试确定m 的取值范围，使得对于直线m x y l +=4：，椭圆C 上有不同的两点关于该直线对称．解：设椭圆上),(11y x A ，),(22y x B 两点关于直线l 对称，直线AB 与l 交于),(00y x M 点．∵l 的斜率4=l k ，∴设直线AB 的方程为n x y +-=41．由方程组⎪⎪⎩⎪⎪⎨⎧=++-=,134,4122y x n x y 消去y 得0481681322=-+-n nx x ①。

椭圆方程练习题一、选择题1. 下列方程中，表示椭圆的是（）A. x^2 + y^2 = 1B. x^2 + 4y^2 = 4C. 2x^2 + 3y^2 = 6D. x^2 y^2 = 12. 椭圆的标准方程中，a和b的关系是（）A. a > bB. a < bC. a = bD. 无法确定3. 椭圆的离心率e满足（）A. 0 < e < 1B. e = 1C. e > 1D. e = 04. 下列关于椭圆的说法，正确的是（）A. 长轴和短轴都在x轴上B. 长轴和短轴都在y轴上C. 长轴和短轴互相垂直D. 长轴和短轴的长度相等二、填空题1. 椭圆的标准方程为 $\frac{x^2}{a^2} + \frac{y^2}{b^2} =1$，其中a为椭圆的______，b为椭圆的______。

2. 椭圆的离心率e定义为 $e = \frac{c}{a}$，其中c为椭圆的______。

3. 若椭圆的焦点在x轴上，则椭圆的方程为 $\frac{x^2}{a^2}+ \frac{y^2}{b^2} = 1$，其中a > b，若椭圆的焦点在y轴上，则椭圆的方程为______。

4. 椭圆的面积S为______。

三、解答题1. 已知椭圆的焦点坐标为F1(4, 0)和F2(4, 0)，且经过点P(0, 3)，求椭圆的标准方程。

2. 椭圆的一个焦点在原点，另一个焦点在x轴上，且离心率为0.5，已知椭圆经过点(4, 0)，求椭圆的标准方程。

3. 已知椭圆的方程为 $\frac{x^2}{25} + \frac{y^2}{16} = 1$，求椭圆的焦点坐标、离心率和面积。

4. 设椭圆的方程为 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$，若椭圆的离心率为 $\frac{1}{2}$，求a和b的关系。

5. 已知椭圆的焦点在x轴上，且离心率为$\frac{\sqrt{3}}{2}$，椭圆经过点(0, 2)，求椭圆的标准方程。