模拟退火算法讲义(数学建模)
- 格式:pdf
- 大小:703.83 KB
- 文档页数:35

中国数学建模-编程交流-模拟退火算法模拟退火算法模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
根据Metropolis准则,粒子在温度T 时趋于平衡的概率为e-ΔE/(kT),其中E为温度T时的内能,ΔE为其改变量,k为Boltzmann 常数。
用固体退火模拟组合优化问题,将内能E模拟为目标函数值f,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法:由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。
退火过程由冷却进度表(CoolingSchedule)控制,包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。
3.5.1 模拟退火算法的模型模拟退火算法可以分解为解空间、目标函数和初始解三部分。
模拟退火的基本思想:(1) 初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点),每个T值的迭代次数L(2) 对k=1,……,L做第(3)至第6步:(3) 产生新解S′(4) 计算增量Δt′=C(S′)-C(S),其中C(S)为评价函数(5) 若Δt′<0则接受S′作为新的当前解,否则以概率exp(-Δt′/T)接受S′作为新的当前解.(6) 如果满足终止条件则输出当前解作为最优解,结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少,且T->0,然后转第2步。
算法对应动态演示图:模拟退火算法新解的产生和接受可分为如下四个步骤:第一步是由一个产生函数从当前解产生一个位于解空间的新解;为便于后续的计算和接受,减少算法耗时,通常选择由当前新解经过简单地变换即可产生新解的方法,如对构成新解的全部或部分元素进行置换、互换等,注意到产生新解的变换方法决定了当前新解的邻域结构,因而对冷却进度表的选取有一定的影响。


数学建模模拟退火算法
数学建模是一种将实际问题转化为数学问题,通过建立数学模型来分析和解决问题的方法。
而模拟退火算法则是一种基于概率的全局优化算法,常被用于求解复杂问题的最优解。
在数学建模中,模拟退火算法可以应用于各种领域,如图像处理、目标识别、路线规划等。
模拟退火算法的基本思想是从一个随机解开始,通过随机扰动和接受策略来探索可能解空间,并逐渐降温,使得随机扰动的程度逐渐减小,最终达到全局最优解。
在应用模拟退火算法时,需要确定初始温度、温度下降速度以及接受策略等参数。
在数学建模中,模拟退火算法可以应用于很多问题。
例如,在图像处理中,可以通过模拟退火算法对图像进行优化,如图像的平滑处理、边缘检测等。
在目标识别领域,模拟退火算法可以用于对目标进行跟踪和识别。
在路线规划问题中,模拟退火算法可以用于求解最优路径。
在应用模拟退火算法时,需要考虑算法的效率和精度。
为了提高效率,可以采用多种优化技巧,如快速随机数生成、启发式信息引导等。
为了提高精度,可以适当增加迭代次数和初始温度,以便探索更广泛的解空间。
总之,模拟退火算法是一种非常有用的全局优化算法,可以应用于很多数学建模问题中。
在实际应用中,需要根据具体问题的特点和需求来选择算法参数和优化技巧,以达到最佳效果。
- 1 -。
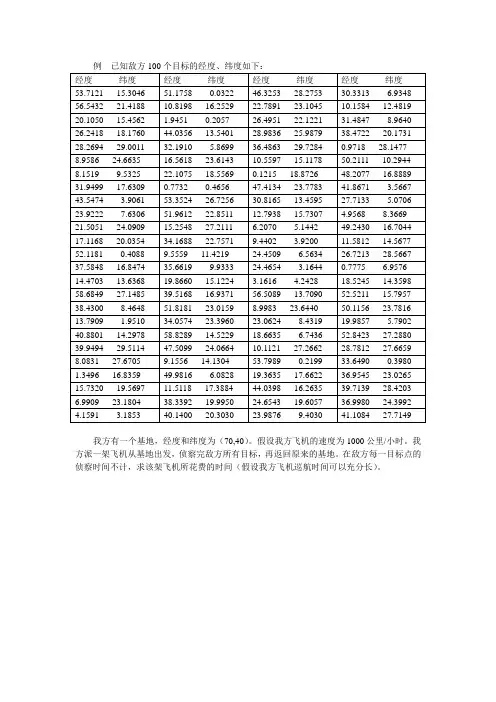
例已知敌方100个目标的经度、纬度如下:我方有一个基地,经度和纬度为(70,40)。
假设我方飞机的速度为1000公里/小时。
我方派一架飞机从基地出发,侦察完敌方所有目标,再返回原来的基地。
在敌方每一目标点的侦察时间不计,求该架飞机所花费的时间(假设我方飞机巡航时间可以充分长)。
这是一个旅行商问题。
我们依次给基地编号为1,敌方目标依次编号为2,3,…,101,最后我方基地再重复编号为102(这样便于程序中计算)。
距离矩阵102102)(⨯=ij d D ,其中ij d 表示表示j i ,两点的距离,102,,2,1, =j i ,这里D 为实对称矩阵。
则问题是求一个从点1出发,走遍所有中间点,到达点102的一个最短路径。
上面问题中给定的是地理坐标(经度和纬度),我们必须求两点间的实际距离。
设B A ,两点的地理坐标分别为),(11y x ,),(22y x ,过B A ,两点的大圆的劣弧长即为两点的实际距离。
以地心为坐标原点O ,以赤道平面为XOY 平面,以0度经线圈所在的平面为XOZ 平面建立三维直角坐标系。
则B A ,两点的直角坐标分别为:)s i n ,c o s s i n ,c o s c o s(11111y R y x R y x R A )s i n ,c o s s i n ,c o s c o s(22222y R y x R y x R B 其中6370=R 为地球半径。
B A ,两点的实际距离⎫⎛=R d arccos , 化简得]s i n s i n c o s c o s )(a r c c o s [co s 212121y y y y x x R d +-=。
求解的模拟退火算法描述如下:(1)解空间解空间S 可表为{102,101,,2,1 }的所有固定起点和终点的循环排列集合,即}102,}101,,3,2{),,(,1|),,{(102101211021===ππππππ的循环排列为 S其中每一个循环排列表示侦察100个目标的一个回路,j i =π表示在第i 次侦察j 点,初始解可选为)102,,2,1( ,本文中我们使用Monte Carlo 方法求得一个较好的初始解。







模拟退火算法讲义1.基本思想2.算法流程(1)初始化初始解,设为当前解;(2)设置初温T和下降速度参数α;(3)在当前温度下进行随机邻域,寻找更好的解;(4)每次得到新解后,计算其目标函数值与当前解的目标函数值之差ΔE;(5)若ΔE小于等于0,或满足一定的概率条件P(ΔE,T),则接受新解作为当前解;(6)降低温度,即T=T*α;(7)若满足停止条件,则算法终止,否则回到步骤(3);(8)输出当前解作为最优解。
3.关键问题(1)初始温度的选择:初始温度过高可能导致无法跳出局部最优解,而初始温度过低可能导致无法找到全局最优解。
一种常用的方法是通过多次试验来确定初始温度,使其能够在相对较短的时间内找到一个较优解。
(2)温度下降速度的选择:温度下降速度决定了算法的收敛速度,过快的下降速度会导致陷入局部最优解,而过慢的下降速度则会使算法收敛速度过慢。
通常可以通过实验来确定一个适合的下降速度参数α。
(3)邻域算子的选择:邻域算子是指在当前解的邻域内进行,从而寻找更好的解。
常见的邻域算子有随机扰动法、交换相邻解法等。
具体选择哪种算子需要根据具体问题的特点来确定。
4.算法优缺点(1)算法具有较好的全局能力,能够跳出局部最优解,具有一定的随机性;(2)算法易于实现,并且没有太多的问题依赖,适用于各种类型的问题;(3)由于算法采用随机策略,所以有一定的概率陷入局部最优解,需要调节参数来平衡全局和局部的能力。
总结起来,模拟退火算法是一种基于随机的启发式算法,通过温度的不断降低来达到在解空间中全局最优解的目的。
虽然算法具有较好的全局能力,但在实际应用中还需要根据具体问题的特点来选择合适的参数和邻域算子,以取得较好的效果。
数学建模模拟退火算法数学建模是一项重要的研究方法,在各个学科领域都有广泛应用。
而退火算法是一种常见的优化算法,它通过模拟物质的退火过程来寻找问题的最优解。
下面本文将为大家介绍数学建模模拟退火算法的步骤。
首先,数学建模的第一步是选择问题及建立模型。
在这里,我们以旅行商问题为例进行讲解。
旅行商问题是指一个旅行商要走遍n个城市,并回到起点,问他应该按照怎样的顺序走才能使路程最短。
构建旅行商问题的数学模型,需要确定城市的坐标、距离矩阵等相关数据。
其次,建立目标函数,描述问题的优化目标。
在旅行商问题中,我们的目标是使路程最短。
因此,目标函数可以表示成:$${ \min \sum_{i,j=1}^{n} d_{i,j} x_{i}x_{j}}$$ 其中,dij表示城市i和城市j之间的距离,xi和xj则代表城市i 和城市j是否构成了回路。
接下来,我们需要确定退火算法的参数。
其中包括:初始温度T,降温速度a,迭代次数N和状态转移概率函数p。
其中,初始温度设置越高,容错率将越高;降温速度越慢,计算时间越长;迭代次数越多,则搜索的区域将越大;状态转移概率函数可以采用“metropolis准则”,即:$$ p=\begin{cases} 1\quad \Delta f\le 0 \\ e^{-\Delta f/T}\quad \Delta f>0 \end{cases} $$ 其中,△f代表目标函数的变化量,T表示当前温度,e为自然常数,越小则接受非最优解的概率也就越小。
最后,进行模拟退火算法的求解过程。
具体步骤包括:初始化,生成初始解;计算目标函数;降温,进行状态转移;重复上述过程,去掉个别的极值,直到收敛。
综上所述,数学建模模拟退火算法是一种有效的优化算法,和其他算法相比,模拟退火算法不需要求目标函数的导数,适用于非线性、非凸优化问题。
同时,该算法分类简单,容易实现,因此在实际应用中得到了广泛的推广和应用。
第二章模拟退火算法(Simulated Annealing)搜索问题描述搜索问题描述搜索算法盲目搜索还是启发式搜索?按照预定的控制策略实行搜索,在搜索过程中获取的中间信息不用来改进控制策略,称为盲目搜索,反之,称为启发式搜索。
关于“启发式”,可有两种看法:1)任何有助于找到问题的解,但不能保证找到解的方法均是启发式方法;2)有助于加速求解过程和找到较优解的方法是启发式方法。
搜索算法盲目搜索深度优先、广度优先、代价优先、向前、向后、双向。
启发式搜索爬山法、模拟退火算法、遗传算法、粒子群算法、蚁群算法。
贪心算法1.随机选定一个初始解x 0;2.Do while (中止条件不满足)1.在某个邻域函数所定义的邻域范围内,按照某个(随机)扰动Δ产生策略,得到一个新解x i ’;2.对新解进行评估,得f (x i ’);3.如果f (x i ’) > f (x i )(或者f (x i ’) < f (x i )),即新解比老解好,则令x i +1=x i ’;4.否则,x i +1=x i 。
3.End Do爬山法1.随机选定一个初始解x 0;2.Do while (中止条件不满足)1.在某个邻域函数所定义的邻域范围内,按照某个(随机)扰动Δ产生策略,得到多个新解X new ={x i 1, x i2,…, x i k };2.对这组新解进行评估,得{f (x i 1), f (x i 2), …, f (x i k )};3.x i +1=x i ’,x i ’∈X new ,∀x i j , (i =1,2,…,n; j =1,2,…,k ), f (x i ’) > f (x i )且f(x i ’) > f (x i j )(或者f (x i ’) < f (x i )且f (x i ’) < f (x i j )),即新的当前解比老解好,并且是所有新解中最好的一个;4.如果,∀x i j , (i =1,2,…,n; j =1,2,…,k ), f(x i ) > f (x i j )(或者f (x i ) <f (x i j )),则x i +1=x i 。
第二章模拟退火算法(Simulated Annealing)
搜索问题描述
搜索问题描述
搜索算法
盲目搜索还是启发式搜索?
按照预定的控制策略实行搜索,在搜索过程中获取的中间信息不用来改进控制策略,称为盲目搜索,反之,称为启发式搜索。
关于“启发式”,可有两种看法:
1)任何有助于找到问题的解,但不能保证找到解的
方法均是启发式方法;
2)有助于加速求解过程和找到较优解的方法是启发
式方法。
搜索算法
盲目搜索
深度优先、广度优先、代价优先、向前、向后、双
向。
启发式搜索
爬山法、模拟退火算法、遗传算法、粒子群算法、
蚁群算法。
贪心算法
1.
随机选定一个初始解x 0;2.Do while (中止条件不满足)
1.
在某个邻域函数所定义的邻域范围内,按照某个(随机)扰动Δ产生策略,得到一个新解x i ’;2.
对新解进行评估,得f (x i ’);3.
如果f (x i ’) > f (x i )(或者f (x i ’) < f (x i )),即新解比老解好,则令x i +1=x i ’;4.否则,x i +1=x i 。
3.End Do
爬山法
1.
随机选定一个初始解x 0;2.Do while (中止条件不满足)
1.
在某个邻域函数所定义的邻域范围内,按照某个(随机)扰动Δ产生策略,得到多个新解X new ={x i 1, x i2,…, x i k };2.
对这组新解进行评估,得{f (x i 1), f (x i 2), …, f (x i k )};3.
x i +1=x i ’,x i ’∈X new ,∀x i j , (i =1,2,…,n; j =1,2,…,k ), f (x i ’) > f (x i )且f(x i ’) > f (x i j )(或者f (x i ’) < f (x i )且f (x i ’) < f (x i j )),即新的当前解比老解好,并且是所有新解中最好的一个;4.如果,∀x i j , (i =1,2,…,n; j =1,2,…,k ), f(x i ) > f (x i j )(或者f (x i ) <
f (x i j )),则x i +1=x i 。
3.End Do
特点
特点
遇到平台则无以事从
算法设计要素
编码策略(“个体表示”与“问题解”的映射关系) 初始解的产生(从什么位置开始搜索)
邻域函数的设计(下一个解的产生概率与当前解之间距离[包括方向和步长]的关系)
新解产生策略(随机,确定)
接受策略(贪心)
存在问题:
对初始解(状态)敏感 容易陷入局部最优
模拟退火算法(起源)
物理退火原理
Real annealing:
Sword
He heats the metal, then slowly cools it as he hammers the blade into
shape.
If he cools the blade too
quickly the metal will form
patches of different
composition;
If the metal is cooled slowly
while it is shaped, the
constituent metals will form
a uniform alloy.
模拟退火算法(起源)
物理退火过程:
加温过程
等温过程
冷却(退火)过程
等温下热平衡过程可用Monte Carlo方法模拟,计算量大。
1953年,Metropolis提出重要性采样法,即以概率接受新状态,称Metropolis准则,计算量相对Monte Carlo方法显著减少。
1983年,Kirkpatrick等提出模拟退火算法,并将其应用于组合优化问题的求解。
则)
模拟退火算法与物理退火过程的相似关系
模拟退火算法(流程)
1)随机产生一个初始解x 0,令x best =x 0,并计算目标函数值E (x 0);
2)设置初始温度T (0)=T o ,迭代次数i = 1;
3)Do while T (i )> T min
1)for j = 1~k
2)对当前最优解x best 按照某一邻域函数,产生一新的解x new 。
计算新的目
标函数值E (x new ),并计算目标函数值的增量ΔE = E (x new )-E (x best )。
3)如果ΔE <0,则x best = x new ;
4)如果ΔE >0,则p = exp(-ΔE /T (i ));
1)如果c = random[0,1] < p ,x best = x new ; 否则x best = x best 。
5)End for
4)i = i +1;
5)End Do
6)输出当前最优点,计算结束。
模拟退火算法(要素)
1、状态空间与状态产生函数(邻域函数)
搜索空间也称为状态空间,它由经过编码的可行解的集合所组成。
状态产生函数(邻域函数)应尽可能保证产生的候选解遍布全部解空间。
通常由两部分组成,即产生候选解的方式和候选解产生的概率分布。
候选解一般采用按照某一概率密度函数对解空间进行随机采样来获得。
概率分布可以是均匀分布、正态分布、指数分布等等。
模拟退火算法(要素)
模拟退火算法(要素)
模拟退火算法(要素)
4、初始温度T 0
实验表明,初温越大,获得高质量解的几率越大,但花费的计算时间将增加。
因此,初温的确定应折衷考虑优化质量和优化效率,常用方法包括:
(1) 均匀抽样一组状态,以各状态目标值的方差为初温。
(2) 随机产生一组状态,确定两两状态间的最大目标值差|Δmax |,然后依据差值,利用一定的函数确定初温。
比如,t 0=-Δmax /p r ,其中p r 为初始接受概率。
(3) 利用经验公式给出。
模拟退火算法(要素)
5、内循环终止准则
或称Metropolis抽样稳定准则,用于决定在各温度下产生候选解的数目。
常用的抽样稳定准则包
括:
(1) 检验目标函数的均值是否稳定;
(2) 连续若干步的目标值变化较小;
(3) 按一定的步数抽样。
模拟退火算法(要素)
6、外循环终止准则
即算法终止准则,常用的包括:
(1) 设置终止温度的阈值;
(2) 设置外循环迭代次数;
(3) 算法搜索到的最优值连续若干步保持不变;
(4) 检验系统熵是否稳定。
模拟退火算法的改进
(1) 设计合适的状态产生函数,使其根据搜索进程的需要
表现出状态的全空间分散性或局部区域性。
(2) 设计高效的退火策略。
(3) 避免状态的迂回搜索。
(4) 采用并行搜索结构。
(5) 为避免陷入局部极小,改进对温度的控制方式
(6) 选择合适的初始状态。
(7) 设计合适的算法终止准则。
模拟退火算法的改进
也可通过增加某些环节而实现对模拟退火算法的改进。
主要的改进方式包括:
(1) 增加升温或重升温过程。
在算法进程的适当时机,将温度适当提
高,从而可激活各状态的接受概率,以调整搜索进程中的当前状态,避免算法在局部极小解处停滞不前。
(2) 增加记忆功能。
为避免搜索过程中由于执行概率接受环节而遗失
当前遇到的最优解,可通过增加存储环节,将“Best So Far”的状态记忆下来。
(3) 增加补充搜索过程。
即在退火过程结束后,以搜索到的最优解为
初始状态,再次执行模拟退火过程或局部性搜索。
(4) 对每一当前状态,采用多次搜索策略,以概率接受区域内的最优
状态,而非标准SA的单次比较方式。
(5) 结合其他搜索机制的算法,如遗传算法、混沌搜索等。
(6)上述各方法的综合应用。
算法实现与应用
结果(400个城市)
结果(400个城市)。