升余弦滚降系统设计

实验一升余弦滚降系统及眼图、实验目的1. 理解无码间串扰系统的原理；2. 理解升余弦滚降系统的工作原理;3. 理解眼图的工作原理及实现方法。

、实验仪器及软件电脑、MATLAB7.0软件三、实验原理1. 无码间串扰系统若想消除码间串扰，应有a n h k n T s t00 （1-1）n k由于a n是随机的，要想通过各项相互抵消使码间串扰为0是不行的，这就需要对h t的波形提出要求，如果相邻码元的前一个码元的波形到达后一个码元抽样判决时刻时已经衰减到0,如图1-1（a）所示的波形，就能满足要求。

但这样的波形不易实现，因为实际中的h t波形有很长的“拖尾”，也正是由于每个码元拖尾"造成对相邻码元的串扰，但只要让它在t0 T s，t0 2T s等后面码元抽样判决时刻上正好为0，就能消除码间串扰，如图1-1（b）所示。

这也是消除码间串扰的基本思想。

著名的奈奎斯特第一准则就给出了无码间串扰时基带传输特性应满足的频率条件：(1-2)图1-1消除码间串扰显然，满足式（1-2）的系统H 并不是唯一的，容易想到的一种就是H 为一个理想低通滤波器。

2. 升余弦滚降系统理想低通特性的基带系统具有最大的频带利用率。

但实际上理想低通系统在应用中存在两个问题： 是实现极为困难，二是理想的冲击响应h t 的“拖尾”很长，衰减很慢，当定时存在偏差时，可能出现严重的码间串扰。

实际使用中常采用升余弦频谱特性的系统，其系统传输特性如下:T s ,0其中， 称为滚降系数。

其单位冲激响应为sin t T s cos g 一tT s yl 43. 眼图一个实际的基带传输系统尽管经过了十分精心的设计，但要 使其传输特性完全符合理想情况是非常困难的，甚至是不可能的。

码间干扰问题与发送滤波器特性、信道特性、接收滤波器特性等 因素有关，因而计算由于这些因素所引起的误码率就非常困难， 尤其在信道特性不能完全确知的情况下，甚至得不到一种合适的 定量分析方法。

通信原理软件实验报告学院：信息与通信工程学院班级：一、通信原理Matlab仿真实验实验八一、实验内容假设基带信号为m(t)=sin(2000*pi*t)+2cos(1000*pi*t),载波频率为20kHz，请仿真出AM、DSB-SC、SSB信号，观察已调信号的波形和频谱。

二、实验原理1、具有离散大载波的双边带幅度调制信号AM该幅度调制是由DSB-SC AM信号加上离散的大载波分量得到，其表达式及时间波形图为：应当注意的是，m(t)的绝对值必须小于等于1，否则会出现下图的过调制：AM信号的频谱特性如下图所示：由图可以发现，AM信号的频谱是双边带抑制载波调幅信号的频谱加上离散的大载波分量。

2、双边带抑制载波调幅（DSB—SC AM）信号的产生双边带抑制载波调幅信号s(t)是利用均值为0的模拟基带信号m(t)和正弦载波c(t)相乘得到，如图所示：m(t)和正弦载波s(t)的信号波形如图所示：若调制信号m(t)是确定的，其相应的傅立叶频谱为M(f)，载波信号c(t)的傅立叶频谱是C(f),调制信号s(t)的傅立叶频谱S(f)由M(f)和C(f)相卷积得到，因此经过调制之后，基带信号的频谱被搬移到了载频fc处，若模拟基带信号带宽为W，则调制信号带宽为2W，并且频谱中不含有离散的载频分量，只是由于模拟基带信号的频谱成分中不含离散的直流分量。

3、单边带条幅SSB信号双边带抑制载波调幅信号要求信道带宽B=2W, 其中W是模拟基带信号带宽。

从信息论关点开看，此双边带是有剩余度的，因而只要利用双边带中的任一边带来传输，仍能在接收机解调出原基带信号，这样可减少传送已调信号的信道带宽。

单边带条幅SSB AM信号的其表达式：或其频谱图为：三、仿真设计1、流程图：Array2、实验结果&分析讨论实验仿真结果从上至下依次是AM信号、DSB信号、SSB信号。

从仿真结果看，AM调制信号包络清晰，可利用包络检波恢复原信号，接收设备较为简单。

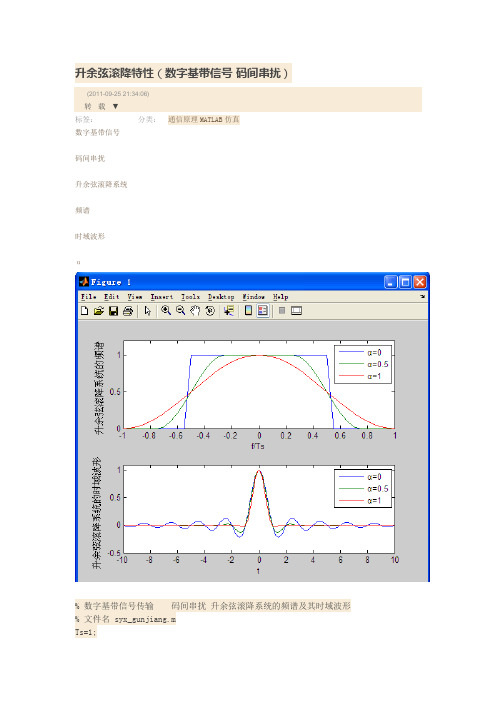
升余弦滚降特性（数字基带信号码间串扰）(2011-09-25 21:34:06)转载▼标签：分类：通信原理MATLAB仿真数字基带信号码间串扰升余弦滚降系统频谱时域波形α% 数字基带信号传输码间串扰升余弦滚降系统的频谱及其时域波形% 文件名 syx_gunjiang.mTs=1;N=17;dt=Ts/N;df=1.0/(20.0*Ts);t=-10*Ts:dt:10*Ts;f=-2/Ts:df:2/Ts;a=[0,0.5,1];for n=1:length(a)for k=1:length(f)if abs(f(k))>0.5*(1+a(n))/TsXf(n,k)=0;elseif abs(f(k))<0.5*(1-a(n))/TsXf(n,k)=Ts;elseXf(n,k)=0.5*Ts*(1+cos(pi*Ts/(a(n)+eps)*(abs(f(k))-0.5*( 1-a(n))/Ts)));end;end;xt(n,:)=sinc(t/Ts).*(cos(a(n)*pi*t/Ts))./(1-4*a(n)^2*t.^2/Ts^2+eps); endsubplot(211);plot(f,Xf);axis([-1 1 0 1.2]);xlabel('f/Ts');ylabel('升余弦滚降系统的频谱');legend('α=0','α=0.5','α=1');subplot(212);plot(t,xt);axis([-10 10 -0.5 1.1]);xlabel('t');ylabel('升余弦滚降系统的时域波形');legend('α=0','α=0.5','α=1');赵鸿图茅艳主编通信原理MATLAB仿真教程[M]. 人民邮电出版社 p213。

太原理工大学现代科技学院现代通信原理课程实验报告专业班级通信17-3 学号 2017101086 姓名丁一帆指导教师李化实验名称 2ASK 调制与解调Matlab Simulink 仿真 同组人专业班级 通信17-3 学号 2017101086 姓名 丁一帆 成绩一、实验目的1．掌握 2ASK 的调制原理和 Matlab Simulink 仿真方法 2．掌握 2ASK 的解调原理和 Matlab Simulink 仿真方法 二、实验原理2ASK 二进制振幅调制就是用二进制数字基带信号控制正弦载波的幅度，使载波振幅随着二进制数字基带信号而变化，而其频率和初始相位保持不变。

信息比特是通过载波的幅度来传递的。

其信号表达式为：0()()cos c e t S t t ω=⋅，S(t)为单极性数字基带信号。

由于调制信号只有0或1两个电平，相乘的结果相当于将载频或者关断，或者接通，它的实际意义是当调制的数字信号“1”时，传输载波；当调制的数字信号为“0”时，不传输载波。

2ASK 信号的时间波形e2ASK(t)随二进制基带信号S(t)通断变化。

所以又被称为通断键控信号 三、实验内容、步骤1 Simulink 模型的建立通过Simulink 的工作模块建立2ASK 二级调制系统，用频谱分析仪观察调制前后的频谱，用示波器观察调制信号前后的波形……………………………………装………………………………………订…………………………………………线………………………………………正弦波源，这里使用的是Signal Processing Blockset\DSP Sources\Sine Wave，设定其幅度为2V，频率为2Hz。

基带信号源，使用的是Communications Blockset\Comm Sources\Random Data Sources\Bernoulli Binary Generator，可以产生随机数字波形。

升余弦滚降滤波器的作用升余弦滚降滤波器（Raised Cosine Rolloff Filter）是一种常用的数字通信系统中的滤波器。

它的作用是用于调整信号的带宽，以减小信号的带外泄漏，并且在频域上具有平滑的过渡特性。

升余弦滚降滤波器通常用于调制和解调过程中，特别是在正交幅度调制（QAM）和正交频分多路复用（OFDM）系统中，以提高系统的性能和抗干扰能力。

在数字通信系统中，信号经过调制传输到信道中，会受到各种噪声和干扰的影响，导致信号的失真和误差。

升余弦滚降滤波器可以对信号进行预处理，使其在通过传输信道之前具有更好的性能。

具体来说，升余弦滚降滤波器可以起到以下几个方面的作用：1. 带宽控制：升余弦滚降滤波器可以调整信号的带宽，限制信号的频谱分布在所需的范围内。

通过控制滤波器的参数，可以实现信号的带宽压缩或展宽，以适应不同的传输需求。

2. 频谱形状控制：升余弦滚降滤波器在频域上具有平滑的过渡特性，可以减小信号在过渡频段上的幅度变化。

这样可以有效地减小信号的带外泄漏，降低对其他信号的干扰。

3. 抗多径干扰：在无线通信系统中，信号会经过多条路径传播到接收端，导致多径干扰。

升余弦滚降滤波器可以通过控制滤波器的时域特性，使信号在时域上具有较长的冲激响应，从而减小多径干扰的影响。

4. 时频特性匹配：在正交调制和解调过程中，升余弦滚降滤波器可以用于匹配发送端和接收端的时频特性。

通过在发送端和接收端都使用相同的滤波器，可以保持信号的相干性，提高系统的传输效率和可靠性。

升余弦滚降滤波器在数字通信系统中具有广泛的应用。

在正交幅度调制（QAM）系统中，升余弦滚降滤波器常用于发送端对数字信号进行调制，以及接收端对接收到的信号进行解调。

在正交频分多路复用（OFDM）系统中，升余弦滚降滤波器用于子载波的生成和接收端的信号处理。

此外，升余弦滚降滤波器还可以应用于其他数字通信系统中，如调幅、调频和调相等。

总结起来，升余弦滚降滤波器在数字通信系统中起到了带宽控制、频谱形状控制、抗多径干扰和时频特性匹配等作用。

实验 升余弦滚降系统设计一、实验目的1．掌握升余弦滚降系统工作原理；2．掌握模升余弦滚降系统的Matlab 建模方法； 3．掌握模升余弦滚降系统的Matlab 仿真方法。

二、实验仪器1．PC 机一台 2．Matlab 软件一套三、实验原理升余弦函数T t TTTstttt g sss22241)cos()sin()(ααπππ-⋅=，对应的频谱为⎪⎪⎪⎩⎪⎪⎪⎨⎧+>+≤<---+-≤≤=TTTT T T Tssss s s sf f f f Ts f G 222221||01||1))1|(|cos(1(21||0)(ααααααπ四：实验结果五、实验总结当α=1时候，眼图睁开最大，峰值失真最小。

但由图可见它的主瓣最宽，频带利用率最低， 这是它所付出的代价。

当α=0.05时候,频带利用率高，但眼图最不明显，码间干扰最大，同时对抽样时间定时要求特别严格，这使得他在物理上比较难实现。

当α=0.5时候，虽然两个性能都不是最优，但综合两因素，它还是不错，因此实际中，常采用此系统。

为此，后面的实验考虑到直观性，没有考虑带宽限制，均取α＝1。

六、代码设计考虑到α的变化，本实验对应产生一个m ×N 的矩阵保存所有α对应码元信号，同时使用了矩阵参数的fft 函数，由于它是安列分别进行变化的，故用列保存对应一个α的码元的。

tic %开始计时global dt t df Nclose allN=2^15; %采样点数L=32; %每码元的采样点数M=N/L; %码元数Rb=2; %码速率是2Mb/sW=Rb/2;Ts=1/Rb; %码元间隔dt=Ts/L; %时域采样间隔df=1/(N*dt); %频域采样间隔T=N*dt; %截短时间Bs=N*df/2; %系统带宽Na=4; %示波器扫描宽度为4个码元Again=10;alpha=[0.05,0.5,1]'; %alpha变化参数，可方便修改：）Nalpha=length(alpha);t=[-T/2+dt/2:dt:T/2]; %时域横坐标f=[-Bs+df/2:df:Bs]; %频域横坐标tempalpha=ones(Nalpha,1); %tempalpha＝[1,1,1]，所以tempalpha*t为3*1向量与1*N向量＝3×N向量，g1=sin(tempalpha*pi*t/Ts)./(tempalpha*pi*t/Ts);%g2=cos(alpha*pi*t/Ts)./(1-(2*alpha*t/Ts).^2);g= g1.*g2 ; %升余弦脉冲波形g=g'; %用N*3矩阵按列保存一种alpha对应的gG= fft(g) ; %fft(3*N矩阵)将按列进行fft变换G=[G(N/2+1:N,:);G(1:N/2,:)]*dt;SumP=zeros(length(f),Nalpha)+eps;for jj=1:Again%产生冲击序列a=sign(randn(M,Nalpha))+1; %值0,2imp=zeros(N,Nalpha); %生冲激序列figure(3)for indexalpha=1:Nalphaimp(L/2:L:N,indexalpha)=a(:,indexalpha)/dt;subplot(Nalpha,1,indexalpha);title(['\alpha=',num2str(alpha(indexalpha)),'时的眼图']);hold onend %得到接收端输出信号，同时观察眼图%由于imp是N*3的数组，故不能直接调用t2fH=fft(imp);H=[H(N/2+1:N,:);H(1:N/2,:)]*dt;S= H.*G ; %升余弦信号的傅氏变换SumP=SumP+S.*conj(S)/T;S=[S(N/2+1:N,:);S(1:N/2,:)];s=real(ifft(S)/dt); %得到接收端输出信号tt=[0:dt:Na*L*dt];if jj==1 %为加快运行速度，只观察一次眼图figure(3)for jj=1:Na*L:N-Na*Lfor indexalpha=1:Nalphasubplot(Nalpha,1,indexalpha);plot(tt,s(jj:jj+Na*L,indexalpha));hold onendendendendP=SumP/Again;for ii=1:Nalpha%画不同alpha时的时域g(t)与频域G(f)figure(1);subplot(3,2,2*ii-1)plot(t/Ts,g(:,ii)); %用Ts对时间归一化axis([-5,5,-0.5,1.2]); %截取归一化时间轴title(['\alpha=',num2str(alpha(ii)), '时的g(t)-t/Ts'],'fontsize',15);ylabel('g(t)','fontsize',17)subplot(3,2,2*ii)plot(2*f/Rb,Rb*abs(G(:,ii)));axis([-5,5,-0.5,1.2]);ylabel('G(f)','fontsize',17)title(['\alpha=',num2str(alpha(ii)), '时的频普'],'fontsize',15); %画不同alpha时的功率普figure(2);subplot(3,1,ii)plot(2*f/Rb,30+10*log10(P(:,ii)*2*W));axis([-5,5,-50,100]);ylabel('P(f)','fontsize',17)title(['\alpha=',num2str(alpha(ii)), '时的功率普'],'fontsize',15); endusetime= toc。

第五章 数字信号的基带传输基带传输系统频带传输系统（调制传输系统）数字基带信号：没有经过调制的原始数字信号。

（如各种二进制码PCM 码，M ∆码等）数字调制信号：数字基带信号对载波进行调制形成的带通信号。

5.1、基带信号的码型一、数字基带信号的码型设计原则：1． 对传输频带低端受限的信道，线路传输的码型的频谱中应该不含有直流分量；2．信号的抗噪声能力强；3．便于从信号中提取位定时信息；4．尽量减少基带信号频谱中的高频分量，节省传输频带、减小串扰； 5．编译码设备应尽量简单。

二、数字基带信号的常用码型。

1、单极性不归零码NRZ （Non Return Zero ）脉冲宽度τ等于码元宽度T特点：（1）有直流，零频附近的低频分量一般信道难传输。

（2）收端判决门限与信号功率有关，不方便。

（3）要求传输线一端接地。

（4）不能用滤波法直接提取位定时信号。

2、双极性非归零码（BNRZ ）T =τ，有正负电平特点：不能用滤波直接提取位定时信号。

⎩⎨⎧数字通信系统3、单极性归零码（RZ）τ<T特点：（1）可用滤波法提取位同步信号（2）NRZ的缺点都存在4、双极性归零码（BRZ）特点：（1）整流后可用滤波提取位同步信号（2）NRZ的缺点都不存在5、差分码电平跳变表1，电平不变表0 称传号差分码电平跳变表0，电平不变表1 称空号差分码特点：反映相邻代码的码元变化。

6、传号交替反转码（AMI）τ）归零码表0用零电平表示，1交替地用+1和-1半占空（T5.0=示。

优点：（1）“0”、“1”不等概时也无直流（2）零频附近低频分量小（3）整流后即为RZ码。

缺点：连0码多时，AMI整流后的RZ码连零也多，不利于提取高质量的位同步信号（位同频道抖动大）应用：μ律一、二、三次群接口码型：AMI加随机化。

7、三阶高密度双极性码()3HDBHDB3码编码步骤如下。

①取代变换：将信码中4个连0码用取代节000V或B00V代替，当两个相邻的V码中间有奇数个1码时用000V代替4个连0码，有偶数个1码时用B00V代替4个连0码。

移动通信设计题目：C语言实现升余弦滚降信号的匹配接收班级：08通信B姓名：谭洋学号：0815232015指导老师：陈东华一、 设计原理余弦特性滚降的传输函数可表示为相应的h(t)为式中，α为滚降系数，用于描述滚降程度。

它定义为 其中，fN － 奈奎斯特带宽，f ∆ － 超出奈奎斯特带宽的扩展量当α=1时，即为升余弦频谱特性，这时H(ω)可表示为其单位冲激响应为：二、实现程序程序如下：#include <math.h>#include <stdio.h>#define pi 3.141592653589793/* 本函数实现滚降特性函数,升余弦滤波器说明:fs/fd 必须为整数,fd 为信号采样频率,fs 为滤波器采样频率 当函数返回0时为正常返回,为-1时为异常返回*/int rcosine(float fd,float fs,float rcs[]) /* 函数(升余弦滤波器)返回0为正常返回,-1为异常返回 */{int k,n;float kf,nf;nf=fs/fd; n=int(nf);if(nf!=n) return(-1); /* 当fs/fd 不是整数时异常返回 */ for(k=0; k<3*n; k++)⎪⎪⎪⎩⎪⎪⎪⎨⎧+≥+<≤--+-<≤=S S S S S S S S T T T T T T T T H παωπαωπαωπαπαωω)1(,0)1()1()],(2sin 1[2)1(0,)(()222sin /cos //14/S S S S t T t T h t t T t T παππα=⋅-/Nf f α∆=⎪⎪⎩⎪⎪⎨⎧>≤+=s s s s T T T T H πωπωωω2,02),2cos 1(2)(2241cos sin )(s s s s T t T t T t T t t h -∙=πππ{ kf=k-3*n;if(kf==-n) rcs[k]=0;else{ nf=kf/n; kf=pi*nf;rcs[k]=(sin(kf)/kf)*(cos(kf/2)/(1-nf*nf));}rcs[6*n-k]=rcs[k];}rcs[3*n]=1.0;return(0); /* 当fs/fd是整数时正常返回 */ }void main( ){ int flag,i;static float rcs[200];flag=rcosine(0.6,12.0,rcs);if(flag==0)for(i=0;i<200;i++)printf("%.4f\t",rcs[i]);else printf("\n\n error!");scanf("%d",&i);}三、测试结果程序运行结果如下图：由上图可看出程序运行结果即为升余弦滚降特性曲线的离散点。

第六章仿真作业
余弦滚降系统
用matlab 画出α=0,0.5,1的余弦滚降系统的频谱，并画出各自对应的时域波形。

以
α=1的余弦滚降系统为例，进行二进制双极性数字基带信号传输，试画出接收端
的基带信号波形及眼图。

1. 余弦滚降系统频谱图
如图，频域波形在滚降段中心频率处呈奇对称特性，满足奈奎斯特第一准则。

图可证明，滚降系数越大，超出奈奎斯特带宽的扩展量越大，要求带宽增大。

2. 余弦滚降系统时域波形
如图，滚降系数越大，波形的拖尾衰减越快，对位定时精度要求越低。

f/Ts
H (f )
t
h (t )
3. 接收端的基带信号波形
如图，波形幅度没有衰减，无码间串扰。

可通过抽样判决后还原接收信号。

4. 接收端的基带信眼图
若干段数字基带波形叠加后形成眼图形状。

眼图“眼睛”张开越大，眼图越端正，表示码间串扰越小。

上图为理想状态下的眼图，不存在码间串扰。

20
2530
354045
t/Ts
基带信号
0123
45678
-1.5
-1
-0.5
0.5
1.5
t/Ts
e y e。