特定要素模型
- 格式:doc
- 大小:351.00 KB
- 文档页数:21


特定要素模型是一种经济学理论,用于分析资源配置和国际贸易的影响。
根据特定要素模型,一个国家的资源配备情况决定了该国在国际贸易中的优势和劣势,从而影响了贸易模式和经济发展。
特定要素模型的结论可以总结如下:
1. 资源分工:根据特定要素模型,资源在不同国家之间的分工将导致贸易的发展。
资源丰富的国家倾向于出口使用该资源的产品,而缺乏该资源的国家则从其他国家进口。
2. 比较优势:根据特定要素模型,一个国家在某种特定要素(如劳动力、土地或资本)拥有相对较多的资源,将在该要素相关产业中具有比较优势。
这意味着,这个国家将倾向于专注于生产和出口该产业的产品。
3. 收入分配:特定要素模型认为,国际贸易的存在会对国内的收入分配产生影响。
资源拥有者(如劳动者或资本家)在自己资源所具有的比较优势产业中将受益,并相对更富裕。
然而,其他资源的相对劣势产业可能会导致资源拥有者受到竞争压力。
4. 福利效应:特定要素模型认为,国际贸易能够增加参与国的整体福利水平。
通过利用自己的比较优势,国家能够获得更多的生产效率和消费选择,从而提高总体福利。
需要注意的是,特定要素模型过于简化了实际情况,忽略了许多现实中的复杂性。
因此,在使用特定要素模型进行分析时,需要结合实际情况和其他经济模型进行综合考量。




特定要素模型是保罗·萨缪尔森和罗纳德·琼斯创建发展的,主要用于解释短期内,国际贸易对收入分配的影响。
这个模型假定一个国家生产两种产品,劳动供给可以在两个部门间进行配置。
与李嘉图模型不同的是,特定要素模型中存在劳动以外的生产要素,劳动可以在部门间流动,是一种流动要素。
其他要素则是特定的,只能被用与生产某些特定产品。
所谓特定要素,是指一种要素的用途通常仅限于某一部门,而不适合于其他部门的需要。
如汽车行业的资本不能用于纺织行业,纺织行业的资本也不适合于汽车行业,因此,这两个行业所使用的都是特定资本。
在短期内,假设有一个生产要素是固定不变的,即不能加以调整,而另一个生产要素则可自由变动。
通常我们视资本在短期内是不能变动的,即在不同部门间不能自由流动。
之所以认为资本在短期内不能流动,一个主要理由是资本在短期内属于一种“特定要素”(Specific factor)。
关于生产要素性质的分析也同样适用于另外一种情形:生产要素包括三种,但每种生产只使用其中的两种要素。
例如,小麦生产使用土地和劳动两种要素,而服装生产使用资本和劳动。
实际上,在这个例子中,土地和资本都属于特定要素,只不过这里要素的特定性与时间无关,所以以下的特定要素模型同样适用于分析三种要素下的特定要素问题。
根据特定的要素模型所的出的结论是:贸易对一国流动要素的影响是不明确的,同时将有利于用于该国出口商品的非流动要素,而不利于该国进口商品的非流动要素。
特定要素模型的基本假设[1]特定要素模型的基本结构,与前面的要素禀赋理论相比,除了关于要素流动性的假设不同外,其他方面基本相同。
其具体包括:∙X、Y两种产品生产都使用资本和劳动;∙规模收益不变;∙劳动是同质的,可在两个部门间自由流动;∙劳动总量是固定的,并且充分就业;∙资本是特定生产要素,即两个部门的资本不能互相使用;∙每个部门的资本投入都是固定不变的;∙所有商品市场和要素市场都是完全竞争的。


特定要素模型特定要素模型是由保尔·萨缪尔森和罗纳德·琼斯创建发展的。
像简单的李嘉图模型一样,特定要素模型假定一个国家生产两种产品,劳动供给可以在两个部门间进行配置。
与李嘉图模型不同的是,特定根本模型中存在劳动以外的生产要素。
劳动可以在部门间流动,是一种流动要素。
其他要素则是特定的,它们只能被用于生产某些特定产品。
一、模型的假设设想一个国家能够生产两种产品——制造品和粮食。
这个国家有三种生产要素:劳动(L) 、资本(K) 和土地(T) 。
生产制造品需要投入劳动和资本,不需要土地。
生产粮食需要投入劳动和土地,不需要资本。
因此劳动是一种流动要素,每个部门都需要使用劳动。
同时,土地和资本都是特定要素,各自只用于一种产品的生产。
如何确定每种产品的产量呢? 制造品的产出取决于在制造业部门中投入的资本和劳动的多少。
产出和投入之间的关系可以用生产函数来归纳。
生产函数表明在劳动和资本的投人量一定时制造品的产出量。
制造品的生产函数的代数形式为:Q M =Q M (K ,L M )式中,Q M 表示制造品的产出,K 表示资本存量,L M 表示在制造品生产中投入的劳动。
同样地,粮食的生产函数可以表示为:Q F =Q F (T ,L F )式中,Q F 表示粮食的产出,T 表示土地的供给量,L F 表示在粮食生产中投入的劳动。
从国家整体上来说,各部门投入的劳动之和等于总的劳动供给量L :L M +L F =L二、生产可能性特定要素模型假设每一种特定要素只能被用于一个生产部门:资本只能用来生产制造品,土地只能用来生产粮食,只有劳动可以用于各部门的生产。
因此,要分析一国的生产可能性,我们只需知道当劳动从一个部门转移到另一个部门时,制造品和粮食的产出组合是怎样变化的。
这个问题可能用画图的方法解决。
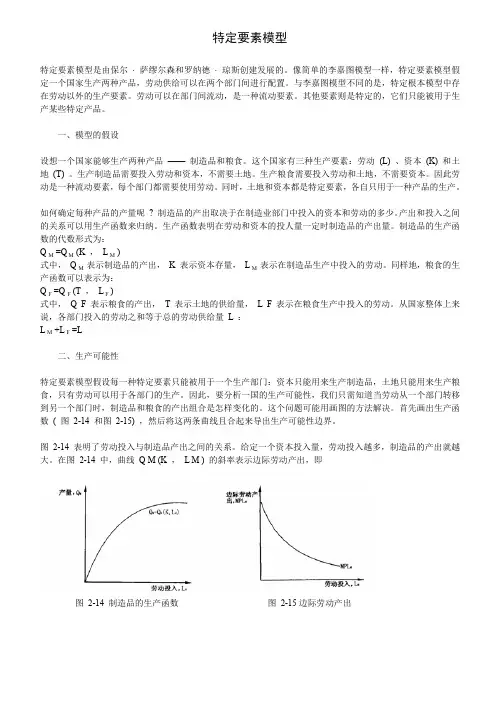
首先画出生产函数( 图2-14 和图2-15) ,然后将这两条曲线且合起来导出生产可能性边界。
图2-14 表明了劳动投入与制造品产出之间的关系。

特定要素模型范文特定要素模型,也被称为特定要素分析模型,是一种由美国军方开发的分析工具,用于帮助决策者或管理者更好地理解问题,并制定相应的解决方案。
特定要素模型的核心思想是将问题分解成一系列关键因素,并分析它们之间的相互关系,以便更好地进行决策。
首先,确定问题是特定要素模型的第一步。
在这一步骤中,决策者或管理者需要明确问题的本质和目标,以便能够明确分析和解决。
接下来,决策者或管理者需要确定问题的要素。
要素是指影响问题的因素,可以是内部因素,如资源,技术和人力等,也可以是外部因素,如政治,经济和环境等。
通过识别关键要素,决策者或管理者可以更好地理解问题,并为制定解决方案提供指导。
在确定问题的要素后,分析这些要素之间的关系是特定要素模型的另一个重要步骤。
通过分析要素之间的相互关系,可以了解不同要素之间的相互影响和依赖关系。
这有助于决策者或管理者确切确定问题的根本原因,并帮助他们制定解决方案。
最后一步是制定解决方案。
通过了解问题的要素和它们之间的关系,决策者或管理者可以制定相应的解决方案。
在制定解决方案时,决策者或管理者需要考虑各个要素的重要性,并找到一种平衡的解决方案。
特定要素模型的优势在于它能够帮助决策者或管理者更全面地理解问题,并从整体上进行分析和解决。
它提供了一个结构化的方法,将决策过程分解成一系列关键因素,以便更好地理解它们之间的相互关系。
这有助于决策者或管理者做出更明智的决策,并采取合适的行动。
然而,特定要素模型也有一些限制。
首先,它假设影响问题的要素和它们之间的关系是静态的。
然而,实际上,这些要素和关系可能会随着时间的推移而变化。
其次,特定要素模型并不能提供具体的数据和解决方案,而只是为决策者或管理者提供了一种分析问题的方法。
总之,特定要素模型是一种管理工具,通过分析问题的关键要素之间的关系,帮助决策者或管理者更好地理解问题,并制定解决方案。
它提供了一个结构化的方法,使决策过程更加系统化和完整。

国际贸易特定要素模型国际贸易特定要素模型(Heckscher-Ohlin模型)是经济学中用来解释国际贸易的一个重要理论模型,该模型主要关注生产要素的差异对国际贸易的影响。
特定要素模型最早由瑞典经济学家Eli Heckscher和Bertil Ohlin提出,他们认为国际贸易取决于各国生产要素的差异。
其中,生产要素主要包括劳动力、资本和技术等。
这些生产要素的差异决定了各国在不同产品上的生产能力和成本水平。
特定要素模型的核心思想是,一个国家拥有相对丰富的生产要素将会在这个要素的使用上处于优势地位。
举个例子来说,如果一个国家拥有大量廉价劳动力,那么它在劳动密集型产业(如纺织业)的生产上将会更具竞争力。
相反,如果一个国家拥有大量资本,那么它在资本密集型产业(如汽车制造业)的生产上将会更具竞争力。
特定要素模型的基本假设是完全竞争市场和均衡贸易模式。
在一个完全竞争市场中,生产要素的价格由市场供求决定,而均衡贸易模式则指的是国际贸易当中,各国的生产要素价格将最终趋于均衡。
在特定要素模型中,国际贸易的主要动力是不同国家生产要素的差异。
在一个两个国家的世界中,每个国家都会专注于利用其相对丰富的生产要素进行生产。
一个国家会专注于生产使用其相对丰富因素的商品,并通过出口这些商品来获取收入。
相对贫乏该要素的国家则会从别国进口该要素丰富的商品。
这种专业化和互相依赖的贸易关系将会带来相互的利益。
特定要素模型的另一个重要结论是资源再分配的效应。
当一个国家开始专注于生产其相对丰富的要素的商品时,这将导致该要素的需求增加,价格上涨。
相反,相对缺乏该要素的国家将会面临该要素的供给过剩,价格下降。
这种资源再分配的效应将会导致在全球范围内生产要素价格的趋同。
特定要素模型也提供了关于收入分配的一些有趣观点。
根据该模型,相对有利于生产该要素的国家将会在该要素价格上升时从中受益。
而相对缺乏该要素的国家将会在该要素价格下降时从中受益。
因此,特定要素模型强调了贸易对于不同国家、不同社会阶层的收入影响。
特定要素模型的基本内容特定要素模型的基本内容特定要素模型是经济学中的一个重要概念,它描述了在一个开放的经济系统中,特定要素(如劳动力、资本等)的供给和需求如何决定其价格和配置。
本文将介绍特定要素模型的基本内容,包括特定要素的定义和特性、识别和分类、在生产过程中的作用和地位、供给和需求分析、市场的结构和运作机制、价格决定及变化趋势以及政策和管理等方面。
一、特定要素的定义和特性特定要素是指一个经济系统中对生产某种产品或服务必不可少的资源或要素,如劳动力、资本、土地等。
这些要素具有以下特性:1. 不可替代性:特定要素在生产过程中不可替代,离开了它们,生产无法进行。
2. 稀缺性:特定要素的数量有限,不足以满足所有生产需求。
3. 需求多样性:不同产品或服务需要不同的特定要素组合和配置。
二、特定要素的识别和分类在特定要素模型中,识别和分类特定要素是非常重要的。
根据不同的标准,可以将特定要素分为不同的类型。
例如,根据要素在生产中的作用,可以分为直接要素和间接要素;根据要素的流动性,可以分为可贸易要素和不可贸易要素。
这些分类有助于我们更好地理解和分析特定要素市场的运作。
三、特定要素在生产过程中的作用和地位在生产过程中,特定要素扮演着重要的角色。
它们直接参与生产活动,对产品的质量和数量有着决定性的影响。
特定要素的地位取决于它们在生产中的重要性和稀缺程度。
在一些产业中,如高科技产业,资本和知识密集型要素占据主导地位;而在一些传统产业中,劳动力和自然资源等要素则更为重要。
四、特定要素的供给和需求分析特定要素的供给和需求分析是特定要素模型的核心内容之一。
供给方面,由于特定要素的稀缺性,供给曲线通常向右上方倾斜。
需求方面,产品或服务的市场需求决定了对特定要素的需求,进而形成要素的需求曲线。
特定要素的需求曲线通常向右下方倾斜,表明随着产品或服务价格的上升,对特定要素的需求会减少。
五、特定要素市场的结构和运作机制特定要素市场的结构通常受到市场规模、市场分割、信息不对称等因素的影响。
特定要素模型名词解释
特定要素模型是一种用于描述系统或组织中不同元素之间关系
的模型。
这些要素可以是人员、流程、技术或其他资源。
这个模型的目的是提高系统或组织的效率和效果,并帮助管理者做出更准确的决策。
在特定要素模型中,每个要素都被定义为一个单独的实体,并与其他要素之间的联系相连接。
这些连接可以是实体之间的物理联系,也可以是抽象的概念联系。
特定要素模型通常包括以下几个要素:
1. 人员:这些要素通常与组织的员工和领导层相关。
2. 流程:这些要素描述了系统或组织中的不同流程和活动。
3. 技术:这些要素通常与系统或组织中使用的技术和工具相关。
4. 资源:这些要素描述了系统或组织中可用的实际资源,例如资金、设备和物资等。
特定要素模型的应用场景非常广泛,包括业务流程重组、系统设计、项目管理和团队协作等。
它可以帮助管理者更好地了解组织内部的各个要素之间的关系,从而更好地管理和优化资源的使用,提高工作效率和效果。
- 1 -。
特定要素模型特定要素模型是由保尔·萨缪尔森和罗纳德·琼斯创建发展的。
像简单的李嘉图模型一样,特定要素模型假定一个国家生产两种产品,劳动供给可以在两个部门间进行配置。
与李嘉图模型不同的是,特定根本模型中存在劳动以外的生产要素。
劳动可以在部门间流动,是一种流动要素。
其他要素则是特定的,它们只能被用于生产某些特定产品。
一、模型的假设设想一个国家能够生产两种产品——制造品和粮食。
这个国家有三种生产要素:劳动(L) 、资本(K) 和土地(T) 。
生产制造品需要投入劳动和资本,不需要土地。
生产粮食需要投入劳动和土地,不需要资本。
因此劳动是一种流动要素,每个部门都需要使用劳动。
同时,土地和资本都是特定要素,各自只用于一种产品的生产。
如何确定每种产品的产量呢? 制造品的产出取决于在制造业部门中投入的资本和劳动的多少。
产出和投入之间的关系可以用生产函数来归纳。
生产函数表明在劳动和资本的投人量一定时制造品的产出量。
制造品的生产函数的代数形式为:Q M =Q M (K ,L M )式中,Q M 表示制造品的产出,K 表示资本存量,L M 表示在制造品生产中投入的劳动。
同样地,粮食的生产函数可以表示为:Q F =Q F (T ,L F )式中,Q F 表示粮食的产出,T 表示土地的供给量,L F 表示在粮食生产中投入的劳动。
从国家整体上来说,各部门投入的劳动之和等于总的劳动供给量L :L M +L F =L二、生产可能性特定要素模型假设每一种特定要素只能被用于一个生产部门:资本只能用来生产制造品,土地只能用来生产粮食,只有劳动可以用于各部门的生产。
因此,要分析一国的生产可能性,我们只需知道当劳动从一个部门转移到另一个部门时,制造品和粮食的产出组合是怎样变化的。
这个问题可能用画图的方法解决。
首先画出生产函数( 图2-14 和图2-15) ,然后将这两条曲线且合起来导出生产可能性边界。
图2-14 表明了劳动投入与制造品产出之间的关系。
给定一个资本投入量,劳动投入越多,制造品的产出就越大。
在图2-14 中,曲线Q M (K ,L M ) 的斜率表示边际劳动产出,即图2-14 制造品的生产函数图2-15边际劳动产出多投人1 人小时的劳动所增加的制造品的产出。
但是,如果只增加劳动投入而不增加资本投入,会产生边际报酬递减效应。
增加一个工人意味着每个工人操作的资本量减少,因此每单位相继增加的劳动所带来的产出增加都比上一个要少。
边际报酬递减可以从生产函数的形状上反映出来。
随着劳动增加,曲线Q 。
(K ,LM) 变得逐渐平缓,即投入的劳动越多,边际劳动产出就越小。
图2-15 以不同的方式体现了上述内容:在图中,我们直接将边际劳动产出表示为劳动投入量的函数。
类似的一对图可以表示粮食的生产函数。
将这向幅图结合起来:则可以导出一国的生产可能性边界( 见图2-16) 。
在图2-16 中,生产可能性边界说明在给定制造部门产出的情况下能生产多少粮食,反之亦然。
图2-16 特定要素模型中的生产可能性边界图2-16 是一张四象限图。
第四象限中的曲线就是前面图2-14 中的制造品的生产函数曲线。
但是在这里,我们将图2-14 颠倒了:沿竖轴向下表示在制造品生产中投入的劳动增加,沿横轴向右表示制造品产出的增加。
第二象限中是相应的粮食的生产函数曲线,这张图也是倒转的。
沿横轴向左表示在粮食中投入的劳动增加,沿竖轴向上表示粮食产出的增加。
第三象限表示一国的劳动配置情况。
劳动投入的衡量与平常的方向相反:沿竖轴向下表示在制造品生产中投入的劳动增加,沿横轴向左表示在粮食生产部门投入的劳动增加。
一个部门的劳动投入增加意味着另一部门的劳动投入减少,因此劳动配置的可能情况可以用一条向下斜倾的直线来表示。
这条直线,即直线AA ,与两轴成45 度角向下倾斜。
也就是说这条直线的斜率为-1 。
为什么这条直线代表了所有可能的劳动配置情况呢?我们注意到如果所有的劳动都用于生产粮食,L F 就等于L ,L M 等于0 。
如果将劳动逐渐地向制造品部门转移,每转移1 人小时的劳动将使L M 增加一个单位,同时使L F 减少一个单位。
这亲一直到所有的劳动都转移到制造品部门,转移所形成的点(L F ,L M ) 的轨迹是一条斜率为-1 的直线。
因此任何一种特定的劳动配置情况,都可以用直线AA 上的一点来表示,如点2 。
现在让我们来看一下在劳动配置情况一定时,如何确定各产品的产出。
假定第三象限的点2 表示过去的配置情况,即有K 单位的劳动用于制造品生产,单位的劳动用于粮食生产。
然后我们采用各部门的生产函数曲线来确定产出:制造品的产出为,粮食的产出为。
和所确定的第一象限的点2' 就表明了制造品和粮食的最后产出情况。
要描画出整条生产可能性边界,只需在不同劳动配置情况下重复上述过程。
我们可以从在粮食生产中投入劳动最多的那一点开始,即第三象限的点1 ,然后逐渐增加在制造品生产中投入的劳动,直到用于生产粮食的劳动变得非常少,如点3 所示。
第一象限据此得出相应的点,从点1' 点到3' 勾画出了一条曲线。
因此第一象限的曲线PP 表明在给定土地、劳动和资本总量时,一个国家的生产可能性。
在李嘉图模型中,劳动是唯一的生产要素,生产可能性边界是一条直线,即用粮食衡量的制造品机会成本是不变的。
然而在特定要素模型中,其他生产要素的加入使生产可能性边界PP 变为一条曲线。
曲线PP 的弯曲反映了各部门劳动的边际报酬递减规律。
边际报酬递减是特定要素模型和李嘉图模型的关键区别。
在绘制曲线PP 线,我们假定劳动从粮食部门转向制造品部门。
如果将1 人小时的劳动从粮食部门转向制造部门,这一额外投入会使制造品的产出增加,增加的量就是制造品部门的劳动边际产量MPLM 人小时的劳动。
同时,从粮食生产中每转移出l 单位的劳动,将使粮食的和出减少,减少的量等于粮食部门的劳动边际产量MPLF 。
因此要增加l 单位制造品的产出,就必须减少MPL F /MPL M 单位的粮食产出。
所以曲线PP 的斜率也是用粮食的衡量的制造品的机会成本,也就是为增加1 单位制造品的产出所必须牺牲的粮食产量:生产可能性曲线斜率= -MPL F /MPL M现在我们明白了为什么曲线PP 是弓形的。
当我们从点l 移动到点3 时,L M 增加而L F 减少。
然而如图2-15 所示,当LM 增加时,制造品部门的边际劳动产出减小。
相应地,当L F 减少时,粮食部门的边际劳动产出增大。
所以曲线PP 从左向右变得越来越陡。
三、价格、工资和劳动配置各部门分别会投入多少劳动呢? 要回答这一问题就必须来看一下劳动市场的供求状况。
每个部门对劳动的需求取决于本部门产品的价格和工资率,而工资率又取决于制造品和粮食两个部门对劳动的总需求。
在制造品和粮食的价格以及工资率给定时,我们就能确定各个部门的劳动投入量和产出。
首先,我们来看一看劳动的需求。
各部门都要追求利润最大化,因此当增加的1 人小时的劳动所生产的价值等于雇佣1 人小时所需的费用时,对应的劳动投入量就是各部门对劳动的需求。
例如,在制造品部门,增加的1 人小时的劳动所生产的价值等于制造品部门边际劳动产出乘经制造品的单位价格:MPL M ×P M ,劳动的工资率为W 。
各部门雇佣劳动,直到边际劳动产值等于工资率为止,即:MPL M ×P M =W由于边际报酬递减,制造品部门的边际劳动产出,是一条向下倾斜的曲线( 如图2-15 所示) 。
对应于任何给定的制造品价格,边际劳动产品的价值,即MPL M ×P M ,也应该是一条向下倾斜的曲线。
因此,我们可以用等式上式来定义制造品部门的劳动需求曲线。
如果工资率下降,其他条件不变,制造品部门会雇佣更多的劳动。
同样地,在粮食部门,增加1 人小时的劳动所生产的价值是MPL F ×P F 。
那么粮食部门的劳动需求曲线可以表示为:MPL F ×P F =W因为模型假定劳动力可以在部门问自由流动,所以两个部门的工资率W 是相等的。
也就是说,由于劳动是流动要素,它将从低工资部门向高工资部门转移,直到两个部门的工资率相等为止。
这样,工资率就可以由劳动总需求等于总供给这一条件来确定。
劳动的总供给为:L M +L F =L我们可以用图来表示上述三个等式,图2-17 有助于我们理解在给定的制造和粮食价格下,.工资率和各部门的劳动雇佣量是如何确定的。
图2-17 的横轴表示劳动总供给L 。
图左端的竖轴表示制造品部门的劳动边际产品价值,即图2-15 中的MPL M 曲线和制造品价格P M 的乘积。
曲线MPL M ×P M 也就是制造品部门的劳动需求曲线。
图右端的竖轴表示粮食部门边际劳动产品价值,曲线MPL F ×P F 也就是粮食部门的劳动需求曲线。
点1 表示均衡时的工资率和劳动在两部门之间的配置情况。
在工资率为w 时,制造品部门的劳动需求(L M ) 和粮食部门的劳动需求(L F ) 之和正好等于劳动总供给L 。
图2-17 劳动的配置从对劳动配置的分析中,我们可以清楚地看到相对价格和产出之间的关系。
这一关系可广泛地应用于特定要素模型以外的情况。
上两式表示:MPL M ×P M = MPL F ×P F =W或改写为:-MPL F /MPL M = -P M /P F上等式的左边是生产可能性边界在某一特定生产点上的斜率,等式的右边是负的制造品的相对价格。
这一结果告诉我们,在生产点上,生产可能性边界一定和一条斜率等于负的制造品价格除以粮食价格的直线相切。
图2-18 表明,如果制造品的相对伶格为(P M /P F ) ,该国就在点1 上进行生产。
图2-18 特定要素模型中的生产当粮食和制造品的价格发生变化时,劳动的配置和收入的分配又会怎样呢? 我们注意到,任何一种价格变化都可以归结为下面两者之一:P M 和P F 变化的比率相同或者P M 和P F 中只有一者发生了变化。
例如,假定制造品的价格上升了17% ,粮食的价格上升了10% ,我们来分析一下这些变化带来的影响。
首先要考虑的是,如果制造品的价格和粮食的价格都上升了10% ,会有什么影响。
然后分析如果制造品的价格单独上升了7% 会有什么影响。
这样,我们就能将总价格的变化带来的影响和相对价格变化带来的影响区分开来。
1 .价格同比率变化。
图2-19 说明P M 和P F 同比率上升所产生的影响。
P M 从上升到;P F 从上升到。
如两种产品价格都上升10% ,两条劳动需求曲线也都相应地上移10% 。
如图2-19 所示,这一移动使工资率也上升了10% ,从w 1 ( 点1) 上升到w2 ( 点2) 。