函数与几何综合题的解题方法

专题08一次函数与几何综合的五种考法类型一、等腰三角形存在性问题(1)求直线CB的解析式；(2)点E在x轴上，【答案】(1)12y x =+(2)(4,0)、(16,0)-、当10BE AB ==时，1E 点的坐标为(4,0)，2E 点的坐标为当AB AE =时，点B 与点E 是关于y 轴对称，E 当EA EB =时，设点E 坐标为(,0)x ，则2228(6)x x +=+，解得：73x =4E 点的坐标为7(,0)3，(1)当点P 在线段BO 上时，①求证：AOP BOQ ≌△△；②若点P 为BO 的中点，求△(2)在点P 的运动过程中，是否存在某一位置，的坐标；若不存在，请说明理由．当点P 在线段OB 上时，若OC OQ =，由于OP OQ =，则有在OCP △中，OPC AOP ∠=∠+OC OP ∴>，即OC OQ =不可能；若CQ OQ =，由于OP OQ =，则有过点C 作CH x ⊥轴于点H ，显然即CQ OQ =不可能，∴当COQ 是等腰三角形时，只有当点P在BO的延长线上时，同理可得：(0,424)P--，综上所述：(0,424)P-或P【点睛】本题考查了一次函数与几何图形综合，图形是解题的关键．【变式训练2】如图，在平面直角坐标系中，一次函数分别交于点B、A，点P为y(1)求点A、B的坐标；(2)当点P在y轴负半轴上，且ABP的面积为6时，求点(3)是否存在点P使得ABP为等腰三角形?若存在，求出点设()()0,0P n n <，则2PA =-所以()22224PA n n n =-=-+所以224416n n n -+=+解得3n =-，所以此时点P 的坐标为(0,3-综上所述，存在点P 使得ABP 例．如图，直线24y x =+与x 轴交于点A ，与y 轴交于点B ，点C 是OB 的中点．(1)求点C 的坐标：(2)在x 轴上找一点D ，使得ACD ABC S S = ，求点D 的坐标；(3)在x 轴上是否存在一点P ，使得ABP 是直角三角形？若存在，请写出点P 的坐标；若不存在，请说明理由．【答案】(1)()0,2C (2)点D 的坐标为()4,0-或()0,0(3)存在，满足条件的P 点的坐标为()0,0或()8,0(1)填空：b =，m =，k =；(2)如图2，点D 为线段BC 上一动点，将ACD 沿直线AD 翻折得到AED △，线段AE 交轴于点F ．①求线段AE 的长度；②当点E 落在y 轴上时，求点E 的坐标；③若DEF 为直角三角形，请直接写出满足条件的点D 的坐标．【答案】(1)8，2-，12-(2)①45；②点E 的坐标为()0,4219-；③点D 的坐标为()20，或()254,0-【分析】（1）根据待定系数法求解即可；（2）①过点A 作AH y ⊥轴于点H ，作AG x ⊥轴于点G ，根据勾股定理得到()222262480AE AC ==++=，于是得到结论；②利用勾股定理求出219HE =，可得2194OE =-，即可得答案；③分两种情况讨论，当90EDF ∠=︒时，求出135ADC ∠=︒，得45ADO ∠=︒，得DG AD ==得点D 坐标；当90DFE ∠=︒时，设DF x =，则8DE DC x ==-，由勾股定理得：()()2228454x x -=+-，求出DF ，得点D 坐标．【详解】（1）解：把()40B -，代入2y x b =+，∵()024b =⨯-+，∴8b =，∴直线AB ：28y x =+，把()4A m ，代入28y x =+，∴2m =-，∵ACD 翻折得到AED△∴()222262480AE AC ==++=，∴45AE =②当E 点落在y 轴上时，在Rt AHE △中，∵222AE AH HE -=∴222802HE AE AH =-=-=∴2194OE HE OH =-=-，∴点E 的坐标为()04219-，；③如下图，当90EDF ∠=︒时，由翻折得ADC ∠∴1359045ADO ∠︒︒=-=︒，∵4AG =，∴4DG AG ==，∴422OD DG OG =-=-=，∴点D 的坐标为()20，；如下图，当90DFE ∠=︒时，80AE AC ==设DF x =，则8DE DC x ==-，在Rt DEF △中，由勾股定理得：(解得：252x =-，∴254OD DF OF =-=-，∴点D 的坐标为()254,0-，综上，点D 的坐标为()20，或(2【点睛】本题考查了一次函数的综合题，勾股定理，角平分线的性质，直角三角形的性质和判定，翻折的性质，解题的关键是作辅助线．(1)如图1，求出AOP 的面积；(2)如图2，已知点C 是直线85y x =上一点，若APC △是以AP 为直角边的等腰直角三角形，求点C 的坐标．【答案】(1)AOP 的面积为40(2)点C 的坐标为()1016，或162,⎛⎫⎪∵直线l x ∥轴，点B ∴8PH OB ==，∴12AOP S OA PH == 故答案为：40；（2）设点(),8P n (n ≠过点P 作直线FE ，交APC 为等腰直角三角形，则90APE FPC ∴∠+∠=︒，APE FCP ∴∠=∠，90PEA CFP ∠=∠=︒ ，(AAS)PEA CFP ∴ ≌，同理可得：(AAS)AMP ANC ≌AM AM ∴=且MP NC =，8|10|m ∴=-或8105n m -=解得：2565m n =⎧⎪⎨=⎪⎩或181945m n =⎧⎪⎨=⎪⎩(1)求直线l 的解析式；(2)求证：ABC 是等腰直角三角形；(3)将直线l 沿y 轴负方向平移，当平移恰当的距离时，直线与在直线CD 上存在点P ，使得A △的坐标．【答案】(1)142y x =-+∴90DPE A PB ''∠=∠=︒，∴A PD B PE ''∠=∠，∵90A FP CEB ''∠=∠=︒，∴A FP CEB '' ≌，∴4,PE PF A F B E ''===，此时点P 的坐标为()44--，；如图，若以点P 为直角顶点时，过点同理此时点P 的坐标为()44-，；如图，若以点B '为直角顶点时，过点P 作同理A OB B GP ''' ≌，∴44OB PG OF t '====+，B '∴8t =-或0（舍去），∴8B G OA ''==，∴12OG =，∴此时点P 的坐标为()412--，；如图，若以点B '为直角顶点时，过点B '作B M CD '⊥轴于点M ，则4B M OF '==，OB MF '=，同理PB M A B O ''' ≌，∴44B M B O t ''===+，82PM OA t '==+，∴0=t （舍去）；如图，若以点A '为直角顶点时，同理A PF B A O ''' ≌，∴,PF A O B O A F '''==，∴4482t t --=---，解得：8t =-，∴8PF =，此时点P 的坐标为()48-，；如图，若以点A '为直角顶点时，同理A PF B A O ''' ≌，∴,PF A O B O A F '''==，∴4824t t --=++，解得：163t =-，∴83PF =，∴此时点P 的坐标为84⎛⎫--，；(1)①A 的坐标是_____________②求直线AB 的表达式；(2)点P 是直线y =(3)当ABP 为等腰直角三角形时，请直接写出【答案】(1)①(0,3【分析】（1）把x（3）解：如图1，当点P 为顶点时，过点P 作PE x ⊥轴，过点A 作AF 垂直于PE 的延长线于点F ，∵ABP 是等腰直角三角形，AP PB ∴=，APB ∠=90︒，=90FAP APF +∠︒ ，=90APF BPE ∠+∠︒，=FAP BPE ∴∠∠，在AFP 和PEB △中，F E FAP EPB AP PB ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AFP PEB AAS ∴≅ ，AF PE ∴=，BE PF =，===90O F E ∠∠∠︒ ，∴四边形AOEF 是矩形，==AF PE OB BE ∴+，===AO FE FP PE BE PE ++，==2AO BE OB BE BE OB +++，()0,3A 、()1,0B ，=3AO ∴，1OB =，21=3BE ∴+，=1BE ∴，==31=2PE AO BE --，==11=2OE OB BE ∴++，∴点P 的坐标为()2,2；如图2，当点B 为顶点时，过点P 作PG x ⊥轴，ABP 是等腰直角三角形，AB BP ∴=，=90ABO OAB ∠+∠︒ ，=90ABO PBG ∠+∠︒，=OAB PBG ∴∠∠，在AOB 和BGP 中，O PGB OAB PBG AB BP ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AOB BGP AAS ∴≅ ，=PG OB ∴，BG AO =，()0,3A 、()1,0B ，=3AO ∴，1OB =，==13=4OG OB BE ∴++，=1PG ，∴点P 的坐标为()4,1；如图3，当点A 为顶点时，过点P 作PM y ⊥轴，PAB △是等腰直角三角形，PA AB ∴=，=90PAB ∠︒，90MAP OAB ∠+∠=︒ ，90MAP MPA ∠+∠=︒，=MPA OAB ∴∠∠，在PMA △和AOB 中，M O MPA OAB AP AB ∠=∠⎧⎪∠=∠⎨⎪=⎩()PMA AOB AAS ∴≅ ，=MP AO ∴，=MA OB ，()0,3A 、()1,0B ，=3AO ∴，1OB =，3MP ∴=，==13=4OM MA AO ++，∴点P 的坐标为()3,4，故答案为：()2,2；()4,1；()3,4．【点睛】本题考查了一次函数的综合运用，等腰直角三角形的性质和矩形的性质及全等三角形的性质的判定，熟练求一次函数的解析式和构造全等三角形是解题的关键．类型四、全等问题(1)点A坐标为________，点B坐标为(2)当BOP△的面积是4时，求点(3)在y轴上是否存在点Q，使得以接写出所有符合条件的点P的坐标，否则请说明理由．【答案】(1)(3,0)，(0,4)，12 5(2)4(2,)20(2,)125OM OQ ==，12(0,)5Q 或12(0,)5-，6(5P ，12)5或24(5，12)5-；②如图3，图4，当OMP PQO ≌△△时，125PQ OM ∴==，12(5P ∴-，36)5或12(5，4)5；综上所述：P 点坐标为(65，12)5或24(5，12)5-或12(5-，36)5或12(5，4)5．【点睛】本题考查一次函数的图象及性质，判定及性质，分类讨论，数形结合是解题的关键．【变式训练1】如图，一次函数364y x =+的图象与于点C ，点P 在直线AB 上运动，点Q 在(1)求点A ，B 的坐标；(2)求OC 的长；(3)若以O ，P ，Q 为顶点的三角形与【答案】(1)()8,0A -，(B (3)Q 的坐标为120,5⎛⎫ ⎪⎝⎭或0,⎛ ⎝则OC PQ=，∴245PQ =，∴245m=-，∴33241266 4455m⎛⎫+=⨯-+=⎪⎝⎭，∵PQ OC=，∴245 PQ=．∴245=m，∴33244866 4455m+=⨯+=，∴48 0,5Q⎛⎫ ⎪⎝⎭；则245 OQ OC==，∴240,5Q⎛⎫ ⎪⎝⎭；综上所述，Q的坐标为12 0,5⎛⎫ ⎪⎝⎭或(1)求点B 的坐标及直线BC 的函数表达式；(2)在坐标系平面内，存在点D ，使以点A ，B ，D 为顶点的三角形与ABC 全等，画出ABD ，并求出点D 的坐标．【答案】(1)点B 的坐标为(0，3)，33y x =-+；(2)图见解析，点D 的坐标为(4-，3)或(3-，4)或(0，1)-．【分析】（1）将点点(3A -，0)代入解析式得出3b =，继而得出点B 的坐标为(0，3)，根据:3:1OB OC =得出1OC =，即点C 的坐标为(1，0)，然后待定系数法求解析式即可求解；（2）分在x 轴上方：BAD ABC ≌和(ABD ABC ≌如图1)和点D 在y 轴上(如图②)两种情况，根据全等三角形的性质即可求解．【详解】（1）解：∵直线AB ：y x b =+过点(3A -，0)，03b ∴=-+，3b ∴=．当0x =时，3y x b b =+==，∴点B 的坐标为(0，3)，即3OB =．OB ：3OC =：1，1OC ∴=．点C 在x 轴正半轴，∴点C 的坐标为(1，0)．设直线BC 的解析式为()0y kx c k =+≠，将(0B ，3)、(1C ，0)代入y kx c =+，得：30c k c =⎧⎨+=⎩，解得：33k c =-⎧⎨=⎩，∴直线BC 的函数表达式为33y x =-+．（2）分在x 轴上方：BAD ABC ≌和(ABD ABC ≌如图1)和点D 在y 轴上(如图②)两种情况考虑：如图①：①当BAD ABC ≌时，3OA OB == ，45BAC ∴∠=︒．BAD ABC ≌，45ABD BAC ∴∠=∠=︒，4BD AC ==，BD ∴∥AC ，∴点D 的坐标为(4-，3)；②当ABD ABC ≌时，45BAD BAC ∠=∠=︒，4AD AC ==，90DAC ∴∠=︒，∴点D 的坐标为(3-，4)．如图②当ABD BCA ≌时，4BD AC ==，1OD ∴=，∴点D 的坐标为(0，1)-．综上所述，点D 的坐标为(4-，3)或(3-，4)或(0，1)-．【点睛】本题考查了一次函数与几何图形，坐标与图形，全等三角形的性质与判定，数形结合是解题的关键．【变式训练3】如图①，已知直线24y x =-+与x 轴、y 轴分别交于点A 、C ，以OA OC ，为边在第一象限内作长方形OABC ．类型五、角度之间关系过点P 作EF y ⊥轴于点E ，过点H 作∴45POG ∠=︒，∵()3,1P ，∴1,3EP OE ==∵OA OB =，45AOB ∠=︒∴AOB 是等腰直角三角形，∵45APO EOP ∠+∠=︒，PQO APO∠=∠∴45PQO EOP ∠+∠=︒又∵9045EOP GOQ POG ∠+∠=︒-∠=∴GOQ GQO∠=∠∴GQ GO =，即点G 在OG 的垂直平分线上，∵90OEP PFH OPH ∠=∠=∠=︒，∴90OPE FPH PHF ∠=︒-∠=∠，(1)求直线AB的关系式；(2)连接PD，当线段PD AB⊥时，直线AD上有一点动M∴1284,2525S ⎛⎫-- ⎪⎝⎭，∵45,DKR DAO KT RK ∠=∠=︒⊥∴45DKR DKT ∠=︒=∠，∴KT KP =，∴P ，T 关于直线AD 对称，连接TS 交AD 于M ，交x 轴于N 4y x =-+12x =-得y =∵3,4OB OA ==，∴34PH PH AH HW==，设3PH t =，则4AH HW t ==∴5PW t OW ==，∵4OW HW AH OA ++==，∵12POA BAO ∠=∠，∴2POA APO POA ∠+∠=∠∴APO POA ∠=∠，∴4AO AP ==，∵34PF OB AF AF ==，∴165AF =36(1)求直线BC 的函数解析式；(2)设点M 是x 轴上的一个动点，过点M 作y 轴的平行线，交直线于点Q ．①若PQB △的面积为83，求点M 的坐标．②连接BM ，如图2，在点M 的运动过程中是否存在点P ，使∠求出点P 坐标，若不存在，请说明理由．则113(3)22PQ m m m =-+-+=，则PQB ∆的面积21122PQ BD m =⋅=故点M 的坐标为43(3，0)或4(-②如图，当点M 在y 轴的左侧时，点C 与点A 关于y 轴对称，AB BC ∴=，BAC BCA ∴∠=∠，BMP BAC ∠=∠ ，BMP BCA ∴∠=∠，90BMP BMC ∠+∠=︒ ，90BMC BCA ∴∠+∠=︒(1)求点A，B的坐标；(2)若直线AC⊥AB交y轴负半轴于点(3)在y轴上是否存在点P，使以求出点P的坐标；若不存在，请说明理由．【答案】(1)A(−1，0)；B(0，2)(2)1.25；(3)y轴上存在点P，使以A，当BA＝BP时，BP＝∴点P1的坐标为(0，当PB＝PA时，设OP ∴(2−x)2=1+x2，解得：∴点P3的坐标为(0，当AB＝AP时，OP＝∴点P4的坐标为(0，综上所述：y轴上存在点标为(0，2+5）或(0(1)填空：=a ______，b =______；(2)在射线CD 上有一动点E ，过点E 作EF 平行于y 轴交直线AB 时，求点E 的坐标；(3)点M 为直线AB 上一点，且45CDM ∠=︒，求点M 的坐标．【答案】(1)1，2-1112132⎛⎫∴90QCP QPC ∠+∠=︒，∵CP CD ⊥，∴90QCP DCL ∠+∠=︒∴QPC DCL ∠=∠，∴QPC LCP ≌△△，∵()1,1C -，()0,2D -，∴CG HK =，GH KD =，∵()1,1C -，()0,2D -，设(,H c d ∴2c =-，1d =-，∴()2,1H --，可得直线DH 的解析式为联立12213y x ⎧=--⎪⎪⎨，解得721x ⎧=-⎪⎪⎨(1)求点C的坐标；∥轴交AB于点(2)如图2，过点C作直线CD x①求线段CD的长；②在坐标平面内，是否存在点M（除点B外），全等？若存在，请直接写出所有符合条件的点M DC≌△BDC时，当△1M和点B关于直线则点1M的坐标为：（-1∴点1M CD≌△BDC时，当△2。

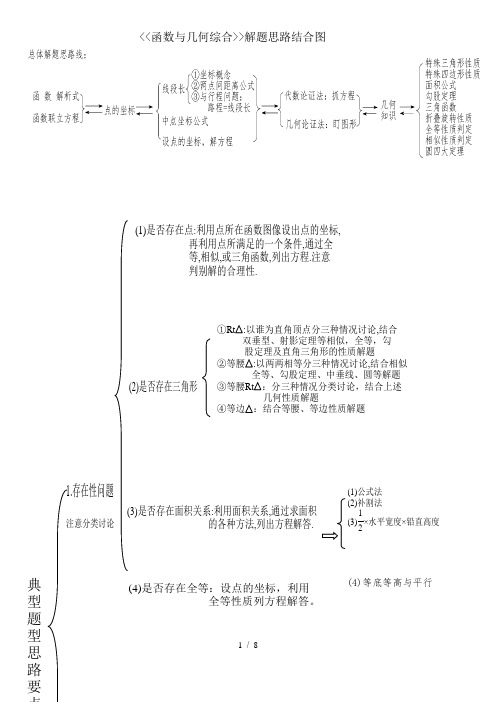
<<函数与几何综合>>解题思路结合图(1)公式法(2)补割法(3)12×水平宽度×铅直高度注意分类讨论1.存在性问题(1)是否存在点:利用点所在函数图像设出点的坐标, 再利用点所满足的一个条件,通过全 等,相似,或三角函数,列出方程.注意 判别解的合理性.典型题型 (2)是否存在三角形①Rt :以谁为直角顶点分三种情况讨论,结合 双垂型、射影定理等相似，全等，勾 股定理及直角三角形的性质解题②等腰:以两两相等分三种情况讨论,结合相似 全等、勾股定理、中垂线、圆等解题③等腰Rt ：分三种情况分类讨论，结合上述 几何性质解题④等边：结合等腰、等边性质解题(3)是否存在面积关系:利用面积关系,通过求面积 的各种方法,列出方程解答.(4)是否存在全等：设点的坐标，利用 全等性质列方程解答。

(4)等底等高与平行(5)是否存在相似:一般利用等角分两种情况分类讨论,利用相似性质列方程解答(7)是否存在矩形、菱形、正方形：结合点的坐标， 利用它们的判定或性质及相似等列方程解答。

2.最值问题(1)线段最值①求解析式,利用二次函数配方求最值; ②垂线段最短、两点间线段最短 （转化为同一线段、将军饮马问题）(2)线段和差或周长最值:①解析式求最值;②将军饮马问题(3)面积最值:利用面积三种方法,列解析式求最值3.取值范围问题:①善于抓住图形位置特点,确定最大/小值; ②求解析式解不等式方程.4.线段定值问题:①直接计算；②如果题目没给出定值的，可利用特殊位置、 极端位置先探求出定值，然后加以一般化证明。

(6)是否存在平行四边形①几何论证法：以已知边为长边、短边及对角线去找图②代数论证法：选三点，以两两的连线为对角线，利用中点坐标公式分三种情况讨论计算出第四点坐标③平行四边形顶点的横纵坐标的差相等，利用平移表示 各点坐标，计算上可以简化，用于表示各顶点坐标①点动:依解析式设动点坐标②线动总体思路:圆只是周围是曲线的多边形 全等或相似勾股等照常用①求角或三角函数:直接求或等量替换 圆心或圆周角定理 切线性质,内接四边形对角性质 弦切角性质②求线段:垂径定理 切线性质③辅助线:(1)连半径，构造等腰(2)见弦必做弦心距，构造RT △(3)见切线必连圆心与切点，构造RT △ (4)见直径，构造90°圆周角基本思路:在变化中找到不变的性质③面动:折叠,平移,旋转5.动态问题6.圆典型题型思路要点与行程问题结合的动态问题:先用字母表示出各线段,根据 各线位置,结合相似全等等几 何知识列方程解答题型解读1 二次函数与几何综合题的两种解题方法【分析思路】在二次函数与几何综合的各种题型中，只有一条总体分析思路线：解析式（方程）←→点的坐标←→线段长←→几何问题，但在具体解题分析过程中，求点的坐标或线段长时，思考方向却有两种：可以由左往右思考，即“由解析式或方程求点的坐标，由点的坐标求线段长”，这是“代数论证方法”；也可以由右往左思考，即“由几何问题求线段长，由线段长求点的坐标”，这是“几何论证方法”。

一次函数几何综合题解题技巧一次函数是初中数学的重点知识之一，同时也是中考的热点。

它与几何知识的综合应用在中考中主要体现在：利用一次函数求待定系数、一次函数图象与几何图形相结合、一次函数图象的应用等几个方面。

本文将结合实例谈谈一次函数与几何图形综合题的解题技巧。

一、利用一次函数求待定系数解决这类问题的关键是利用已知条件建立方程组，求出待定系数。

具体来说，一般先设出一次函数解析式，利用已知条件得到解析式中的系数，再得到一次函数解析式。

【例1】已知：如图1，在平面直角坐标系中，直线AB与两坐标轴分别交于A、B两点，且与反比例函数的图象在第一象限交于点C。

（1）求该反比例函数的解析式；（2）求直线AB的解析式；（3）根据图像，当C的横坐标在哪个取值范围内时，线段AB不经过第四象限？分析：（1）由点C在反比例函数图象上，可直接求得解析式；（2）由于点C在直线AB上，可设直线AB的解析式为，将点C 的坐标分别代入解析式，可求得A、B两点的坐标，进而可求得直线AB 的解析式；（3）由图象可知，当C点的横坐标小于时，线段AB不经过第四象限。

解：（1）设反比例函数的解析式为，将点C（3，4）代入得，所以该反比例函数的解析式为；（2）设直线AB的解析式为，因为点C（3，4）在直线AB上，所以，解得，所以直线AB与轴交于点D（6，0），又因为点A（－3，－4），所以直线AB的解析式为；（3）由图象可知，当C点的横坐标小于时，线段AB不经过第四象限。

二、一次函数图象与几何图形相结合此类问题主要利用了待定系数法、数形结合的思想以及分类讨论的思想。

解题时要注意数形结合，根据已知条件建立方程或不等式，结合图形加以分析。

【例2】如图2，在平面直角坐标系中，四边形OABC为矩形，点A、C的坐标分别为（4，0）、（0，2），点D是边BC上的一个动点（点D与B、C不重合），过点D的抛物线经过点A、C、E。

（1）求该抛物线的解析式；（2）当AC为何值时，四边形DEOB为平行四边形？请说明理由；（3）设点D的坐标为（x，y），①试求该抛物线的对称轴及点D 到直线AC的距离；②试探究在抛物线上是否存在点M，使四边形AMDE 的面积最大？若存在，请求出点M的坐标；若不存在，请说明理由。

一次函数与几何图形综合题(含答案)近日，举行了一次关于一次函数与几何图形综合的专题讲座。

在思想方法方面，介绍了函数方法和数形结合法。

函数方法是通过观察运动和变化来分析数量关系，并将其抽象升华为函数模型，从而解决问题的方法。

数形结合法则是将数与形结合起来，分析研究并解决问题的一种思想方法，对于与函数有关的问题，使用数形结合法能够事半功倍。

在知识规律方面，讲座介绍了常数k和b对直线y=kx+b(k≠0)位置的影响。

当b大于0时，直线与y轴的正半轴相交；当b等于0时，直线经过原点；当b小于0时，直线与y轴的负半轴相交。

当k和b异号时，即b大于0时，直线与x轴正半轴相交；当k和b同号时，即k和b的乘积小于0时，直线与x轴负半轴相交。

当k大于0且b大于0时，图象经过第一、二、三象限；当k大于0且b等于0时，图象经过第一、三象限；当b大于0且b小于0时，图象经过第一、三、四象限；当k小于0且b大于0时，图象经过第一、二、四象限；当k小于0且b等于0时，图象经过第二、四象限；当b小于0且b小于0时，图象经过第二、三、四象限。

讲座还介绍了直线y=kx+b(k≠0)与直线y=kx(k≠0)的位置关系。

当b大于0时，将直线y=kx向上平移b个单位，即可得到直线y=kx+b；当b小于0时，将直线y=kx向下平移|b|个单位，即可得到直线y=kx+b。

另外，当k1不等于k2时，y1与y2相交；当k1等于k2且b1不等于b2时，y1与y2平行但不重合；当k1等于k2且b1等于b2时，y1与y2重合。

最后，讲座还通过一个例题对知识规律进行了精讲。

题目是直线y=－2x+2与x轴、y轴交于A、B两点，C在y轴的负半轴上，且OC=OB。

要求求出AC的解析式。

的性质，需要灵活运用几何知识和代数知识。

在解答过程中，要注意清晰的逻辑思路和准确的计算，避免出现错误。

2) 在OA的延长线上任取一点P，作PQ⊥BP，交直线AC于Q。

我们来探究一下BP与PQ的数量关系，并证明结论。

中考数学函数与几何综合题备考策略及教学建议发布时间：2021-09-03T09:36:28.833Z 来源：《中国教师》2021年9月作者：郭兴淑[导读]郭兴淑云南腾冲市第一中学中图分类号：G652.2 文献标识码：A 文章编号：ISSN1672-2051 （2021）9-161-02一、题型分析二次函数与几何图形的综合题通常设3问，第一问主要是二次函数解析式及点坐标的求解，第二、三问就会涉及探究性问题，综合性强，难度较大，解答时往往要用到分类讨论和数形结合的思想。

类型一：探究特殊三角形的存在性特殊三角形：等腰三角形、直角三角形、等腰直角三角形、等边三角形等。

此类题常给出固定的两点，以求另外一个动点使三角形为特殊三角形。

一般步骤为：1、假设点存在并根据动点满足的条件设出点的坐标；2、分别用所设的变量表示出三个点的坐标，进而用两点间的距离公式表示出所求三角形三边的线段长度；3、再根据三角形的特殊性的性质分情况列出方程解出点的坐标。

注：若上述方法不能解决，也可适当作垂线，用勾股定理或相似建立等量关系。

类型二：探究特殊四边形的存在性特殊四边形：平行四边形、菱形、矩形、正方形等。

此类题中常给出固定的三点或两点，以求一个或两个动点使四边形为特殊四边形，一般步骤为：1、先假设结论成立，从而设出点的坐标，表示（求出）边长；2、建立关系式并计算：（1）若四边形的四个顶点位置都已经确定，可直接利用四边形的性质进行计算；(2)若四边形的四个顶点位置不确定，则需分类讨论：①以已知线段为平行四边形的某一边，画出所有符号条件的图形，利用平行四边形的性质建立关系式进行计算；②以已知线段为平行四边形的对角线，画出所有满足条件的图形，利用平行四边形对角线互相平分（中点坐标不变）建立关系式进行计算。

探究菱形、矩形、正方形时，思路与探究平行四边形一致，只需在计算时结合自身特有的性质即可。

类型三：探究相似三角形的存在性此类题一般给出一个已知三角形，求是否存在点使得另一个三角形与已知三角形相似，通常不会明确指出两个三角形的对应角、对应边，所以解答时要具备分类讨论和数形结合的思想，一般步骤为：1、假设结论成立，同时确定已知三角形的形状（三边的长度或内角的度数）2、观察动态三角形中是否存在与已知三角形相等的角，若存在，分两种情况讨论相等角的两夹边成比例即可或题目中给出了一组对应边，也只需分两种情况讨论另外两条边成比例即可；3、若动态三角形与已知三角形既没有相等的角，也没有对应边，则分三大类情况讨论。

<<二次函数与几何综合>>题型解读3 二次函数几何综合题中求直线表达式的两种解题思路【解题方法】一.用“待定系数法”求某直线的表达式1.直接求-----找出该直线上二点的坐标，直接运用“待定系数法”求该直线的表达式；2.间接求-----设置或构造某直线上的第三点及求出该点坐标，再与另一已知点的坐标结合，运用“待定系数法”求该直线的表达式；二.利用平行或垂直关系求某直线的表达式1.平行关系-------当两直线平行时，它们的K值会相等或不变；2.垂直关系-------当两直线垂直时，它们的K值互为负倒数；【范例精讲】例1.如图，抛物线y=−√39x2+2√33x+3√3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ．过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E，连接PD，与BC交于点F．设点P的运动时间为t秒（t＞0）．（1）求直线BC的函数表达式；（2）①直接写出P，D两点的坐标（用含t的代数式表示，结果需化简）②在点P、Q运动的过程中，当PQ=PD时，求t的值；（3）试探究在点P，Q运动的过程中，是否存在某一时刻，使得点F为PD的中点？若存在，请直接写出此时t的值与点F的坐标；若不存在，请说明理由．解：（1）由y=0得﹣x2+x+3=0，解得：x1=﹣3，x2=9，∴B（9，0），由x=0得y=3，∴C（0，3），设直线BC的解析式为y=kx+b，∴，∴，∴直线BC的解析式为y=﹣x+3；（2）①过p作PG⊥x轴于G，∵A（﹣3，0），C（0，3），∴OA=3．OC=3，∴tan∠CAO=，∴∠CAO=60°，∵AP=t，∴PG=t，AG=t，∴OG=3﹣t，∴P（t﹣3，t），∵DQ⊥x轴，BQ=2t，∴OQ=9﹣2t，∴D（9﹣2t，﹣t2+t），②过P作PH⊥QD于H，则四边形PGQH是矩形，∴HQ=PG，∵PQ=PD，PH⊥QD，∴DQ=2HQ=2PG，∵P（t﹣3，t），D（9﹣2t，﹣t2+t），∴﹣t2+t=2×t，解得：t1=0（舍去），t2=，∴当PQ=PD时，t的值是；（3）∵点F为PD的中点，∴F的横坐标为：（t﹣3+9﹣2t）=﹣t+3，F的纵坐标为（t﹣t2+ t）=﹣t2+t，∴F（﹣t+3，﹣t2+t），∵点F在直线BC上，∴﹣t2+t=﹣（﹣t+3）+3，∴t=3，∴F（，）．例2.如图，已知抛物线y=ax2+bx+3交x轴于点A（x,0），B（-1,0），且x>0, OA2+OB2=10，交y轴于点C. （1）求抛物线的解析式；（2）第一象限内，在抛物线上是否存在一点E，使∠ECO=∠ACB？若存在，求出点E的坐标；（3）直线y=kx(k<0)交直线y=x-3于点P，交（1）中抛物线于M，过M作x轴的垂线于点D，交直线y=x−3于N，问：△PMN能否为等腰三角形？若能，求出k的值，若不能，说明理由。

二次函数与几何图形综合题解题技巧一、求二次函数解析式。

根据y=mx+b，把一元二次方程mx+b=0化为ax+by+c=0的系数a=b，然后通过解方程得出y=mx+b的值，由于不知道b、 a的具体值，可以通过函数与几何图形的综合分析来得到它们的大致范围。

例如，已知点（ 1， 1），（ 3， -3），直线（ x， -3），（ 4， 2）;在(-3， 4)、(-1， 1)处画出一个坐标平面内关于坐标轴对称的二次函数解析式;（ 5， 2）处画出一个关于坐标轴对称的抛物线，使其解析式为y=x+b。

求这些二次函数的表达式。

1。

设二次函数解析式为y=mx+b。

分析：二次函数与一元二次方程有密切联系，解一元二次方程是解二次函数的基础。

设一元二次方程为x+b=0，则根据对称性可得，函数解析式为x+b=mx+c。

2。

设二次函数解析式为y=ax+by+c。

分析： a、 b、 c都是实数，且a>0，b>0。

设函数解析式为x+b=ax+by+c，代入上式可得， y=x+b/c=mx+c/c。

求出二次函数的解析式，即可求出a、 b、 c的值。

3。

设二次函数解析式为y=ax+by+c。

分析：根据对称性，可得y=bx+c， a、 b、c均为实数，且a>0， b>0。

设函数解析式为x+b=bx+c，代入上式可得， y=x+b/c=mx+c/c。

4。

设二次函数解析式为y=ax+by+c。

分析：解方程得y=mx+c，由对称性，得x+c=y+b，代入上式，可得， y=x+b/c。

二、用几何图形解题。

二、用几何图形解题，最好能画出这些图形的图像，再列式解答。

因为几何图形看似复杂，但并不难，常见的如圆的周长、扇形面积、矩形的面积等等。

以下是应用这两种方法解二次函数综合题的例子，供同学们参考： 1。

求出二次函数的解析式，画出抛物线y=mx+b。

分析：首先将点（ 1， 1），（ 3， -3），直线（ x， -3），（ 4， 2） ;在(-3， 4)、(-1， 1)处画出一个坐标平面内关于坐标轴对称的二次函数解析式；再设函数解析式为x+b=mx+c，代入上式得y=mx+c/c。