课堂用非线性动力学讲义第三部分
- 格式:pdf
- 大小:2.71 MB
- 文档页数:67

非线性动力学导论之四:分岔基本理论简介北京理工大学宇航学院力学系岳宝增第三章非线性动力学系统分岔基本理论一.一般系统平衡解的稳定性(1)二.平衡解的稳定流形与不稳定流形于平面摆的例子可以用来很清楚地解释全局稳定(不稳定)流形的概念;平面摆作为二阶动力学系统和谐振子极为相似。
其动力学方程为:l其中M代表质量,表示摆长,g为重力加速度,c为阻尼系数。
对时间进行尺度变换d可以得到系统的简化方程:d因为是从铅锤位置开始的角度位移,因此该变量具有周期2π;由此可知该系统的相空间为圆柱面。
我们也可以假设,从而从相图上可以观测到系统关于X的周期特性。
为了分析系统的动力学特性,首先确定系统的平衡点并研究其稳定性。
可求出系统的平衡点为:及求出系统的雅可比矩阵为:对应于平衡点有:其特征值为:如果d=0则得到特征值±i;对于较小的d值系统有共轭复根。
对应于平衡点(2kπ+π,0)系统的雅可比矩阵为:其特征值一对符号相反的实数:根据以上讨论可知:平衡点(2kπ+π,0)为鞍点,当d=0时,其对应的特征向量为:及对于较小的的d>0,平衡点(2kπ,0)为吸引子-螺旋旋线);d=0时该类平衡点所对应的是非双曲点。
由于此时系统不受摩擦(阻尼)影响,单摆将做周期运动。
因此,在平衡点附近,系统的动力学特性为:无阻尼d=0 阻尼d>0d=0时,所对应的一类周期运动是单摆做上下摆动;另一类周期运动是单摆由稳定及不稳定流形通过倒立位置位置的运动。
如果单摆几乎刚好处于倒立位置时(不稳定),它将倒回并再次回摆到几乎刚好倒立的位置。
这意味着稳定流形与不稳定流形将有如下图所示的联接:单摆沿逆时针方向穿越倒立位置。
单摆没有穿越倒立位置。
单摆沿顺时针方向穿越倒立位置。
在有阻尼的情形下,实际上所有的初始条件所确定的运动将趋于下垂平衡位置。
例外情形是稳定流形所对应的运动,由趋于倒立位置的所有点组成。
所有初始条件将终止于平衡点三.分岔的基本概念对于一个非线性方程,由于其中参量取值不同,解的形式可能完全不同,即参量取值在某一临界值两侧,解的性质发生本质变化(例如平衡状态或周期运动的数目和稳定性等发生突然变化)。







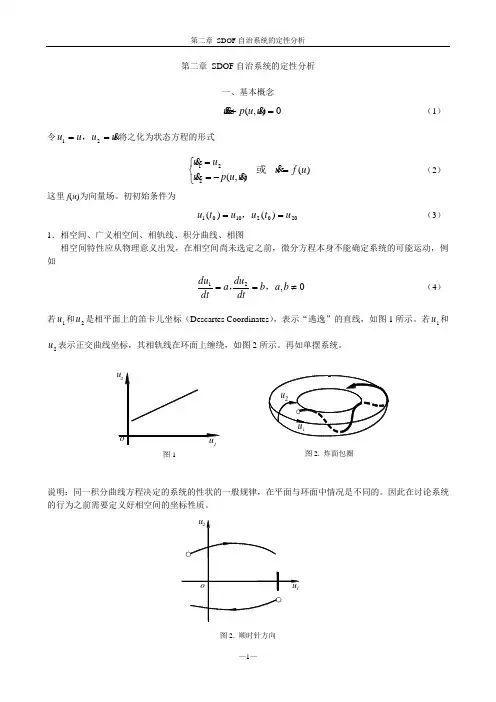
第二章 SDOF 自治系统的定性分析一、基本概念0),(=+u u p u(1)令uu u u ==21,将之化为状态方程的形式 )(),(221u f u u u p uu u=⎩⎨⎧-== 或 (2)这里f (u )为向量场。
初初始条件为20021001)()(u t u u t u ==,(3)1.相空间、广义相空间、相轨线、积分曲线、相图相空间特性应从物理意义出发,在相空间尚未选定之前,微分方程本身不能确定系统的可能运动,例如21dudu ,相图特点:(1)上半平面,021>=u u ,相轨线从左到右;(2)下半平面,021<=u u,相轨线从左到右;(3)横坐标,∞→⎪⎪⎭⎫⎝⎛=0122u du du ,轨线与横轴正交。
2.定理:若),;(00u t t u u= 是方程(2)的解,对任意常数0t ,),0;(00u t t u u -= 仍是其解。
证明:对任何时刻/t ,有()()///|)()(|)(|)(00/0t t t t t t t t t u f t t u f dtt du dt t t du =-==-=-==- (5)表明:上式在任意瞬时恒成立,故),0;(00u t t u u-= 是解。
说明:自治系统在相空间的轨线只与初始值有关,与初始时刻的选取无关。
因此,今后令00=t ,初始条件(3)成为2010)0()0(u u u u ==,(6)例1:对自治系统0=+u u,t u sin =是其解,)sin(0t t u -=还是其解。
若取t u cos -=,此时20π=t 。
推论:经过相空间中的每一点(奇点除外),自治系统有一条且仅有一条相轨线(只有唯一轨线通过)。
证明:设方程(2)有两条轨线),,(1010u t t u u =,),,(2020u t t u u =有公共点,即在时刻1T 和2T 有),,(),,(2020210101u t T u u t T u =(7)因),,(101021u t T T t u u -+=还是方程(2)的解,因此下式成立22|),,(|),,(2020101021T t T t u t t u u t T T t u ===-+(8)根据Cauchy 定理:若在),(00u t 的邻域f 对u 的偏导数存在并连续,对t 的单边偏导数存在并连续,则),(u t f u = 在相当小的区间],0[δ内存在唯一解(过同一初始值的解是唯一的)。

非线性动力学导论之四:分岔基本理论简介北京理工大学宇航学院力学系岳宝增第三章非线性动力学系统分岔基本理论一.一般系统平衡解的稳定性(1)二.平衡解的稳定流形与不稳定流形于平面摆的例子可以用来很清楚地解释全局稳定(不稳定)流形的概念;平面摆作为二阶动力学系统和谐振子极为相似。
其动力学方程为:l其中M代表质量,表示摆长,g为重力加速度,c为阻尼系数。
对时间进行尺度变换定义(或直接假设)及d可以得到系统的简化方程:d因为是从铅锤位置开始的角度位移,因此该变量具有周期2π;由此可知该系统的相空间为圆柱面。
我们也可以假设,从而从相图上可以观测到系统关于X的周期特性。
为了分析系统的动力学特性,首先确定系统的平衡点并研究其稳定性。
可求出系统的平衡点为:及求出系统的雅可比矩阵为:对应于平衡点有:其特征值为:如果d=0则得到特征值±i;对于较小的d值系统有共轭复根。
对应于平衡点(2kπ+π,0)系统的雅可比矩阵为:其特征值一对符号相反的实数:根据以上讨论可知:平衡点(2kπ+π,0)为鞍点,当d=0时,其对应的特征向量为:及对于较小的的d>0,平衡点(2kπ,0)为吸引子-螺旋旋线);d=0时该类平衡点所对应的是非双曲点。
由于此时系统不受摩擦(阻尼)影响,单摆将做周期运动。
因此,在平衡点附近,系统的动力学特性为:无阻尼d=0 阻尼d>0d=0时,所对应的一类周期运动是单摆做上下摆动;另一类周期运动是单摆由稳定及不稳定流形通过倒立位置位置的运动。
如果单摆几乎刚好处于倒立位置时(不稳定),它将倒回并再次回摆到几乎刚好倒立的位置。
这意味着稳定流形与不稳定流形将有如下图所示的联接:单摆沿逆时针方向穿越倒立位置。
单摆没有穿越倒立位置。
单摆沿顺时针方向穿越倒立位置。
在有阻尼的情形下,实际上所有的初始条件所确定的运动将趋于下垂平衡位置。
例外情形是稳定流形所对应的运动,由趋于倒立位置的所有点组成。
所有初始条件将终止于平衡点三.分岔的基本概念对于一个非线性方程,由于其中参量取值不同,解的形式可能完全不同,即参量取值在某一临界值两侧,解的性质发生本质变化(例如平衡状态或周期运动的数目和稳定性等发生突然变化)。

非线性动力学及其应用研究第一章:非线性动力学的基本概念随着科技的进步,对复杂系统的研究越来越深入。
其中,非线性动力学成为了复杂系统研究中的重要方法。
非线性动力学旨在深入探究非线性系统的复杂性质和行为。
在此了解非线性动力学的基本概念是必须的。
1.1 非线性系统和线性系统非线性系统指的是当系统输入发生变化时,输出不随输入线性变化的系统。
而线性系统指的是当系统输入发生变化时,输出随输入线性变化的系统。
其中,线性系统的特点在于:叠加原理成立、系统的响应与输入之间存在比例关系等。
而非线性系统则具有较多的复杂性质,如:非线性叠加原理、非线性稳定性等。
1.2 动力学和非线性动力学在自然科学领域中,动力学研究的是物体的运动,其研究范围涵盖着很多方面,如质点和刚体的运动、场的发展等。
而非线性动力学是描述非线性系统动态行为的工具,它将系统的演化规律显示在空间或时间的图像中,并对系统的演化过程进行研究。
第二章:非线性动力学的主要应用2.1 气象学气象学是非线性动力学的一个典型应用领域,其中对大气环流的研究尤为重要。
大气环流具有多尺度、多层次和非线性等复杂性质,如何准确地描述和预测天气、气候变化等气象现象是气象学研究的重要问题。
因此,非线性动力学的方法在气象学中得到广泛应用。
2.2 复杂网络复杂网络是由大量相互关联的节点和边构成的系统,具有重要的应用意义。
非线性动力学中的耦合振子模型和耦合映射模型等对复杂网络的模拟和分析具有重要作用。
例如,非线性动力学可以用于模拟生物神经网络、社交网络、金融市场等复杂的实际网络系统。
2.3 控制工程控制工程是一门跨学科的科学,其目的是将一些变量引导到所期望的方向,从而实现对系统的控制。
而非线性动力学可以为控制工程提供有效的理论基础和分析方法,如变结构控制理论、模糊控制理论、混沌控制理论等。
第三章:非线性动力学的发展趋势非线性动力学具有广泛的应用前景和深刻的理论内涵,其发展趋势如下:3.1 物理学领域中的深入应用非线性动力学的一些理论和模型可以应用在物理学中,如在量子力学、高能物理、介观物理、宏观物理等领域,推动了物理学的发展。