第十一章 统计学 一元线性回归

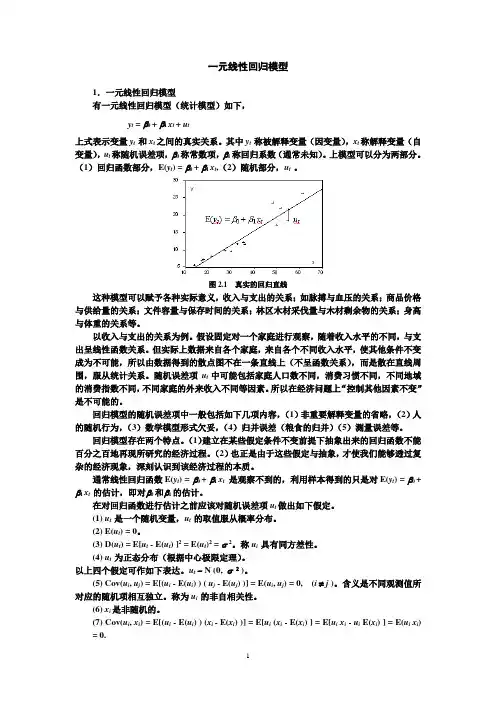
一元线性回归模型1．一元线性回归模型有一元线性回归模型（统计模型）如下，y t = β0 + β1 x t + u t上式表示变量y t 和x t之间的真实关系。

其中y t 称被解释变量（因变量），x t称解释变量（自变量），u t称随机误差项，β0称常数项，β1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t) = β0 + β1 x t,（2）随机部分，u t。

图2.1 真实的回归直线这种模型可以赋予各种实际意义，收入与支出的关系；如脉搏与血压的关系；商品价格与供给量的关系；文件容量与保存时间的关系；林区木材采伐量与木材剩余物的关系；身高与体重的关系等。

以收入与支出的关系为例。

假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。

但实际上数据来自各个家庭，来自各个不同收入水平，使其他条件不变成为不可能，所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。

随机误差项u t中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。

所以在经济问题上“控制其他因素不变”是不可能的。

回归模型的随机误差项中一般包括如下几项内容，（1）非重要解释变量的省略，（2）人的随机行为，（3）数学模型形式欠妥，（4）归并误差（粮食的归并）（5）测量误差等。

回归模型存在两个特点。

（1）建立在某些假定条件不变前提下抽象出来的回归函数不能百分之百地再现所研究的经济过程。

（2）也正是由于这些假定与抽象，才使我们能够透过复杂的经济现象，深刻认识到该经济过程的本质。

通常线性回归函数E(y t) = β0 + β1 x t是观察不到的，利用样本得到的只是对E(y t) = β0 + β1 x t 的估计，即对β0和β1的估计。

在对回归函数进行估计之前应该对随机误差项u t做出如下假定。

(1) u t 是一个随机变量，u t 的取值服从概率分布。

十一章1. 解：回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

回归分析按照涉及的变量的多少，分为一元回归和多元回归分析；在线性回归中，按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且自变量之间存在线性相关，则称为多元线性回归分析。

相关分析，相关分析是研究现象之间是否存在某种依存关系，并对具体有依存关系的现象探讨其相关方向以及相关程度，是研究随机变量之间的相关关系的一种统计方法。

相关分析和回归分析是研究客观现象之间数量联系的重要统计方法。

既可以从描述统计的角度，也可以从推断统计的角度来说明。

所谓相关分析，就是用一个指标来表明现象间相互依存关系的密切程度。

所谓回归分析，就是根据相关关系的具体形态，选择一个合适的数学模型，来近似地表达变量间的平均变化关系。

它们具有共同的研究对象，在具体应用时，相关分析需要依靠回归分析来表明现象数量相关的具体形式，而回归分析则需要依靠相关分析来表明现象数量变化的相关程度。

只有当变量之间存在着高度相关时，进行回归分析寻求其相关的具体形式才有意义。

由于相关分析不能指出变量间相互关系的具体形式，所以回归分析要对具有相关关系的变量之间的数量联系进行测定，从而为估算和预测提供了一个重要的方法。

在有关管理问题的定量分析中，推断统计加具有更加广泛的应用价值。

需要指出的是，相关分析和回归分析只是定量分析的手段。

通过相关与回归分析，虽然可以从数量上反映现象之间的联系形式及其密切程度，但是现象内在联系的判断和因果关系的确定，必须以有关学科的理论为指导，结合专业知识和实际经验进行分析研究，才能正确解决。

因此，在应用时要把定性分析和定量分析结合起来，在定性分析的基础上开展定量分析。

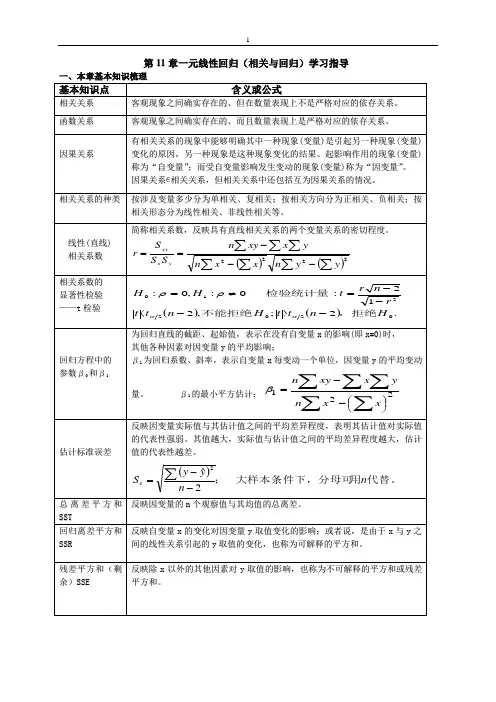
第11章一元线性回归（相关与回归）学习指导一、本章基本知识梳理基本知识点含义或公式相关关系 客观现象之间确实存在的、但在数量表现上不是严格对应的依存关系。

函数关系 客观现象之间确实存在的、而且数量表现上是严格对应的依存关系。

因果关系有相关关系的现象中能够明确其中一种现象(变量)是引起另一种现象(变量)变化的原因，另一种现象是这种现象变化的结果。

起影响作用的现象(变量)称为“自变量”；而受自变量影响发生变动的现象(变量)称为“因变量”。

因果关系∊相关关系，但相关关系中还包括互为因果关系的情况。

相关关系的种类 按涉及变量多少分为单相关、复相关；按相关方向分为正相关、负相关；按相关形态分为线性相关、非线性相关等。

线性(直线) 相关系数 简称相关系数，反映具有直线相关关系的两个变量关系的密切程度。

()()∑∑∑∑∑∑∑---==2222y yn x xn yx xy n SS S r yx xy相关系数的 显著性检验 ——t 检验 ()().2;,212:0:,0:020221Hn t t Hn t t rn r t HH，拒绝不能拒绝检验统计量-〉-〈--=≠=ααρρ回归方程中的 参数β0和β1为回归直线的截距、起始值，表示在没有自变量x 的影响(即x =0)时，其他各种因素对因变量y 的平均影响；β1为回归系数、斜率，表示自变量x 每变动一个单位，因变量y 的平均变动量。

β1的最小平方估计：∑∑∑∑∑⎪⎭⎫ ⎝⎛--=221x x n yx xy nβ估计标准误差反映因变量实际值与其估计值之间的平均差异程度，表明其估计值对实际值的代表性强弱。

其值越大，实际值与估计值之间的平均差异程度越大，估计值的代表性越差。

()代替。

用大样本条件下，分母可；n n yyS e 2ˆ2--=∑总离差平方和S S T反映因变量的n 个观察值与其均值的总离差。

回归离差平方和S S R 反映自变量x 的变化对因变量y 取值变化的影响；或者说，是由于x 与y 之间的线性关系引起的y 取值的变化，也称为可解释的平方和。

第十一章一元线性回归练习题答案二．填空题 1. 不能；因为该相关系数为样本计算出的相关系数，它的大小受样本数据波动的影响，它是否显著尚需检验；t 检验;2.图1；不能；因为图1反映的是线性相关关系，图2反映的是非线性性相关关系，相关系数只能反映线性相关变量间的相关性的强弱，不能反映非线性相关性的强弱。

三．计算题1.（1） SSR 的自由度是1，SSE 的自由度是18。

（2）2418/6080220/1/==-=SSE SSR F(3)判定系数%14.57140802===SST SSR R 在y 的总变差中，由57.14％的变差是由于x 的变动说引起的。

(4)7559.05714.02-=-=-=R r相关系数为-0.7559。

(5)线性关系显著和：线性关系不显著和y x y x H 10H :因为414.424=>=αF F，所以拒绝原假设，x 与y 之间的线性关系显著。

2.（1）方差分析表df SS MS F Significance F回归分析 1 425 425 85 0.017 残差 15 75 5 － － 总计16500－－－（2）判定系数%8585.05004252====SST SSR R表明在维护费用的变差中，有85％的变差可由使用年限来解释。

（3）9220.085.02===R r二者相关系数为0.9220，属于高度相关（4）x y248.1388.6ˆ+= 分布；显著。

的自由度为t n r n r t 2);12||2---=回归系数为1.248，表示每增加一个单位的产量，该行业的生产费用将平均增长1.248个单位。

（5）线性关系显著性检验：线性关系显著：生产费用和产量之间性关系不显著生产费用和产量之间线10:H H因为Significance F=0.017<05.0＝α,所以线性关系显著。

（6）348.3120248.1388.6248.1388.6ˆ＝＝⨯++=x y当产量为10时，生产费用为31.348万元。

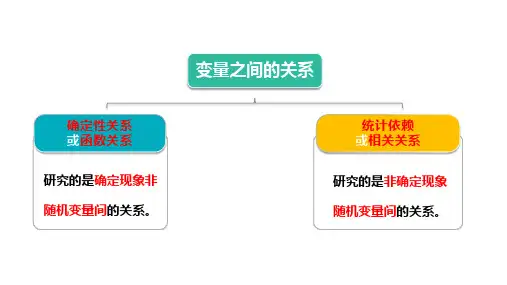
变量之间的关系研究的是确定现象非随机变量间的关系。

确定性关系或函数关系统计依赖或相关关系研究的是非确定现象随机变量间的关系。

例如：函数关系XX f Y 2)(==细胞分裂关系()2,半径半径圆面积⋅==ππf 例如：统计依赖关系/统计相关关系款利率）可支配收入，消费，存城镇居民储蓄(f =),,,(施肥量阳光降雨量气温农作物产量f =相关分析——（两个）变量对称——两者都是随机的回归分析——非对称——应变量（被解释变量、随机）自变量（解释变量、确定）有相关关系、统计依赖关系，不一定有因果关系相关分析与回归分析甘肃江西GDP Y GDP X Y D X D Y X COV XY ====;95.0)()(),(ρ款利率）可支配收入，消费，存城镇居民储蓄(f =无因果关系有因果关系被解释变量解释变量回归分析(regression analysis)是研究一个变量关于另一个（些）变量的具体依赖关系的计算方法和理论。

前者——被解释变量（Explained Variable ）或应变量（Dependent Variable ）。

后者——解释变量（Explanatory Variable ）或自变量（Independent Variable ）。

回归分析的基本概念本课程重要研究方法其用意：通过解释变量，去估计被解释变量的（总体）均值。

回归分析的基本概念价指数）可支配收入，消费，物城镇居民储蓄(f 被解释变量解释变量研究解释变量对被解释变量的影响程度、影响大小及影响方向。

●求得回归方程●显著性检验回归分析内容●分析、评价及预测回归分析内容政策建议总体回归函数例2.1.1：一个假想社区有100户家庭，研究该社区每月家庭消费支出Y与每月家庭可支配收入X的关系。

即：已知家庭月收入，能否预测平均月消费支出？为达到此目的，将该100户家庭划分为组内收入差不多的10组，以分析每一收入组的家庭消费支出。

按收入分组同一收入水平X，消费支出Y不完全相同；给定X的消费Y的条件均值（conditional mean）或条件期望（conditionalexpectation）记为：E(Y|X=Xi) ；随着收入水平X上升，E(Y|X=Xi)逐渐上升；由上表可知E(Y | X=800)=605；E(Y | X=3500)=2585；05001000150020002500300035005001000150020002500300035004000每月可支配收入X （元）每月消费支出Y（元）散点图发现随着收入的增加，消费“平均地说”也在增加，且Y 的条件均值均落在一根正斜率的直线上。

一章1. 解：回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

回归分析按照涉及的变量的多少，分为一元回归和多元回归分析；在线性回归中，按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且自变量之间存在线性相关，则称为多元线性回归分析。

相关分析，相关分析是研究现象之间是否存在某种依存关系，并对具体有依存关系的现象探讨其相关方向以及相关程度，是研究随机变量之间的相关关系的一种统计方法。

相关分析和回归分析是研究客观现象之间数量联系的重要统计方法。

既可以从描述统计的角度，也可以从推断统计的角度来说明。

所谓相关分析，就是用一个指标来表明现象间相互依存关系的密切程度。

所谓回归分析，就是根据相关关系的具体形态，选择一个合适的数学模型，来近似地表达变量间的平均变化关系。

它们具有共同的研究对象，在具体应用时，相关分析需要依靠回归分析来表明现象数量相关的具体形式，而回归分析则需要依靠相关分析来表明现象数量变化的相关程度。

只有当变量之间存在着高度相关时，进行回归分析寻求其相关的具体形式才有意义。

由于相关分析不能指出变量间相互关系的具体形式，所以回归分析要对具有相关关系的变量之间的数量联系进行测定，从而为估算和预测提供了一个重要的方法。

在有关管理问题的定量分析中，推断统计加具有更加广泛的应用价值。

需要指出的是，相关分析和回归分析只是定量分析的手段。

通过相关与回归分析，虽然可以从数量上反映现象之间的联系形式及其密切程度，但是现象内在联系的判断和因果关系的确定，必须以有关学科的理论为指导，结合专业知识和实际经验进行分析研究，才能正确解决。

因此，在应用时要把定性分析和定量分析结合起来，在定性分析的基础上开展定量分析。

第11章一元线性回归一、思考题1．解释相关关系的含义，说明相关关系的特点。

答：变量之间存在的不确定的数量关系，称为相关关系。

相关关系的特点：一个变量的取值不能由另一个变量唯一确定，当变量x取某个值时，变量y的取值可能有几个。

对这种关系不确定的变量是不能用函数关系进行描述的。

2．相关分析主要解决哪些问题？答：相关分析就是对两个变量之间线性关系的描述与度量，它要解决的问题包括：（1）变量之间是否存在关系；（2）如果存在关系，它们之间是什么样的关系；（3）变量之间的关系强度如何；（4）样本所反映的变量之间的关系能否代表总体变量之间的关系。

3．相关分析中有哪些基本假定？答：在进行相关分析时，对总体主要有以下两个假定：（1）两个变量之间是线性关系；（2）两个变量都是随机变量。

4．简述相关系数的性质。

答：相关系数是根据样本数据计算的度量两个变量之间线性关系强度的统计量。

若相关系数是根据总体全部数据计算的，称为总体相关系数，记为ρ；若是根据样本数据计算的，则称为样本相关系数，记为r 。

相关系数的性质：（1）r 的取值范围在－1～＋1之间，即－1≤r ≤1。

若0<r ≤1，表明x 与y 之间存在正线性相关关系；若－1≤r <0，表明x 与y 之间存在负线性相关关系；若r =＋1，表明x 与y 之间为完全正线性相关关系；若r =－1，表明x 与y 之间为完全负线性相关关系。

可见当|r |=1时，y 的取值完全依赖于x ，二者之间即为函数关系；当r ＝0时，说明y 的取值与x 无关，即二者之间不存在线性相关关系。

（2）r 具有对称性。

x 与y 之间的相关系数xy r 和y 与x 之间的相关系数yx r 相等，即xy r =yx r 。

（3）r 数值大小与x 和y 的原点及尺度无关。

改变x 和y 的数据原点及计量尺度，并不改变r 数值大小。

（4）r 仅仅是x 与y 之间线性关系的一个度量，它不能用于描述非线性关系。

一元线性回归公式一元线性回归（SimpleLinearRegression）是一种简单的回归分析方法，用于研究两个定量变量之间的关系。

一元线性回归是指一个定量变量Y和一个自变量X之间的线性回归模型，它有一个参数β，用来表示X对Y的影响程度。

一元线性回归的公式如下：Y =0 +1X其中，β0表示Y的偏移量或均值，是X=0时Y的值；β1表示X对Y的影响程度，是X的系数。

一元线性回归的原理是通过拟合一条线来求解X和Y的关系，并计算出X对Y的影响程度。

通常，我们需要用到两个原则：最小二乘法（Least Squares）和最大似然估计（Maximum Likelihood）。

最小二乘法是一种优化方法，其目标是最小化残差的平方和。

残差是Y实际值与拟合模型计算值的差，残差的平方和就是拟合的均方差（Mean Squared Error，MSE）。

因此，最小二乘法的目标是最小化拟合均方差。

最大似然估计是一种概率模型估计方法，其目标是最大化模型似然函数。

似然函数是模型参数取某一特定值时，样本出现的概率，因此，最大似然估计的目标是最大化似然函数。

一元线性回归公式的应用非常广泛，可用于检测两个变量之间的因果关系，或者对比不同变量对另一变量的影响程度，或者预测变量值。

比如，在多重回归中，可以用一元线性回归来研究某一变量的影响程度；在财务分析中，可以用它来预测股票价格；在销售分析中，可以用它来预测某一产品的销售量；在投资分析中，可以利用它来估计投资回报率；在决策分析中，可以利用它来估计某一政策的收益；以及在其他应用中也可以利用它来预测变量值。

此外，一元线性回归还可以用于检验变量之间的关系，比如，用相关分析来检验两个变量之间的关系或使用显著性检验来检验X对Y 的影响是否有效。

对于一元线性回归而言，可以通过以下步骤来建模：首先，分析变量间的关系，看看X是否和Y有线性关系；其次，计算拟合系数β1和β0；最后，检验拟合模型的精度。

一元线性回归第十一章一元线性回归一、填空题1、对回归系数的显著性检验，通常采用的是检验。

2、若回归方程的判定系数R 2=0.81，则两个变量x 与y 之间的相关系数r 为_________________。

3、若变量x 与y 之间的相关系数r=0.8，则回归方程的判定系数R 2为____________。

4、对于直线趋势方程bx a y c +=，已知∑=,0x ∑=130xy ，n=9，1692=∑x， a=b ，则趋势方程中的b=______。

5、回归直线方程bx a y c +=中的参数b 是_____________。

估计待定参数a 和 b 常用的方法是-_________________。

6、相关系数的取值范围_______________。

7、在回归分析中，描述因变量y 如何依赖于自变量x 和误差项的方程称为。

8、在回归分析中，根据样本数据求出的方程称为。

9、在回归模型εββ++=x y 10中的ε反映的是。

10、在回归分析中，F 检验主要用来检验。

11、说明回归方程拟合优度检验的统计量称为。

二、单选题1、年劳动生产率（x ：千元）和工人工资（y ：元）之间的回归方程为1070y x =+，这意味着年劳动生产率没提高1千元，工人工资平均（）A 、增加70元B 、减少70元C 、增加80元D 、减少80元2、两变量具有线形相关，其相关系数r=-0.9，则两变量之间（）。

B 、弱相关C 、不相关D 、负的弱相关关系 3、变量的线性相关关系为0，表明两变量之间（）。

A 、完全相关B 、无关系C 、不完全相关D 、不存在线性关系4、相关关系与函数关系之间的联系体现在（）。

A 、相关关系普遍存在，函数关系是相关关系的特例 B 、函数关系普遍存在，相关关系是函数关系的特例C 、相关关系与函数关系是两种完全独立的现象D 、相关关系与函数关系没有区别5、已知x 和y 两变量之间存在线形关系，且δx =10, δy =8, δxy2=-7,n=100,则x 和y 存在着（）。