下载文档原格式
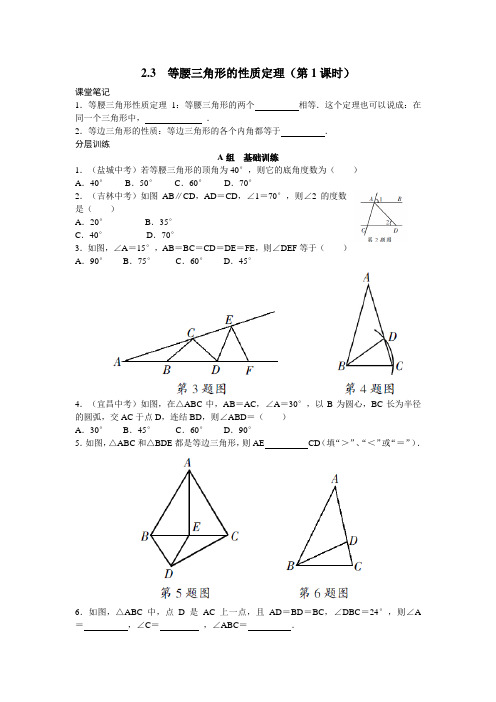
2.3 等腰三角形的性质定理（第1课时）课堂笔记1．等腰三角形性质定理1：等腰三角形的两个相等．这个定理也可以说成：在同一个三角形中，．2．等边三角形的性质：等边三角形的各个内角都等于．分层训练A组基础训练1．（盐城中考）若等腰三角形的顶角为40°，则它的底角度数为（）A．40°B．50°C．60°D．70°2．（吉林中考）如图AB∥CD，AD＝CD，∠1＝70°，则∠2的度数是（）A．20°B．35°C．40°D．70°3．如图，∠A＝15°，AB＝BC＝CD＝DE＝FE，则∠DEF等于（）A．90°B．75°C．60°D．45°4．（宜昌中考）如图，在△ABC中，AB＝AC，∠A＝30°，以B为圆心，BC长为半径的圆弧，交AC于点D，连结BD，则∠ABD＝（）A．30°B．45°C．60°D．90°5．如图，△ABC和△BDE都是等边三角形，则AE CD（填“＞”、“＜”或“＝”）．6．如图，△ABC中，点D是AC上一点，且AD＝BD＝BC，∠DBC＝24°，则∠A ＝，∠C＝，∠ABC＝．7．①在△ABC中，AB＝BC，∠A＝80°，则∠B＝；②若等腰三角形的一个外角为140°，则它的顶角的度数为.8．如图，四边形ABCD是正方形，△PAD是等边三角形，则∠BPC的度数为．9．如图，在△ABC中，∠ACB＝90°，在AC上取点D，使AD＝BD，连结BD，若∠DBC＝20°，求∠A的度数．10．（宿迁中考）如图，已知AB＝AC＝AD，且AD∥BC，求证：∠C＝2∠D.11．如图，在四边形ABCD中，已知AB＝AD，CB＝CD.求证：∠ABC＝∠ADC.B组自主提高12．已知等腰三角形有一个角为40°，则一腰上的高线与另一腰的夹角为（）A．40°B．50°C．10°D．50°或10°13．已知△ABC中，AB＝AC，D是BC上一点，连结AD，若△ACD和△ABD都是等腰三角形，则∠C的度数为.14．如图，△ABC中，点D，E分别在AC，AB上，AB＝AC，BC＝BD，AD＝DE＝EB，求∠A的度数．15．如图，在△ABC 中，已知BC ＝AC ，∠BAC 的外角平分线交BC 的延长线于点D.若∠ADC ＝21∠CAD ，求∠ABC 的度数．C 组 综合运用16．在△ABC 中，AB ＝AC.（1）如图1，若∠BAD ＝30°，AD 是BC 边上的高线，AD ＝AE ，则∠EDC ＝ ．（2）如图2，若∠BAD ＝50°，AD 是BC 边上的高线，AD ＝AE ，则∠EDC ＝ ．（3）通过以上两题可以发现∠BAD 与∠EDC 之间有什么关系？请用式子表示： ．（4）如图3，若AD 不是BC 边上的高线，AD ＝AE ，是否仍有上述关系？如有，请说明理由．答案2.3 等腰三角形的性质定理（第1课时）【课堂笔记】1. 底角 等边对等角2. 60°【分层训练】1—4. DCCB5. ＝6. 39° 78° 63°7. ①20°；②40°或100°8. 30°9. ∠A ＝35°10. ∵AB ＝AC ＝AD ，∴∠C ＝∠ABC ，∠D ＝∠ABD ，∴∠ABC ＝∠CBD ＋∠D. ∵AD ∥BC ，∴∠CBD ＝∠D. ∴∠ABC ＝∠D ＋∠D ＝2∠D. ∴∠C ＝2∠D.11. 连结BD ，∵AB ＝AD （已知），∴∠ABD ＝∠ADB ，又∵CB ＝CD （已知），∴∠CBD ＝∠CDB ，∴∠ABD ＋∠CBD ＝∠ADB ＋∠CDB ，即∠ABC ＝∠ADC.12. D13. 36°或45°14. 设∠ABD ＝x ，则根据题意可得∠BDE ＝x ，∠AED ＝∠A ＝2x ，则∠C ＝∠BDC ＝3x ，所以∠DBC ＝3x －x ＝2x ，所以2x ＋3x ＋3x ＝180°，得x ＝22.5°，则∠A ＝45°.15. 如图，设∠ABC ＝x ，∠CAD ＝y ，则∠ACD ＝2x ，∠ADC ＝21∠CAD ＝21y ，∴x+2y=180°，2x+23y=180°，解得x=36°，y=72°，∴∠ABC ＝36°.16. （1）15° （2）25° （3）∠BAD ＝2∠EDC（4）仍有．理由如下：∵∠ADC 是△ABD 的外角，∴∠EDC ＋∠ADE ＝∠B ＋∠BAD. 同理，∠AED ＝∠C ＋∠EDC. ∵AD ＝AE ，∴∠ADE ＝∠AED. ∵AB ＝AC ，∴∠B ＝∠C ，∴∠EDC ＋∠C ＋∠EDC ＝∠C ＋∠BAD ，∴∠BAD ＝2∠EDC.。
