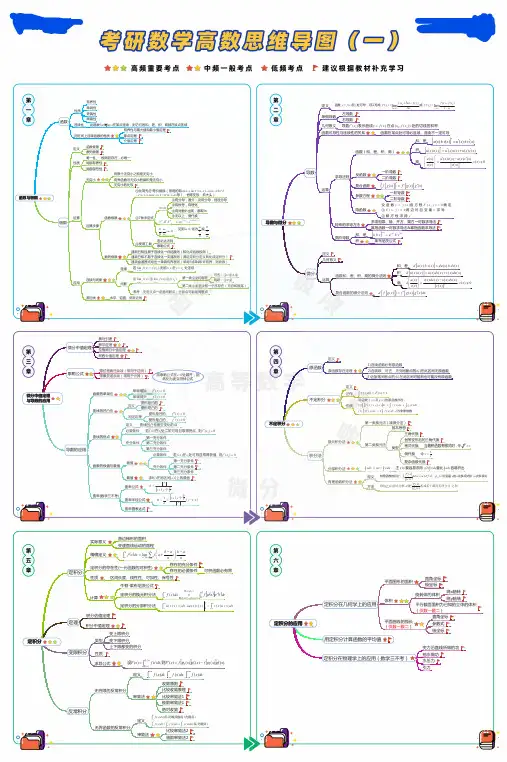
高等数学极限与连续思维导图
- 格式:pdf
- 大小:286.03 KB
- 文档页数:1

高等数学:(11)函数的连续性(第一章极限)
我们生活中有很多关于连续函数的例子,如我们的身高随着时间发生变化的过程,河水的流动,一个物体的运动轨迹等等,今天我们就来学习函数的连续性。
一个连续的函数是可以一笔画到底的,不需要间断,如下图:
函数连续的定义:设函数y=f(X)在点Xo的某一领域内有定义,如果当X→Xo时,f(X)的极限值等于f(Xo), 那么称函数f(X)在点Xo连续。
一般关于函数连续的题目都是给出一个分段函数,告诉我们该函数在某处连续,然后让我们求出分段函数中的未知参数。
我们只需要求出函数在题目给的连续点的极限值,并将极限值与函数在那一点的值建立一个等式,解出未知数。
有时题目还会让我们讨论左右极限的情况,如下例题:
谢谢观看。
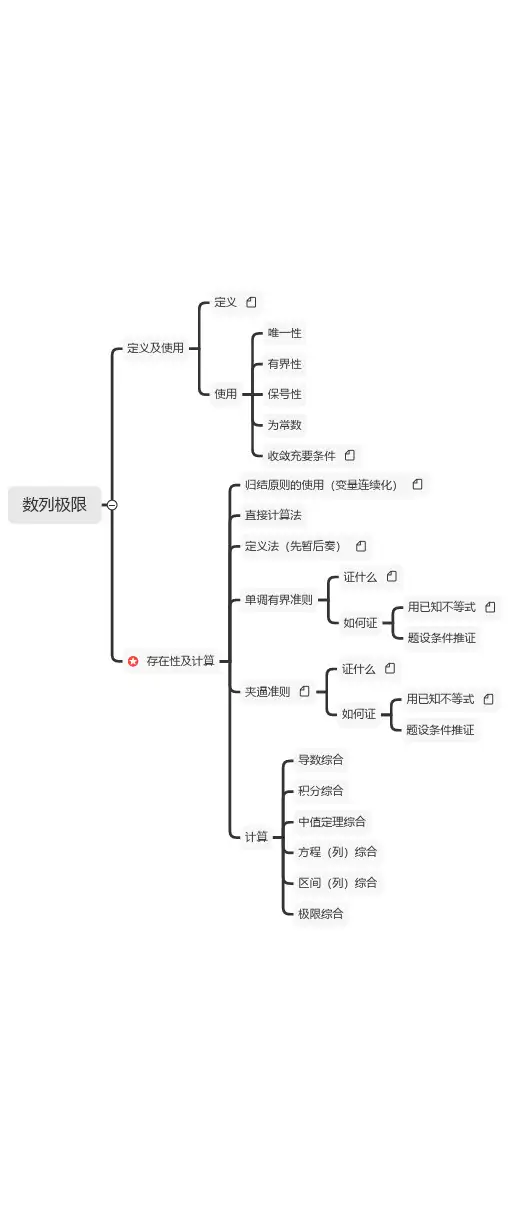


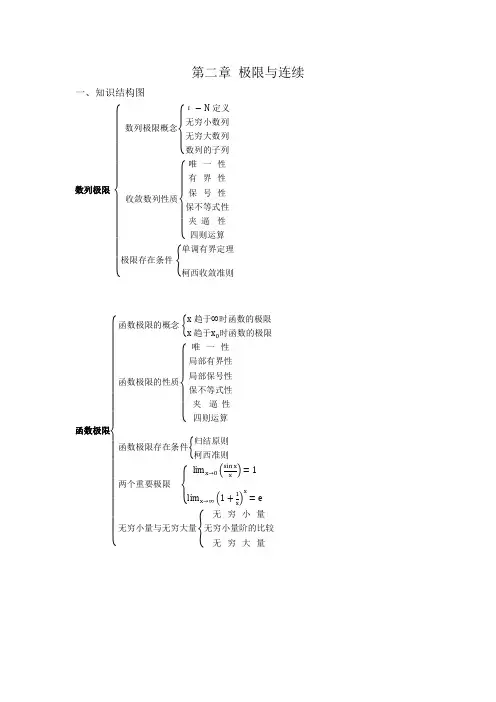

高数大一上知识点思维导图高等数学是大一学生必修的一门课程,因为其抽象性和难度较大,对很多同学来说是一项挑战。
为了更好地掌握高等数学的知识点,提高学习效果,我整理了一份高等数学大一上知识点的思维导图。
下面就让我们一起来看看这份思维导图吧!在高等数学大一上的学习中,主要包含了导数与微分、积分与不定积分、微分方程三个部分。
首先,让我们从导数与微分这一部分开始。
在导数与微分这一部分中,首先介绍了函数与极限的概念。
函数是高等数学的基础,它是自变量和因变量之间的关系。
而极限则是函数无限逼近某一点的过程,通过极限我们可以研究函数在一个点的性质。
接着介绍了导数的概念,导数是函数变化率的度量,表示函数在某一点的瞬时变化率。
在导数的求解中,我们需要掌握一些常用的导数公式和运算法则。
通过这些工具,我们可以求解导数问题,如求函数的导函数、求曲线的切线等。
接下来是积分与不定积分这一部分。
积分是导数的逆运算,表示函数在一定区间内的累积变化量。
不定积分则是求积分的一种方法,其中的不定积分常数表示在不同点处的积分结果可能不同。
在积分与不定积分的学习中,我们需要熟练掌握换元法、分部积分法和定积分的计算。
这些方法可以帮助我们解决一些复杂的积分问题,如求某个函数的原函数、求曲线下的面积等。
最后是微分方程这一部分。
微分方程是含有未知函数及其导数的方程,通过求解微分方程我们可以得到函数的解析表达式。
在微分方程的求解中,我们需要掌握一些基本的解法,如可分离变量法、一阶线性微分方程的求解方法等。
此外,对于高阶微分方程,我们还需要熟悉齐次线性微分方程、非齐次线性微分方程和常系数线性齐次微分方程的特解等的求解方法。
通过这份思维导图,我们可以更好地了解高等数学大一上的知识点,并掌握相关的考点和解题技巧。
但是仅仅依靠思维导图是不够的,我们还需要辅以大量的练习,不断总结和思考,加深对知识点的理解和运用。
总之,高等数学是一门需要思维和逻辑能力的课程,通过合理的学习方法和不懈的努力,我们一定能够掌握好这门课程。


高数大一下知识点思维导图高数是大学数学的一门重要课程,对于大一下学期同学们来说,掌握好高数知识点非常重要。
在这篇文章中,我将为你展示一张思维导图,涵盖了大一下学期高数的重要知识点。
同时,我还将对其中的一些知识点进行解析和讲解,帮助你更好地理解和掌握这些概念。
首先,让我们来看一张思维导图,该导图将大一下学期高数的主要知识点进行了分类和组织。
这样的思维导图有助于我们全面地了解高数的知识结构和框架,让我们更加有条理地学习和应用这些知识。
在这张思维导图中,我将高数的知识点分为四个主要方面:微分与导数、积分与不定积分、微积分应用和级数。
接下来,让我们一起深入了解这些知识点。
首先是微分与导数部分。
微分与导数是高数的核心内容,掌握好这一部分的知识对于学习后续内容非常重要。
在这一部分,我们需要了解函数的定义、连续性、可导性等基本概念,以及求导的基本方法和公式。
特别是常见的导函数公式和高阶导数的计算方法,都需要我们熟练掌握。
除此之外,还要了解导数在图像上的几何意义,比如斜率、切线等概念。
接下来是积分与不定积分部分。
积分是导数的逆运算,学习好积分与不定积分的概念和计算方法可以帮助我们解决各种实际问题。
在这一部分,我们需要掌握不定积分的基本性质和公式,以及一些特殊函数的积分计算方法。
同时,还要了解定积分的概念和性质,理解积分在几何和物理上的应用。
第三部分是微积分应用。
微积分的应用广泛而深入,可以帮助我们解决各种实际问题。
在这一部分,我们需要学习如何应用微积分的知识解决最值问题、曲线绘制、面积和体积计算等数学和物理问题。
同时,还需要了解微积分在经济学、生物学等领域的应用。
最后是级数部分。
级数是由无穷多个数相加或相乘形成的数列或数列的极限。
在这一部分,我们需要掌握级数的概念和性质,了解级数收敛和发散的判别方法,同时还要学习级数求和的一些基本技巧。
以上就是大一下学期高数的主要知识点,通过这张思维导图,我们可以更好地梳理和理解这些知识点。
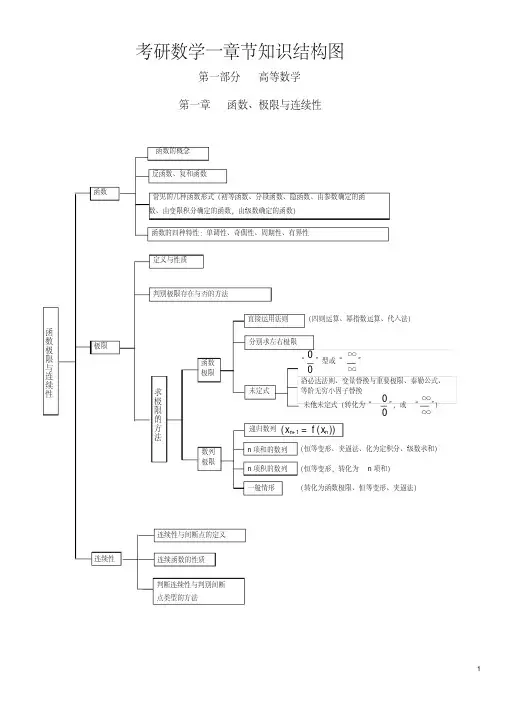
函数的极限、连续极限定义性质唯一性局部有界性局部保号性重要计算方法洛必达法则运算法则泰勒公式公式展开原则1无穷小比阶无穷小量高阶无穷小lim f(x)\g(x)=x→\?02低阶无穷小lim f(x)\g(x)=x→\?∞3等阶无穷小5lim f(x)\g(x)=x→\?14同阶无穷小lim f(x)\g(x)=x→\?A(不包括0,1)6(7个)未定式的样式和已定式的具体解法未定式——0/0I——1^∞II——∞/∞III——∞-∞IV——0*∞V——∞^0VI——0^0VII已定式带入数值直接计算连续、间断连续点的定义间断点的分类第一间断点可去间断点左、右极限存在,并且相同子主题1跳跃间断点左、右极限存在,并且不相同子主题1第二间断点无穷间断点子主题1震荡间断点子主题1备注:1. 适用条件主要原则:相消不为零原则次要原则:上下同阶原则2. 函数f(x)趋向于∞的速度函数g(x)快可以理解为高阶比低阶3. 函数f(x)趋向于∞的速度函数g(x)慢可以理解为低阶比高阶4. 两个函数趋向于1的速度一样快(同阶)5. 适用条件:x趋向于0,?趋向于01、sin x~x ——(推广) sin ?=?2、arc sin x~x ——(推广)arc sin ?~?3、tan x~x ——(推广)tan ?~?4、arc tan x~x ——(推广)arc tan?~? 5、e^x-1~x ——(推广)e^?-1~? 6、ln (1+x)~x ——(推广)l n (1+?)~?7、1- cos x~1\2 x^2 ——(推广)1- cos?~1\2 ?^2 8、(1+x)^?-1~?x ——(推广) (1+?)^a-1~a?6. 两个函数趋向于A的速度差不多一样快(同阶)。