图的搜索算法

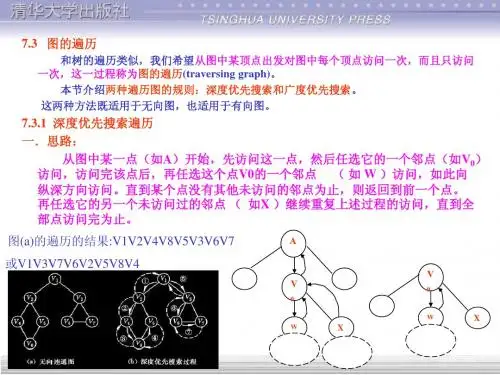
深度优先算法和广度优先算法都是图搜索中常见的算法，它们具有不同的特点和适用场景。

在进行全面评估之前，让我们先来了解一下深度优先算法和广度优先算法的基本概念和原理。

### 1. 深度优先算法（Depth-First Search, DFS）深度优先算法是一种用于遍历或搜索树或图的算法。

其核心思想是从起始顶点出发，沿着一条路径直到末端，然后回溯，继续搜索下一条路径，直到所有路径都被探索。

在实际应用中，深度优先算法常常通过递归或栈来实现。

### 2. 广度优先算法（Breadth-First Search, BFS）广度优先算法也是一种用于遍历或搜索树或图的算法。

其核心思想是从起始顶点出发，依次遍历该顶点的所有相邻顶点，然后再以这些相邻顶点作为起点，继续遍历它们的相邻顶点，以此类推，直到所有顶点都被遍历。

在实际应用中，广度优先算法通常通过队列来实现。

### 3. 深度优先算法和广度优先算法的时间复杂度在实际应用中，我们经常需要对算法的时间复杂度进行分析。

针对深度优先算法和广度优先算法，它们的时间复杂度并不相同。

- 深度优先算法的时间复杂度：O(V + E)，其中V为顶点数，E为边数。

在最坏的情况下，如果采用邻接矩阵来表示图的话，深度优先算法的时间复杂度为O(V^2)；如果采用邻接表来表示图的话，时间复杂度为O(V + E)。

- 广度优先算法的时间复杂度：O(V + E)，其中V为顶点数，E为边数。

无论采用邻接矩阵还是邻接表表示图，广度优先算法的时间复杂度都是O(V + E)。

### 4. 个人理解和观点在实际应用中，我们在选择使用深度优先算法还是广度优先算法时，需要根据具体的问题场景来进行选择。

如果要寻找图中的一条路径，或者判断两个节点之间是否存在路径，通常会选择使用深度优先算法；如果要寻找最短路径或者进行层次遍历，通常会选择使用广度优先算法。

深度优先算法和广度优先算法都是非常重要的图搜索算法，它们各自适用于不同的场景，并且具有不同的时间复杂度。

dfs和bfs算法深度优先搜索（DFS）和广度优先搜索（BFS）是图论中常用的两种搜索算法，也是许多算法题中的基础算法。

本文将从什么是图、什么是搜索算法开始介绍DFS、BFS的基本原理以及应用场景。

一、图的概念图是由节点集合以及它们之间连线所组成的数据结构。

图分为有向图和无向图两种，有向图中的边具有一定的方向性，而无向图中的边是没有方向的。

二、DFS（深度优先搜索）深度优先搜索从一个点开始，根据规定的遍历方式始终向着深度方向搜索下去，直到到达目标节点或者无法继续搜索为止。

具体实现可以用递归或者非递归的方式进行。

1、深度优先搜索的框架def dfs(v,visited,graph):visited[v] = True #将节点v标记为已经被访问#遍历v的所有连接节点for w in graph[v]:if not visited[w]:dfs(w,visited,graph)2、深度优先搜索的应用DFS常用来解决最长路径问题、拓扑排序问题以及判断图是否存在环。

三、BFS（广度优先搜索）广度优先搜索是从一个点开始，逐层扩散的搜索方式。

具体实现可以用队列实现。

1、广度优先搜索的框架def bfs(start,graph):visited = [False] * len(graph) #标记所有节点为未访问queue = [start] #队列存储已经访问过的节点visited[start] = True #起始点被标记为已经访问过while queue:v = queue.pop(0) #弹出队列首节点#遍历该节点的所有连接节点for w in graph[v]:if not visited[w]:visited[w] = True #标记该节点已经被访问queue.append(w) #加入队列2、广度优先搜索的应用BFS常用来解决最短路径问题，如迷宫问题、网络路由问题等。

四、DFS和BFS的区别DFS从一个节点开始，向下深度优先搜索，不断往下搜索直到无路可走才返回，因此将搜索过的节点用栈来存储。

dfs通用步骤-概述说明以及解释1.引言1.1 概述DFS（深度优先搜索）是一种常用的图遍历算法，它通过深度优先的策略来遍历图中的所有节点。

在DFS中，从起始节点开始，一直向下访问直到无法继续为止，然后返回到上一个未完成的节点，继续访问它的下一个未被访问的邻居节点。

这个过程不断重复，直到图中所有的节点都被访问为止。

DFS算法的核心思想是沿着一条路径尽可能深入地搜索，直到无法继续为止。

在搜索过程中，DFS会使用一个栈来保存待访问的节点，以及记录已经访问过的节点。

当访问一个节点时，将其标记为已访问，并将其所有未访问的邻居节点加入到栈中。

然后从栈中取出下一个节点进行访问，重复这个过程直到栈为空。

优点是DFS算法实现起来比较简单，而且在解决一些问题时具有较好的效果。

同时，DFS算法可以用来解决一些经典的问题，比如寻找图中的连通分量、判断图中是否存在环、图的拓扑排序等。

然而，DFS算法也存在一些缺点。

首先，DFS算法不保证找到最优解，有可能陷入局部最优解而无法找到全局最优解。

另外，如果图非常庞大且存在大量的无效节点，DFS可能会陷入无限循环或者无法找到解。

综上所述，DFS是一种常用的图遍历算法，可以用来解决一些问题，但需要注意其局限性和缺点。

在实际应用中，我们需要根据具体问题的特点来选择合适的搜索策略。

在下一部分中，我们将详细介绍DFS算法的通用步骤和要点，以便读者更好地理解和应用该算法。

1.2 文章结构文章结构部分的内容如下所示：文章结构：在本文中，将按照以下顺序介绍DFS（深度优先搜索）通用步骤。

首先，引言部分将概述DFS的基本概念和应用场景。

其次，正文部分将详细解释DFS通用步骤的两个要点。

最后，结论部分将总结本文的主要内容并展望未来DFS的发展趋势。

通过这样的结构安排，读者可以清晰地了解到DFS算法的基本原理和它在实际问题中的应用。

接下来，让我们开始正文的介绍。

1.3 目的目的部分的内容可以包括对DFS（Depth First Search，深度优先搜索）的应用和重要性进行介绍。

深度优先搜索算法（DFS）是一种常用的图算法，该算法主要用于解决有解路径或遍历某个图结构的问题。

的主要思路是从某个图的起始点出发,访问邻居节点，直到该节点没有未被访问的邻居节点为止，然后回溯到上一个节点继续遍历其他未被访问的邻居节点。

该算法的基本流程可以概括为以下几个步骤：1. 从某个图结构的起始点开始进行深度优先搜索。

2. 如果该节点没有未被访问的邻居节点，则回溯到上一个节点。

3. 继续遍历其他未被访问的邻居节点，直到所有的节点已被访问。

4. 搜索结束。

的实现可以使用递归或栈数据结构进行。

使用递归实现时，程序会自动保存每个节点的访问状态，无需手动进行处理。

使用栈数据结构实现时，需要手动保存每个节点的访问状态，以便在回溯时继续遍历其他未被访问的邻居节点。

主要应用于解决以下问题：1. 找出两点之间的最短路径可以用来查找两个节点之间的最短路径。

在进行深度优先搜索时，需要记录每个节点的前驱节点，以便在搜索结束后构造最短路径。

2. 遍历一张图结构可以用来遍历一张图结构。

在进行深度优先搜索时，可以将图中的所有节点都进行遍历。

3. 解决迷宫问题可以用来解决迷宫问题。

在进行深度优先搜索时，需要记录每个走过的位置，以便在搜索结束后构造出从起点到终点的路径。

4. 生成所有排列或组合可以用来生成所有排列或组合。

在进行深度优先搜索时，需要记录已经访问过的节点，以便在搜索结束后生成所有满足条件的排列或组合。

存在一些问题，例如搜索过程中容易陷入死循环、需要记录每个节点的访问状态等。

为了解决这些问题，可以使用剪枝、双向搜索等技术来优化搜索算法。

总之，是一种常用的图算法，该算法主要用于解决有解路径或遍历某个图结构的问题。

的主要思路是从某个图的起始点出发, 访问邻居节点，直到该节点没有未被访问的邻居节点为止，然后回溯到上一个节点继续遍历其他未被访问的邻居节点。

在实际应用中，可以用来查找两个节点之间的最短路径、遍历一张图结构、解决迷宫问题、生成所有排列或组合等。

路径规划与图搜索算法路径规划是指在给定的地图或者网络中，根据一定的条件和优化目标，确定从起点到终点的最佳路径的过程。

在现实生活中，路径规划被广泛应用于交通导航、物流配送、机器人导航等领域。

而图搜索算法是实现路径规划的核心方法之一，本文将介绍路径规划的相关概念和常用的图搜索算法。

一、路径规划的概念路径规划是指通过构建问题的可行解空间，根据一定的约束条件和优化目标，确定从起点到终点的最佳路径。

在路径规划中，可行解空间可用图模型来表示，起点和终点分别为图上的两个节点，路径则是连接起点和终点的一系列边构成的序列。

二、图搜索算法的基本原理图搜索算法是一类基于图模型的搜索算法，其基本原理是通过遍历问题的可行解空间中的节点和边，依次扩展搜索范围，直到找到终点或者达到终止条件为止。

常用的图搜索算法包括深度优先搜索（DFS）、广度优先搜索（BFS）、Dijkstra算法、A*算法等。

1. 深度优先搜索（DFS）深度优先搜索是一种沿着图的深度遍历的搜索算法。

其基本思想是从起点开始，选择一个未被访问的邻接节点，继续向下搜索直到无法继续为止，然后回溯到上一个节点，选择未被访问的其他邻接节点，继续搜索，直到找到终点为止。

2. 广度优先搜索（BFS）广度优先搜索是一种沿着图的广度遍历的搜索算法。

其基本思想是从起点开始，依次访问起点的所有邻接节点，然后再依次访问这些节点的邻接节点，以此类推，直到找到终点为止。

广度优先搜索可以保证找到的路径是最短路径。

3. Dijkstra算法Dijkstra算法是一种用于计算带权图中单源最短路径的贪心算法。

其基本思想是从起点开始，依次选择与当前节点距离最短的邻接节点，并更新最短距离和最短路径，直到找到终点或者所有节点都被访问完为止。

4. A*算法A*算法是一种启发式搜索算法，主要用于解决带权图中的最短路径问题。

其基本思想是综合利用从起点到当前节点的实际距离和当前节点到终点的估计距离，选择综合距离最小的节点进行搜索，直到找到终点为止。

图片搜索原理图片搜索是一种通过图像内容来检索相关信息的技术。

它可以帮助用户在海量的图片库中快速找到所需的图片，也可以用于识别图片中的物体、场景等内容。

图片搜索的原理涉及到图像特征提取、相似度匹配、深度学习等多个方面的知识。

本文将从这些方面对图片搜索的原理进行介绍。

首先，图像特征提取是图片搜索的关键步骤之一。

在图像搜索中，图像特征可以理解为图像的一种描述，它可以用来表示图像的颜色、纹理、形状等特征。

常用的图像特征提取算法包括SIFT（尺度不变特征变换）、SURF（加速稳健特征）、HOG（方向梯度直方图）等。

这些算法可以提取出图像中的关键点、边缘、纹理等特征，为后续的相似度匹配提供了基础。

其次，相似度匹配是图片搜索的核心技术之一。

在图像搜索中，相似度匹配的目标是找到与查询图片最相似的图片。

相似度匹配的方法有很多种，其中最常用的是基于特征的匹配方法，如基于颜色直方图的匹配、基于形状的匹配、基于深度学习的匹配等。

这些方法可以通过计算图像之间的相似度来找到最相似的图片，从而实现图片搜索的功能。

另外，深度学习在图片搜索中也发挥着重要作用。

深度学习是一种通过神经网络来学习图像特征的方法，它可以自动地学习到图像中的高级特征，如边缘、纹理、形状等。

在图片搜索中，深度学习可以帮助我们更准确地提取图像特征，并且可以通过大规模数据的学习来提高搜索的准确性和效率。

总的来说，图片搜索的原理涉及到图像特征提取、相似度匹配、深度学习等多个方面的知识。

通过这些技术的应用，我们可以实现在海量图片库中快速准确地搜索到所需的图片。

随着图像识别技术的不断发展，图片搜索的准确性和效率也会不断提高，为用户提供更好的搜索体验。