[如何画位似图形] 位似图形的画法及步骤

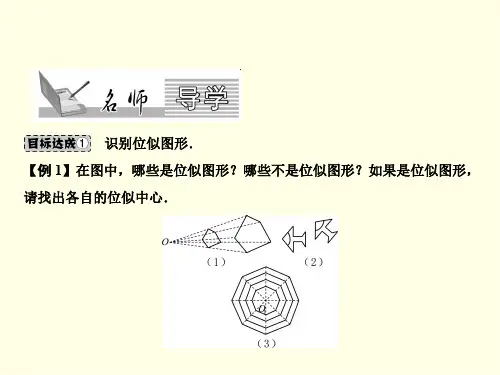
教你画位似图形位似图形是特殊的相似图形，而位似图形的画法要比相似图形的画法容易，因此，相似多边形的画法通常是通过画位似多边形来进行替代下面以四边形为例进行说明例已知四边形ABCD，画四边形A′B′C′D′∽四边形ABCD，且相似比为（>1）方法一：位似中心在图形内部如图1所示，（1）在四边形ABCD内部任取一点O；（2）以点O为端点分别作射线OA、OB、OC、OD；（3）分别在射线OA、OB、OC、OD上取点A′、B′、C′、D′，使OA′∶OA＝OB′∶OB＝OC′∶OC＝OD′∶OD＝（>1）；（4）连接A′B′、B′C′、C′D′、D′A′则四边形A′B′C′D′即为所求作的四边形方法二：位似中心在图形外部如图2所示，（1）在四边形ABCD外部任取一点O；（2）连接OA、OB、OC、OD；（3）分别在OA、OB、OC、OD的反向延长线上取点A′、B ′、C ′、D ′，使OA′∶OA＝OB′∶OB＝OC′∶OC＝OD′∶OD＝（>1）；（4）连接A′B′、B′C′、C′D′、D′A′则四边形A′B′C′D′即为所求作的四边形方法三：位似中心在图形的一边上如图3所示，（1）在四边形ABCD的边AB上任取一点O；（2）分别延长OA、OB，连接OC、OD并延长；（3）分别在OA、OB、OC、OD的延长线上取点A′、B′、C′、D′使OA′∶OA＝OB′∶OB＝OC′∶OC＝OD′∶OD＝（>1）；（4）连接B′C′、C′D′、D′A′则四边形A′B′C′D′即为所求作的四边形小结：综上所述，已知一个图形，画它的位似图形关键有两点：第一，确定位似中心；第二，确定位似比（即相似比）若题中没有明确规定，则可以自由确定，其中位似中心可以是随意的点，位似比可以选择一个适当的数；若题中有限制条件，则根据要求进行，在确定位似比时，要注意的是已知原图与新图的相似比，还是已知新图与原图的相似比，以确定是将原图放大还是缩小跟踪训练如图所示，请你作一个与△ABC位似的缩小图形△A′B′C′，使△A′B′C′与△ABC的位似比为1∶2答案作图略。

[如何画位似图形] 位似图形的画法及步骤[如何画位似图形] 位似图形的画法及步骤如何画位似图形位似变换是新课程标准中涉及的一个重要知识点，它是图形变换的一种，实际上它是相似变换的一种特殊情形，存在位似中心———即对应顶点连线的交点．其位似比就是相似比．作为一个新的知识点，越来越受到中考命题者的青睐．图形放大、缩小通常用位似变换的思想作图，位似中心的位置可在图形顶点处、图形边上、图形内部、图形外部．本文以一道中考题为例介绍几种常见画法，供同学们参考．（辽宁省锦州中考题）如图1，己知四边形ABCD ，用尺规将它放大，使放大前后的图形对应线段的比为1:2．画法一：延长AD 到D 1，使DD 1=AD ，延长AC 到点C 1，使CC 1=AC ，延长AB 到点B 1，使BB 1=AB ，连接D 1C 1，C 1B 1，则四边形A 1B 1C 1D 1即为所求（如图2）．说明：延长AD 得到D 1后，也可以过点D 1作DC 11∥DC ，交AC 的延长线于C 1，再过点C 1作B 1C 1∥BC ，交AC 的延长线于B 1，得到四边形A 1B 1C 1D 1．画法二：延长DA 到点D 1，使A D 1=A 2D ，延长CA 到点C 1，使A C 1=A 2C ，延长BA 到点B 1，使AB 1=2AB 连接B 1C 1，C 1D 1，则四边形A 1B 1C 1D 1即为所求（如图3）．画法三：OB 并延长到点B 1，使任取一点O ，连接OA 并延长到点A 1，使AA 1=OA ，连接BB 1=OB 、连接OC 并延长到点C 1，使CC 1=OC ，连接OD 并延长到点D 1，使，顺次连接A 1B 1，B 1C 1，C 1D 1，D 1A 1，则四边形A 1B 1C 1D 1即为所求（如图4）． DD 1=OD运用这些作图方法可以解决不少数学问题．现举例说明：例如图5，在给定的锐角△ABC 中，求作一个正方形DEFG ，使D ，E 落在BC 上，F ，G 分别落在AC ，AB 边上，要求写出画法．画法：第一步：画一个有三个顶点落在△ABC 两边上的正方形D "E "F "G "（如图5）；第二步：连接BF "并延长交AC 于点F ；第三步：过F 点作FE ⊥BC ，垂足为点E ；第四步：过F 作FG ∥BC 交AB 于点G ；第五步：过G 作GD ⊥BC ，垂足为点D ．四边形DEFG 即为所求的正方形．（如图5）想一想：为什么四边形DEFG 是正方形？请读者思考．。