仰角、俯角++方位角

方位角和俯仰角的定义方位角和俯仰角是天文学和航海学中常用的两个概念，它们在测量和导航中具有重要的意义。

方位角和俯仰角分别用于描述天体或目标的水平方向和垂直方向的位置，这两个参数相互配合可以准确地确定目标的位置和方向。

首先，方位角是指目标相对于参考点的水平方向角度。

通常来说，参考点是指观察者所在的位置，也可以是导航设备上设定的目标位置。

方位角的测量通常是以北方为参照，顺时针方向称为东方，逆时针方向称为西方，这样可以将角度限制在0到360度之间。

方位角的测量可以通过使用罗盘或方位仪等导航设备来完成。

方位角的准确测量对于导航和定位非常重要，例如在航海中确定船只与陆地或其他船只之间的相对位置。

另外，俯仰角是指目标相对于水平面的垂直方向角度。

俯仰角通常用于描述天空中的天体，例如太阳、月亮和星星等。

俯仰角的测量从水平面开始，向上垂直方向为正值，向下为负值。

俯仰角的测量可以通过天文仪器如望远镜或者倾斜传感器等来完成。

在航天、航空等领域，俯仰角的准确测量对于目标的追踪和导航非常重要。

方位角和俯仰角在实际应用中有着广泛的应用。

在天文学中，方位角和俯仰角可以用于确定星体的位置，帮助天文学家观测和研究星体的运动和特性。

在航空航天领域，方位角和俯仰角可以用于飞行器的导航和自动控制系统，实现准确和安全的飞行。

在地理测量和地图制作中，方位角和俯仰角可以用于确定地点之间的方向和相对位置，帮助人们进行定位和导航。

为了准确地测量方位角和俯仰角，在实际操作中我们需要注意一些要点。

首先，需要选择合适的参照点和参考面，确保测量的准确性和一致性。

其次，需要使用精准的仪器和测量方法，避免误差和偏差的积累。

最后，要根据具体的应用需求和情境，选择合适的坐标系统和单位，使测量结果更易于理解和应用。

总而言之，方位角和俯仰角是描述目标水平和垂直方向位置的重要参数。

它们在天文学、航海学和导航等领域有着广泛的应用。

在实际应用中，准确测量和理解方位角和俯仰角对于定位和导航至关重要。

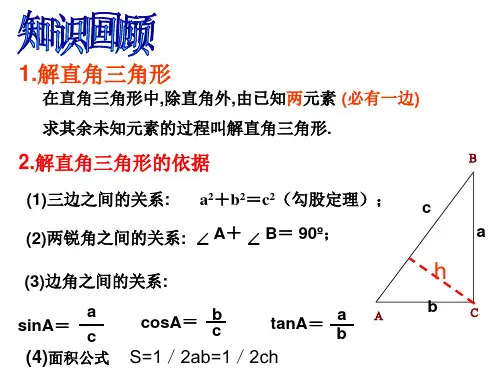
:i h l=hlα基础知识2解直角三角形的应用举例1.仰角与俯角：仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

2.坡度与坡角：坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。

用字母i 表示，即hi l=。

坡度一般写成1:m 的形式，如1:5i =等. 把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα== 3.方位角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方位角.如图,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）.【题型1】仰角与俯角如图，两幢建筑物AB 和CD ，AB ⊥BD ，CD ⊥BD ，AB ＝15m ，CD ＝20m ，AB 和CD 之间有一观景池，小南在A 点测得池中喷泉处E 点的俯角为42°，在C 点测得E 点的俯角为45°（点B 、E 、D 在同一直线上），求两幢建筑物之间的距离BD （结果精确到0.1m ）.（参考数据：sin 42°≈0.67，cos 42°≈0.74，tan 42°≈0.90）【变式训练】1.如图,宁宁在家里楼顶上的点A处，测量建在与自家楼房同一水平线上相邻的电梯楼的高，在点A处看电梯楼顶部点B处的仰角为60°，在点A处看这栋电梯楼底部点C处的俯角为45°，两栋楼之间的距离为30m，则电梯楼的高BC为多少米（精确到0.1）.2.如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）.（参考数据：≈1.414，≈1.732）3.如图，热气球的探测器显示，从热气球A看一栋大楼顶部B的俯角为30°，看这栋大楼底部C的俯角为60°，热气球A的高度为240米，求这栋大楼的高度．4.如图，曦曦在M处用高1米(DM＝1米)的测角仪测得旗杆AB的顶端B的仰角为30°，再向旗杆方向前进10米到F处，又测得旗杆顶端B的仰角为60°，请求出旗杆AB的高度．【题型2】坡度与坡角如图，某水库堤坝横断面迎水坡AB的坡比是1，堤坝高BC=50m，则应水坡面AB的长度是多少？【变式训练】1.如图，在坡度为1∶2的山坡上种树，要求株距(相邻两树间的水平距离)是6米，斜坡上相邻两树间的坡面距离是多少米？2.如图，为了缓解交通拥堵，方便行人，在某街道计划修建一座横断面为梯形ABCD的过街天桥，若天桥斜坡AB的坡角∠BAD为35°，斜坡CD的坡度为i＝1∶1.2(垂直高度CE与水平宽度DE的比)，上底BC＝10 m，天桥高度CE＝5 m，求天桥下底AD的长度．(结果精确到0.1 m，参考数据：sin35°≈ 0.57，cos35°≈ 0.82，tan35°≈ 0.70)3.如图，一楼房AB后有一假山，其坡度为i＝1∶3，山坡坡面上E点处有一休息亭，测得假山坡脚C与楼房水平距离BC＝25米，与亭子距离CE＝20米，小丽从楼房顶测得E点的俯角为45°，求楼房AB的高．(注：坡度i是指坡面的铅直高度与水平宽度的比).4.如图，曦曦在山坡坡脚A 处测得电视塔尖点C 的仰角为60° ，沿山坡向上走到P 处再测得点C 的仰角为45° ，已知OA=100米，山坡坡度为i=1:2， 且O 、A 、B 在同一条直线上。

方位角和俯仰角的取值范围
方位角和俯仰角是空间中位置和方向的两个重要参数。

方位角指
的是某一点相对于某一基准点的方向角度，通常用度数表示，数值范
围为0-360度。

在天文学中，方位角指的是某一恒星相对于地球观测
者的方向角度。

例如，在北半球，北极点的方位角为0度，东方的方
位角为90度，南方的方位角为180度，西方的方位角为270度。

俯仰角是指某一点或某一物体相对于水平面的仰角或俯角。

在天
文学中，俯仰角通常指的是天空中某一恒星或行星相对于地平线的仰
角或俯角。

俯仰角一般用度数表示，其数值范围为-90度到90度。

例如，在北半球观测到的天空中，天顶的俯仰角为90度，地平线的俯仰
角为0度，而南方的天空中某一星座的俯仰角则需要具体情况具体分析。

方位角和俯仰角的测量是天文学研究和定位的重要工具。

通过测
量一个天体的方位角和俯仰角，就可以确定其在天空中的位置。

同时，方位角和俯仰角也被广泛应用于导航、航空、地质、军事等领域。

在
实际使用过程中，为了避免混淆，通常将方位角和俯仰角分别用不同
的符号表示，例如方位角用“Az”表示，俯仰角用“Alt”表示。

这样
就方便人们在探索和研究天文学、地质学、军事等领域时更有效地使
用这些参数。

方位角和俯仰角的取值范围方位角和俯仰角是天文学中常用的两个角度参数，用于描述天体在天空中的位置。

方位角指的是天体相对于北极点的方向角度，俯仰角则是天体相对于地平面的高度角度。

在天文观测中，方位角和俯仰角的取值范围对于观测的准确性和有效性具有重要意义。

方位角的取值范围通常是0°到360°之间，以北极点为基准，顺时针方向为正。

北极点的方位角为0°，东方为90°，南方为180°，西方为270°。

在实际观测中，方位角的取值范围可以根据观测场地的位置和观测目标的运动轨迹进行调整。

例如，在地球表面观测行星运动时，方位角的取值范围会随着行星的位置和运动方向而变化。

俯仰角的取值范围通常是0°到90°之间，以地平面为基准，垂直于地面为正。

观测目标的俯仰角越高，其在天空中的位置就越高。

在实际观测中，俯仰角的取值范围也会随着观测场地的位置和观测目标的高度而变化。

例如，在赤道地区观测天体时，俯仰角的取值范围可以达到90°，而在北极地区观测时则可能只有20°左右。

方位角和俯仰角的取值范围对于天文观测的准确性和有效性具有重要意义。

首先，正确设置方位角和俯仰角的取值范围可以确保观测目标在天空中的位置被准确地确定和记录。

其次，合理地设置方位角和俯仰角的取值范围可以提高观测的效率和准确性，避免观测误差和重复观测的浪费。

最后，方位角和俯仰角的取值范围还可以帮助天文学家更好地理解天体在天空中的运动规律和变化趋势，为天文学研究提供更加准确和全面的数据支持。

综上所述，方位角和俯仰角是天文学中常用的两个角度参数，其取值范围对于天文观测的准确性和有效性具有重要意义。

正确设置方位角和俯仰角的取值范围可以确保观测结果的准确性和完整性，为天文学研究提供重要的数据支持。

方位角和俯仰角的定义
方位角和俯仰角是天文学中常用的两个概念，用来描述天体在观测者视线方向上的位置。

方位角描述了天体与观测者的连线与北方向的夹角，而俯仰角则描述了天体相对于观测者视线的高度角。

方位角通常以度数来表示，从0度开始逆时针旋转，一直到360度。

当方位角为0度时，表示天体位于正北方向；90度表示东方；180度表示正南方；270度表示西方。

方位角的计算可以借助罗盘或者通过天体在天球上的坐标计算得到。

而俯仰角则表示了观测者视线与天体间的垂直夹角。

当俯仰角为0度时，表示天体位于观测者正上方；90度则表示天体在地平线上；当俯仰角超过90度时，表示天体在地平线以下。

掌握方位角和俯仰角的概念对于天文观测是至关重要的。

在进行天体观测时，观测者需要准确地确定天体在视线方向上的位置，才能精确测量其位置和运动。

方位角和俯仰角的测量也是天文仪器设计和编程的基础，帮助观测者确定观测目标的位置和朝向。

在实际观测中，观测者通常会使用专业的天文仪器来测量方位角和俯仰角。

例如，望远镜、天文定位仪等设备可以测量出星体在天球上的坐标，然后根据观测者所处地理位置，计算出相应的方位角和俯仰角。

除了天文观测，方位角和俯仰角的概念也在其他领域有所应用。

例如，无人机、导航系统、航空航天等领域都需要确定目标的方位角和俯仰角，以便准确控制和引导。

总结来说，方位角和俯仰角是天文学中用于描述天体位置的重要概念。

准确测量方位角和俯仰角对于天文观测和其他领域的定位和导航都是至关重要的。

学习和掌握方位角和俯仰角的概念将有助于我们更好地理解天文现象，并在实践中应用这些知识。