仰角、俯角 方位角概要

九年级下册数学仰角和俯角知识点九年级下册数学知识点: 仰角和俯角在九年级的数学学习中，仰角和俯角是两个重要的概念。

仰角和俯角是与水平线之间的夹角，用于描述物体在垂直方向上的视角。

在日常生活中，我们经常会用到仰角和俯角的概念，比如测量高楼的高度、确定飞机的飞行高度等等。

接下来，让我们深入了解仰角和俯角吧。

一、仰角和俯角的定义仰角和俯角是与水平线之间的夹角，用来描述物体在垂直方向上的视角。

仰角是指从水平线向上看时，视线与水平线之间的夹角；俯角则相反，是指从水平线向下看时，视线与水平线之间的夹角。

例如，当我们仰望一棵树时，我们所看到的视线与水平线之间的夹角就是仰角；而当我们低头俯视地面时，视线与水平线之间的夹角就是俯角。

二、仰角和俯角的计算方法我们可以通过三角函数来计算仰角和俯角的数值。

一般来说，我们会用正切函数来求取夹角的数值。

例如，假设一架飞机在空中低飞，飞机和地面之间的夹角为35度。

我们可以通过计算正切函数来求得仰角（从地面向上看时的夹角）和俯角（从飞机向下看时的夹角）的数值。

正切函数的公式为：tanθ = 对边 ÷邻边在这个例子中，飞机和地面之间的夹角为35度，我们可以假设对边（飞机在地面上的高度）为x，邻边（飞机离开地面的水平距离）为1。

代入公式，我们就可以求得正切值。

通过反函数，我们可以得到对应夹角的数值，也就是仰角和俯角。

三、仰角和俯角的应用仰角和俯角的应用非常广泛。

比如在航空领域，飞行员需要准确测量飞机与地面之间的仰角或俯角来确保飞行的安全。

而在建筑领域，工程师需要计算仰角和俯角来确定大楼的高度和斜坡的陡峭程度。

此外，仰角和俯角也在数学的几何和三角学中有着重要的应用。

它们是理解和计算立体图形、三角形、锥体等形状的关键概念之一。

四、总结仰角和俯角是九年级下册数学中的重要知识点。

通过了解仰角和俯角的定义、计算方法和应用，我们可以更好地理解和运用这一概念。

无论是在生活中还是学习中，仰角和俯角都有着广泛的应用价值。

仰角和俯角的意思仰角和俯角是物理学中常用的概念，用于描述物体或光线与地平面的夹角。

在空间导航、航空航天、地理测量等领域中，仰角和俯角的应用非常广泛。

本文将详细介绍仰角和俯角的概念、计算方法及实际应用。

1. 仰角仰角是指物体或者观测点朝天空方向偏离地面的角度，通常用竖直线与视线的夹角来表示。

在天文学中，仰角通常用于描述天体在天空中的位置。

在观测卫星时，需要知道卫星的仰角，以便调整观测仪器的朝向和位置。

2. 俯角二、仰角和俯角的计算方法1. 计算方法（1）在地理测量中，仰角和俯角可以通过测量两点之间的水平距离和垂直距离来计算。

假设A点比B点高h米，则A点到B点的俯角为atan(h/d)，其中d为A点到B点的水平距离。

如果B点比A点高，则仰角为90度减去俯角。

（2）在天文学中，仰角可以通过观测天体时测量天顶角（垂直于地面的角度）和天体高度角（天体与地平面的夹角）来计算。

仰角=90度-天体高度角。

俯角=天体高度角。

（3）在航空航天领域中，仰角和俯角需要通过仪器进行测量。

无人机上装有摄像头，可以通过调整仰角和俯角来改变拍摄视角。

2. 测量仪器（1）测距仪：可以测量两点之间的水平距离和垂直距离。

（2）全站仪：可测量目标物体的仰角、方位角和距离等参数。

三、仰角和俯角的实际应用1. 航空航天在航空航天中，仰角和俯角的应用非常广泛。

飞机、无人机等航空器需要根据目标物体的仰角和俯角来选择飞行高度，调整拍摄角度等。

在航天探测中，也需要测量行星、卫星等目标物体的仰角和俯角。

在地理测量中，仰角和俯角用于计算两点之间的高度差，确定地形高低等。

地面的地形特征对于城市规划、农业种植等方面有着重要的参考价值。

3. 天文观测在天文观测中，仰角和俯角通常用于描述恒星、行星等天体在天空中的位置。

天文观测对于了解宇宙的物理特性和演化历史具有重要的意义。

四、小结仰角和俯角是物理学中重要的概念，在导航、航空航天、地理测量等领域有着广泛的应用。

方位角和俯仰角的定义方位角和俯仰角是天文学和航海学中常用的两个概念，它们在测量和导航中具有重要的意义。

方位角和俯仰角分别用于描述天体或目标的水平方向和垂直方向的位置，这两个参数相互配合可以准确地确定目标的位置和方向。

首先，方位角是指目标相对于参考点的水平方向角度。

通常来说，参考点是指观察者所在的位置，也可以是导航设备上设定的目标位置。

方位角的测量通常是以北方为参照，顺时针方向称为东方，逆时针方向称为西方，这样可以将角度限制在0到360度之间。

方位角的测量可以通过使用罗盘或方位仪等导航设备来完成。

方位角的准确测量对于导航和定位非常重要，例如在航海中确定船只与陆地或其他船只之间的相对位置。

另外，俯仰角是指目标相对于水平面的垂直方向角度。

俯仰角通常用于描述天空中的天体，例如太阳、月亮和星星等。

俯仰角的测量从水平面开始，向上垂直方向为正值，向下为负值。

俯仰角的测量可以通过天文仪器如望远镜或者倾斜传感器等来完成。

在航天、航空等领域，俯仰角的准确测量对于目标的追踪和导航非常重要。

方位角和俯仰角在实际应用中有着广泛的应用。

在天文学中，方位角和俯仰角可以用于确定星体的位置，帮助天文学家观测和研究星体的运动和特性。

在航空航天领域，方位角和俯仰角可以用于飞行器的导航和自动控制系统，实现准确和安全的飞行。

在地理测量和地图制作中，方位角和俯仰角可以用于确定地点之间的方向和相对位置，帮助人们进行定位和导航。

为了准确地测量方位角和俯仰角，在实际操作中我们需要注意一些要点。

首先，需要选择合适的参照点和参考面，确保测量的准确性和一致性。

其次，需要使用精准的仪器和测量方法，避免误差和偏差的积累。

最后，要根据具体的应用需求和情境，选择合适的坐标系统和单位，使测量结果更易于理解和应用。

总而言之，方位角和俯仰角是描述目标水平和垂直方向位置的重要参数。

它们在天文学、航海学和导航等领域有着广泛的应用。

在实际应用中，准确测量和理解方位角和俯仰角对于定位和导航至关重要。

专题1.11解直角三角形（2）——仰角与俯角、方位角、坡角（比）问题（知识讲解）【学习目标】1.理解用三角函数解决实际问题的有关概念；2.理解并解决实际问题中转化为三角函数模型解决实际问题。

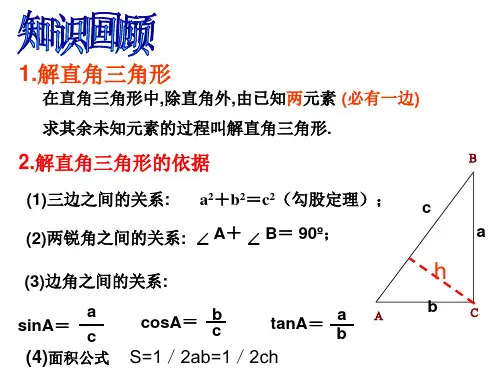
【要点梳理】解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是：(1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.拓展：在用直角三角形知识解决实际问题时，经常会用到以下概念：(1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.坡度(坡比)：坡面的铅直高度h和水平距离的比叫做坡度，用字母表示，则，如图，坡度通常写成=∶的形式.(2)仰角、俯角：视线与水平线所成的角中，视线中水平线上方的叫做仰角，在水平线下方的叫做俯角，如图.(3)方位角：从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角，如图①中，目标方向PA，PB，PC的方位角分别为是40°，135°，245°.(4)方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角，如图②中的目标方向线OA，OB，OC，OD 的方向角分别表示北偏东30°，南偏东45°，南偏西80°，北偏西60°.特别如：东南方向指的是南偏东45°，东北方向指的是北偏东45°，西南方向指的是南偏西45°，西北方向指的是北偏西45°.特别说明：1．解直角三角形实际是用三角知识，通过数值计算，去求出图形中的某些边的长或角的大小，最好画出它的示意图.2．非直接解直角三角形的问题，要观察图形特点，恰当引辅助线，使其转化为直角三角形或矩形来解.3．解直角三角形的应用题时，首先弄清题意(关键弄清其中名词术语的意义)，然后正确画出示意图，进而根据条件选择合适的方法求解.【典型例题】类型一、解直角三角形的应用——仰角和俯角问题1．在一次综合实践活动中，某小组对一建筑物进行测量．如图，在山坡坡脚C处测得该建筑物顶端B 的仰角为60°，沿山坡向上走20m 到达D 处，测得建筑物顶端B 的仰角为30°．已知山坡坡度3:4i =，即3tan 4θ=，请你帮助该小组计算建筑物的高度AB ．（结果精确到0.1m 1.732≈）在Rt CDE △中，90E ∠=︒∴222DE CE CD +=∴222(3)(4)20x x +=∴4x =（负值舍去）∴12DE =，16CE =举一反三：【变式1】如图，小文在数学综合实践活动中，利用所学的数学知识测量居民楼的高度AB ，在居民楼前方有一斜坡，坡长15m CD =，斜坡的倾斜角为α，4cos 5α=．小文在C 点处测得楼顶端A 的仰角为60︒，在D 点处测得楼顶端A 的仰角为30°（点A ，B ，C ，D 在同一平面内）．(1)求C ，D 两点的高度差；(2)求居民楼的高度AB ．（结果精确到1m 1.7≈）AFDF 4三角函数的定义是解答本题的关键．【变式2】如图，希望中学的教学楼AB和综合楼CD之间生长着一棵高度为12.88米的白杨树EF，且其底端B，D，F在同一直线上，BF＝FD＝40米．在综合实践活动课上，小明打算借助这棵树的高度测算出综合楼的高度，他在教学楼顶A处测得点C的仰角为9°，点E的俯角为16°．问小明能否运用以上数据，得到综合楼的高度？若能，请求出其高度（结果精确到0.01米）；若不能，说明理由．（解答过程中可直接使用表格中的数据哟！）【答案】能，综合楼的高度约是37.00米．【分析】在Rt△AEG中，利用正切函数求得AG的长，在Rt△ACH中，利用正切函数求得CH的长，据此求解即可得到综合楼的高度．解：小明能运用以上数据，得到综合楼的高度，理由如下：作EG⊥AB，垂足为G，作AH⊥CD，垂足为H，如图：·类型二、解直角三角形的应用——方位角问题2．小明学了《解直角三角形》内容后，对一条东西走向的隧道AB进行实地测量．如图所示，他在地面上点C处测得隧道一端点A在他的北偏东15︒方向上，他沿西北方向前进D，此时测得点A在他的东北方向上，端点B在他的北偏西60︒方向上，（点A、B、C、D在同一平面内）(1)求点D与点A的距离；(2)求隧道AB的长度．（结果保留根号）举一反三：【变式1】如图，我国某海域有A，B，C三个港口，B港口在C港口正西方向33.2nmile （nmile是单位“海里”的符号）处，A港口在B港口北偏西50°方向且距离B港口40nmile 处，在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船，求货船与A港口之间的距离．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19，sin53°≈0.80，cos53°≈0.60，tan53°≈1.33．）由题意得：EF=BC=33.2海里，【变式2】如图，AB 为东西走向的滨海大道，小宇沿滨海大道参加“低碳生活·绿色出行”健步走公益活动．小宇在点A 处时，某艘海上观光船位于小宇北偏东68︒的点C 处，观光船到滨海大道的距离CB 为200米．当小宇沿滨海大道向东步行200米到达点E 时，观光船沿北偏西40︒的方向航行至点D 处，此时，观光船恰好在小宇的正北方向，求观光船从C处航行到D 处的距离．（参考数据：sin 400.64︒≈，cos 400.77︒≈，tan 400.84︒≈，sin 680.93︒≈，cos680.37︒≈，tan 68 2.48︒≈）类型三、解直角三角形的应用——坡度坡比问题来的37°减至30°，已知原电梯坡面AB的长为8米，更换后的电梯坡面为AD，点B延伸至点D，求BD的长．（结果精确到0.1米．参考数据：︒︒︒）≈≈≈≈sin370.60,cos370.80,tan37 1.73【答案】约为1.9米【分析】根据正弦的定义求出AC，根据余弦的定义求出BC，根据正切的定义求出CD，结合图形计算，得到答案．举一反三：【变式1】如图是某水库大坝的横截面，坝高20m CD =，背水坡BC 的坡度为11:1i =．为了对水库大坝进行升级加固，降低背水坡的倾斜程度，设计人员准备把背水坡的坡度改为2i =求背水坡新起点A 与原起点B 之间的距离． 1.41≈ 1.73≈．结果精确到0.1m）【变式2】宜宾东楼始建于唐代，重建于宜宾建城2200周年之际的2018年，新建成的东楼（如图1）成为长江首城会客厅、旅游休闲目的地、文化地标打卡地．某数学小组为测量东楼的高度，在梯步A处（如图2）测得楼顶D的仰角为45°，沿坡比为7：24的斜坡AB前行25米到达平台B处，测得楼顶D的仰角为60°，求东楼的高度DE．（结果精确到1≈）1.7≈ 1.4【点拨】本题考查了解直角三角形的实际应用，掌握三角形中的边角关系是解题的关键．类型四、解直角三角形的应用——其他问题4．2022年6月5日，“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射．如图是处于工作状态的某型号手臂机器人示意图，OA 是垂直于工作台的移动基座，AB 、BC 为机械臂，1OA =m ，5AB =m ，2BC =m ，143ABC ∠=︒．机械臂端点C 到工作台的距离6CD =m ．(1)求A 、C 两点之间的距离；(2)求OD 长．（结果精确到0.1m ，参考数据：sin 370.60︒≈，cos370.80︒≈，tan 370.75︒≈ 2.24≈）【答案】(1)6.7m(2)4.5m【分析】（1）连接AC ，过点A 作AH BC ⊥，交CB 的延长线于H ，根据锐角三角函数定义和勾股定理即可解决问题．（2）过点A 作AG DC ⊥，垂足为G ，根据锐角三角函数定义和勾股定理即可解决问题．．∴==m．OD AG4.5答：OD的长为4.5m．【点拨】求角的三角画数值或者求线段的长时，我们经常通过观察图形将所求的角成者线段转化到直角三角形中（如果没有直角三角形，设法构造直角三角形），再利用锐角三角画数求解【变式1】某型号飞机的机翼形状如图所示，根据图中数据计算AB的长度（结果保留≈）.1.7∠=︒FDB45,∴=，DF FB【变式2】小强在物理课上学过平面镜成像知识后，在老师的带领下到某厂房做验证实验.如图，老师在该厂房顶部安装一平面镜MN ，MN 与墙面AB 所成的角∠MNB =118°，厂房高AB =8m ，房顶AM 与水平地面平行，小强在点M 的正下方C 处从平面镜观察，能看到的水平地面上最远处D 到他的距离CD 是多少?（结果精确到0.1m ，参考数据：sin34°≈0.56，tan34°≈0.68，tan56°≈1.48）【答案】11.8m【分析】过M 点作ME ⊥MN 交CD 于E 点，证明四边形ABCM 为矩形得到CM=AB =8，∠NMC =180°-∠BNM=62°，利用物理学入射光线与反射光线之间的关系得到∠EMD =∠EMC ，且∠CME =90°-∠CMN =28°，进而求出∠CMD =56°，最后在Rt △CMD 中由tan ∠CMD 即可求解．解：过M 点作ME ⊥MN 交CD 于E 点，如下图所示：∵C点在M点正下方，∴CM⊥CD，即∠MCD=90°，∵房顶AM与水平地面平行，∴四边形AMCB为矩形，【点拨】本题借助平面镜入射光线与反射光线相关的物理学知识考查了解直角三角形，解题的关键是读懂题意，利用数形结合的思想解答．。

方位角和俯仰角的取值范围
方位角和俯仰角是空间中位置和方向的两个重要参数。

方位角指
的是某一点相对于某一基准点的方向角度，通常用度数表示，数值范
围为0-360度。

在天文学中，方位角指的是某一恒星相对于地球观测
者的方向角度。

例如，在北半球，北极点的方位角为0度，东方的方
位角为90度，南方的方位角为180度，西方的方位角为270度。

俯仰角是指某一点或某一物体相对于水平面的仰角或俯角。

在天
文学中，俯仰角通常指的是天空中某一恒星或行星相对于地平线的仰
角或俯角。

俯仰角一般用度数表示，其数值范围为-90度到90度。

例如，在北半球观测到的天空中，天顶的俯仰角为90度，地平线的俯仰
角为0度，而南方的天空中某一星座的俯仰角则需要具体情况具体分析。

方位角和俯仰角的测量是天文学研究和定位的重要工具。

通过测
量一个天体的方位角和俯仰角，就可以确定其在天空中的位置。

同时，方位角和俯仰角也被广泛应用于导航、航空、地质、军事等领域。

在
实际使用过程中，为了避免混淆，通常将方位角和俯仰角分别用不同
的符号表示，例如方位角用“Az”表示，俯仰角用“Alt”表示。

这样
就方便人们在探索和研究天文学、地质学、军事等领域时更有效地使
用这些参数。

方位角和俯仰角的取值范围方位角和俯仰角是天文学中常用的两个角度参数，用于描述天体在天空中的位置。

方位角指的是天体相对于北极点的方向角度，俯仰角则是天体相对于地平面的高度角度。

在天文观测中，方位角和俯仰角的取值范围对于观测的准确性和有效性具有重要意义。

方位角的取值范围通常是0°到360°之间，以北极点为基准，顺时针方向为正。

北极点的方位角为0°，东方为90°，南方为180°，西方为270°。

在实际观测中，方位角的取值范围可以根据观测场地的位置和观测目标的运动轨迹进行调整。

例如，在地球表面观测行星运动时，方位角的取值范围会随着行星的位置和运动方向而变化。

俯仰角的取值范围通常是0°到90°之间，以地平面为基准，垂直于地面为正。

观测目标的俯仰角越高，其在天空中的位置就越高。

在实际观测中，俯仰角的取值范围也会随着观测场地的位置和观测目标的高度而变化。

例如，在赤道地区观测天体时，俯仰角的取值范围可以达到90°，而在北极地区观测时则可能只有20°左右。

方位角和俯仰角的取值范围对于天文观测的准确性和有效性具有重要意义。

首先，正确设置方位角和俯仰角的取值范围可以确保观测目标在天空中的位置被准确地确定和记录。

其次，合理地设置方位角和俯仰角的取值范围可以提高观测的效率和准确性，避免观测误差和重复观测的浪费。

最后，方位角和俯仰角的取值范围还可以帮助天文学家更好地理解天体在天空中的运动规律和变化趋势，为天文学研究提供更加准确和全面的数据支持。

综上所述，方位角和俯仰角是天文学中常用的两个角度参数，其取值范围对于天文观测的准确性和有效性具有重要意义。

正确设置方位角和俯仰角的取值范围可以确保观测结果的准确性和完整性，为天文学研究提供重要的数据支持。

方位角和俯仰角的定义
方位角和俯仰角是天文学中常用的两个概念，用来描述天体在观测者视线方向上的位置。

方位角描述了天体与观测者的连线与北方向的夹角，而俯仰角则描述了天体相对于观测者视线的高度角。

方位角通常以度数来表示，从0度开始逆时针旋转，一直到360度。

当方位角为0度时，表示天体位于正北方向；90度表示东方；180度表示正南方；270度表示西方。

方位角的计算可以借助罗盘或者通过天体在天球上的坐标计算得到。

而俯仰角则表示了观测者视线与天体间的垂直夹角。

当俯仰角为0度时，表示天体位于观测者正上方；90度则表示天体在地平线上；当俯仰角超过90度时，表示天体在地平线以下。

掌握方位角和俯仰角的概念对于天文观测是至关重要的。

在进行天体观测时，观测者需要准确地确定天体在视线方向上的位置，才能精确测量其位置和运动。

方位角和俯仰角的测量也是天文仪器设计和编程的基础，帮助观测者确定观测目标的位置和朝向。

在实际观测中，观测者通常会使用专业的天文仪器来测量方位角和俯仰角。

例如，望远镜、天文定位仪等设备可以测量出星体在天球上的坐标，然后根据观测者所处地理位置，计算出相应的方位角和俯仰角。

除了天文观测，方位角和俯仰角的概念也在其他领域有所应用。

例如，无人机、导航系统、航空航天等领域都需要确定目标的方位角和俯仰角，以便准确控制和引导。

总结来说，方位角和俯仰角是天文学中用于描述天体位置的重要概念。

准确测量方位角和俯仰角对于天文观测和其他领域的定位和导航都是至关重要的。

学习和掌握方位角和俯仰角的概念将有助于我们更好地理解天文现象，并在实践中应用这些知识。