当前位置：文档之家 › 浅谈非线性回归模型的线性化

浅谈非线性回归模型的线性化

  • 格式：doc
  • 大小：141.00 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

非线性回归模型的线性化

非线性回归模型的线性化

k 1 beatut yt
k 1 beatut yt
ln
k yt
1
ln b at
ut
令yt
ln
k yt
1
,
b
ln b
yt b at ut
此时可用最小二乘法估计b*和a。
钉螺存活率曲线 （生长曲线模型）
把一批钉螺埋入土中，以后每隔一个月取出部分钉螺，检 测存活个数，计算存活率。数据见表。
FOOD
3000
2000
1000
0 0
4000
8000
12000
INCOME 16000 20000
9.0 LOG(FOOD)
8.5
8.0
7.5
7.0
6.5
6.0 LOG(LOG(INCOME))
5.5 1.80 1.85 1.90 1.95 2.00 2.05 2.10 2.15 2.20 2.25 2.30
以1为例
1
yt xt1
线性模型中的回归系数（边际系数）是对数线性回归模型中弹性
系数的一个分量。
应用柯布-道格拉斯生产函数模型评价台湾省农业生产 效率。利用台湾省1958-1972年农业生产总值yt、劳动力 投入xt1、资本投入xt2的数据估计模型如下：
Yˆt
0.035X
1.5 t1
X
0.49 t2
yt ke be at
yt ke be at
曲线的上限和下限分别为k和0 。
当a 0, Limyt k, 当a 0,b 0 , Limyt 0
t
t
曲线有拐点，坐标为 Lnb , k
a e
, 但曲线不对称于拐点。
一般情形，上限值k可事先估计，有了k值，龚伯斯曲线才 可以用最小二乘法估计参数。

计量经济学非线性回归模型的线性化

计量经济学非线性回归模型的线性化
1. 非标准线性回归模型的线性化方法
变量替换法
Y 0 1 f1 ( X 1 , X 2 ,, X k ) 2 f 2 ( X 1 , X 2 ,, X k ) p f k ( X 1 , X 2 ,, X k ) u
变量替换公式为 Z1 f1 ( X 1 , X 2 ,, X k )
第一节 变量间的非线性关系
第二类：可线性化的非线性回归模型
此类模型可通过适当的变换化为标准的线性回归模型。 如，柯布—道格拉斯（Cobb-Dauglas）生产函数模型，简 称C-D生产函数模型：
Y AK L e

u
其中，Y 表示产出量，K 表示资金投入量，L 表示劳动投入 量，A 为效率系数， 和 非别为K 和 L的产出弹性，A、 和 均为待估未知参数。 取对数后：
第四章 非线性回归模型的线性化
第一节：变量间的非线性关系 第二节：线性化方法 第三节：案例分析
第一节 变量间的非线性关系
1. 线性回归模型与非线性回归模型的形式有何不同？
线性模型
Y 0 1 X 1 2 X 2 k X k u
非线性模型 Y f ( X 1 , X 2 ,, X k ; 0 , 1 ,, p ) u
ln Y ln A
Z f ( X , X ,, X ) 2 2 1 2 k Z k f k ( X 1 , X 2 , , X k )
则
Y 0 1 Z1 p Z p u
第二节 线性化方法
（1）多项式函数模型
Yi 0 1 X i 2 X i k X k ui
就可以得到线性回归模型的一组新的最小二乘估计量。 第三步：将非线性函数 f 在这组新的参数估计值 附近作泰勒级数展开，线性化后得到一个新的标准线性回 归模型。对这个新的标准线性回归模型再应用普通最小二

非线性模型的线性化方法

非线性模型的线性化方法
线性化方法可以将复杂的非线性模型简化为线性模型，使得模型更 容易理解和分析。
提高计算效率
线性模型通常具有更简单的计算形式，可以更快地求解，提高模型 的计算效率。
扩展应用范围
线性模型在许多领域都有广泛的应用，线性化方法可以扩展非线性模 型的应用范围。
缺点
近似误差
线性化方法通常是对非线性模型 的近似，可能引入一定的误差， 特别是在非线性较强的模型中。
考虑模型的物理意义和实际应用背景，选择一个具有代表性的
点作为线性化点。
通过交叉验证和比较不同线性化点的拟合效果，选择最优的线
03
性化点。
对非线性模型进行线性化转换
01
02
03
将非线性模型在所选的 线性化点处进行泰勒级 数展开，得到线性化模
型。
保留级数展开的前几项 ，舍弃高阶项以避免过
拟合。
根据实际需求和数据特 点，选择适合的线性化 方法，如对数转换、幂
非线性模型的特点
复杂性和不确定性
非线性模型通常具有复杂性和不确定性，难以预测和控制。
动态性和时变性
非线性模型中的变量通常具有动态性和时变性，即随着时间的推 移，变量之间的关系可能会发生变化。
相互作用和耦合
非线性模型中的变量之间通常存在相互作用和耦合，即一个变量 的变化可能会对其他变量产生影响。
非线性模型的应用场景
函数转换等。
验证线性化模型的准确性
01
使用独立的数据集对线性化后的模型进行验证，评估其预测 精度和稳定性。
02
比较线性化模型和非线性模型在验证数据集上的表现，以评 估线性化的效果。
03
如果线性化后的模型表现不佳，可能需要重新选择线性化点 或尝试其他线性化方法。

计量经济学第四章非线性回归模型的线性化

计量经济学第四章非线性回归模型的线性化

第四章 非线性回归模型的线性化以上介绍了线性回归模型。

但有时候变量之间的关系是非线性的。

例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述非线性回归模型是无法用最小二乘法估计参数的。

可采用非线性方法进行估计。

估计过程非常复杂和困难，在20世纪40年代之前几乎不可能实现。

计算机的出现大大方便了非线性回归模型的估计。

专用软件使这种计算变得非常容易。

但本章不是介绍这类模型的估计。

另外还有一类非线性回归模型。

其形式是非线性的，但可以通过适当的变换，转化为线性模型，然后利用线性回归模型的估计与检验方法进行处理。

称此类模型为可线性化的非线性模型。

下面介绍几种典型的可以线性化的非线性模型。

4.1 可线性化的模型⑴ 指数函数模型y t = t t ubx ae + (4.1)b >0 和b <0两种情形的图形分别见图4.1和4.2。

显然x t 和y t 的关系是非线性的。

对上式等号两侧同取自然对数，得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。

其中u t 表示随机误差项。

010203040501234XY 1图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =tt u bx ae+, (b < 0)⑵ 对数函数模型y t = a + b Ln x t + u t (4.4)b >0和b <0两种情形的图形分别见图4.3和4.4。

x t 和y t 的关系是非线性的。

令x t * = Lnx t , 则y t = a + b x t * + u t (4.5)变量y t 和x t * 已变换成为线性关系。

图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶ 幂函数模型y t = a x t b t u e (4.6)b 取不同值的图形分别见图4.5和4.6。

04-非线性回归模型的线性化

04-非线性回归模型的线性化
t
i l
2 t
2
2016/3/29
6
4.2、线性化方法
1、 被解释变量与解释变量之间不存在线性关系，与
未知参数之间存在线性关系的模型，其线性化的方法 为：变量替换法；然后利用OLS估计参数。 2、被解释变量与解释变量、未知参数之间不存在线性 关系，但可线性化的模型的线性化方法为：对数法和 变量替换法；然后利用OLS估计参数。 3、真正意义上的非线性模型，需要进行线性化处理。
2016/3/29 5
4.1.3、非线性回归模型的基本假定
1．扰动项零均值： E(u ) 0, t 1, 2,..., n 2．无自相关性： E(u u ) 0; i, l 1, 2,..., n; i l 3．同方差性： E(u ) , t 1, 2,..., n ，其中为有限常 数。 4．解释变量为非随机变量 5．函数性质：一般情况下，假设 f (xt , β)为二阶连 续可微函数。 6．模型参数可识别 7．分布假定：零均值、同方差。在极大似然估 计中，需要对扰动项的分布做出假设，一般假 设其服从正态分布。
ˆ ˆ) log(a 1 ˆ ˆ b
2
ˆ e ) (a
ˆ 1
应当指出，在这种情况下，线性模型估计量
的性质（如 BLUE, 正态性等）只适用于变换后的参 ˆ 和 ˆ ，而不一定适用于原模型参数的估 数估计量 1 2 计量 a ˆ 。 ˆ和 b
2016/3/29 16
CES生产函数模型的线性化回归
最小二乘法
t
ˆ ) min S (β) S (β

min (Yt f (xt , β))2

t
2016/3/29 21
非线性最小二乘法的正规方程组

非线性回归模型的线性化

非线性回归模型的线性化

p f p ( X1, X 2 , , X k ) ＋u
令
Z1 f1(X1, X2, Z2 f2(X1, X2,
, Xk) , Xk)
Zp fp(X1, X2, , Xk )
则可以把原模型转化为一个标准的多元线性回归模型
Y 0 1Z1 2Z2 pZ p u
6
下面介绍在经济问题时经常遇到的几种非标准线性 回归模型
p fp(X1, X2, , Xk )
2024/10/17
5
4.2线性化方法
1、非标准线性回归模型的线性化方法 非标准线性回归模型的线性化方法是变量替换法。
非标准线性回归模型的一般形式为：
Y 0 1 f1( X1, X 2 , , X k ) 2 f2 ( X1, X 2 , , X k )
Yi* bX i ui
2024/10/17
16
（2）幂函数模型（全对数模型）
幂函数模型的一般形式为：
Yi
AX
1 1i
X
2 2i
X e k ui ki
对上式两边取对数得到：
ln Yi ln A 1 ln X1i 2 ln X 2i k ln X ki ui
令
Yi*
ln Y , 0
在这样一些非线性关系中，有些可以通过代数 变换变为线性关系处理，另一些则不能。下面我们 通过一些例子来讨论这个问题。
2024/10/17
1
线性模型的含义
线性模型的基本形式是:
Y 0 1X1 2 X 2 ...... k X k u
线性模型的线性包含两重含义：
（1）变量的线性
变量以其原型出现在模型之中，而不是以 X 2 或
（1）多项式函数模型 多项式函数模型的一般形式为：

非线性回归模型的线性化

非线性回归模型的线性化以上介绍了线性回归模型。

但有时候变量之间的关系是非线性的。

例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述非线性回归模型是无法用最小二乘法估计参数的。

可采用非线性方法进行估计。

估计过程非常复杂和困难，在20世纪40年代之前几乎不可能实现。

计算机的出现大大方便了非线性回归模型的估计。

专用软件使这种计算变得非常容易。

但本章不是介绍这类模型的估计。

另外还有一类非线性回归模型。

其形式是非线性的，但可以通过适当的变换，转化为线性模型，然后利用线性回归模型的估计与检验方法进行处理。

称此类模型为可线性化的非线性模型。

下面介绍几种典型的可以做线性化处理的非线性模型。

⑴ 指数函数模型y t = t t u bx ae + (4.1) b >0 和b <0两种情形的图形分别见图4.1和4.2。

显然x t 和y t 的关系是非线性的。

对上式等号两侧同取自然对数，得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。

其中u t 表示随机误差项。

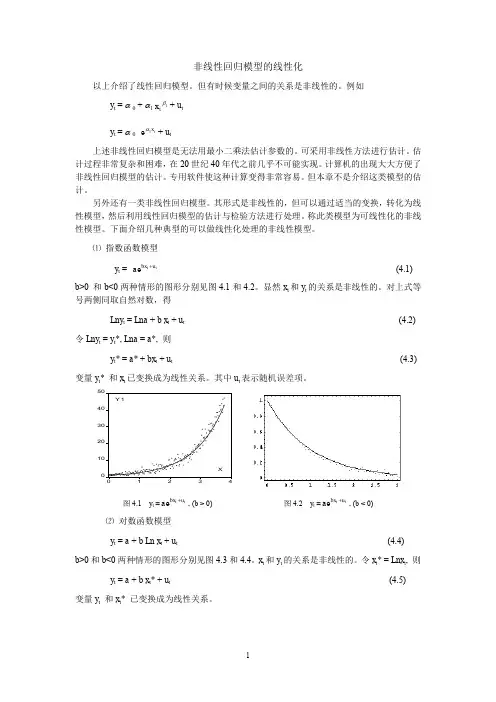
010203040501234XY 1图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =tt u bx ae+, (b < 0)⑵ 对数函数模型y t = a + b Ln x t + u t (4.4)b >0和b <0两种情形的图形分别见图4.3和4.4。

x t 和y t 的关系是非线性的。

令x t * = Lnx t , 则y t = a + b x t * + u t (4.5)变量y t 和x t * 已变换成为线性关系。

图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶幂函数模型y t= a x t b t u e(4.6)b取不同值的图形分别见图4.5和4.6。

非线性回归模型的线性化讲解


( b1>0, b2>0)
(b1<0, b2 <0
（2） 双曲函数模型
1 1 ui 双曲函数模型的一般形式为： Yi Xi 1 1 令 * * Yi , Xi Yi Xi
则可将原模型化为标准的线性回归模型
Yi X ui
* * i
双曲线函数还有另一种表达方式，
ln GDP i ln A ln Ki ln Li ui
Yi ln GDP i , X 1i ln Ki , X 2i ln Li
0 ln A, 1 , 2 则可将C-D生产函数模型转换成标准的二元线性回归模型
Yi 0 1 X1i 2 X 2i ui

Z p f p ( X1, X 2 ,, X k )
Y 0 1Z1 2 Z2 p Z p u
7
下面介绍在经济问题时经常遇到的几种非标准线性 回归模型 （1）多项式函数模型
多项式函数模型的一般形式为：
Yi 0 1 X i 2 X i2 k X ik ui
首先对上式做倒数变换得：
1 e X i ui Yi
令
1 Yi , X i* e X i Yi
*
则可将原模型化为标准的线性回归模型
Yi* X i* ui
15
2 可线性化的非线性回归模型的线性化方法
下面几种在研究经济问题时经常遇到的可线性化的非线性 回归模型 （1）指数函数模型
yt = b0 +b1 x 1t + b2 x 2t + b3 x 3t + ut 这是一个三元线性回归模型。如经济学中的总成本与产 品产量曲线与左图相似。

非线性回归的线性化处理


例10.7 某钢厂出钢时所用的盛钢水的钢包，由于钢水对耐火材 料的侵蚀，容积不断扩大. 通过试验，得到了使用次数x 和钢包增 大的容积y 之间的17组数据，如表10-6 . 求使用次数x 与增大容积y 的回归方程.
解 散点图如图10 - 8.
看起来y 与x 呈倒指数关系
ln y a b 1
其中a ， b ， σ2 为与t无关的未知参数，只要令x=sint ， 即可将 (10.29)化为(10.1).
y a bt ct2 , N (0 , 2 )
（10.30）
其中a ， b ， c ， σ2 为与t无关的未知参数，只要令x1=t ， x2=t2得
y a bx1 cx2 , N (0 , 2 )
概率学与数理统计
非线性回归的线性化处理
前面讨论了线性回归问题，对线性情形我们有了一整套 的理论与方法. 在实际中常会遇见更为复杂的非线性回归问 题，此时一般是采用变量代换法将非线性模型线性化，再 按照线性回归方法进行处理. 举例如下:
y a bsin t , N (0 , 2 )
（10.29）
x
记
y ' ln y , x ' 1
x
求出x ′ y′的值，表10-7所示.
作（x ′ , y′)的散点图，如图10-9所示.
可见各点基本上在一直线上,故可设
y ' a bx ' , (0 , 2 )
经计算，得
x ' 0.1464 , y ' 2.2963
n
(x 'i )2 0.5902 ,
i 1
n
( y 'i )2 89.93;i y 'i 5.4627 ,

计量经济学-第四章-非线性回归模型的线性化25页


（1）指数函数模型
Yi AebXiui 取对数 ln Y i ln AbiX ui
令
Y* i
lnYi,alnA则
Yi*abX i ui

（2）幂函数模型
Y i A1 i1 X X 2 2 i1 X k kieui
lY i n lA n 1 lX n 1 i 2 lX n 2 i k lX n k i u i
2. 非线性回归模型可分为几类？
第一类：非标准的线性回归模型； 第二类：可线性化的非线性回归模型； 第三类：不可线性化的非线性回归模型。
第一节 变量间的非线性关系
第一类：非标准的线性化模型 Y与解释变量 X1,X2,,Xk 之间不存在线性关系，
但与未知参数 0,1,2,之,间p 存在线性关系。
Y 01f1 (X 1 ,X 2 , ,X k)2f2 (X 1 ,X 2 , ,X k) 举例：总成 本 函数pf模k(X 型1 ,X 2 , ,X k) u
C 01 X 2 X 23 X 3 u
第一节 变量间的非线性关系
第二类：可线性化的非线性回归模型
此类模型可通过适当的变换化为标准的线性回归模型。 如，柯布—道格拉斯（Cobb-Dauglas）生产函数模型，简 称C-D生产函数模型：
YA K Leu
其中，Y 表示产出量，K 表示资金投入量，L 表示劳动投入
Y i AiK L ieui,i1 ,2 , ,n
其中，Y 表示产出量，K 表示资金投入量，L表示劳
动投入量，u 表示随机误差项，A、、为未知参
数。试利用天津市1980年~2019年间的有关统计资 料，估计天津市全社会的C-D生产函数模型。 解：详见教材。
第二节 线性化方法
3. 不可线性化的非线性回归模型的线性化估计方法
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

浅谈非线性回归模型的线性化
广东省惠州市惠阳区崇雅中学高中部 卢瑞勤(516213)
回归分析在各个领域中都有十分重要的作用，比如：在财务中可以用回归分析进行财务预测；在医疗检验中可以用回归分析进行病理预报等等。

高中新课标教材就在《必修3》和《选修2-3》中分别增加了《线性回归》和《回归分析》的内容，介绍了求线性回归方程的方法。

但在实际问题中，变量间的关系并非总是线性关系，本文结合本人的教学实践，对教材中的这两部分内容进行适当延伸，谈谈对一些可线性化的非线性回归模型的线性化问题，供各位同行在教学时参考。

一、什么是可线性化的非线性回归模型
线性回归模型的基本特征是预报变量可以表示成解释变量和一个系数相乘的和，即预报变量y 可以表示成解释变量i x (i =1，2，3，……)的如下形式：0112233y a a x a x a x =++++
，其中变量i
x 是以其原型(而不是以n
i x 或其它)的形式出现，变量y 是各变量i x 的线性函数。

而有些回归模型不具备这个特点，但是可以通过适当的代数变换转化成这种形式，我们称这类回归模型为可线性化的回归模型。

在本文中，我们只讨论只有一个解释变量可线性化的非线性回归模型的线性化。

二、非线性回归模型的线性化的基本思路
非线性回归模线性化的基本思路是：由已知数据，确定解释变量和预报变量，作出散点图，根据经验，确定回归曲线的类型，然后作适当的代数变换，若变换后散点图体现较好的线性关系，即可将其化成线性形式求解，最后还原到原来的回归曲线。

如果回归曲线可用多种形式表示，可以各自将其线性化后求解，再用相关系数2
R 进行拟合效果分析，2
R 越大，拟合效果越好，所求的回归方程也就越精确。

三、非线性回归模型的线性化的常用方法
可线性化的非线性回归模型有以下几种常见类型：
(1)双曲线型，其形式为
1a b y x =+，其变换为1y y '=， 1
x x
'=，变换后的形式为y b ax ''=+ (2)幂函数型，其形式为b
y ax = ，可以变形为ln ln ln y a b x =+，作变换ln y y '= ，ln x x '= ，变换后的形式为y a bx ''=+
(3)指数函数型，其形式为bx
y ae = ，以变形为ln ln y a bx =+，作变换ln y y '=，ln a a '= ，变换后的形式为y a bx ''=+
(4)对数函数型，其形式为ln y a b x =+，作变换ln x x '=，变换后的形式为y a bx '=+ 下面以高中新课标数学教材《选修2-3》一道习题为例加以说明
【例】在某地区的一段时间内观察到的不小于某震级x 的地震个数y 数据如下表，试建立回归方程表述二者之间的关系。

解：作出散点图，如图1，可以看出回归类型是指数型或对数型。

若采用指数型回归曲线，可设回归曲线为bx
y ae =，变形为ln ln y a bx =+，作变换ln y y '=，
此时，以(x ，ln
y )为点作散点图，如图2，可以看出x 和ln y (即y ')有较强的线性关系。

(图1) (图2) (图3)
以x 为解释变量，以ln y 为预报变量，用最小二乘法求得回归直线方程为10.65630.341y x =-，
10.6563a '=，从而10.656342459.2a e ==
此时所求的归回曲线方程为：(1)
0.341ˆ42459.2x y
e -=，其相关系数21R =0.9973
若采用幂函数型回归曲线，则可设回归曲线方程为b
y ax =，即ln ln ln y a b x =+，令ln y y '=，
以(ln x ，ln y )为点作散点图，如图3所示。

再以ln x 为解析变量，以ln y 为预报变量用最小二乘法求得回归直线方程为8.082819.663y x =-+，因为ln 19.663a a '==，所以8
3.463610a =⨯
此时所求的回归曲线方程为：(2)
88.0828ˆ 3.463610y
x -=⨯，其相关系数2
2
0.9785R = 因为22
12R R >，所以采用指数型回归类型曲线的拟合效果较好，其回归曲线方程为
0.341
ˆ42459.2x
=
y e-
以上只是对几种非线性回归模型的线性化方法初探，应该说明的是，并不是所有的非线性回归模型都可以线性化，即使是可线性化，也不限以上几种方法；同时在教学中，如果条件允许，可以用Excel结合实例对照讲解，帮助学生选择适当的回归曲线类型，加深对非线性回归模型线性化的认识，收到举一反三的效果。