当前位置：文档之家 › 优选哈工大信号检测与处理确知和随机参量信号检测

优选哈工大信号检测与处理确知和随机参量信号检测

  • 格式：ppt
  • 大小：1.95 MB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

哈工大随机信号实验报告

哈工大随机信号实验报告

H a r b i n I n s t i t u t e o f T e c h n o l o g y实验报告课程名称：随机信号分析院系：电信学院班级： 1205201 姓名：学号：指导教师：郑薇实验时间： 2014年 11月哈尔滨工业大学实验一 各种分布随机数的产生一、 实验目的在很多系统仿真的过程中，需要产生不同分布的随机变量。

利用计算机可以很方便地产生不同分布的随机变量，各种分布的随机变量的基础是均匀分布的随机变量。

有了均匀分布的随机变量，就可以用函数变换等方法得到其他分布的随机变量。

二、 实验内容产生均匀分布的随机数、高斯分布的随机数和其它分布的随机数。

三、 实验原理1. 均匀分布随机数的产生原理产生伪随机数的一种实用方法是同余法，它利用同余运算递推产生伪随机数序列。

最简单的方法是加同余法)(m od 1M c y y n n +=+My x n n 11++=为了保证产生的伪随机数能在[0,1]内均匀分布，需要M 为正整数，此外常数c 和初值y0亦为正整数。

加同余法虽然简单，但产生的伪随机数效果不好。

另一种同余法为乘同余法，它需要两次乘法才能产生一个[0,1]上均匀分布的随机数)(m od 1M ay y nn =+M y x n n 11++=式中，a 为正整数。

用加法和乘法完成递推运算的称为混合同余法，即)(m od 1M c ay y n n +=+My x n n 11++=用混合同余法产生的伪随机数具有较好的特性，一些程序库中都有成熟的程序供选择。

常用的计算语言如Basic 、C 和Matlab 都有产生均匀分布随机数的函数可以调用，只是用各种编程语言对应的函数产生的均匀分布随机数的范围不同，有的函数可能还需要提供种子或初始化。

Matlab 提供的函数rand()可以产生一个在[0,1]区间分布的随机数，rand(2,4)则可以产生一个在[0,1]区间分布的随机数矩阵，矩阵为2行4列。

哈尔滨工程大学 随机信号分析02-04

哈尔滨工程大学 随机信号分析02-04

随机信号分析第二章（4）哈尔滨工程大学信息与通信工程学院t0tt0()X t ()X t ()X t ()X ttt()X t (X t一、遍历性过程的定义如果一个随机过程X (t ),它的各种时间平均 （时间足够长）依概率1 收敛于相应的集 合平均,则称X (t )具有严格遍历性,并称该过程为严格遍历性过程，简称严遍历过程。

1.严遍历性的定义1()()lim()d 2T TT A X t X t X t tT−→∞<>==∫1(,)()()lim()()d 2T X TT t t X t X t X t X t tTτττ−→∞ℜ+=+=+∫2. 随机过程的时间平均1）X (t ) 的时间均值2）X (t ) 的时间自相关函数A <⋅>()⋅符号依概率1成立则称过程X (t )的均值具有遍历性。

()()[()]XA X t X t E X t m <>===3. 平稳过程X (t ) 的均值和自相关函数具有遍历性(1) 均值具有遍历性如果即，时间均值依概率1收敛于集合均值。

依概率1成立，则称X (t )的自相关函数具有遍历性。

(2) 自相关函数具有遍历性如果即，时间自相关函数依概率1收敛于集合自相关函数。

(,)()()[()()]()X X t t X t X t E X t X t R ττττℜ+=+=+=依概率1成立，则称X (t )的均方值具有遍历性。

均方值具有遍历性如果(,)()()[()()](0)X X t t X t X t E X t X t R ℜ===4. 宽遍历性的定义设X (t) 是一个平稳随机过程, 如果其均值和自相关函数都具有遍历性, 则称X (t) 为宽遍历性过程( 或广义遍历性过程), 简称遍历过程。

二、遍历性的实际应用一般随机过程的时间平均是随机变量，但遍历过程的时间平均为确定量，因此可用任一样本函数的时间平均代替整个过程的统计平均，在实际工作中，时间T 不可能无限长，只要足够长即可。

哈工大信号检测与处理第1章随机过程15-1

哈工大信号检测与处理第1章随机过程15-1

1.2 高斯分布与高斯噪声
2 x ( t ) 式中， a 为噪声 的均值； 为噪声 x ( t ) 的方差。称 x ( t ) 是服从均值为 a ， 2 2 x ( t ) ~ N ( a , ) 。 为标准差。特别当 方差为 的高斯分布或正态分布，记作 2 a 0 ， 1 时， x ( t ) 的分布称为标准正态分布。
1
1.2.3 高斯分布特性的应用
高斯分布最直观的应用是考虑其对数据处理影响程度的分析，如 3 法则。 ： 3 法则（标准） 该法则的意义是当噪声服从高斯分布时，噪声的影响主要集中在正负3 倍的标准差之内，即1σ 只考虑了68%的噪声影响，而3σ 几乎考虑了其全部 影响。 大多数噪声（随机过程）瞬时幅度的概率分布是正态的即
F ( x) 1 2
xa xa
用误差函数表示 F(x)的好处是，借助于一般数学手册所提供的误差函数表，可方 便查出不同 x 值时误差函数的近似值，还可以在 Matlab 程序中直接调用 erf(x) 或 erfc(x)计算，避免了复杂积分运算。
误差函数和余补误差函数的主要性质： （1）误差函数是递增函数，它具有如下性质 1） erf ( x) erf ( x) ； 2） erf () 1 。 （2）余补误差函数是递减函数，它具有如下性质 1） erfc() 0 ； 2） erfc( x) 1 exp(x2 ), x x
1 Pn Pn ( )d R(0) 2 2
2）高斯噪声的一维概率密度函数具有如下特性： （1） p( x ) 对称于 x a 直线，即有
p(a x ) p( a x )
（2） p( x ) 在 ( , a ) 内单调上升，在 ( a , ) 内单调下降， 且在点 a 处达到极大值

哈尔滨工程大学数组信号处理实验三

哈尔滨工程大学数组信号处理实验三

1020304050607080一、实验原理时域抽样定理给出了连续信号抽样过程中信号不失真的约束条件：对于基带信号，信号抽样频率fsam 大于等于2倍的信号最高频率m ，即fsam>=2fm 。

时域抽样是把连续信号x(t)变成适于数字系统处理的离散信号x[k] ；信号重建是将离散信号x[k]转换为连续时间信号x(t)。

1. 信号的时域抽样若x[k]=x(kT)|t=kT ，则信号x(t)与x[k]的频谱之间存在：其中：x(t)的频谱为X(jw)，x[k]的频谱为X(ejW) 可见，信号时域抽样导致信号频谱的周期化。

2. 信号的频域抽样非周期离散序列x[k]的频谱X(ejW)是以2p 为周期的连续函数。

频域抽样是将X(ejW)离散化以便于数值计算。

频域抽样与时域抽样形成对偶关系。

在[0,2p]内对X(ejW) 进行N 点均匀抽样，引起时域序列x[k]以N 点为周期进行周期延拓。

频域抽样定理给出了频域抽样过程中时域不发生混叠的约束条件：若序列x[k]的长度L ，则应有NL 。

二、实验内容（一）抽样引起的混叠正弦信号混叠：可以按抽样频率fs=1/Ts 对x(t)抽样来获得离散时间信号。

a.抽样频率fs=8kHz ，令正弦波频率为300Hz ，然后在10ms 长间隔上抽样，相位任意指定。

使用stem 绘出产生的离散时间信号。

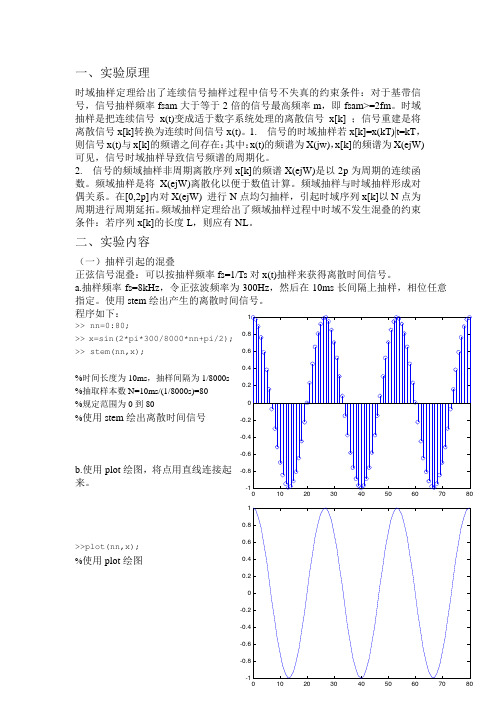
程序如下： >> nn=0:80;>> x=sin(2*pi*300/8000*nn+pi/2);>> stem(nn,x);%时间长度为10ms ，抽样间隔为1/8000s %抽取样本数N=10ms/(1/8000s)=80 %规定范围为0到80%使用stem 绘出离散时间信号b.使用plot 绘图，将点用直线连接起来。

>>plot(nn,x);%使用plot 绘图10203040506070801020304050607080102030405060708010203040506070801020304050607080102030405060708010203040506070801020304050607080c.把正弦的频率从100Hz 变至475Hz ，每次增加125Hz ，绘出一系列相应的图，并用subplot 指令把四个图放在同一张图上。

17哈工大信号检测与估计

17哈工大信号检测与估计
2, H ) ˆ, σ p (x ; A ˆ1 1 >γ 2 p (x ; σ ˆ 0 , H0 )
Li, Wei
Decision Theory
Decision Theory Detection Theory II Generalized Likelihood Ratio Test (GLRT)
2 σ ˆ0 2 ˆ, σ A ˆ1 2 =σ 2. σ ˆ0 ˆ1
2 = Pr {X1 > γ ; H0 }
Example DC level in WGN A unknown, σ 2 unknown. H0 : A = 0, σ 2 > 0 H1 : A = 0, σ 2 > 0 θr = A, θs = σ 2 , r = 1, s = 1 a 2 ⇒ 2 ln LG (x ) ∼ X1 Same as when σ 2 is known-nuisance parameters do not affect threshold but do decrease λ and hence PD . From previous work 2 ln LG (x ) = N ln 1 1−
Unknown
>0
θ=
A σ2
⇒
θr = A θs = σ2
r =1 s=1
Li, Wei
Decision Theory
Decision Theory Detection Theory II Generalized Likelihood Ratio Test (GLRT)
In general we test H0 : θ r H1 : θ r (θr 0 = 0 in example) GLRT is to deci 1 , ˆ θ s 1 , H1 ) >γ p (x ; θ r 0 , ˆ θ s 0 , H0 ) = θr 0 , θs = θr 0 , θs

哈工大信号检测与处理第5章课程5-2新

哈工大信号检测与处理第5章课程5-2新

j '
d
连续小波变换
def 1 CWTx , a, a t x t a
*
dt
二进小波：
1 t 1 t ( ) ( j ) 2 j /2 (2 j t 2 j ) a 2 a 2j
k
(1)

k 1
h
0, 1 k
1,k (t ) 2 (1) k 1 h0, 1 k (2t k ) 。 k

1/ 2, h0,1 1/ 2 ，即 (t ) (2t ) (2t 1)
(1)2 h0,0 1/ 2, d0,2 (1)3 h0,1 1/ 2 ，即

的标准正交基。
5.3 多分辨率分析
例 1：双尺度方程
(t )
k
h

0, k
1,k (t ) 2 h0,k (2t k ) ， h0,k (t ),1,k (t ) 。
k

构造方程： (t ) （1） h0,0
(t ) (2t ) (2t 1)
构造方程（正交小波） ：
1 t [0,0.5) (t ) (2t ) (2t 1) 1 t [0.5,1) 0 other
1
0.7 0.6
构造方程（正交小波） ：
离散小波：
j ,k (t ) 2
j/2
(2 t k 0 )
j
0 1
j ,k (t ) 2 j /2 (2 j t k )
j /2 j j ,k (t ) a0 (a0 t kb0 ) a0 1, b0 0

信号检测与估计

UESTC 何子述
T
12
例 ：雷达目标探测中，
s(t ) = A(t − τ ) cos [ 2π (f 0 +f d )(t − τ ) + φ ]
τ :目标距离
f d:多普勒频率（目标径向速度） 电子侦察中：信号源的方向、信号频率
对参数进行连续的估计，称为跟踪（tracking）
UESTC 何子述
so (t ) = s1 (t ) ∗ β (t )
（如多径效应）
冲激响应 β (t )是随机过程
UESTC 何子述
3
• 本课程仅研究加性噪声中的检测与估计。 • 对乘性噪声的研究采取取对数的方法； • 对卷积噪声取付氏变换再取对数。 即都可以转换为对加性噪声的研究
UESTC 何子述
4
2、加性噪声中的信号类别
UESTC 何子述
异步数字通信中常遇到！
6
雷达回波信号
s (t ) = A(t ) cos[ωo (t − τ ) + φ )]
A(t), τ , φ （3）噪声中的随机信号 ：随机参数
x(t ) = s (t ) + v(t )
随机信号（随机过程） 电子侦察中侦收的信号、地震信号监测、天文观 测信号、被动雷达信号、声纳信号等等！
信号检测与估计 Signal Detection and Estimation
何子述，孔令讲
UESTC 何子述
1
1、信号传输的基本结构
I (t ) 或s1 (t)
接收信号：x(t ) = s (t ) + v(t )
加性噪声
UESTC 何子述 2
乘性噪声：信号在传输过程中幅度发生了变化。 so (t ) = α (t ) s1 (t ) α (t )是随机变化的（如移动通信中的衰落信道）； 卷积噪声：

信号检测与估计研究

信号检测与估计研究信号检测与估计是一门研究如何在噪声和不确定性的环境中准确检测和估计信号参数的学科。

这门学科涉及到很多方面的知识，包括数学、统计学和工程学等。

在现代通信系统、雷达系统、生物医学领域以及金融分析等领域，信号检测与估计起着至关重要的作用。

信号检测与估计的目标是在观测到的数据中检测出存在的信号，并估计信号的参数。

在噪声和不确定性的环境中，这个过程是十分复杂的，需要采用合适的数学模型和算法来解决。

信号检测与估计的核心问题包括信号的检测、参数的估计和最优检测等。

信号检测是指在接收到的信号中判断是否存在感兴趣的信号成分。

在通信系统中，我们常常需要从接收到的信号中判断是否存在发送的信号。

在雷达系统中，我们需要从接收到的回波信号中判断是否存在目标。

而在生物医学领域中，我们常常需要从生理信号中判断是否存在特定的疾病现象。

信号检测的核心问题是如何准确地判断是否存在信号，并且如何在存在信号的情况下有效地提取出信号。

参数估计是指在已知信号存在的情况下，估计出信号的参数。

在通信系统中，我们常常需要估计出发送信号的幅度、相位和频率等参数。

在雷达系统中，我们需要估计出目标的距离、方位和速度等参数。

而在生物医学领域中，我们常常需要估计出生理信号的频率、振幅和相位等参数。

参数估计的核心问题是如何在噪声和不确定性的环境中准确地估计出信号的参数。

最优检测是指在信号检测问题中，如何设计最优的检测算法以达到最佳的检测性能。

最优检测的目标是使得检测器的错误概率最小。

最优检测的核心问题是如何在噪声和不确定性的环境中设计出最佳的检测规则，以使得检测器的错误概率最小。

信号检测与估计的研究涉及到了很多数学、统计学和工程学的知识。

在数学方面，我们需要掌握概率论、统计学、随机过程等知识，以建立信号的数学模型。

在统计学方面，我们需要研究估计方法，以估计出信号的参数。

在工程学方面，我们需要研究信号处理和检测算法，以实现信号的检测与估计。

总结起来，信号检测与估计是一门涉及到数学、统计学和工程学的学科，它在现代通信系统、雷达系统、生物医学领域以及金融分析等领域中起着至关重要的作用。

哈尔滨工业大学科技成果——高精度质量质心测量系统

哈尔滨工业大学科技成果——高精度质量质心测量系统
主要研究内容
哈尔滨工业大学光电信息与检测技术研究所多年来一直从事几何量和质量测量方面的研究工作，曾承担和完成了多项国家和省部级科研课题。

近期研制的质量质心测量系统是一种高精度智能测试仪器，通过称重仪及控制卡一体化设计进行传感器信号的自动切换及采集，实现了质量质心测量过程的自动化和集成化，从而实现了高精度测量。

该测量系统具有广泛的应用领域。

控制电箱软件界面
主要技术指标
测量范围：600-900kg
质量测量准确度：优于0.1%
质心测量不确定度：1.5mm
技术特点及优势
1、控制系统采用称重仪与控制卡一体化设计，减少外界干扰，测量精度高；
2、测量系统安全、稳定、可靠；
3、测量过程全程自动控制，可实现传感器信号的自动切换与采
集，操作简单快捷；
4、测量软件具有友好的人机交互界面，具有数据采集及处理、传感器斜率标定、系统精度检验、测量报告打印等功能。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
哈工大信号检测与处理确知和 随机参量信号检测
因为要在 M 个确知信号中做出选择，故需要 M 个假设。即
H1 : x(t) s1(t) n(t), 0 t T
H
2
:
x(t
)
s2
(t
)
n(t
),
0
t
T
HM : x(t) sM (t) n(t), 0 t T
由于假定各类假设的先验概率相等，且各种错误判决的代价相等，贝叶斯准
2.5.1 复合假设检验—解决依赖于一组参数的信号的存在问题 这里仅讨论两个假设情况，但所用方法可推广到多个假设的情况。 令 (1,2,...n ) 表示与假设 H0 有关的随机参量矢量，这里可令 1 －相
位， 2 －幅度， 3 －频率，……….。
令 (1,2,...n ) 表示与假设 H1 有关的随机参量矢量，这里可令1,2,3... 表 示信号的初相角，幅度，频率，….
因为信号参量的不确定性，观测值 y 的概率不仅与假设有关，而且还依赖于 未知参量的取值，因此，这些条件概率表示为：
p1( y | ) 和 p0( y | ) 。
把表示观测信号的多维空间划分为 R0 ， R1 两部分。
与简单假设时一样，观测信号落在区域 R0 ，就选择假设 H0 ，记作 D0 ；观测
则转化为最大似然准则。即若 P(X Hi ) 最大，则判定 Hi 假设为真。
推广到 M 元的情况，显然有：
P( X
Hi
)
F
exp[
1 N0
T 0
[
x(t
)
si
(t
)]2
dt
]
其中 F 为常数。 显然似然函数随着指数中积分项的减小而增大。因此等效的判决规则为若
T 0
[ x(t )
si
(t)]2
dt
S1(t)
X(t)
积分
S2(t)
选 择 判决 最 大 值
ห้องสมุดไป่ตู้积分
SM(t)
M 元信号的相关接收机
总之，与二元检测问题类似总可以把似然比计算转化为相关接收机的结构形 式
2.5 随机参量信号的检测
必要性：上节假定信号在接收机处是已知的。但实际上，除了噪声干扰引起 观测信号的不确定性外，还有由于信号参量的随机性所引起的附加不确定性。 所以即使能够滤掉相加性噪声，信号参量的随机性引起的不确定性也是依然存在。 因此在多数情况下信号在接收端，其参量发生变化，把含有随机或未知参量的信 号称为随机参量信号。
在此之前考虑的假设是简单假设，即认为信号是确知的，或是存在，或是不 存在。若信号存在，则信号的有关参量如初相角，幅度，频率等都是已知的确定 值。观测信号的随机性只是由于干扰的随机性引起的。 然而，在许多情况下信号并不确知，初相角，幅度，频率等参量一般来说也都是 不确定的即具有随机参量。这样混合信号的概率密度函数中含有未知参量。这种 在概率密度函数中含有未知参量的假设称为复合假设
最小的 R0 的范围。
假定：
c10( ) c00( ) 0
c01( ) c11( ) 0
（2－76）
则由于前两项与 R0 无关，因此当 R0 选成使式（2－75）对 y 的积分项的被积函数 为负值的区域时， c 即为最小值。这样 H0 成立。
判决域 R0 可这样来确定，所有满足
p(H1) p1( y | )p1( )[c01( ) c11()]d p(H0) p0( y |) p0()[c10() c00()]d 0
信号落在区域 R1 ，就选择假设 H1 ，记作 D1 。考虑到信号参量是随机的，每个随
机参量都有自己的概率分布密度，于是平均代价（平均风险）可写为：
c c00(i )p(D0, H0,i ) c10(i )p(D1, H0,i )
i( )
i( )
c01(i )p(D0, H1,i ) c11(i )p(D1, H1,i )
l (y)
p1( y | ) p1( )d
p0( y |) p0()d
H1 H0
p(H0)(c10 c00) p(H1)(c01 c11)
（2－78） （2－79）
注意到
p1(y |)p1() p1(y,), p1(y,)d p1(y)
类似的情况也适用于 H0 假设
（2－80）
p1(y |)p1()d
l (y)
H1
p1(y)
p(H0)(c10 c00)
p0(y |)p0()d
p0
(
y
)
H0
p(H1)(c01 c11)
（2－81）
复合假设检验在形式上就变为简单假设检验，但需要说明，所谓变为简单假
设检验，只是门限的计算与简单假设检验相同，而似然函数的计算多了一次积分，
变为平均似然比，这正是因为随机参量的随机性需要统计平均来表征。
（2－77）
的 y 值划分给 R0 ，判决 H0 成立。把不满足的 y 值划归 R1 域，判决 H1 成立。
于是上式可改写为：
l (y)
p1( y | ) p1( )[c01( ) c11( )]d
p0( y |) p0()[c10() c00()]d
H1 H0
p(H0) p(H1)
若代价函数 cij 与变量 ， 无关，则
令 p0(), p1( ) 分别表示与 ， 有关的联合先验概率。
当应用贝叶斯准则进行判决时，代价函数也可以是 ， 的函数。 但 c00,c10 （与 H0 相关的）可以只是 的函数而与 （信号的参量）无关，
c00(i ),c10(i ) 。
c10,c11 （与 H1相关的）可以只是 的函数而与 无关。c10(i ),c11(i )
最小，则选择相应的
Hi
假设为真。即
T 0
[
x(t)
si
(t)]2
dt
T x(t)2 dt
0
T 0
si (t)2dt
2
T 0
x(t)si (t)dt
由于上式中第一项和第二项的积分同选择哪个假设为真无关，所以判决规则为：
T
Gi 0 x(t)si (t)dt
若 Gi 为最大，则选择相应的 Hi 假设为真。对应的接收机如图所示 积分
i( )
i( )
c p(H0 ) p0( )c10( )d p(H1) p1( )c01( )d
{p(H1) p1( y | ) p1( )[c01( ) c11( )]d
R0
p(H0 ) p0( y | ) p0( )[c10( ) c00( )]d}dy
（2－75）
式中，影响 c 大小的是区间 R0 的选定，应用贝叶斯准则就是要定出使平均代价