ppt直线一级倒立摆

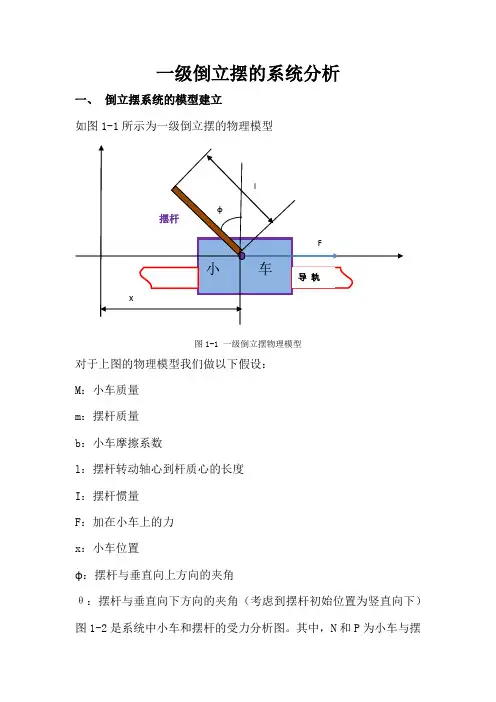
一级倒立摆的系统分析一、倒立摆系统的模型建立如图1-1所示为一级倒立摆的物理模型图1-1 一级倒立摆物理模型对于上图的物理模型我们做以下假设：M：小车质量m：摆杆质量b：小车摩擦系数l：摆杆转动轴心到杆质心的长度I：摆杆惯量F：加在小车上的力x：小车位置ɸ：摆杆与垂直向上方向的夹角θ：摆杆与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下）图1-2是系统中小车和摆杆的受力分析图。

其中，N和P为小车与摆杆相互作用力的水平和垂直方向的分量。

注意：实际倒立摆系统中的检测和执行装置的正负方向已经完全确定，因而矢量方向定义如图所示，图示方向为矢量正方向。

图1-2 小车及摆杆受力分析分析小车水平方向受力，可以得到以下方程：M ẍ＝Ｆ-ｂẋ-Ｎ (1-1)由摆杆水平方向的受力进行分析可以得到以下方程：N =md 2dt 2(x +l sin θ) (1-2)即： N =mẍ+mlθcos θ−mlθ2sin θ (1-3)将这个等式代入式（1-1）中，可以得到系统的第一个运动方程： (M +m )ẍ+bẋ+mlθcos θ−mlθ2sin θ=F (1-4)为推出系统的第二个运动方程，我们对摆杆垂直方向上的合力进行分析，可以得出以下方程： P −mg =md 2dt 2(l cos θ) (1-5)P −mg =− mlθsin θ−mlθ2cos θ (1-6) 利用力矩平衡方程可以有：−Pl sinθ−Nl cosθ=Iθ (1-7)注意：此方程中的力矩方向，由于θ=π+ɸ，cosɸ=−cosθ，sinɸ=−sinθ，所以等式前面含有负号。

合并两个方程，约去P和N可以得到第二个运动方程：(I+ml2)θ+mgl sinθ=−mlẍcosθ (1-8)设θ=π+ɸ，假设ɸ与1（单位是弧度）相比很小，即ɸ＜＜1，则可以进行近似处理：cosθ=−1，sinθ=−ɸ，（dθdt ）2=0。

用u来代表被控对象的输入力F，线性化后的两个运动方程如下：{(I+ml2)ɸ−mglɸ=mlẍ(M+m)ẍ+bẋ−mlɸ=u(1-9)假设初始条件为0，则对式（1-9）进行拉普拉斯变换，可以得到：{(I+ml2)Φ(s)s2−mglΦ(s)=mlX(s)s2(M+m)X(s)s2+bX(s)s−mlΦ(s)s2=U(s) (1-10) 由于输出为角度ɸ，求解方程组的第一个方程，可以得到：X(s)=[(I+ml2)ml −gs2]Φ(s) (1-11)或改写为：Φ(s)X(s)=mls2(I+ml2)s2−mgl(1-12)如果令v=ẍ,则有：Φ(s)V（s）=ml(I+ml2)s2−mgl(1-13)如果将上式代入方程组的第二个方程，可以得到：(M+m)[(I+ml2)ml −gs]Φ(s)s2+b[(I+ml2)ml+gs2]Φ(s)s−mlΦ(s)s2=U(s) (1-14) 整理后可得传递函数：Φ(s) U(s)=mlqs2s4+b(I+ml2)qs3−(M+m)mglqs2−bmglqs(1-15)其中q=[(M+m)(I+ml2)−(ml)2]假设系统状态空间方程为：X=AX+Buy=CX+Du (1-16) 方程组对ẍ,ɸ解代数方程，可以得到解如下：{ẋ=ẋẍ=−(I+ml2)bI(M+m)+Mml2ẋ+m2gl2I(M+m)+Mml2ɸ+(I+ml2)I(M+m)+Mml2uɸ=ɸɸ=−mlbI(M+m)+Mml2ẋ+mgl(M+m)I(M+m)+Mml2ɸ+mlI(M+m)+Mml2u(1-17)整理后可以得到系统状态空间方程：[ẋẍɸɸ]=[01000−(I+ml2)bI(M+m)+Mml2m2gl2I(M+m)+Mml200010−mlbI(M+m)+Mml2mgl(M+m)I(M+m)+Mml20][xẋɸɸ]+[(I+ml2)I(M+m)+Mml2mlI(M+m)+Mml2]uy=[xɸ]=[10000010][xẋɸɸ]+[0]u(1-18)由（1-9）的第一个方程为：(I+ml2)ɸ−mgl ɸ=mlẍ对于质量均匀分布的摆杆可以有：I=13ml2于是可以得到：(13ml2+ml2)ɸ−mgl ɸ=mlẍ化简可以得到：ɸ=3g4l ɸ+34lẍ(1-19)设X={x, ẋ, ɸ , ɸ}，u=ẍ则有：[ẋẍɸɸ]=[010000000001003g4l0][xẋɸɸ]+[134l]uy=[xɸ]=[10000010][xẋɸɸ]+[0]u(1-20)以上公式推理是根据牛顿力学的微分方程验证的。

第六章直线一级倒立摆的实时控制6.1 倒立摆实时控制的原理倒立摆系统是一个不稳定系统，当其摆杆在竖直向上的状态下如果无外界干涉、开环的情况下是绝对不稳定的。

那么，为了使摆杆在竖直向上保持稳定状态，就需要给小车一个平行于轨道的方向的控制力，带动摆杆绕着与小车连接的转轴在竖直平面内摆动，尽量保持摆杆与竖直向上方向的夹角为0。

将控制力作为倒立摆系统的输入，小车的位移和摆杆的角度为采集到的反馈信号，计算机在每一个采样周期中采集来自光电编码器测量的小车与摆杆的实际位置、角度信号，反馈给数据采集卡，再传输给计算机，与期望值进行比较后，通过所设计控制算法得到控制量，最后经数模转换驱动电机，这样小车可以通过左右移动来保持摆杆的平衡，实现倒立摆的实时控制。

所以在这里，直线一级倒立摆系统的实时控制的原理可以简单叙述如下：用一种控制方法对小车的运动做适当的控制，从而使小车上的摆杆倒置稳定。

同时，该控制系统能够通过实时采集小车的位置和摆杆的偏离角度，对外界扰动草成的系统不稳定偏差能够及时的修正，保证直线一级倒立摆系统的恒久稳定[25]。

6.2 倒立摆实时控制软件介绍倒立摆系统的实时控制所使用的软件叫做QUARC。

QUARC是Quanser下一代多功能通用快速控制实时控制软件，可以无缝集成Simulink。

它将传统的设计实现接口工具集扩展到新的高度，允许更多的功能，更具弹性的开发手段，更少的培训时间，同时避免重复的开发工作。

而且QUARC实时控制软件具有一些重要特点[26]：(1)完全支持Simulink的扩展模式，软件包括示波器，浮点示波器，显示，在线参数调节等功能，还可以进行实时的参数标绘，提供了各种数据显示及标绘的选项；(2)软件基于Windows下的图形化操作界面，同时解决了在Windows控制实时性较差的问题；(3)系统灵活可扩展的通信，数据采集和控制系统架构；(4)信号，子系统，示波器均可调试，同时具有模型参考模块可支持编译修改能力，参数修改后的效果立即可视。

直线一级倒立摆控制
直线一级倒立摆系统输入为小车的加速度，输出为倒立摆系统摆杆的角度，被控对象的传递函数为：2()0.02725()0.01021250.26705
s V s s Φ=- 给系统施加脉冲扰动，输出量为摆杆的角度时，系统框图如下：
图 3-4 直线一级倒立摆闭环系统图（脉动干扰）
1) 绘制直线一级倒立摆开环根轨迹图、Bode 图和奈奎斯特图，并判断稳定性。

2）用根轨迹法设计控制器，使得校正后系统的要求如下：
调整时间t (2%) s = 0.5s ；最大超调量 M p ≤ 10%
绘制校正后系统的根轨迹图，并给出阶跃响应曲线。

3）通过改变控制器的极点和零点，得到不同的控制效果
4）用频域响应法设计超前校正控制器G c (s ) ，使得系统的静态位置误差常数为10，相位裕量为50o ，增益裕量等于或大于10 分贝。

给出阶跃响应曲线。

5）设计PID 控制器，并给出控制效果。

直线型⼀阶倒⽴摆1---概念篇⼀、倒⽴摆系统的研究⽬的和意义倒⽴摆控制系统（InvertedPendulumSystem简称IPS）是⼀个复杂的、不稳定的、⾮线性系统，是进⾏控制理论教学及开展各种控制实验的理想实验平台。

倒⽴摆的典型性在于：作为被控对象，它是⼀个⾼阶次、不稳定、多变量、⾮线性、强耦合的复杂被控系统，可以有效地反应出控制中的许多问题。

对倒⽴摆系统的研究能有效的反映控制中的许多典型问题：如⾮线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。

通过对倒⽴摆的控制，⽤来检验新的控制⽅法是否有较强的处理⾮线性和不稳定性问题的能⼒。

同时，其控制⽅法在军⼯、航天、机器⼈和⼀般⼯业过程领域中都有着⼴泛的⽤途，如机器⼈⾏⾛过程中的平衡控制、⽕箭发射中的垂直度控制和卫星飞⾏中的姿态控制等。

倒⽴摆的种类有很多，接其澎式可分为：悬挂式倒⽴摆、旋转式倒⽴摆、环形倒⽴摆和平⾯倒⽴摆；按级数可分为：⼀级、⼆级、三级、四级、多级等；接其运动轨道可分为：⽔平式、倾斜式；按控制电机⼜可分为：单电机和多级电机。

研究倒⽴摆系统具有的挑战意义不仅仅是由于级数的增加⽽产⽣的控制难度，并且由于他的本⾝所具有的复杂性、不稳定性以及⾮线性的特点进⽽不断研究拓展的新的理论⽅法，以应⽤到新的控制对象中，提供更好的实验理论和实验平台。

对于机器⼈的直⽴⾏⾛，航天飞⾏器的飞⾏平稳控制都具有⾮常⼤的意义，不断进⾏理论与⼯业的实践结合，推动科学技术的发展，更加⼴泛的应⽤到经济活动中。

这对于航空航天技术的进步具有⾮常⼤的理论意义和实际意义，具有⾮常⼴阔的研究前景。

⼆、直线型⼀阶倒⽴摆原理倒⽴摆系统⼤致可以分为控制器、运动平台、受控杆三部分。

直线型⼀阶倒⽴摆的控制器可以⽤计算机或者单⽚机实现，运动平台为直线型、受控杆为均匀质量铁杆。

受控杆与运动平台相连。

直线型⼀阶倒⽴摆受控过程如下：状态⼀:系统处于⾃然稳定状态即受控杆⾃然下垂、运动平台速度为零、控制器未⼯作。

一、直线一级倒立摆建模根据自控原理实验书上相关资料，直线一级倒立摆在建模时,一般忽略掉系统中的一些次要因素.例如空气阻力、伺服电机的静摩擦力、系统连接处的松弛程度等，之后可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统，如下图所示：倒立摆系统是典型的机电一体化系统,其机械部分遵循牛顿的力学定律,其电气部分遵守电磁学的基本定理.因此,可以通过机理建模方法得到较为准确的系统数学模型,通过实际测量和实验来获取系统模型参数.无论哪种类型的倒立摆系统,都具有3个特性,即:不确定性、耦合性、开环不稳定性. 直线型倒立摆系统,是由沿直线导轨运动的小车以及一端固定于小车上的匀质长杆组成的系统. 小车可以通过传动装置由交流伺服电机驱动. 小车导轨一般有固定的行程,因而小车的运动范围是受到限制的。

虽然倒立摆的形式和结构各异，但所有的倒立摆都具有以下的特性:1) 非线性倒立摆是一个典型的非线性复杂系统，实际中可以通过线性化得到系统的近似模型，线性化处理后再进行控制。

也可以利用非线性控制理论对其进行控制。

倒立摆的非线性控制正成为一个研究的热点。

2) 不确定性主要是模型误差以及机械传动间隙，各种阻力等，实际控制中一般通过减少各种误差来降低不确定性，如通过施加预紧力减少皮带或齿轮的传动误差，利用滚珠轴承减少摩擦阻力等不确定因素。

3) 耦合性倒立摆的各级摆杆之间，以及和运动模块之间都有很强的耦合关系，在倒立摆的控制中一般都在平衡点附近进行解耦计算，忽略一些次要的耦合量。

4) 开环不稳定性倒立摆的平衡状态只有两个，即在垂直向上的状态和垂直向下的状态，其中垂直向上为绝对不稳定的平衡点，垂直向下为稳定的平衡点。

由于机构的限制，如运动模块行程限制，电机力矩限制等。

为了制造方便和降低成本，倒立摆的结构尺寸和电机功率都尽量要求最小，行程限制对倒立摆的摆起影响尤为突出，容易出现小车的撞边现象。

由此，约束限制直线型一级倒立摆系统的实际控制要求可归结为3点:(1)倒立摆小车控制过程的最大位移量不能超过小车轨道的长度;(2)为保证倒立摆能顺利起立,要求初始偏角小于20°;(3)为保证倒立摆保持倒立的平衡态,要求控制系统响应速度足够快。

直线一级倒立摆数学模型建立及线性化处理直线一级倒立摆系统的组成本系统由水平移动的小台车及由其支撑的单节倒立摆构成。

控制输入量是拖动小台车的直流伺服电机的驱动力，被控制量是摆的偏角和小台车的位移。

系统的构成示意如图1所示。

图1系统示意图应用牛顿力学方法建立系统的数学模型在以上假设的前提下，来分析系统的运动情况。

采用隔离的办法，首先分析倒立摆系统的受力情况。

一、小台车的受力分析设小台车的质量为[]M kg ，[]f N 为由电机提供的x 方向的驱动力，[]w f N 为系统的外部干扰作用力，2[]kg m ξ⋅为小车和轨道的摩擦系数，[/]K Nm s 为电动机动特性影响因数，则根据小车水平方向所受的合力，可得如下方程： ()()w F Mx f f f K x ξ=+--+ （1） 其中[]F f N 表示摆的水平运动对台车的作用力，其方向与驱动力[]f N 的方向相反。

二、摆杆的受力分析以小台车与摆的节点为坐标原点，取坐标系如图1。

那么，摆的运动由水平方向，铅直方向以及旋转方向的运动来构成。

记摆的质心距节点的距离为[]L m , 摆的质量为[]m kg ，摆的偏移角为ϕ，那么摆的质心沿各个运动方向的位移分别为：● 水平方向 sin []x L m ϕ+● 铅直方向 cos []L m ϕ● 旋转方向 []rad ϕ且各个方向的运动方程可以表示为：22[sin ]H d f m x L dtϕ=+ （2） 22[cos ]V d f mg m L dtϕ-= （3） sin cos V H J Lf Lf ϕηϕϕϕ+=- （4）其中[]H f N 和[]V f N 分别表示作用在节点上的沿水平方向和铅直方向的反作用力。

记转动惯量为2/3J mL =，摩擦系数为η，则由(2)和(3) 求得[]H f N 和[]V f N ，并代入(4)，得2()cos sin J mL mL x mLg ϕϕηϕϕ++=-+ （5）由于摆的水平方向的推力F f 等于摆的水平运动作用在台车上的阻力H f , 即F H f f = （6）将（2）式中的H f 代入（1）式，得到小台车的运动方程为：2()()(cos )(sin )()w M m x K x mL mL f f ξϕϕϕϕ++++-=+ （7）由（5）式和（7）式可得出倒立摆系统的数学模型为如下方程组：22()()(cos )(sin )()()cos sin w M m x K x mL mL f f J mL mL x mLg ξϕϕϕϕϕϕηϕϕ⎧++++-=+⎪⎨++=-+⎪⎩ （8）直线一级倒立摆系统的结构参数台车的质量(M ) 0.445[kg ]摆的质量(m)0.210[kg]重力加速度(g) 9.8[2m s]/质心距节点的距离(L) 0.305[m]台车与轨道的摩擦系数（ξ） 0.925 2⋅[]kg m摆节点处的摩擦系数（η） 0.06[//]N rad s 电动机动特性影响因数（K） 7.877[/]Nm s。