直线一级倒立摆---开题报告-范例

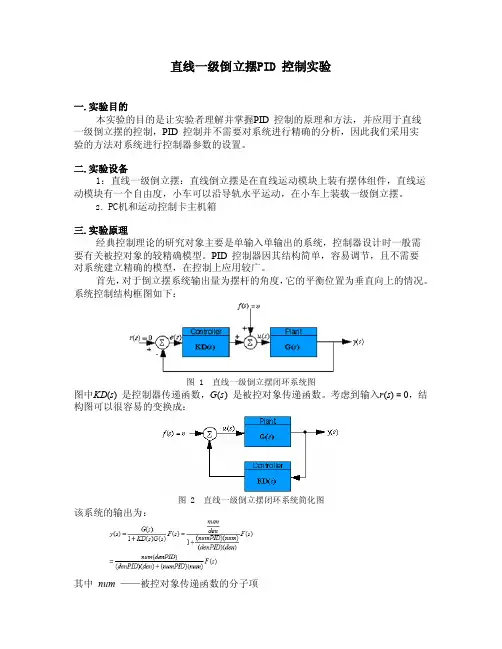
直线一级倒立摆PID 控制实验一.实验目的本实验的目的是让实验者理解并掌握PID 控制的原理和方法，并应用于直线一级倒立摆的控制，PID 控制并不需要对系统进行精确的分析，因此我们采用实验的方法对系统进行控制器参数的设置。

二.实验设备1：直线一级倒立摆：直线倒立摆是在直线运动模块上装有摆体组件，直线运动模块有一个自由度，小车可以沿导轨水平运动，在小车上装载一级倒立摆。

2．PC机和运动控制卡主机箱三.实验原理经典控制理论的研究对象主要是单输入单输出的系统，控制器设计时一般需要有关被控对象的较精确模型。

PID 控制器因其结构简单，容易调节，且不需要对系统建立精确的模型，在控制上应用较广。

首先，对于倒立摆系统输出量为摆杆的角度，它的平衡位置为垂直向上的情况。

系统控制结构框图如下：图 1 直线一级倒立摆闭环系统图图中KD(s) 是控制器传递函数，G(s) 是被控对象传递函数。

考虑到输入r(s) = 0，结构图可以很容易的变换成：图 2 直线一级倒立摆闭环系统简化图该系统的输出为：其中num ——被控对象传递函数的分子项den ——被控对象传递函数的分母项numPID ——PID 控制器传递函数的分子项denPID ——PID 控制器传递函数的分母项通过分析上式就可以得到系统的各项性能。

由(3-13)可以得到摆杆角度和小车加速度的传递函数：PID 控制器的传递函数为：需仔细调节PID 控制器的参数，以得到满意的控制效果。

在控制的过程中，小车位置输出为：通过对控制量v 双重积分即可以得到小车位置。

四.仿真步骤及结果图 3 直线一级倒立摆PID 控制MATLAB 仿真模型其中PID Controller 为封装（Mask ）后的PID 控制器，双击模块打开参数设置窗口 先设置PID 控制器为P 控制器，令0,0,===kd ki kp ，得到以下仿真结果图4从图4中可以看出，闭环控制系统持续振荡，周期约为0.7s 。

倒立摆开题报告范文论文应符合专业培养目标和教学要求，以学生所学专业课的内容为主，不应脱离专业范围，要有一定的综合性，以下就是由编辑老师为您提供的倒立摆开题报告。

一、毕业设计(论文)内容及研究意义(价值)在控制理论发展的过程中，一种理论的正确性及在实际应用中的可行性，往往需要一个典型对象来验证，并比较各种控制理论之间的优劣，倒立摆系统就是这样一个可以将理论应用于实际的理想实验平台。

本论文在参考大量文献的基础上，建立了一级倒立摆系统的数学模型，对系统进行了稳定性、可控性分析，指出一阶倒立摆的开环不稳定性。

文章主要完成了：一级倒立摆动力学模型和模糊PID控制器模块的设计，确定了输入输出信号的论域、隶属度函数和模糊规则，最后利用Matlab中的simulink工具箱创建了基于模糊控制理论的一级倒立摆系统的simulink仿真模型，对倒立摆系统进行分析。

仿真结果证明模糊PID控制不仅可以稳定倒立摆系统，还使小车稳定在平衡位置附近，证明了本文设计的模糊PID控制器有良好的稳定性、鲁棒性和适应性倒立摆系统能有效地反映诸如镇定性、鲁棒性、随动性等许多控制中的关键问题，是检验各种控制理论的理想模型。

其典型性在于：作为实验装置，它本身具有成本低廉、结构简单、物理参数和结构易于调整、便于模拟、形象直观的优点;作为被控对象，它是一个具有高阶次、不稳定、多变量、非线性和强藕合特性的不稳定系统，可以有效地反映控制中的许多问题;作为检测模型，该系统的特点与机器人、飞行器、起重机稳钩装置等的控制有很大的相似性。

对倒立摆因此对倒立摆控制机理的研究具有非常重要的理论和实践意义。

二、毕业设计(论文)研究现状和发展趋势(文献综述)1.倒立摆系统的研究现状到目前为止，人们己经利用包括经典控制理论、现代控制理论以及各种智能控制理论在内的各种手段先后实现了倒立摆系统的稳定控制。

随着微型计算机的发展和广泛应用，又陆续出现了对一级、二级甚至多级倒立摆的稳定控制。

专 业 实 验 报 告 实验名称倒立摆实验 实验时间 姓名 学号一、实验内容1、直线一级倒立摆建模1.1 受力分析针对直线一级倒立摆，在实际的模型建立过程中，可忽略空气流动阻力和其它次要的摩擦阻力，则倒立摆系统抽象成小车和匀质刚性杆组成的系统，如图所示。

图1 小车系统各参数定义：M ：小车质量m ：摆杆质量β：小车摩擦系数l: 摆杆转动轴心到杆质心的长度I ：摆杆惯量F ：加在小车上的力X ：小车位置Ф：摆杆与垂直向上方向的夹角θ：摆杆与垂直向下方向的夹角摆杆受力和力矩分析图2 摆杆系统摆杆水平方向受力为：H摆杆竖直方向受力为：V由摆杆力矩平衡得方程：cos sin Hl Vl I φφθθπφθφ⎧-=⎪=-⎨⎪=-⎩&&&&&& （1） 代入V 、H ，得到摆杆运动方程。

当0φ→时，cos 1θ=，sin φθ=-，线性化运动方程：1.2 传递函数模型以小车加速度为输入、摆杆角度为输出，令，进行拉普拉斯变换得到传递函数：22()()mlG sml I s mgl=+-（2）倒立摆系统参数值：M=1.096 % 小车质量，kgm=0.109 % 摆杆质量，kg0.1β=% 小车摩擦系数g=9.8 % 重力加速度，l=0.25 % 摆杆转动轴心到杆质心的长度，mI= 0.0034 % 摆杆转动惯量，以小车加速度为输入、摆杆角度为输出时，倒立摆系统的传递函数模型为：20.02725()0.01021250.26705G ss=-（3）1.3 倒立摆系统状态空间模型以小车加速度为输入，摆杆角度、小车位移为输出，选取状态变量：(,,,)x x xθθ=&&（4）由2()I ml mgl mlxθθ+-=&&&&得出状态空间模型01001000000013300044xxxxxgglμθθθθ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥'==+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦&&&&&&&&（5）μθθθ'⎥⎦⎤⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=11&&xxxy（6）由倒立摆的参数计算出其状态空间模型表达式：（7）111()()n n n n f s sI A BK s a s a s a --=--=++++L （11）设期望特征根为***12,,,n λλλL ，则期望特征多项式为：***1111()()()n n n n n f x s s s b s b s b λλ--=--=++++L L （12）由*()()f s f s =求得矩阵K 。

直线一级倒立摆系统实验报告1. 实验目的：通过对直线一级倒立摆系统进行分析，掌握系统的基本原理、参数设置和控制策略；提高学生实际动手能力和科学实验能力。

2. 实验内容：（1）搭建直线一级倒立摆系统实验平台；（2）设置系统的动力学模型，采集系统的状态变量；（3）根据系统的特性设计控制策略，实现系统的稳定控制；（4）记录实验数据，并进行数据处理和分析。

3. 实验原理：直线一级倒立摆系统是一种经典的非线性控制系统，其原理和稳定性分析可以使用动力学建模方法来描述。

系统由直线弹簧、质量块、直线导轨和质量块的摆杆组成。

当摆杆处于垂直状态时，系统处于平衡状态；当摆杆被扰动后，系统进入不稳定状态，需要通过控制策略来实现其稳定控制。

在实验中，我们选取了单摆系统作为直线一级倒立摆系统的原形。

单摆系统由一个质点和一个线性弹簧组成，其状态变量为质点的位置和速度。

当质点处于平衡位置时，系统拥有稳定状态；当质点被扰动后，系统进入不稳定状态，需要通过控制策略来实现其稳定控制。

因此，我们可以使用单摆系统来研究直线一级倒立摆系统的控制策略。

4. 实验步骤：（1）搭建实验平台：搭建直线一级倒立摆系统实验平台，包括直线导轨、摆杆、质点、力传感器、位移传感器和控制电路等。

将质点放置在导轨上，并用摆杆将其固定在弹簧上。

使用力传感器和位移传感器来测量系统的状态变量。

（2）设置系统模型：对实验平台的动力学模型进行建模，将系统的状态变量与控制策略联系起来。

（3）设计控制策略：根据系统的特性设计相应的控制策略，使系统保持稳定状态。

常用的控制策略包括模型预测控制、PID控制、滑模控制等。

（4）记录实验数据：实验过程中需要记录系统的状态变量和控制参数，并进行数据处理和分析，得到实验结论。

5. 实验结果分析：通过对直线一级倒立摆系统的实验研究，我们发现系统的稳定控制需要根据其特性和实际情况来确定相应的控制策略。

在实验中，我们采用了模型预测控制策略，通过对系统的状态变量进行预测和调节，成功实现了系统的稳定控制。

倒立摆系统稳摆控制算法研究的开题报告一、研究背景和意义倒立摆是一种经典的非线性、强耦合的动态系统，具有复杂的非线性动力学行为，因此受到了大量研究人员的关注。

倒立摆广泛应用于机器人控制、自动化控制、电子工程等领域，特别是在反馈控制、机器人控制、运动稳定、姿态控制、非线性控制等领域中发挥着重要的作用。

针对倒立摆系统的稳定控制算法研究是经典非线性控制理论的热点和难点问题，具有很高的理论研究和实际应用价值。

二、研究内容和研究方法本文将对倒立摆系统的稳定控制算法进行研究。

具体包括以下几个方面：1. 倒立摆系统建模：倒立摆系统的建模是研究控制算法的基础，本文将基于力学原理，采用数学建模方法对倒立摆系统进行建模，得到其数学模型。

2. 倒立摆系统控制策略研究：本文将采用研究者近几年发展起来的基于三阶计数的自适应 back-stepping 控制策略，结合非线性观测器进行倒立摆系统的控制。

3. 倒立摆系统控制算法仿真实验：本文将采用MATLAB/Simulink 对倒立摆系统控制算法进行仿真实验，验证所提出算法的控制性能。

三、预期研究成果和意义本文的研究成果和意义主要体现在以下几个方面：1. 提出基于三阶计数的自适应 back-stepping 控制策略，具有普适性和实用性。

2. 实现了对倒立摆系统的控制，控制效果良好，验证了所提出算法的控制性能。

3. 为进一步研究非线性控制提供了一个研究方向，并对后续研究倒立摆控制问题具有较大的参考价值。

四、研究计划和进度安排根据以上研究内容，本文的研究计划和进度安排如下：第一阶段（1-2 个月）：查阅相关文献，深入了解倒立摆系统的建模方法和控制策略。

第二阶段（2-3 个月）：对倒立摆系统进行建模，并提出基于三阶计数的自适应 back-stepping 控制策略。

第三阶段（3-4 个月）：采用 MATLAB/Simulink 对所提出算法进行仿真实验，并进行控制性能评估。

第四阶段（1-2 个月）：总结研究成果，撰写毕业论文。

毕业论文开题报告论文题目：单级倒立摆机电系统建模，仿真与控制（基于能量的建模方法）一课题背景：1 单级倒立摆模型在惯性参考系下的水平面上，倒摆由无质量的轻杆和一定质量的小球组成，轻杆通过转动关节安装在小车上．在不考虑空气阻力、摩擦力，并且忽略杆的质量及其弹性变形的情况下，定义x和 分别表示小车偏离基准点的水平位置(小车位移)和倒摆偏离竖直方向的角度(倒摆摆角)．设小车的质量为，小球的质量为m，杆长为z，小车水平方向的驱动力为n．单级倒立摆系统的物理结构如图1所示．2 倒立摆的发展与研究倒立摆系统是一个典型的非线性、强耦合、多变量和不稳定系统，同时也是一种广泛应用的物理模型，倒立摆控制理论产生的方法和技术在半导体及精密仪器加工、机器人技术、导弹拦截控制系统、航空器对接控制技术等方面有广泛的应用，由于倒立摆系统与火箭飞行以及机器人控制具有很大的相似性，已成为人们研究和验证各种控制理论有效性的实验系统，因此对其进行非线性控制方法研究具有重要的理论和实践意义。

在中外有很多学者对倒立摆系统做过深入研究有基于MATLAB单级倒立摆系统研究，单级倒立摆的逼近逆模型及趋近控制研究等。

对于单级倒立摆系统，目前已有多种控制方法可对其实现稳摆控制。

典型的有线性PID控制、常规PID控制、LQR控制、智能控制，模糊控制等。

早在60年代人们就开始了对倒置系统的研究，1966年Schaefer和Cannon应用Bang一_Bang控制理论，将一个曲轴稳定于倒置位置。

在60年代后期，作为一个典型的不稳定、严重非线性之例，人们提出了倒立摆概念，并用其检验控制方法对不稳定、非线性和快速性系统的处理能力，受到世界各国许多科学家的重视，用不同的控制方法控制不同类型的倒立摆，成为具有挑战性的课题之一。

倒立摆系统的控制目标是使倒立摆这样一个不稳定的被控对象，通过引入适当的控制方式使之成为一个稳定的系统，系统上表现为把摆稳定地竖立在本来不稳定的竖直位置。

一级直线倒立摆极点配置控制实验一、实验目的1.运用经典控制理论控制直线一级倒立摆,包括实际系统模型的建立、根轨迹分析和控制器设计、PID 控制分析等内容。

2.熟悉利用极点配置方法来进行倒立摆实验的原理方法。

3.学习MATLAB工具软件在控制工程中的应用。

3.掌握对实际系统进行建模的方法，熟悉利用MATLAB 对系统模型进行仿真，利用学习的控制理论对系统进行控制器的设计，并对系统进行实际控制实验，对实验结果进行观察和分析，非常直观的感受控制器的控制作用。

二、实验设备计算机及MATLAB相关软件元创兴倒立摆系统的软件元创兴一级直线倒立摆系统,包括运动卡和倒立摆实物倒立摆相关安装工具三、倒立摆系统介绍倒立摆是进行控制理论研究的典型实验平台。

由于倒立摆系统的控制策略和杂技运动员顶杆平衡表演的技巧有异曲同工之处，极富趣味性，而且许多抽象的控制理论概念如系统稳定性、可控性和系统抗干扰能力等等，都可以通过倒立摆系统实验直观的表现出来。

学习自动控制理论的学生通过倒立摆系统实验来验证所学的控制理论和算法，非常的直观、简便，在轻松的实验中对所学课程加深了理解。

倒立摆不仅仅是一种优秀的教学实验仪器，同时也是进行控制理论研究的理想实验平台。

由于倒立摆系统本身所具有的高阶次、不稳定、多变量、非线性和强耦合特性，许多现代控制理论的研究人员一直将它视为典型的研究对象，不断从中发掘出新的控制策略和控制方法，相关的科研成果在航天科技和机器人学方面获得了广阔的应用。

四、倒立摆工作原理和物理模型以及数学模型（简述）1、工作原理：数据采集卡（也称运动控制卡，安装于计算机机箱的PCI插槽上）采集到旋转编码器数据和电机尾部编码器数据，旋转编码器与摆杆同轴，电机与小车通过皮带连接，所以通过计算就可以得到摆杆的角位移以及小车位移，角位移差分得角速度，位移差分可得速度，然后根据自动控制中的各种理论转化的算法计算出控制量。

控制量由计算机通过运动控制卡下发给伺服驱动器，由驱动器实现对电机控制，电机尾部编码器连接到驱动器形成闭环，从而可以实现闭环控制。

直线一级倒立摆系统实验报告西北工业大学姓名：张云虎探测制导与控制技术学号：2013300925 1.实验参数介绍2.根据实验指导书给的受力分析结合newton定律得出动力学方程：分析水平方向的合力有：M=F-f-N （1）分析摆杆水平方向的受力得；N-Fs=m（x+lsinθ) ps：Fs=0即N=m+mlθcosθ-mlθsinθ（2）把（2）带入（1）得到：（M+m）+f+ mlθcosθ-mlθsinθ=F（3）对垂直方向的合力进行分析得到：-P+mg+Fh=m(l-lcosθ) ps:Fh=0即P-mg= mlθsinθ+mlθcosθ（4）力矩平衡方程：Plsinθ+Nlcosθ+Iθ=0 （5）把公式（2）（4）带进（5）得到：（I+m）θ+mglsinθ=-ml（6）近似化处理得到：(I+m)ф-mglф=ml(M+m)+f-mlф=u写出状态空间模型：=Ax+Buy=Cx+Du==+ф+ uф=фф= +ф+ u写成矩阵形式，带入参数化简如下：фф =ф= uy= ф = фф+ u3.MATLAB分析：>> A=[0 1 0 0;0 0 0 0;0 0 0 1;0 0 29.4 0]A =0 1.0000 0 0 0 0 0 0 0 0 0 1.0000 0 0 29.4000 0>> B=[0;1;0;3]B =13>> C1=[1 0 0 0]C1 =1 0 0 0>> C2=[0 0 1 0]C2 =0 0 1 0>> C=[C1;C2]C =1 0 0 00 0 1 0>> D=[0;0]D =D1 =>> D2=[0]D2 =状态空间模型如下：>> sys1=ss(A,B,C,D)sys1 =a =x1 x2 x3 x4x1 0 1 0 0x2 0 0 0 0x3 0 0 0 1x4 0 0 29.4 0b =u1x1 0x2 1x3 0x4 3c =x1 x2 x3 x4y1 1 0 0 0y2 0 0 1 0d =u1y1 0y2 0Continuous-time state-space model.4.利用MATLAB判断系统的能控性与观性：>> Qc=ctrb(A,B);>> Qo1=obsv(A,C1);>> Qo2=obsv(A,C2);>> rank(Qc)ans =4>> rank(Qo1)ans =2>> rank(Qo2)ans =2>> rank(obsv(A,C))ans =4因为rank(ctrb（A.B）)=4,所以系统可控；因为rank（obsv(A,C1)）=2,所以输出1不可观测；因为rank（obsv(A,C2)）=2,所以输出2不可观测；因为rank（obsv（A，C）=4，所以由全部输出是可观测的。

倒立摆系统的智能控制研究的开题报告
一、选题背景
倒立摆系统是一种具有非线性、高度敏感、动态不稳定等特点的控制系统，具有广泛的应用领域，在机器人控制、智能控制、自适应控制等领域都有着重要的应用。

然而，传统的控制方法难以应对其高度复杂的动态特性，如何提高控制系统的稳定性和鲁棒性是解决该问题的关键所在。

本文将研究利用智能控制方法对倒立摆系统进行控制，以提高控制系统的稳定性和鲁棒性，并验证其控制效果。

二、研究内容
1.分析倒立摆系统的动态特性，建立倒立摆系统的控制模型，并对其特点进行分析。

2.利用智能控制方法设计倒立摆系统控制器。

具体来说，采用模糊控制、神经网络控制、深度强化学习等智能控制策略，针对倒立摆系统的动态特性进行优化，提高控制器的稳定性和鲁棒性。

3.搭建实验平台，进行仿真和实验验证。

通过模拟实验验证不同智能控制策略对倒立摆系统的控制效果，同时利用实验平台进行实际实验验证，对实验结果进行分析和解释。

三、研究意义
本文将通过对倒立摆系统的智能控制研究，旨在提高控制系统的稳定性和鲁棒性，具有以下研究意义：
1.对倒立摆系统的控制方法进行研究和探索，加深对智能控制技术的理解和应用。

2.提高倒立摆系统的控制效果，为实际应用提供有力支撑。

3.促进控制领域的发展，扩展控制技术的应用范围。

四、预期成果
1.建立倒立摆系统的控制模型，分析其动态特性。

2.设计出基于智能控制方法的倒立摆控制器。

3.通过仿真实验和实际实验对控制器进行验证和分析，得出相应的实验结果和结论。

4.撰写论文，对本文研究内容进行总结和归纳，提出可能的改进方案和研究展望。